求解非线性互补问题基于模的矩阵分裂算法

马昌凤，王 婷

(福建师范大学, 数学与信息学院, 福建 福州, 350117)

求解非线性互补问题基于模的矩阵分裂算法

马昌凤，王 婷

(福建师范大学, 数学与信息学院, 福建 福州, 350117)

建立了一个求解非线性互补问题基于模的矩阵分裂迭代算法, 并在一定条件下分析了该算法的收敛性； 同时通过实验验证了该算法在求解一类弱非线性互补问题时的有效性。

非线性互补问题；基于模的矩阵分裂； 迭代算法； 收敛性分析； 数值实验

考虑如下一类弱非线性互补问题[1,2]: 求解u∈Rn，使得下式成立

u≥0,v=Au+Ψ(u)≥0,uTv=0,

(1)

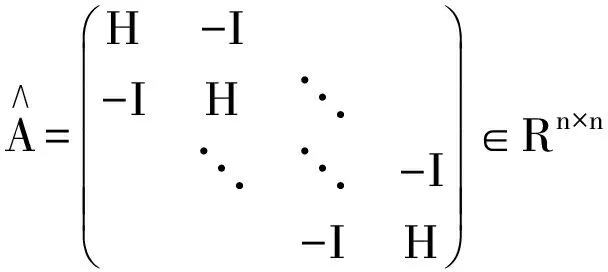
其中,A=(aij)∈Rn×n是给定的大型稀疏矩阵,Ψ(u):Rn→Rn是利普希茨连续非线性函数, 记号“≥”表示两个向量对应的各个分量的大于关系。

在文献[3]中Huang和Ma提出了一种基于模的矩阵分裂方法来求解非线性互补问题:(Ω+M)xk+1=Nxk+(Ω-A)|xk|-γΨ(uk),

(2)

在文献[4]中,Li提出了一种广义的基于模矩阵分裂方法来求解线性互补问题:(Ω2+MΩ1)xk+1=NΩ1xk+(Ω2-AΩ1)|xk|-q,

(3)

并且, 令uk+1=Ω1(|xk+1|+xk+1)。这里Ω1，Ω2是两个正对角矩阵，q是常向量。

结合这两种方法, 本文提出一种新的基于模的矩阵分裂方法来求解非线性互补问题(1)。

1 一个基于模的矩阵分裂迭代算法

定理1 假设AΩ1=MΩ1-NΩ1是矩阵AΩ1的一个分裂,Ω1,Ω2∈Rn×n是两个正对角矩阵。 则下面结论成立:

(4)

(2)如果x满足不动点方程(4),则

(5)

是非线性互补问题(1) 的一个解。

再利用分解AΩ1=MΩ1-NΩ1, 便有

因此, (1) 得证。

现在来证明(2)。通过一些简单的计算, 可发现不动点方程与下式等价:

容易得到u≥0,v≥0，uTv=0和v=Au+Ψ(u)， 也就是说, (u,v) 是互补问题的一个解。因此,(2) 成立。

基于定理1, 现提出如下广义的基于模分裂算法:

(6)

(7)

假设AΩ1=D-L-U,其中D,L,U分别是矩阵AΩ1的对角, 严格下三角和严格上三角矩阵。当对矩阵AΩ1进行不同的分裂时, 由式子(6)可以构造出一系列的基于模的矩阵分裂迭代方法。

例如, 当选取MΩ1=D，NΩ1=L+U时, 可以产生如下广义的基于模的Jacobi(GMJ)迭代方法

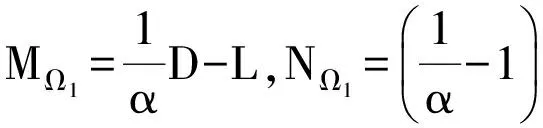
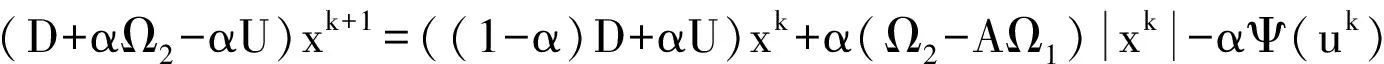
当α=1时, 上式就退化成广义的基于模的Gauss-Seidel(GMGS)迭代方法。

2 收敛性分析

在本节中, 我们建立了当矩阵AΩ1是正定矩阵时的收敛理论。

定理2 假设AΩ1∈Rn×n是一个正定矩阵,AΩ1=MΩ1-NΩ1是矩阵AΩ1的一个分裂, 其中MΩ1∈Rn×n是正定的。假设Ω2∈Rn×n是一个正对角矩阵,γ是一个正常数,

Ψ(u):Rn→Rn是利普希茨连续函数,L是利普希茨连续常数, 也就是, 对于任意的u1,u2∈Rn，都有‖Ψ(u1)-Ψ(u2)‖≤

L‖u1-u2‖成立, 定义

f(Ω1,Ω2)=‖(Ω2+MΩ1)-1(Ω2-MΩ1)‖，

g(Ω1,Ω2)=‖(Ω2+MΩ1)-1NΩ1‖+

L‖Ω1‖‖(Ω2+MΩ1)-1‖，

其中, ‖·‖是任意一种矩阵范数, 并且令ρ(Ω1,Ω2)=f(Ω1,Ω2)+2g(Ω1,Ω2)

(8)

结合式(6) 我们得到

(Ω2+MΩ1)(xk+1-x*)=

注意到,Ω2和MΩ1都是正定矩阵, 这意味着Ω2+MΩ1也是正定的, 所以，Ω2+MΩ1是非奇异的。 结合上式和AΩ1=MΩ1-NΩ1可得

xk+1-x*=

(Ω2+MΩ1)-1NΩ1(xk-x*)+

(Ω2+MΩ1)-1(Ψ(uk)-Ψ(u*))=

(Ω2+MΩ1)-1NΩ1(xk-x*)+

(Ω2+MΩ1)-1(Ψ(uk)-Ψ(u*))=

(Ω2+MΩ1)-1NΩ1(xk-x*)+

(Ω2+MΩ1)-1(Ψ(uk)-Ψ(u*)),

根据上式可得,

‖xk+1-x*‖≤

‖(Ω2+MΩ1)-1‖‖(Ψ(uk)-Ψ(u*))‖≤

2‖(Ω2+MΩ1)-1NΩ1‖‖xk-x*‖+

‖(Ω2+MΩ1)-1(Ω2-MΩ1)‖‖xk-x*‖+

L‖(Ω2+MΩ1)-1‖‖uk-u*‖，

其中, 最后一个不等式成立是由于Ψ(u)是利普希茨连续函数,L是利普希茨常数。

另外有

因此, 我们可以得到

‖xk+1-x*‖≤

2‖(Ω2+MΩ1)-1NΩ1‖‖xk-x*‖+

‖(Ω2+MΩ1)-1(Ω2-MΩ1)‖‖xk-x*‖+

2L‖Ω1‖‖(Ω2+MΩ1)-1‖‖xk-x*‖=

{2(‖(Ω2+MΩ1)-1NΩ1‖+

L‖Ω1‖‖(Ω2+MΩ1)-1‖)+

‖(Ω2+MΩ1)-1(Ω2-MΩ1)‖}‖xk-x*‖=

(f(Ω1,Ω2)+2g(Ω1,Ω2))‖xk-x*‖。

特别地, 当MΩ1∈Rn×n是对称正定矩阵,Ω2=ωI∈Rn×n是正数量矩阵时(这里ω是某个正常数), 下面将给出这种情况下的收敛定理。为了讨论方便, 我们引入一些参数记号：

θ(τ)=

其中,λmin，λmax分别是矩阵MΩ1的最小和最大特征值,L是函数Ψ(u) 的利普希茨常数。有了这些记号, 就可给出下面的收敛理论：

证明 由定理2知, 只需要得到保证ρ(Ω)<1的条件. 利用谱半径的性质和MΩ1是对称正定矩阵,τ≥0可得,

‖(Ω2+MΩ1)-1NΩ1‖2=

‖(Ω2+MΩ1)-1‖2=‖(ωI+MΩ1)-1‖2=

‖(Ω2+MΩ1)-1(Ω2-MΩ1)‖2=

‖(ωI+MΩ1)-1(ωI-MΩ1)‖2=

因此我们得到,

ρ(Ω1,Ω2)=f(Ω1,Ω2)+2g(Ω1,Ω2)=

‖(Ω2+MΩ1)-1(Ω2-MΩ1)‖2+

2‖(Ω2+MΩ1)-1NΩ1‖2+

2L‖(Ω2+MΩ1)-1‖2‖Ω1‖2=

ρ(Ω1,Ω2)=

ρ(Ω1,Ω2)=

化简得,ω2-(τλmax+Lσ-λmin)ω-λmax(τλmin+Lσ)>0，

(9)

化简得,

(τλmax+Lσ-λmin)ω+Lσλmax+

(τ-1)λminλmax<0，

(10)

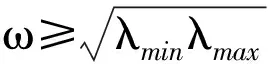
3 数值实验

本节将用两个数值例子来证实所提方法求解NCP(1) 的可行性和有效性。所有的实验都是在MATLAB2010b上实现的, 操作系统是Win7。我们从解决问题所耗的CPU时间(秒)(记为‘CPU’)、所需要的迭代次数(记为‘IT’)还有残差向量范数 (记为‘RES’) 三个方面来比较测试方法。在实际操作中, 选取初始值x(0)=(1,0,1,0,…)T。终止条件是当前步残差满足RES≤10-5或者达到最大迭代步数kmax=1000, 其中RES定义如下:

RES=‖min(Au(k)+Ψ(u(k)),u(k))‖2。

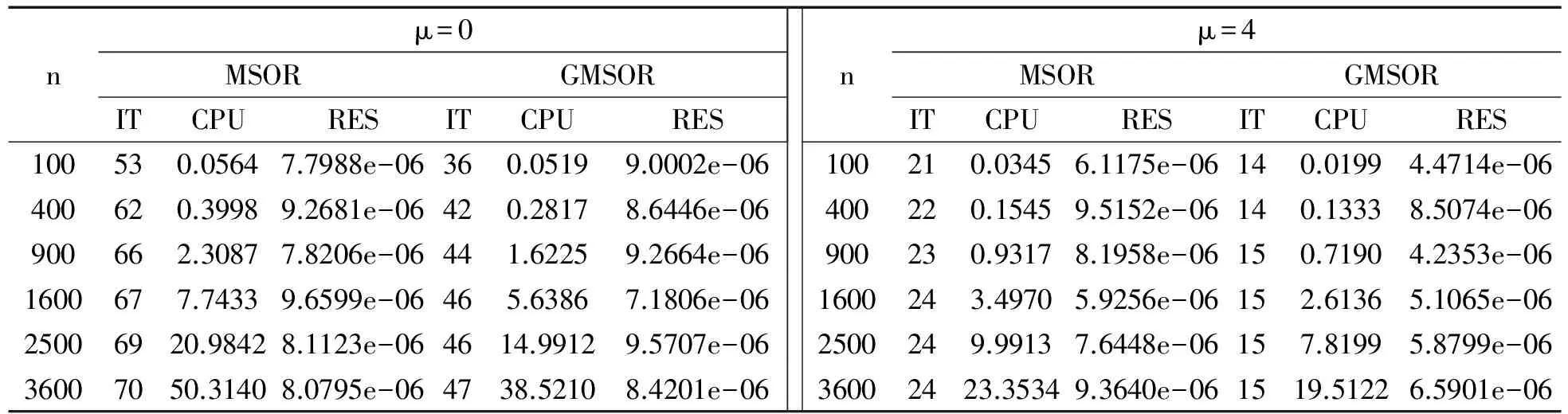
表1 例1的数值结果

表2 例2的数值结果

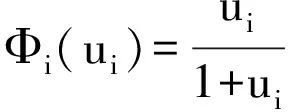
Φi(ui),(这里i=1,2,…,n)

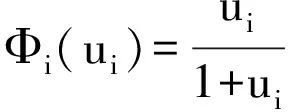
4 小结

从表1和表2可以看出, 不管是μ=0还是μ=4这两种情况, GMSOR 方法的迭代步与时间都是少于MSOR 方法的, 这说明了GMSOR方法在处理这类弱非线性互补问题是更有效的。所以, GMSOR方法不管是处理线性互补问题还是非线性互补问题都是可取的, 我们将它推广到非线性互补问题上是有意义的。但是, 对于方法中的参数α,t, 如何选取最优参数使得收敛效果达到最好, 还需要进一步研究。

[1]韩继业, 修乃华, 戚厚铎.非线性互补问题理论与算法[M]. 上海:上海科学技术出版社, 2006.

[2]PANG J S. On the convergence of a basic iterative method for the implicit complementarityproblems[J]. Journal of Optimization Theory and Applications, 1982, 37(2):149-162.

[3]HUANG N, MA C F.The modulus-based matrix splitting algorithms for a class of weakly nonlinear complementerity problems[J]. Numerical Linear Algebra with Applications, 2016,23:558-569.

[4]LI W.A general modulus-based matrix splitting method for linear complementerity problems of H-matrices[J].Applied Mathematics Letters,2013,26:1159-1164.

[5]XIA Z C, LI C L. Modulus-based matrix splitting iteration methods for a class of nonlinear complementerity problem[J]. Applied Mathematics and Computation, 2015, 271:34-42.

A modulus-based matrix splitting algorithm for nonlinear complementarity problems

MA Changfeng，WANG Ting

(College of Mathematics and Informations, Fujian Normal University,Fuzhou 350007,China)

A general modulus-based matrix splitting iteration method is proposed for solving nonlinear complementarity problems. And the convergence of the proposed method is analyzed. Finally, some numerical results are reported to show the effectiveness of the algorithm.

nonlinear complementarity problems; modulus-based matrix splitting; iteration method; convergence analysis; numerical experiment

2017-05-28

中国科学院战略性先导科技专项(XDB18010202); 福建省自然科学基金项目(2016J01005)

马昌凤(1962-), 男，湖南隆回人,教授, 博士,博士生导师, 从事偏微分方程数值解与数值代数及其应用研究

1672-7010(2017)04-0001-06

O241.7

A