无人驾驶汽车横向滑模控制仿真研究
2017-08-24肖旭辉魏敬东LiuWeiXiaoXuhuiWeiJingdong
刘 伟,肖旭辉,魏敬东 Liu Wei,Xiao Xuhui,Wei Jingdong
无人驾驶汽车横向滑模控制仿真研究
刘 伟,肖旭辉,魏敬东 Liu Wei,Xiao Xuhui,Wei Jingdong
(长安大学汽车学院,陕西 西安 710064)
使用2自由度车辆模型将基于视觉预瞄的无人驾驶汽车横向运动模型简化。对简化后的模型,引入滑模控制的方法,通过控制输入量(前轮转角)使预瞄点处的航向偏差和横向距离偏差最小。同时考虑到滑模控制存在的抖振现象会影响整个控制的稳定性,使用具有连续变化特性的双曲正切函数代替符号函数。最后通过CarSim和Simulink联合仿真验证方法的可行性。
无人驾驶汽车;滑模控制;双曲正切函数;CarSim;Simulink
0 引 言
无人驾驶汽车的运动控制技术是无人驾驶汽车技术中一项重要的内容。其中横向控制是指在跟踪待执行路径时,控制车辆与待执行路径之间的距离偏差等变量趋于零。关于横向运动控制的方法,有很多文献对此加以研究,如经典的PID(Proportion,Integral,Derivative,比例、积分、微分)控制、最优控制[1]、鲁棒控制[2]、自适应控制、模型预测控制[3]以及模糊控制等。
引入滑模控制的方法,对车辆运动学模型设计控制器,考虑到抖振抑制的问题,通过仿真平台进行验证。仿真结果表明,所设计的方法能将偏差控制在可接受的范围内,且对干扰具有一定的抑制能力。
1 车辆视觉预瞄运动模型
视觉导航车辆使用传感器测得预瞄点处的横向偏差和航向偏差,通过控制算法计算出前轮转角的变化量,根据前轮转角转动转向盘,实现对路径的精确跟踪。车辆预瞄运动学模型如图1所示[4]。
图1的模型可表示为
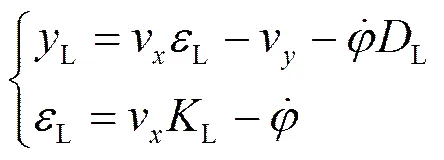
式中,L为预瞄点处与待执行路径的横向偏差,m;L为车辆预瞄点处和路径切线行成的航向偏差,rad;v为车辆质心处的纵向车速,km/h;v为车辆质心处的横向车速,km/h;为车辆的横摆角,rad;为车辆的横摆角速度,rad/s;L为待执行路径的曲率;L为预瞄距离,m。
2 车辆2自由度模型
根据经典的汽车操稳性理论,汽车可以简化为具有侧向及横摆运动的2自由度模型,如图2所示[5]。
由图2可以得出
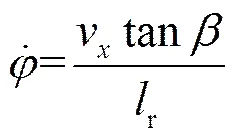
(3)
(4)
图2中,g为质心,为车辆质心侧偏角;r为质心距后轴的距离,m;f为质心距前轴距离,m;f为前轮转角。
将车辆2自由度模型和车辆预瞄运动学模型结合,得到无人驾驶汽车控制方程为

3 横向偏差与航向偏差的确定
在实车运行时偏差量由摄像头采集路面信息和计算机计算获得,采用仿真软件CarSim可以直接输出预瞄点处的横向偏差L。航向偏差L可由车辆预瞄点A和A点在路径上的对应点B的坐标求得。
CarSim软件可以输出这两个点的坐标。假设0时刻A点的坐标为A(x0,y0),经过一个仿真步长到达1,此时对应的点为A′(x1,y1);同理,0时刻B点的坐标为B(x0,y0),1时刻为B′(x1,y1)。
则航向偏差为

4 控制器设计
4.1 滑模变结构控制器设计
将无人驾驶汽车控制方程写成矩阵形式为
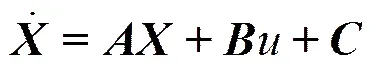
式中,
由于道路曲率L无法测得,所以项可以看作系统的干扰项。仿真所选道路的曲率为有限值,速度v为恒速,设vKL≤1,1为干扰最大值。设计滑模面函数为=,其中为1×2的设计向量,其内元素均大于0,元素的大小影响系统状态在滑模面附近变化的速率,实际使用时常根据经验确定的取值。则滑模面函数的导数为,当系统状态到达滑模面时,,结合上式,忽略掉干扰项,求得此时的等效控制量为
(8)
设切换控制量为
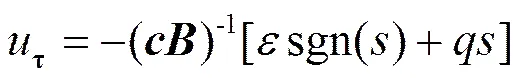
式中>0,>0,二者都为调节系数,和的大小会影响控制量对滑模面变化的敏感度,根据经验确定。则总控制量为等效控制量和切换控制量之和,即
(10)
此时
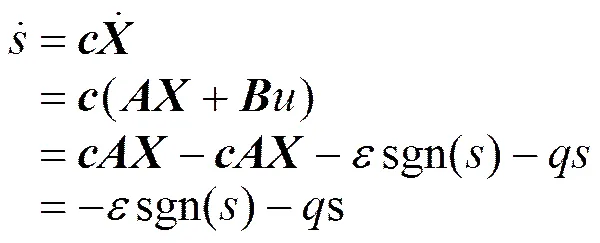
显而易见,能满足滑动模态的可达条件为
(12)
4.2 滑模抖振的抑制
关于抖振的抑制,这里引入双曲正切函数来替换控制量中的开关函数[6]。表示为

式中>0,使用连续光滑的双曲正切函数来代替不连续变化的切换函数,可以有效地降低控制的抖振。此时,控制量变为
(14)
5 仿真分析
5.1 CarSim/Simulink联合仿真平台搭建
基于CarSim/Simulink建立的无人驾驶汽车横向滑模变结构控制联合仿真平台结构如图3所示。
为了实现CarSim/Simulink联合仿真,需要对CarSim输入与输出接口参数进行正确的配置。输入与输出接口参数配置见表1。
5.2 仿真结果分析
为了验证建立的横向滑模控制器的有效性,在建立的联合仿真平台上,对不加消抖函数和使用消抖函数的滑模控制器进行仿真对比分析。
表1 CarSim输入与输出接口参数配置
类别参数名称参数含义 输入参数IMP_STEER_SW转向盘转角 输出参数L_Drv_1预瞄点1处的横向距离偏差 Vx车速 X_RdS_1路径上预瞄点1的横坐标 Y_RdS_1路径上预瞄点1的纵坐标 A_Comp车辆航向角 Lx_Sen_1预瞄距离
仿真试验使用的待跟随路径在全局坐标系下的形状如图4所示,且试验时车辆的起始位置为(0,0),车速v=30 km/h,仿真时间为97 s。仿真开始的前4 s不使用滑模控制器,而是使转向盘向左偏移一定的角度,由图5可以看出这使得横向偏移量达到0.3 m。将上述偏移量视为干扰,接下来接入滑模控制器,检验所设计的滑模控制器抗干扰的能力。SMC1为没有采用消抖函数的滑模控制器,SMC2为采用消抖函数的滑模控制器。由图6可知,二者的横向距离偏差由0.3 m在较短的时间内回落到0 m附近,因此所设计的滑模控制器可以消除干扰,使系统重新回到稳定状态。且由图5和图6可知SMC1和SMC2在横向偏差和航向偏差的控制方面相差不大,都能使偏差保持在可接受的范围内(航向偏差0.03 rad以内,横向偏差0.05 m以内);由图7可知,在对转向盘抖振的抑制方面,SMC2比SMC1效果更好,能使转向盘的抖振下降5°左右。
6 结论与展望
对具有强非线性特性的汽车运动模型进行简化,针对简化模型设计易于实现的控制器。可以得出,设计的横向滑模控制器既有一定的抗干扰能力,又可以使航向偏差和横向距离偏差控制在可接受的范围内,还考虑到对抖振的抑制,对无人驾驶汽车的路径跟踪来说,有一定的合理性。但控制器对干扰抑制的反应有些缓慢。除此之外,如何在试验车速比较高的情况下保证控制的精度,也是需要进一步研究的内容。
[1]刘子龙,杨汝清,杨明,等. 无人驾驶车辆横向位置最优跟踪控制[J]. 上海交通大学学报,2008,42(2):257-265.
[2]宋彦,赵盼,陶翔,等. 基于µ综合的无人驾驶车辆路径跟随串级鲁棒控制方法[J]. 机器人. 2013,35(4):35-42.
[3]Chen B C, Luan B C, Lee K. Design of Lane Keeping System Using Adaptive Model Predictive Control [C]// IEEE International Con- ference on Automation Science and Engineering. IEEE, 2014: 922-926.
[4]郭景华,胡平,李琳辉,等. 基于遗传优化的无人车横向模糊控制[J]. 机械工程学报,2012,48(6):76-82.
[5]Bae I, Moon J, Cha J, et al. Integrated Lateral and Longitudinal Control System for Autonomous Vehicles [C]// IEEE 17th International Conference on Intelligent Transportation Systems. IEEE, 2014: 406-411.
[6]刘金琨. 滑模变结构控制MATLAB仿真:基本理论与设计方法[M]. 北京:清华大学出版社,2015.
2017-04-06
1002-4581(2017)04-0031-04
TP 273
A
10.14175/j.issn.1002-4581.2017.04.009
