基于轴系轨迹的水泵机组振源识别理论初探
2017-08-23李耀辉朱双良
李耀辉,朱双良
基于轴系轨迹的水泵机组振源识别理论初探
李耀辉1,朱双良2
(1. 云南省水利水电投资有限公司,昆明 650051; 2. 云南水投牛栏江滇池补水工程有限公司,昆明 650051)
大型水泵机组的振动其诱因具有多源性,且振动分析主要依靠工程经验,具有一定的不确定性。本文以立式水泵机组电动机转子和水泵转轮形心轨迹运动方程为基础,通过理论推导发现水泵机组可测振动摆度与轴系运动参数之间存在关联。将水泵机组轴系振动的振源分为内部因素和外部因素两类,进而分别建立了内部因素与轴系摆度、外部因素与轴系摆度之间的转移矩阵。根据振源特性和轴系摆度之间的物理分析,提出了以轴系摆度为观测基础的振源识别方法。最后,结合某泵站的实例进行了分析。本文提出的方法揭示了可测轴系摆度参数与系统运动参数之间的内在耦合动力学机制,是对轴系振动分析理论的一种积极的探索和尝试。
水泵机组;电动机;轴系振动;轨迹方程;振源识别;转移矩阵
0 前言
大型水泵机组尺寸大、相对刚度弱,由此引起的振动问题已成为影响大型水泵机组安全稳定运行和提高运行管理水平的关键技术问题[1]。为提高大型泵站的运行管理水平,一些大型泵站已配置以轴系摆度为核心的实时振动监测系统[2-4]。近年来,针对大型水泵轴系的研究逐步增加,如有限元计算方法与转子动力学方法相结合在水泵机组轴系振动分析中可获得更精细的结构振动特性[5,6]、有限元方法与试验测试相结合的研究[7,8],轴系振动信号的提取算法研究[9-11]等。然而,水泵机组涉及的水机电多场耦合问题,随着机组尺寸的加大而被放大,诱发振动的振源具有多源性,振动诊断和分析更趋复杂。因此,从理论上探索轴系振动特征和振源之间的动力学机理,通过轴系振源识别,为振动分析和解决振动问题提供方向性的指导,具有积极的意义。
大型水泵机组大通常具有完整的轴系支撑结构,从其轴系几何结构来看,与水力发电机组轴系几何结构非常相似[12]。因此,水泵轴系振动的研究可借鉴水力发电机组轴系振动的相关研究成果。另一方面,水泵机组由于安装、调试、运行条件等诸多因素的影响,其轴系特性难以进行精确的有限元建模和计算。因此,采用类似于水力发电机组轴系的集中参数建模方法[13],研究水泵机组轴系振动特征仍然是一种有效的方法。
基于上述分析,本文尝试从理论上揭示轴系振动表象与轴系结构特征之间的耦合动力学机制,建立轴系可测摆度与轴系运动参数之间的关联矩阵。利用轴系振动测试数据和轴系运动参数的特性变化,初步识别水泵机组振动的原因。
1 轴系基本模型
立式水泵机组轴系简化为图1所示的二圆盘三支承结构模型。

图1 立式水泵机组轴系结构示意图
图1中,1、1、2、3、2分别为上导轴承、电动机转子、下导轴承、水导轴承及水泵转轮的几何形心。2、2分别是电动机转子、水泵转轮的径向位移,3、4、5分别是机组大轴在上导、下导、水导轴承处的径向位移。
设电动机转子形心坐标为(1,1),其质量偏心为1,电动机转子的径向位移12=(12+12)。设水泵转轮形心坐标为(2,2),其质量偏心为2,水泵转轮的径向位移22=(22+22)。
参照文献[13]的推导,利用经典的拉格朗日方程和振动力学理论,可导出电动机转子和水泵转轮的运动方程如下:

(2)
(3)

关于上述方程有以下几点说明:
(1)设上导、下导、水导轴承支撑刚度系数分别是1、2、3不变,支撑刚度与等效刚度之间的转化关系为
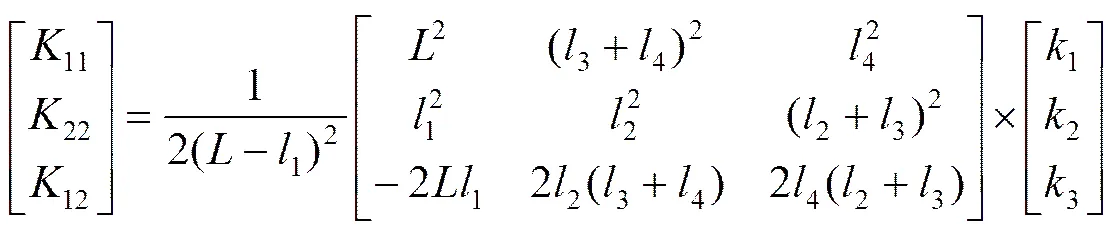
写成矩阵形式:
(6)
其中,=[112212]T,=[123]T。
(2)在泵组转速不变的稳态工况下,电动机转子和水泵转轮形心轨迹具有相似的形态。当角速度为时,电动机转子摆度圆半径与水泵转轮摆度圆半径之比采用该转速下电动机X方向摆度1与水泵转轮X方向摆度2之比来近似,记为:
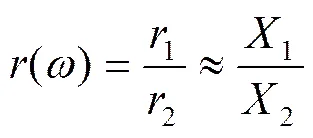
定义上述()的目的是为了实现轴系轨迹振动方程中的耦合刚度项的解耦。由于耦合刚度在刚度项中所占比重较小,因此,()即使有一定误差,对计算结果影响也较小。
(3)根据旋转机械的特点,作用于电动机转子和水泵转轮上的附加外力,尽管形式多样,其基本特性是具有周期性。因此,本文中仅考虑其基频成份,且简化为简谐激励形式。这是轴系轨迹方程求解的前提条件。
由图1的结构来看,若忽略主轴弯曲变形的影响,则三个轴承的摆度与电动机转子和水泵转轮的摆度之间存在确定的几何关系,即:
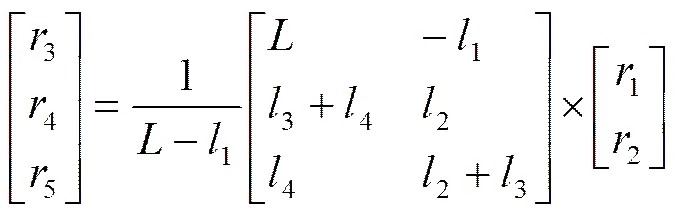
形心轨迹圆半径直接用摆度代替,将上式写成矩阵形式:
(9)
其中,345=[345]T,3、4、5分别是上导、下导、水导轴承摆度,12=[12]T,1、2分别是电动机转子和水泵转轮摆度。
上述k和x是不同参数之间的转移矩阵。
轴系轨迹方程(1)~(4)中包含了轴系运动的主要特征。实际运行中的水泵机组难以对电动机转子和水泵转轮的摆度进行测量,其振动摆度反映在轴系支撑轴承的摆度变化上。工程中也是通过测量支撑轴承摆度来评估水泵轴系振动的。因此,可利用轨迹方程的幅值变化间接获取轴系主要特征参数与轴系振动之间的联系。
2 内部和外部两类振源
假设轴系摆度测量中X方向和Y方向在数值上是一致的。选取公式(1)的幅值作为电动机转子摆度1,公式(3)的幅值作为水泵转轮的摆度2。公式(1)、(3)包含了轴系振动的五个特征参数:固有频率、阻尼比、等效刚度、质量偏心和附加外力。这些因素的变化,通过转移矩阵转化为轴系三个支撑轴承的振动。三个轴系振动幅值大小的不同组合,代表了轴系结构参数不同的变化。
将轴系参数粗略分为外部因素和内部因素两类。
(1)外部因素包括质量偏心和附加外力两个因素。转子和转轮的质量偏心,从形式上来看,相当于形成了一个附加的作用力,因此将其归入外部因素是恰当的。
(2)内部因素包括固有频率和阻尼比两个因素。固有频率与刚度直接相关,阻尼比与阻尼系数直接相关,而刚度和阻尼系数属于振动系统的结构参数,固有频率和阻尼比是振动系统的运动描述参数。因此,从系统结构或运动描述两个角度来看,将其划为内部因素都是恰当的。
按外部因素和内部因素,将摆度方程(1)、(3)分为两部分。内部结构参数,记为:

外部因素记为:
(11)
其中,下标()有两个取值,为(1)表示电动机转子参数,为(2)表示水泵转轮参数。
于是式(1)、(3)的幅值部份,可写为矩阵形式:
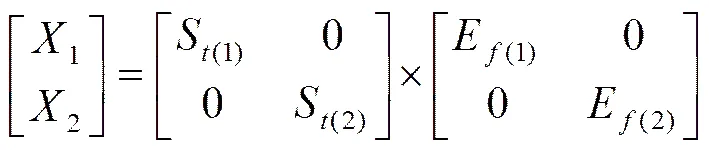
从式(11)的构成形式来看,振动识别需要首先识别振动类型是内部或外部因素引起,然后再进一步分解。
3 振源识别
3.1 外部因素识别
假设轴系振动是由外部因素引起的,其内部结构参数是正常的,即S(i)可视为不变的常数。则式(12)可改写为:
结合式(9)和式(11)、(12),有:
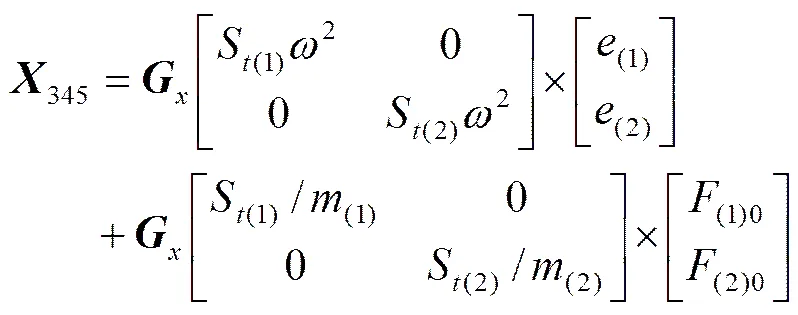
由于变换矩阵x为常数矩阵,式(13)实际上反映了轴系摆度与轴系运动参数(i)和(i)0之间存在明确的对应关系。
由外部因素引起的振动有以下特性:
A. 质量偏心或轴线不正引起的振动会随机组旋转速度增加而增加。
B. 电动机转子中的不平衡磁拉力与励磁电流有关,即不同负荷下的不平衡磁拉力是不同的。
C.水泵转轮中的不平衡力,如水力不平衡等也是与负荷有关。
根据上述基本特性,可给定不同负荷,测试三个轴承摆度变化,即可判断引起振动的外部因素。例如:
A. 若不同负荷下,三个轴承振动摆度不同,则振源来自于不平衡外力,在不平衡外力中,可根据345的变换情况确定是来自电动机或者水泵转轮。
B. 若不同负荷下,三个轴承振动摆度变化较小或不变,则振动诱因是质量偏心或轴线不正。可通过改变水泵转速,根据345各分量的变化,进一步判断质量偏心来自电动机或水泵。在转速变化时,内部因素S(i)()也会有相应的变化。
3.2 内部因素识别
将式(10)改写为如下形式:

根据固有频率角速度表达式结合式(7),式(14)变形为:

(15)
结合式(9)、(12)和(15)式,有:
(16)
通过上述变换,式(16)建立了三个轴承摆度与轴承支撑刚度之间的直接联系。
假设轴系振动是由内部因素引起的,其外部运动参数正常的,即机组在额定转速下运行时可视为常数保持不变。式(16)的关系矩阵中,反映内部结构特性变化的主要是A矩阵,其余矩阵是常数矩阵。同样可根据内部结构特性进行识别。
(1)从A的形式来看,当转速一定时,阻尼比越大,A的数值越小。根据这一特性,可采用泵站两台机组在相同转速下三个轴承摆度为参考,通过对比方法进行识别。
(2)若阻尼比相同,则A与转速相关和固有频率相关,且从刚度关系来看,A的阶次高于刚度k的阶次,A的取值起主导作用。在相同转速下,若固有频率减小、刚度减小,轴系摆度加大。
3.3 振源识别的数值计算方法
公式(13)给出了轴系可测摆度345与轴系运动参数(i)和(i)0之间关联结构;公式(16)给出了轴系可测摆度345与轴系内部结构参数支承刚度之间关联结构。轴系的这种外部可测参数与轴系结构和运动参数之间的关联是通过其几何结构建立的。
基于公式(13)和(16)可进一步开展的工作有以下三方面:
(1)结合内部因素和外部因素对轴系振动影响的特点,可设计多种辨识方法。本文上面提到的辨识方法仅仅是一些直观的讨论。
(2)利用上述关联矩阵,建立数字计算方法,进行更详细的振源识别算法。尤其是对于某一结构形式固定水泵机组,可通过预设振源信号,计算出轴系摆度的各种变化情况,建立振源与摆度变化对照表,为实际泵组的振动分析提供直接的参考。
(3)对于同时包括内部因素和外部因素的多源耦合振动问题。同样可利用公式(16)采用数字计算方法进行计算分析,此时的矩阵不再是常值矩阵。在多源耦合条件下,存在和A两个变化矩阵,其算法设计将更为复杂。
4 实例分析
某泵站运行中,发现2号水泵机组振动幅度明显大于其它机组。因此,在本节的实例计算中,以振动正常的1号水泵机组作为参考,识别振动原因,为下一步的检修调试提供理论支撑。
两台水泵具有相同的结构参数,轴系几何参数1=1.421m,2=1.402m,3=3.700m,4= 1.000m。电动机转子质量1=42400kg,水泵转轮质量2=3362kg。
根据无水启动试验中1号、2号水泵机组摆度测试数据,选择趋势较好的Y方向数据进行计算。两台水泵机组实测转速点不同,因此,采用两个表格分别给出测试数据,见表1、表2。
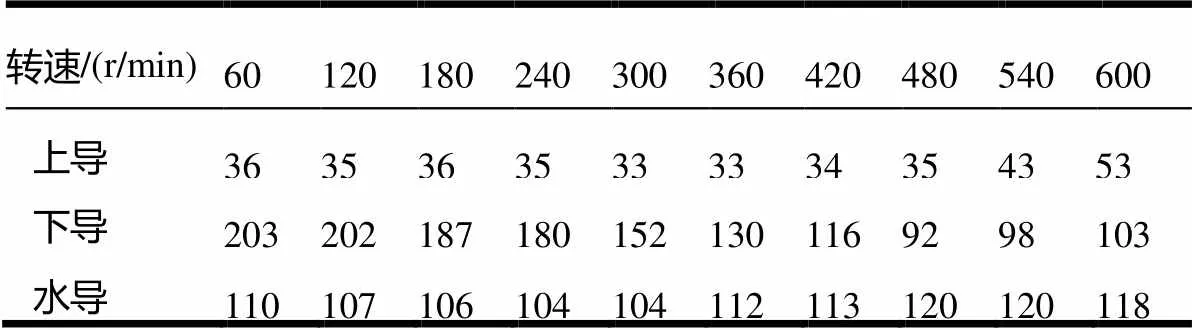
表1 1号泵组无水启动Y方向数据 /μm

表2 2号泵组无水启动Y方向数据 /μm
首先按试验测试得到的三个支撑轴承的摆度数据进行拟合,然后插值计算方法得到电动机转子和水泵转轮的摆度值。两台水泵机组电动机转子和水泵转轮摆度拟合曲线如图2所示。
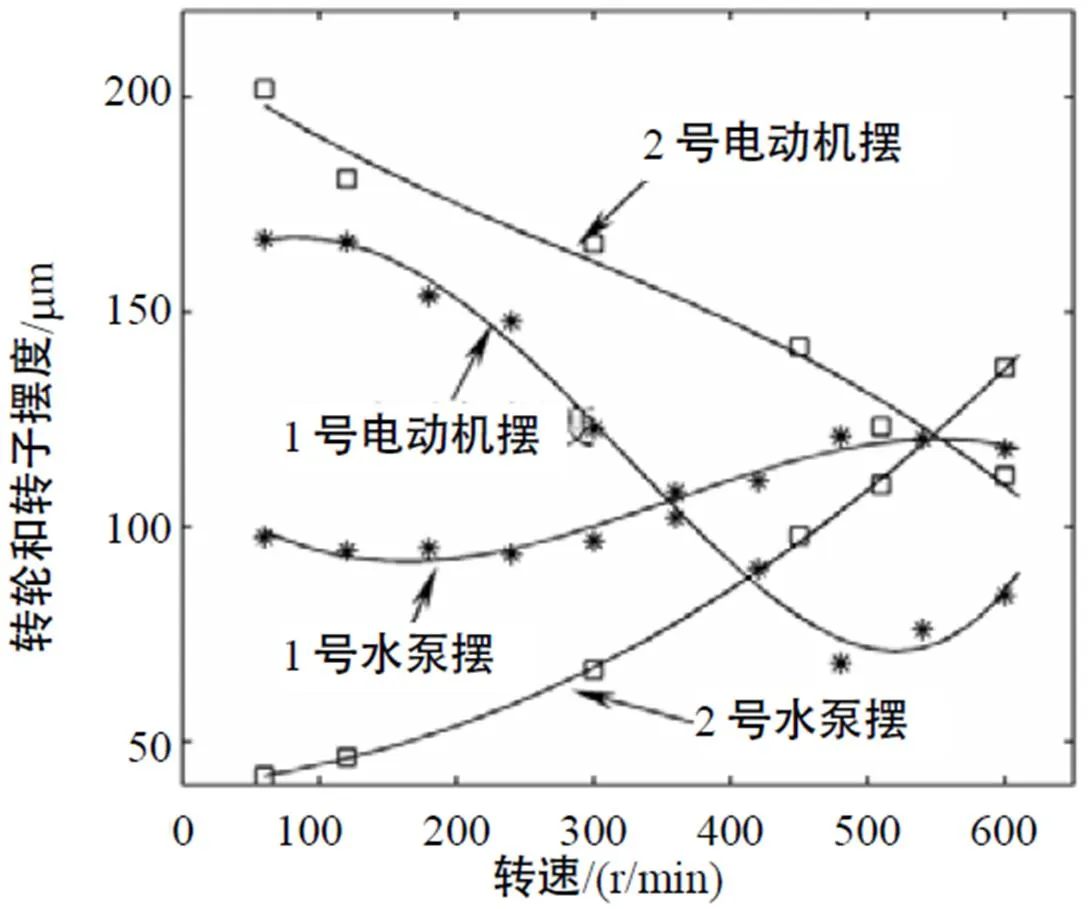
图2 转子和转轮摆度随转速变化拟合曲线
根据前面所述内部因素和外部因素的基本特征,对照图2可以看出:
(1)从图2看,从电动机摆度随转速增加而减小,显然不是电动机质量偏心引起的振动。无水启动中,电动机不同转速下不平衡磁拉力不同,由于1号机组和2号机组变化趋势基本一致,因此,也应该不是电动机电磁不平衡外力引起的。水泵转轮摆度随转速增加而增加,两条水泵趋势基本一致。无水启动条件下,转轮上的附加作用力近似为0。基于上述几方面的分析,可基本确定,2号水泵摆度大的原因不是由于外部因素引起的。
(2)按本文的分类,内部因素主要设计固有频率转速和支承刚度。从图2中看出,2号机组电动机摆度和水泵摆度随转速增大明显减小,表明与转速相关,从式(16)中几个传递矩阵的构成来看,只有A矩阵与转速相关。从A的表达式来看,若ω较大,则角速度的影响不明显,反之,ω较小,则角速度的影响会变得明显。因此,可确定2号水泵机组振动偏大的原因是电动机转子和水泵转轮固有频率偏低,即轴承支撑刚度偏低。而且,主要问题在于电动机转子上下导轴承或机架支承刚度小造成的。
上述分析属于定性分析,分析结论与基于工程经验的直观分析结论是一致的。这种定性识别可为水泵机组轴系振动指明解决振动的方向,是一种粗略的振源识别方法。
限于篇幅,本文对数值计算问题不再进行分析和讨论。有关数字计算和进一步的定性分析方法,尚有待进一步深入研究。
5 结论
本文提出的振动识别方法,尝试从理论上揭示可测轴系振动参数与轴系运动参数之间的内部关联耦合机制,并且以转移矩阵形式给出了这种内部关联机制,具有重要的理论意义。
实际运行中的水泵机组,由于轴系振源的多源性和多场耦合特性,可能存在多振源耦合作用的情况。而本文对振源识别的讨论上,仅考虑了单一振源的识别问题,这是本文的局限性。对多源耦合振动问题、以及振源特征的数字计算及其分析理论方面尚需开展进一步的深入研究。
[1] 赵顺萍, 肖泽, 孙凝, 等.应用振动监测与故障分析诊断技术提高泵站设备管理水平[J]. 中国给水排水, 2015, 31(6):105-108.
[2] 黄澄, 朱雪明, 肖泽. 设备在线振动监测与故障分析诊断技术在大型水泵机组中的应用[J]. 给水排水, 2010, 36(5):53-57.
[3] 郝春明, 韩骏, 刘红伟, 等. 常熟水利枢纽泵站水泵机组振动监测研究[J]. 水利与建筑工程学报, 2012, 10(3), 92-95,100.
[4] 李斌, 郑源, 徐瑛丽. 大中型泵站机组特性测试与诊断系统研究[J]. 中国农村水利水电, 2012, 8, 158-161,164.
[5] 付强, 袁寿其, 朱荣生, 等. 1000MW级核电站离心式上充泵转子轴系的扭振特性[J]. 排灌机械工程学报, 2013, 31(5):394-400.
[6] 于建, 伦功仁, 赵峰, 等. 水泵机组动态特性与流场分析[J].水泵技术, 2015,4:33-37.
[7] 李忠, 杨敏官, 张宁. 变工况下轴流泵装置振动特性实验研究[J]. 工程热物理学报, 2013, 34(5):866-869.
[8] 李伟, 季磊磊, 施卫东, 等. 混流泵启动过程转子轴心轨迹的试验研究[J]. 机械工程学报, 2016, 89-99.
[9] 丁凯, 付士鹏, 朱霄珣, 等. EMD在水泵非线性振动分析中的应用[J]. 给水排水, 2013, 39(8), 120-122.
[10] 史丽萍, 汤家升, 张晓蕾, 等. RBF和改进BP神经网络在水泵振动故障诊断中的应用比较[J]. 大电机技术, 2014(4):59-62,80.
[11] 刘文进, 曹宏涛, 张鹏, 等. 设备冷却水泵转子系统振动特性研究[J]. 水泵技术, 2016, 6,29-33.
[12] 仇宝云. 大型立式泵机组轴线摆度的分析与处理[J]. 大电机技术, 1994(6): 7-11.
[13] Zeng yun, Zhang lixiang,guo yakun,Qian jing,Zhang chengli. The generalized Hamiltonian model for the shafting transient analysis of the hydro turbine generating sets[J]. Nonlinear Dynamics, 2014, 76(4), 1921-1933.
Vibration Source Identification of Water Pump Units Based on Shafting Trajectory
LI Yaohui1, ZHU Shuangliang2
(1. Yunnan Water & Hydraoopower Investment Co., Ltd., Kunming 650051, China; 2. Yunnan Water Conservancy and Hydropower Investment Niulan River to Dianchi Lake Water Diversion Project Co., Ltd., Kunming 650051, China)
The vibration inducement of large water pump unit has polyphyly, and its analysis depends mainly on engineering experience, which has a certain uncertainty. Based on the motion equation of centroid trajectory of electromotor rotor and pump runner in vertical pumping units, the relationship between the measurable vibration throw and motion parameters of shafting is revealed by the theoretical derivation. Vibration source of water pump units is divided into the inner factor and external factor. Transfer matrix from the inner factor to shafting throw and from the external factor to shafting throw are established respectively. According to characteristics of vibration source, the vibration source identification based on the observation of shafting throw is proposed. Lastly, a example of pump station is analyzed. Proposed method in this paper reveals the coupling dynamics mechanism between measurable throw parameter and motion parameter of shafting system, and has the reference value for theoretical and engineering.
water pump units; motor; shafting vibration; trajectory equation; vibration source identification; transfer matrix
TM32
A
1000-3983(2017)04-0057-05
2017-01-20
李耀辉(1960-),1983年8月毕业于云南工学院电力系水电站动力设备专业,从事水力机械稳定、故障分析研究。高级工程师、副总工程师。
朱双良(1971-),1994年7月毕业于云南工学院电力系水利水电动力工程专业,从事水力机械稳定、故障分析研究。工程师、总工程师(通讯作者)。
