冲击式水轮机发展概况与新技术

张征骥



冲击式水轮机发展概况与新技术

张征骥

（水力发电设备国家重点实验室（哈尔滨大电机研究所），哈尔滨 150040）

本文首先介绍了冲击式水轮机一百余年来以试验为基础的发展状况。然后重点介绍了近十余年来在理论创新方面的一些重要成果。其具体内容都以两本专著(德，英文)为基础，主要包括水轮机水动力特性分析计算以及设计方法等。其一，指出了摩擦损失是冲击式水轮机中最大损失并给出了计算方法。其二，飞逸速度的计算非常简单可靠。其三，给出了冲击式水轮机的主方程与完整特性曲线。此外，还给出了用于计算水斗根部最大机械应力的相似定理等。本文旨在以导读的方式为冲击式水轮机领域的工作者提供尽可能全面的技术帮助。

冲击式水轮机；粘性摩擦损失；飞逸速度；主方程；相似定理；喷嘴调节模式；分水刃磨损

0 冲击式水轮机百年史

冲击式水轮机是由Pelton在十九世纪末发明并首先申请专利的。一百多年来，冲击式水轮机在水力发电领域得到广泛应用。与其同时，该型式水轮机在设计与制造等技术方面也取得了巨大进步与发展。在设计方面，包括喷嘴与转子的设计，冲击式水轮机的效率通常可以达到91%。在制造方面，水轮机转子已由最初的生铁生钢铸造发展到今天的以基盘不锈钢锻造以及水斗数控切削为主的先进生产方式。由于材料与生产工艺的发展，大型冲击式水轮机的单机输出功率已达到423MW之多(瑞士Bieudron)[1, 2]。

在水力设计方面，冲击式水轮机高效率的实现主要依赖于（1）实验室内对各不同设计改进的反复验证;（2）设备运行方面的经验积累。这方面的研究工作更多地表现在对射流的测试研究。其基本方法就是用最简单的毕托管测量射流中的速度分布[3, 4]。此外就是对高速射流进行摄像，以观测射流的表面结构以及射流的扩展与稳定性[5]。很多情况下，这种测量与观测很容易导致对射流结构判断错误。比如，常见报导的0.2度的射流扩展事实上只是射流表面与空气作用的结果。整体射流的扩展角不会超过0.02度。对射流的精确测量则是在新世纪初首次用激光多普勒方法实现的[6]。该方法不仅精确地测量了射流的轴向速度，同时还精确地测量了射流横断截面内的二次环流。后者在对射流与转子的相互作用方面同样起着关键作用。关于射流与转动水斗的相互作用以及水斗内和水斗出口的流动情况，人们通常都借助于频闪观测器做直接观察，并由此来确定转子切向速度与射流速度的最佳比。还有在转子上直接固定摄像机用以观察水斗内的相对流动[7]。此外，在水斗表面安装压力传感器用以测量压力大小与分布[2, 8-10]，其主要目的却仅仅是用来验证计算流体力学的模拟运算。其它方面，如文献[11]所载，人们还在原型机上测量了水斗分水刃磨损与效率损失的关联程度。

与试验相比，理论方面的研究还存在相当大的空白。一百余年来，除了伯努利方程用于计算喷嘴射流的速度之外，再没有一个流体力学原理的应用，能够圆满地用于描述射流与转子的相互作用以及水斗内水的流动与相关力学效应。这方面的理论缺失甚至明显表现在对离心力和科氏力在能量交换过程中的各自作用都缺乏理论分析与计算。对于高达90%~91%的水动力应用效率，即对于实际存在的9%~10%的效率损失，人们只能对大约4%的效率损失做出基本定位。对于未知的5%~6%的效率损失来源缺乏更深入的研究。大家都知道，进一步提高冲击式水轮机的效率，即使是0.5%，都已成为该领域的长期努力方向。很多部门还注入了大量资金。可是，由于对效率损失来源缺乏全面了解，人们也就始终没有认识到减小损失的最大潜力所在。

另一方面，高速射流在进入转动着的水斗之后，虽然其相对流速只有射流速度的一半左右，水流的相对运动所引起的摩擦损失必然是构成整个效率损失的一个重要组成部分。可是，对于相对系统中的摩擦阻力是以怎样的物理方式最终引起绝对系统中的效率损失这一命题，还没有估算方法。这也成为在冲击式水轮机研究方面长期以来缺少理论分析与计算的印证之一。

其它如水轮机飞逸过程与飞逸速度的确定等，无不都由试验来完成。

进入新世纪之后，随着计算机运算速度与网格细密化程度的大幅提高，计算流体力学(CFD)的应用在冲击式水轮机领域也呈现较快增长趋势。这其中既包括对射流的模拟，还主要包括了对水斗内以及水斗出口流动分布的模拟[12-13]。虽然计算流体力学在一定程度上丰富了复杂流动的研究方法，但是，计算流体力学的功能依然局限于仅仅“描绘”各流动过程与各不稳定阶段流动情况。由于CFD方法总是对给定的特定流动进行数值模拟计算，无法揭示各流动普遍规律与机理。

为此，瑞士水电公司KWO批准了从理论上全面开发该式水轮机技术的建议并启动了相关项目。大部分成果展现在专著[14]、[15]中。

1 新理论概述

1.1 水斗内粘性摩擦损失为各损失中最大

首先，水斗内粘性摩擦损失是总损失中的一部分。由于粘性摩擦发生在相对(即旋转)系统中，它对绝对系统中的效率的影响是一个复杂的物理过程。一方面，摩擦本身是一种力，直接推动或阻碍水斗的转动。另一方面，粘性摩擦引起水流相对速度减缓，进而导致流水层底部压力下降，水斗推动力折损，最终间接导致水轮机效率损失。这一直接与间接影响的叠加是水斗内粘性摩擦的总效应，即相对运动系中的粘性摩擦导致绝对系中的效率损失。从这一原理出发，文献[14]、[15]中均推导出了相应过程联系，被命名为水机水流摩擦定理(Flow Friction Theorem即FFT)。

水斗内粘性摩擦损失的近似计算由下式给定：

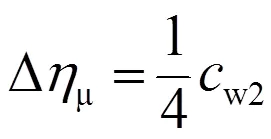
（2）

图1 射流及水斗内水流分布

这就是摩擦数的物理意义。从水斗进口到出口相对速度的变化为。按照前面的假设计算，摩擦数即意味着。相对速度的变化在10%左右，这一百分比变化与人们通常假设的实际情况相符合。

由于粘性摩擦损失是冲击式水轮机中的第一大损失，为了提高水轮机的效率，水斗的机械表面应尽量保持光滑。

1.2 飞逸速度及其计算方法

在冲击式水轮机的设计阶段，飞逸速度是一个极其重要的设计参数。过高的飞逸速度会导致发电机的设计困难。一直以来，实验室模型试验是确定冲击式水轮机飞逸速度的唯一途径。实验室方法也因此而代价高，费时长。而一些设计手册中给出的参考数据一般为额定转速的1.8~1.9倍。由于该数据过分粗糙，所以常常无法满足需要。从原理上看，由于飞逸速度发生在射流与转动水斗不发生相互作用的情况下，所以归根到底它是一个与射流速度有关的参数。通过几何推导，飞逸速度下转子的切向速度与射流速度的比值由下式给出：

（5）

由公式（4）计算出的飞逸速度，经与多项试验值比较，其误差均小于1%。此结果证实了公式（4）的准确性与实用性。

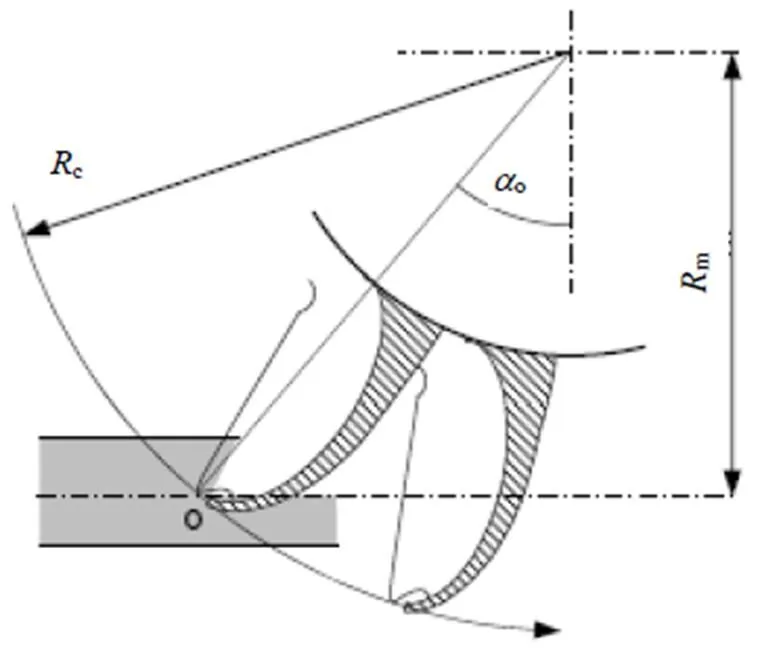
图2 水斗切口在切截射流轴线时的位置与位置特征角

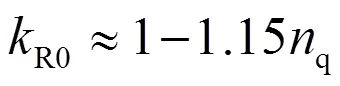
顺便需要指出的是，对于冲击式水轮机，几乎所有设计参数都可以用比转速准确且又唯一地表达。对此，文献[14]、[15]中都给出了详细列表。

1.3 水轮机完整特性曲线与主方程

在推导冲击式水轮机的特性曲线（即效率曲线）时，人们常常从动量原理出发，假设射流与水斗在直线上做相对运动。由此得出两点：第一，当水斗的运动速度是射流速度的一半时（k=0.5），能量交换效率达最大值。第二，特性曲线的下半段与上半段呈对称分布。尤其是在水斗的运动速度等于射流速度时，水轮机效率为零。实际中的水轮机特性曲线一概偏离这两点虚拟。这是由水轮机的实际转动而非平动所决定的。

大家知道，冲击式水轮机的最大效率常常发生在当水斗的切向速度等于射流速度的约0.47倍时。此外，特性曲线的上半段拥有区别于下半段的特殊地方。由于转子的转动，在转动速度超过一定的值时，部分射流将透过水斗逃逸过去，从而不作任何能量交换。逃逸射流与总射流的比是转子转速的函数，称为射流作用度，用Q表示。文献[14]、[15]中均给出准确计算公式。对应于全部射流逃逸水斗的转速称之为转子的飞逸速度。由上节可知，冲击式水轮机的飞逸速度并非额定速度的两倍。这是区别于平动水斗情况的一大方面。

考虑到冲击式水轮机的最大效率发生在速度比k,N, 通常有k,N=0.47左右，再考虑到水斗内粘性摩擦的影响以及射流逃逸与转速的关系，冲击式水轮机完整特性曲线可由下式给出：

该方程亦可称为冲击式水轮机的主方程。其中，2是水斗出口倾角，通常取170°左右。是摩擦数，见式（2）。

图3给出了由计算得到的某一冲击式水轮机的完整特性曲线。可以看出，曲线的上半部发生重大变异。对应于效率等于零的转速就是飞逸速度。

如果假设2=180°和k=k，则有射流作用度R=1。从式（7）可得h=1-c2/4。其中c2/4恰好是水斗内粘性摩擦引起的效率损失，见式（1）。

事实上，上述式（7）既包含水斗出口损失，还同时包括了粘性摩擦损失和射流逃逸损失。在额定工况下，射流逃逸损失为零。水斗出口损失相对于粘性摩擦损失通常又可忽略不计。

在公式（7）以及图3中所示实际特性曲线的基础上，水轮机转子从额定转速到飞逸速度的加速过程也就容易计算出来。其计算过程在参考文献[14]、[15]中都有描述。

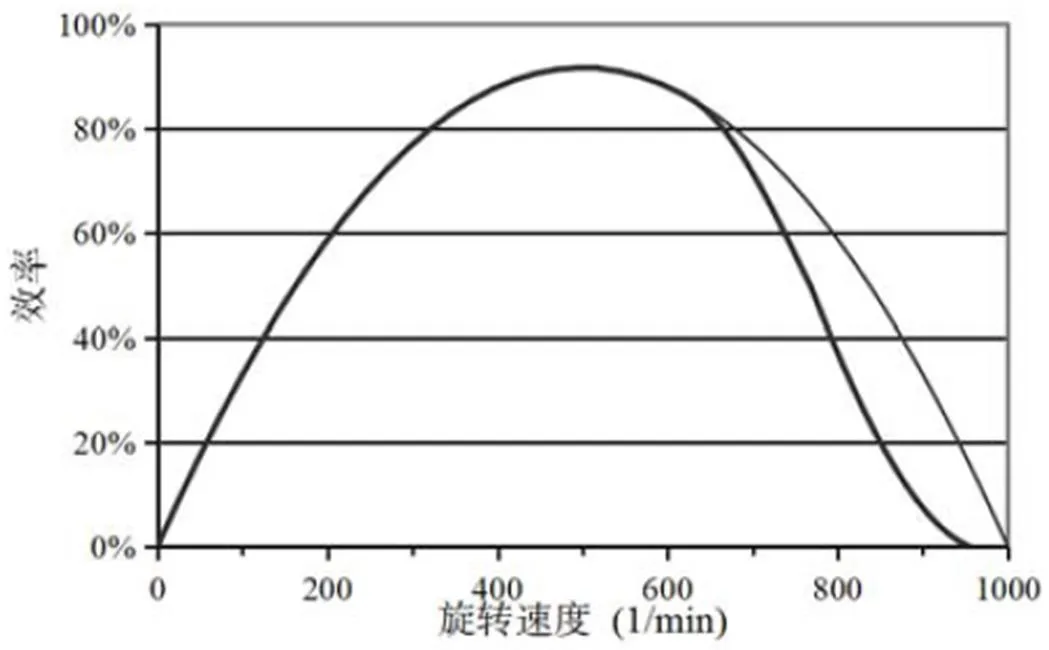
图3 冲击式水轮机实际特性曲线

1.4 水斗机械强度与相似定理

冲击式水轮机的水斗受高速射流冲击，水斗根部承受周期性应力变化。为了确保最大机械应力处于允许范围内，除了使用高性能材料之外，再就是优化设计，以求降低最大应力值。对最大应力的可靠计算通常使用有限元法（FEM）。但是，常常有这样的情况，就是人们仅仅需要对可能的应力状况做出初步评估，而不是每次都做复杂的有限元数值计算。事实上，冲击式水轮机水斗造型都相似。假设一已知水斗在某给定受力情况下根部应力为已知（如图4所示），比如通过有限元法计算而得，那么，任何水斗在任何其它受力情况下的根部应力都可以通过相似定理而即刻获得。与此相对应，存在三个相似定理，分别述及如下。其中下标1代表已知应力值的水斗，下标2代表待解应力值的水斗。此外，下标1和下标2也指处于两种不同工作状态下的同一个水斗。

图4 水斗结构机械应力分布及观测区。

第一相似定理：

待解水斗有着与已知水斗大小不同的尺寸()。同时射流冲击力()也分别不同。两水斗根部最大应力比为

作为基本定理，该第一相似定理还适用于同一或相同水轮机转子()不同负荷下(，)水斗根部最大应力比的计算。由此推导出第二和第三相似定理。

第二相似定理：

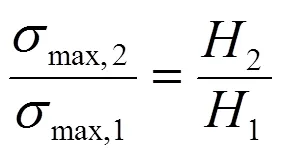
第三相似定理：

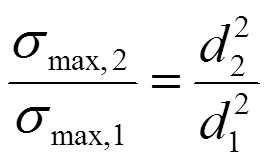
1.5 喷嘴调节模式与水锤效应

冲击式水轮机输出功率的调节是通过喷嘴调节实现的。这个调节过程又统称为过渡过程。这其中还包括喷嘴的开启与关闭。由于每次负荷的调节以及喷嘴开启或关闭都会引起整个水力系统内的水锤效应，即引起压力波和压力升高，所以，喷嘴的开启与关闭模式是决定过渡过程中水锤效应的关键。以喷嘴关闭为例，为了实现最平稳过渡，在给定的时间内()，喷嘴喷针从额定位置()到完全关闭宜选用下述二次函数模式：

图5给出了额定工况与半工况下喷嘴的关闭模式。其中曲线2是曲线1的向左平移。如果是以调节为目的，所给曲线依然可以使用。实践中，二次函数型的调节曲线可以直接编入调节程序中。

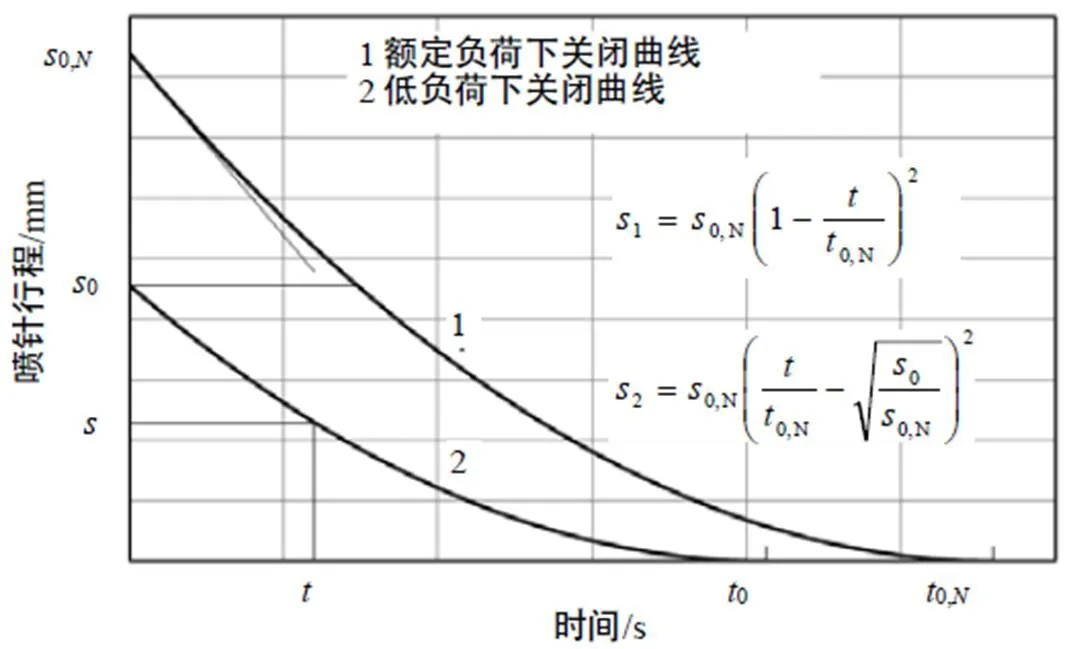
图5 二次函数型的喷嘴调节曲线

1.6 分水刃磨损及其对效率的影响

工程实际中，很多冲击式水轮机受水中含砂量的影响发生机械磨损。其中水斗表面的磨损会因表面粗糙度增加按照FFT定理（见1.1节）影响机器效率。与此不同，分水刃的磨损则从另一物理原理影响机器效率。根据图6，因机械磨损而呈现一定宽度的分水刃导致部分射流脱流。其脱流程度取决于射流中各垂直射流层有限宽度与分水刃磨损宽度的比值()。由于射流脱流的存在，脱流部分可视为直接损失。基于这一物理模型，由分水刃磨损而导致的效率损失可以估算出来。图7示出了不同负荷下计算结果比较。可以看出，在额定射流情况下，当分水刃磨损宽度达到水斗宽度的4%时，由此引起的效率损失为4%。在半工况下，效率损失还要增加。

图6 分水刃磨损与射流脱流模型

图7 分水刃磨损与相应效率损失

图7中的计算结果在文献[15]中得到了实际测试结果[11]的验证，还对砂粒在水斗中的运动轨迹做了较为详细的推导与计算。这对进一步研究水斗内砂磨损失具有指导意义。

2 一个有趣的虚拟思考题

冲击式水轮机的每一个水斗都是由两个对称的半水斗组成。所以，各半水斗与射流交换的能量相同。现假设一个水斗由两个不对称的半水斗(A,B)组成，如图8所示。且问，当水斗的切向速度等于射流速度的一半时，两个不对称的半水斗与射流的能量交换是否相同？其它附加条件为理想流体并且重力加速度的影响忽略不计。这一虚拟思考题有助于理解旋转系统中伯努利方程的应用。

图8 虚拟非对称半水斗中能量交换之同与不同(U=0.5C)

3 结束语

冲击式水轮机的水动力特性是由从射流喷嘴到水斗出口各不同环节组成并决定的。除了本文中所阐述的几个方面外，其完整的水动力特性还包括射流测量与分析，射流中二次环流及水珠串形成机理与危害，喷嘴内各作用力平衡，水斗内沿径向粘性流动分析，水斗出口条件与设计，出口损失，转动系中速度能量方程及其在射流中的应用，风阻损失，多喷嘴情况下相邻两喷嘴间最小夹角，水轮机设计，水斗椭圆曲面计算，水斗数计算，模型机效率修正，飞逸过程等。所有这些内容都包含在文献[14]、[15]中。

[1] Keck, H., Vullioud, G., Joye, P.. Commissioning and operation experience with the world’s largest Pelton turbines Bieudron[C]. Hydro Vision, Charlotte, USA, 2000.

[2] Angehrn, R.. Safety engineering for the 423 MW-Pelton-runners at Bieudron. Proc[C]. 20thIAHR Symposium, Charlotte, N,C, USA, 2000 .

[3] Berntsen, G., Brekke, H., Haugen, J., Risberg, S. Analysis of the free surface non-stationary flow in a Pelton turbine[C]. Hydro 2001, Riva del Garda, Italy, 2001.

[4] Brekke, H.. State of the art of small hydro turbines versus large turbines[C]. Hydro 2005, Villach, Austria, 2005.

[5] Staubli, T., Hauser, H.. Flow visualization - a diagnosis tool for Pelton turbines[C]. Fifth IGHEM conference, Lucerne, Switzerland, 2004.

[6] Zhang, Zh., Casey, M.. Experimental studies of the jet of a Pelton turbine[J]. Proc. IMechE Vol. 221 Part A: J. Power and Energy, p1181-1192, 2007.

[7] Solemslie，B.，Dahlhaug，O.. A reference Pelton turbine - High speed visualization in the rotating frame[C]. IAHR, 28th Symposium on Hydraulic Machinery and Systems. Grenoble, France, 2016.

[8] Kvicinsky S., Kueny J., Avellan F., Parkinson E.. Experimental and numerical analysis of free surface flows in a rotating bucket[C]. Proc. 21stIAHR Symposium on Hydraulic Machinery and Systems, Lausanne, Switzerland, 2002.

[9] Perrig, A., Avellan, F., Kueny, J., Farhat, M., Parkinson, E.. Flow in a Pelton turbine bucket: Numerical and experimental investigations[J]. Journal of Fluids Engineering, Transactions of the ASME 128, p350-358, 2006

[10] Zoppé, B., Pellone, C., Maitre, T., Leroy, P.. Flow analysis inside a Pelton turbine bucket[J]. Journal of Turbomachinery, Transactions of the ASME, Vol. 128, p500-511, 2006.

[11] Maldet, R.. Pelton runner with high erosion caused by glacier sediment: assessment and measures[C]. 15thInt. Seminar on Hydropower Plants, Vienna, Austria, p639-646, 2008.

[12] Parkinson, E., Neury, C., Garcin, H., Weiss, T.. Unsteady analysis of a Pelton runner with flow and mechanical simulations[C]. Hydro 2005, Villach, Austria, 2005.

[13] Muggli, F., Zhang, Zh., Schärer, C., Geppert, L.. Numerical and experimental analysis of Pelton turbine flow, Part 2: The free surface jet flow[C]. Proc. 20thIAHR Symposium, Charlotte, NC, USA, 2000.

[14] Zhang, Zh..Freistrahlturbinen[M]. Springer-Verlag, 2008.

[15] Zhang, Zh.. PeltonTurbines[M]. Springer-Verlag, 2016.

Development and New Technology of Pelton Turbines

ZHANG Zhengji

(State Key Laboratory of Hydro-power Equipment(HILEM), Harbin 150040, China)

Thisarticle firstly reviews the historical developments of the Pelton turbine, based on experimental investigations. Thenit introduces, for more details,somenew and significant achievements in the past decadebased on theoretical analyses. All these achievements are referred to two monographs in both German and English. They includethe hydro-mechanical analyses and computations as well as the design methods for Pelton turbines.Firstly, the viscous friction loss has been confirmed to be the biggestloss in the system efficiency, to which the computational method is given. Secondly, the runaway speed of the Pelton turbine can be very simply and accurately computed. Thirdly, the master equation of the Pelton turbine together with the complete characteristics has been presented. In addition, three similarity theorems have been revealedfor easily estimating the mechanical stress in the root area of the Pelton buckets. This article, thus, aims to provide a reading guidanceto all engineers and researchers in the field of Pelton turbines in form ofthe most comprehensive technical assistance.

Pelton turbines; viscous friction loss; runaway speed; master equation; similarity laws; closing lay of the injector nozzle; eroded main splitters

TK730

A

1000-3983(2017)04-0001-06