营口站最低潮位频率计算

2017-08-17倪皖南陈理想谷宏亮王晶晶

东北水利水电 2017年8期

关键词：皮尔逊负值潮位

倪皖南，陈理想，谷宏亮，王晶晶

（1.辽宁省沈阳水文局，辽宁沈阳110043；2.水利部松辽水利委员会，吉林长春130021；3.中国电力建设集团有限公司，北京100048；4.辽宁省水利水电勘测设计研究院，辽宁沈阳110006）

营口站最低潮位频率计算

倪皖南1，陈理想2，谷宏亮3，王晶晶4

文中通过分析皮尔逊-Ⅲ型分布时最低潮位（负值系列）与最高潮位（正值系列）统计参数对应的关系，寻找出最低潮位的计算方法，计算营口站设计最低潮位，同时采用极值Ⅰ型分布估计设计最低潮位，合理选取最低潮位设计值。

设计潮位；频率计算；营口站

我国设计潮位频率分析的线型一般采用皮尔逊-Ⅲ型分布和极值Ⅰ型分布。对参数估计方法，极值Ⅰ型分布参数固定，不能根据实测经验点据进行调整；皮尔逊-Ⅲ型分布实际应用中以矩法初步估计参数，经验适线法确定参数为主[1]。因最低潮位系列为负数系列，与设计最高潮位不同，最低潮位值越低越稀遇，因此完全按照设计最高潮位时从高到低排序进行频率分析的方法已不适用，而国内最低潮位频率分析参考资料较少，文中通过分析皮尔逊-Ⅲ型分布时，最低潮位（负值系列）与最高潮位（正值系列）统计参数对应的关系，寻找出最低潮位的计算方法，以营口站为例，计算营口站设计最低潮位，同时采用极值Ⅰ型分布估计设计低潮位，合理选取最低潮位设计值。

1 皮尔逊-Ⅲ型分布

根据《海港水文规范》[2]，设计潮位频率分析的线型，在受径流影响的潮汐河口地区，宜采用皮尔逊-Ⅲ型分布曲线，在海岸地区可采用极值I型或皮尔逊-Ⅲ型分布曲线。

皮尔逊-Ⅲ型分布概率密度函数如下：

式中：Γ（α）——α的伽玛函数；α，β，a0——3个参数。皮尔逊-Ⅲ型分布概率密度曲线见图1，是一条一端有限，一端无限的不对称单峰曲线。左端x为负值系列的概率密度曲线，右端为其绝对值系列（以x′表示）的概率密度函数。

样本的统计参数有均值xˉ，变差系数Cv和偏态系数Cs。有一正值系列xi，即概率密度函数为图1中右侧曲线所示时，则样本统计参数如下：

图1 皮尔逊-Ⅲ型分布概率密度曲线

皮尔逊-Ⅲ型分布概率密度函数的3个参数与样本的3个参数关系如下：

皮尔逊-Ⅲ型分布的3个参数：α′=α，β′=-β，a0′=-a0

作极小值的频率分析时，其数值须由小到大排序，而作极大值频率分析时，其数值须由大到小排序，负值系列的概率见下式：

同一概率P所对应的随机变量xp′=-xp，即正值系列时大于等于某一设计值xp的频率为P，值越大越稀遇；负值系列时小于等于某一设计值-xp的频率为P，值越小越稀遇。

2 极值Ⅰ型分布

对于极值Ⅰ型分布，参数估计具体公式如下：

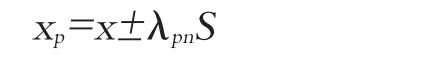
式中：xp——设计年频率P的高（低）潮位，高潮位用正号，低潮位用负号；λpn——与设计年频率P、资料年数n有关的函数；xˉ——n年中的最高（低）潮位值xi的平均值；S——n年的xi的均方差。

3 实例研究

营口入海河口地区为辽宁省滨海低洼地区，该地区涝区特点是地势较低且排水常受潮水位顶托而导致排水时间受限，常常需靠抽排完成排涝任务。最低潮位的合理选取，对排涝工程设计来说非常重要，直接影响排涝工程的排涝效果和经济效益。

以营口潮位站1955年至2013年的最低潮位（负值系列）为样本，分别用皮尔逊-Ⅲ型分布和极值Ⅰ型分布估计参数。

3.1 皮尔逊-Ⅲ型分布

对营口站最低潮位（负值系列），根据最低潮位绝对值后的系列资料通过用最高潮位频率计算的方法求解出此系列资料的统计参数及设计值，最高潮位频率计算采用矩法初步估算统计均值、变差系数Cv和偏态系数Cs参数，采用经验适线法确定参数，Cs=3.5Cv。最高潮位设计值的负值即为最低潮位的设计值。最低潮位系列由小到大排序。用皮尔逊-Ⅲ型分布律方法推求营口站不同频率设计低潮位见表1。

3.2 极值Ⅰ型分布

经计算，营口站1955—2013年长系列低潮位统计特征值为：均值=-2.26m，S=0.189。用极值Ⅰ型分布律方法推求营口站不同频率设计低潮位见表1。

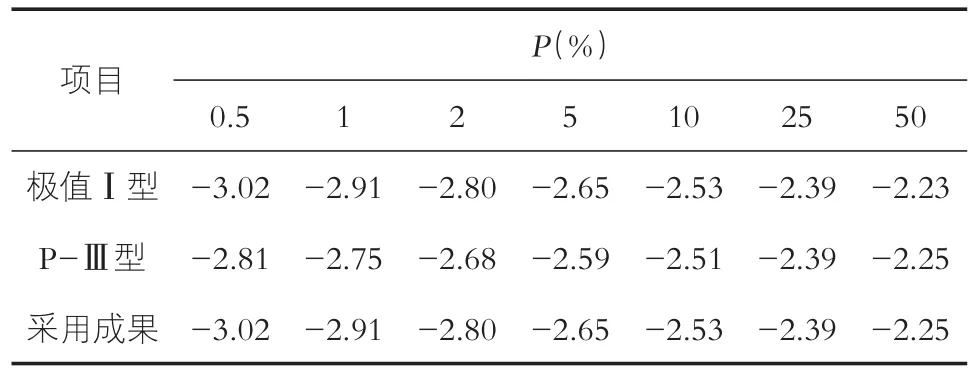
表1 营口站设计最低潮水位成果表m

营口站皮尔逊-Ⅲ型和极值I型两种方法计算的设计最低潮位成果接近，相差不大，极值Ⅰ型分布律方法计算的设计低潮位在两端上翘，P-Ⅲ型曲线相对来说较平顺。这与内外海潮位的变化规律相符合，一般来说，内海地区（即潮汐河口地区）受径流影响，潮位变化幅度小，宜采用皮尔逊-Ⅲ型分布曲线；外海潮位变化幅度大，宜采用极值I型分布曲线，也可采用皮尔逊-Ⅲ型分布曲线。

为安全计，采用两种分布计算的较低潮位值作为设计值。