纯电动汽车电子稳定控制及仿真*

方春杰

（重庆交通大学）

随着汽车高速化、车流密集化日趋明显，纯电动汽车的行驶稳定性和安全性备受人们关注。纯电动汽车在行驶过程中遇到高速大转向、侧向风干扰及高速移线等极限工况时，其轮胎侧偏角增大会致使轮胎侧偏力增大至侧向附着极限，使轮胎工作于非线性区域，此时汽车横摆角速度响应呈非线性变化[1]22-25，导致汽车偏离预定的行驶轨迹甚至出现失控状态，危及驾乘人员的人身安全。汽车电子稳定控制（ESC）主要用于控制汽车的横摆力矩，限制轮胎侧偏角在一定范围内，并在大侧向加速度和大侧偏角的极限工况下对汽车的行驶状态进行主动干预，以防止汽车在极限工况下失控[2]。文章以极限工况下的纯电动汽车为研究对象，引入ESC系统对其施加控制，在CarSim中建立整车动力学模型，并采用MATLAB/Simulink搭建汽车驱动电机模型和ESC系统的PID控制模型，在蛇形试验工况和高速大转向工况下对ESC控制策略进行联合仿真验证，以验证控制的有效性。

1 汽车动力学建模

1.1 整车动力学模型

为了反映汽车在极限工况下的运动状态以及动力学特性，在CarSim中建立参数化整车动力学模型，选取CarSim中前置前驱的D级轿车，其模型主要参数，如表1所示。

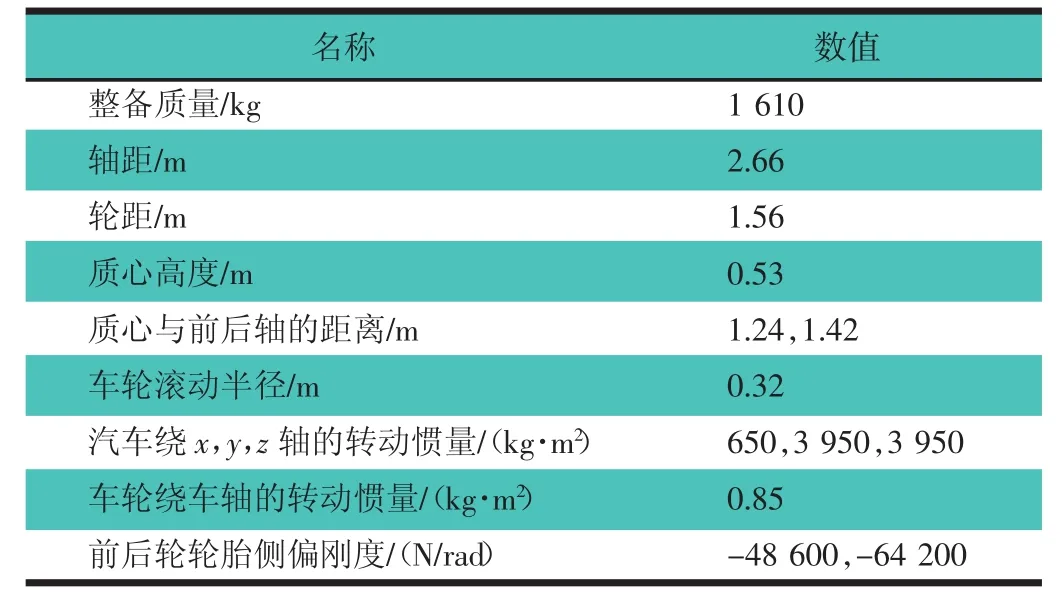
表1 整车动力学模型主要参数

1.2 驱动电机模型

由于CarSim中选用的D级轿车默认的动力源为传统的内燃机，而文章的研究对象为纯电动汽车，因而需要利用外部的电机模型替换已有的内燃机模型。采用试验建模法在Simulink中搭建纯电动汽车驱动电机模型，如图1所示。

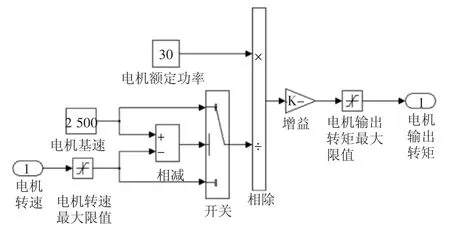
图1 纯电动汽车驱动电机模型图

该驱动电机的外特性曲线，即电机转矩与转速关系曲线，如图2所示。

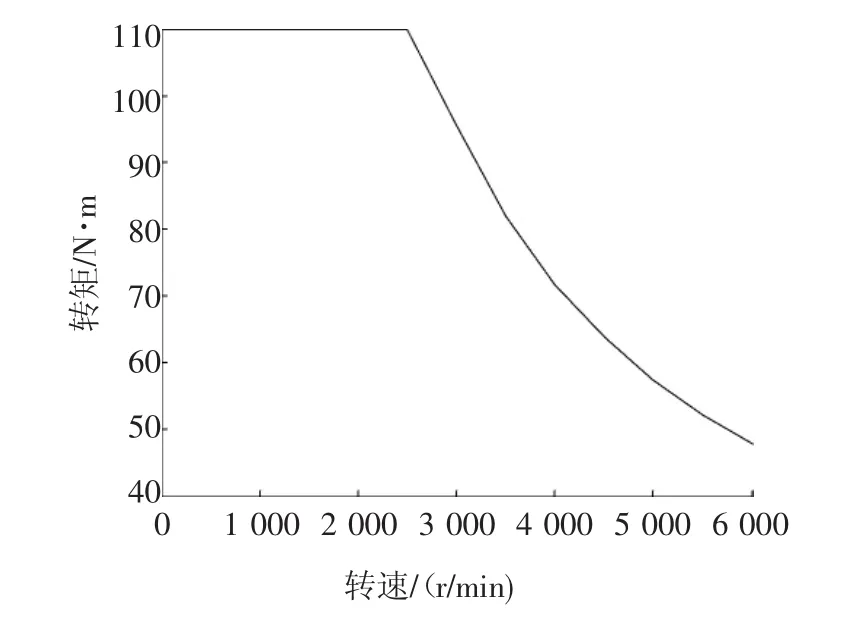
图2 驱动电机外特性曲线

1.3 汽车参考模型

为了计算汽车期望横摆角速度，考虑汽车的侧向运动和横摆运动，建立线性2自由度汽车参考模型[3]，其动力学方程，如式（1）所示。

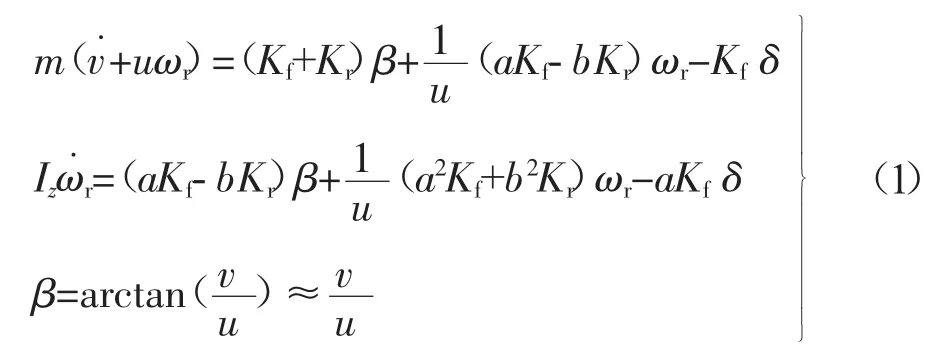
式中：m——整车质量，kg；

u——纵向车速，m/s；

v——侧向车速，m/s；

v˙——侧向加速度，m/s2；

a，b——汽车质心与前后轴之间的距离，m；

Iz——汽车绕z轴的转动惯量，kg·m2；

Kf，Kr——前后轮轮胎侧偏刚度，N/rad；

ωr——汽车横摆角速度，rad/s；

ω˙r——汽车横摆角加速度，rad/s2；

β——汽车质心侧偏角，rad；

δ——前轮转角，rad。

汽车等速行驶且在转向盘角阶跃输入下进入稳态响应时产生期望横摆角速度，此时汽车横摆角速度为定值，即在v˙=0，ω˙r=0 时，由式（1）可计算出汽车期望横摆角速度（ωr_desired/（rad/s））[4]，如式（2）所示。

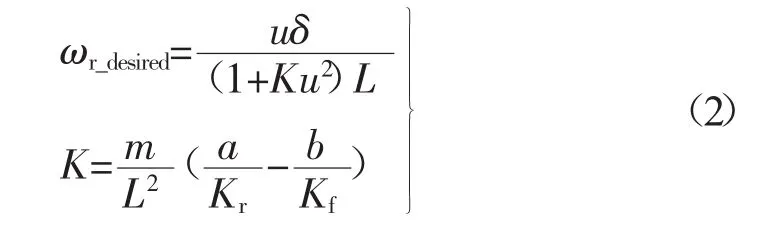
式中：L——轴距，m；

K——稳定性因数，s2/m2。

路面附着条件是影响汽车行驶稳定性和安全性的重要因素，必须加以考虑。随着轮胎侧偏角增大，轮胎侧偏力也迅速增大，从而导致轮胎达到路面附着极限，此时汽车参考模型计算出的期望横摆角速度值应由边界值代替。汽车期望横摆角速度边界值（ωr_desired_bound/（rad/s））的计算[5]，如式（3）所示。

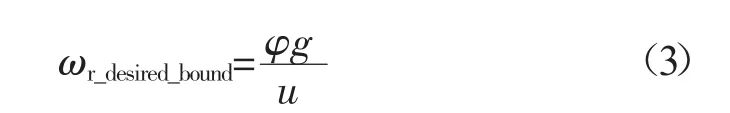
式中：φ——路面附着系数；

g——重力加速度，取9.8 m/s2。

2 汽车ESC系统控制

2.1 附加横摆力矩PID控制器设计

PID控制是一种常用、可靠且应用范围广泛的控制方法，主要由比例、积分及微分3个环节组成。其中，比例环节主要以一定比例控制并减小系统偏差，积分环节主要通过减小系统静误差以提高控制的稳定性，微分环节则主要对系统偏差的变化率进行控制以提高系统控制的响应速度[6]23-24。PID控制的一般表达式，如式（4）所示。

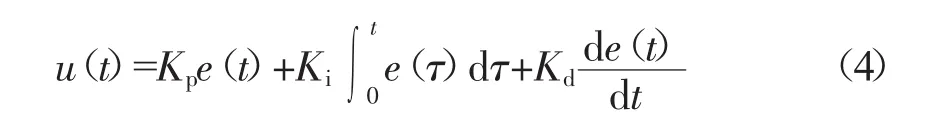
式中：e（t），u（t）——PID控制输入、输出变量；

Kp，Ki，Kd——比例、积分、微分环节系数。

基于PID控制方法，以汽车横摆角速度偏差作为输入变量，汽车附加横摆力矩作为输出变量[6]24-25，来设计汽车附加横摆力矩PID控制器，如式（5）所示。

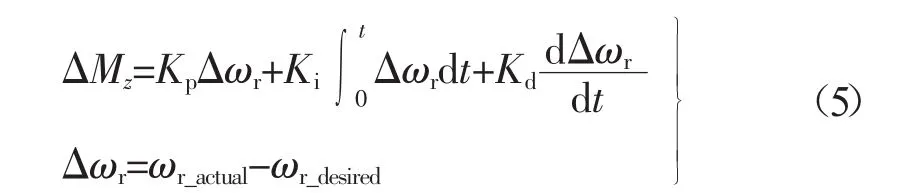
式中：ΔMz——汽车附加横摆力矩，N·m；

Δωr——汽车横摆角速度偏差，rad/s；

ωr_actual——汽车实际横摆角速度，rad/s。

2.2 汽车制动器制动力分配控制

汽车附加横摆力矩最终通过汽车制动器制动力分配实现。为了得到合理可控的附加横摆力矩，采用单侧车轮制动方式[1]27-29对汽车各车轮的制动器制动力进行分配。若制动车轮为汽车左侧2个车轮，则可得到汽车附加横摆力矩与其左前轮和左后轮制动器的制动力关系式[1]27-29，如式（6）所示。

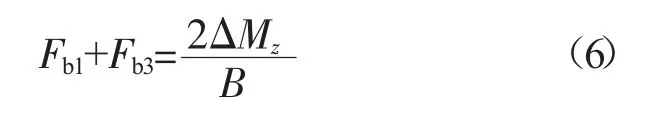
式中：Fb1，Fb3——汽车左前轮、左后轮制动器的制动力，N；

B——轮距，m。

汽车制动过程中，若车轮的滑移率保持不变，则车轮所受的地面制动力与其垂直载荷成正比。因而为了充分利用地面附着条件，根据单侧各车轮垂直载荷所占的比例实现车轮制动器制动力的动态分配[1]29-30，则左侧各车轮制动器的制动力，如式（7）所示

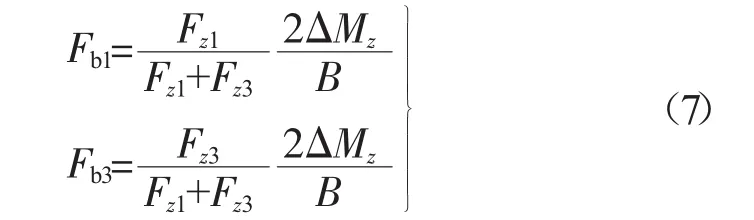
式中：Fz1，Fz3——汽车左前轮、左后轮垂直载荷，N。

同理，若单独制动汽车右侧车轮，则右前轮和右后轮所需提供的制动器的制动力Fb2，Fb4，如式（8）所示。

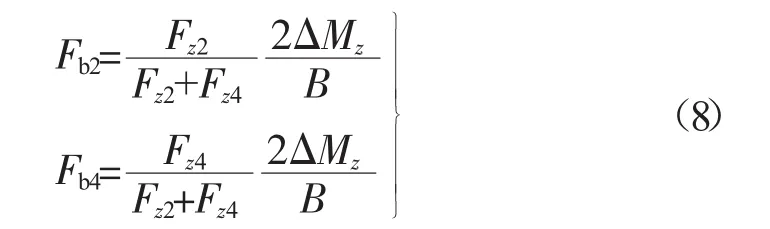
式中：Fb2，Fb4——汽车右前轮、右后轮制动器的制动力，N；

Fz2，Fz4——汽车右前轮、右后轮垂直载荷，N。

综上，可以得到纯电动汽车ESC系统的控制流程，如图3所示。

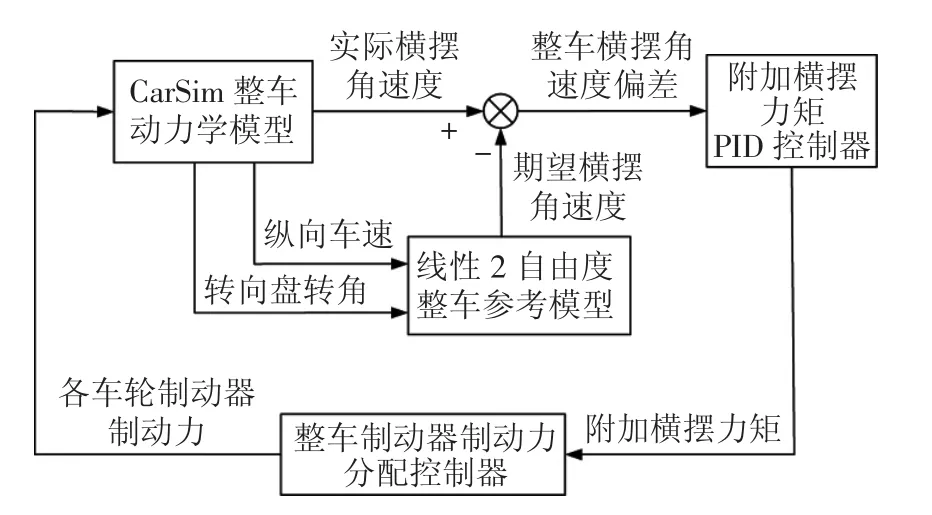
图3 纯电动汽车ESC系统控制流程图

3 汽车ESC系统仿真分析

3.1 蛇形试验工况仿真

汽车的初始速度为60 km/h，蛇形试验工况下汽车转向盘转角输入曲线，如图4所示，路面附着系数为0.8，仿真时间为10 s。在该工况下对有无ESC系统控制的纯电动汽车进行对比仿真。图5和图6分别示出蛇形试验工况下有无ESC系统控制的汽车横摆角速度和汽车质心侧偏角变化曲线。从图5和图6中可以看出，蛇形试验工况仿真前4 s，有、无ESC系统控制的汽车横摆角速度、质心侧偏角变化趋势及大小均基本保持一致；4 s之后直至该工况仿真结束，无ESC系统控制的汽车横摆角速度和质心侧偏角数值变化范围分别为 -0.48～0.49 rad/s和 -0.024～0.027 rad，而有 ESC系统控制的汽车横摆角速度和质心侧偏角数值变化范围则分别为 -0.511～0.032 rad/s和 -0.028～0.003 rad。因此与无ESC系统控制的汽车相比，有ESC系统的汽车横摆角速度和质心侧偏角变化幅度均显著减小，表明施加ESC系统控制后汽车的稳定性有所提高。

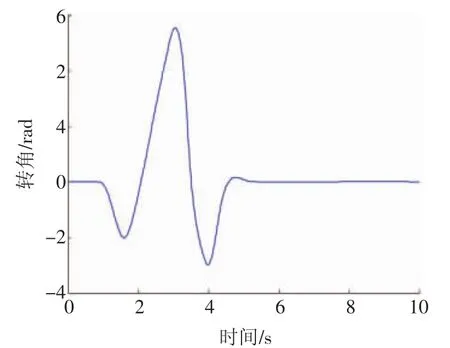
图4 蛇形试验工况下汽车转向盘转角输入曲线

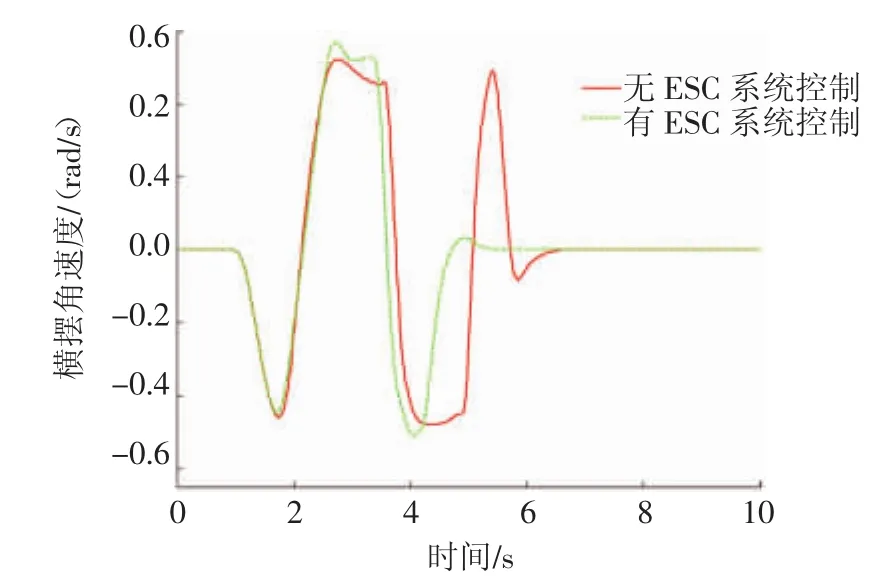
图5 蛇形试验工况下汽车横摆角速度变化曲线

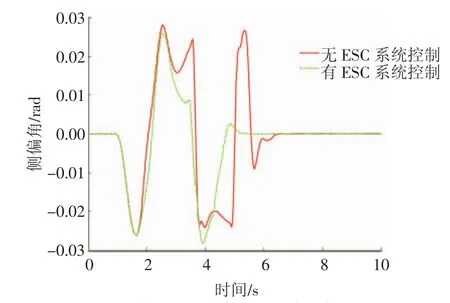
图6 蛇形试验工况下汽车质心侧偏角变化曲线

3.2 高速大转向工况仿真

汽车的初始速度为80 km/h，高速大转向工况下汽车转向盘转角阶跃输入，如图7所示，路面附着系数为0.8，仿真时间为20 s。在该工况下对施加ESC系统控制前后的纯电动汽车进行对比仿真。图8示出高速大转向工况下施加ESC系统控制前后的汽车横摆角速度变化曲线，从图8中可以看出，与施加ESC系统控制的汽车相比，未施加ESC系统控制的汽车横摆角速度变化更加剧烈，波动幅度较大，而施加了ESC系统控制的汽车横摆角速度波动较小，基本上趋于稳定值0.316 9 rad/s，因而施加ESC系统控制的汽车稳定性更好。图9示出高速大转向工况下施加ESC系统控制前后的汽车质心侧偏角变化曲线，由图9可知，施加ESC系统控制后的汽车质心侧偏角波动较小，其达到稳定状态所需的时间较短，而未施加ESC系统控制的汽车质心侧偏角波动较大，达到稳态所需的时间较长，因而可知施加ESC系统控制的汽车轨迹跟踪性更好。

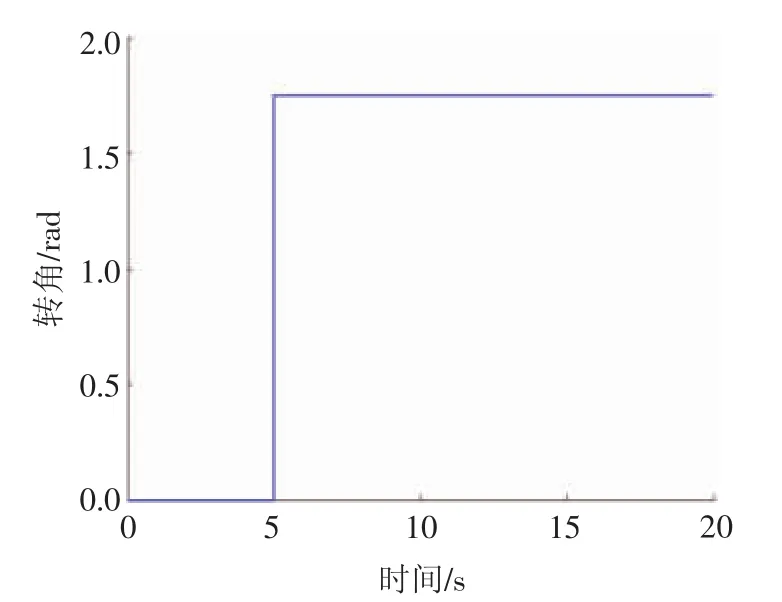
图7 高速大转向工况下汽车转向盘转角阶跃输入曲线

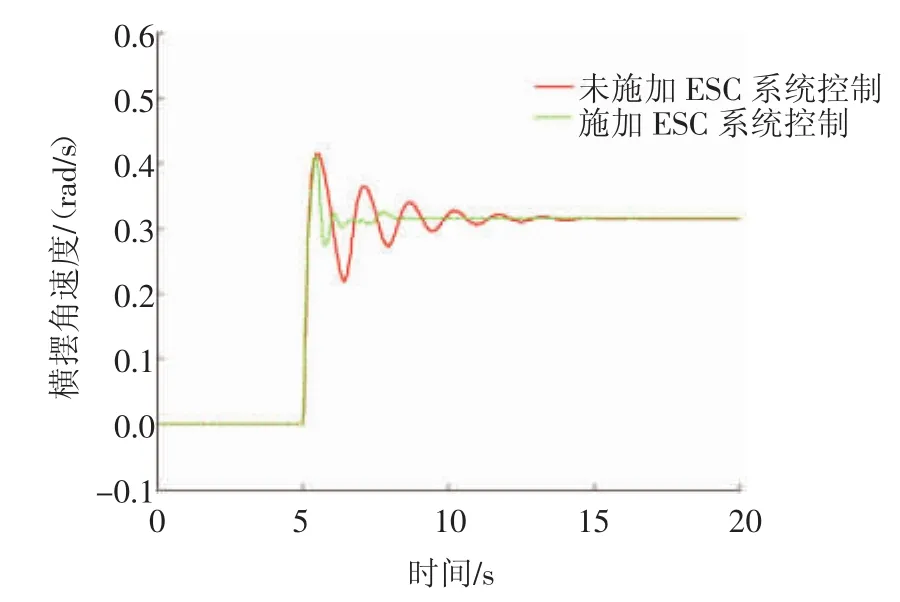
图8 高速大转向工况下汽车横摆角速度变化曲线

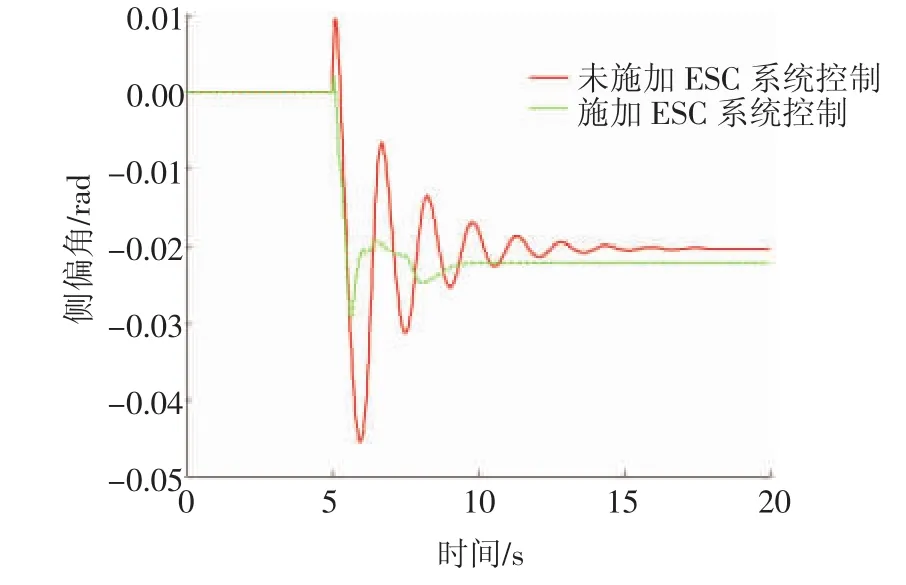
图9 高速大转向工况下汽车质心侧偏角变化曲线

通过以上分析可知，未施加ESC系统控制的汽车在上述极限工况下其横摆角速度和质心侧偏角均有较大的波动且变化更加剧烈，汽车的稳定性和安全性较差。施加ESC系统控制可以有效地减小汽车横摆角速度和质心侧偏角的波动程度以及降低两者的幅值，保证汽车良好的轨迹跟踪能力，进而提高行车的稳定性和安全性。

4 结论

针对极限工况下的纯电动汽车，设计了汽车ESC的PID控制器，结合2种极限工况对施加ESC系统控制前后的汽车进行对比仿真，蛇形试验工况和高速大转向工况这2种极限工况下，施加ESC系统控制后，纯电动汽车的横摆角速度及质心侧偏角均有所减小，仿真结果验证了纯电动汽车ESC系统控制方法的有效性。说明施加ESC系统控制可以有效地减小纯电动汽车横摆角速度及质心侧偏角瞬态响应的超调量，缩短其横摆角速度和质心侧偏角达到稳定状态所需的时间，提高了纯电动汽车的操纵稳定性及行驶安全性。