吊钩梯形圆螺纹有限元分析

赵 波 张中华

(徐工机械建设机械分公司 江苏 徐州 221002)



吊钩梯形圆螺纹有限元分析

赵 波 张中华

(徐工机械建设机械分公司 江苏 徐州 221002)

对履带起重机吊钩螺纹联接部位建立了符合实际情况的三维模型,进行了三维有限元分析,研究了吊钩螺纹联接部位的应力状态和变形情况,并对吊钩螺纹联接部位进行了工作强度的校核，为吊钩的结构设计提供了有价值的理论依据。

吊钩；梯形圆螺纹；有限元；履带起重机

一、引言

吊钩作为起重机在工作时的主承载部件，其设计质量的好坏直接影响着起重机的安全性能和可靠性指标，因此吊钩的设计在起重机的设计当中非常重要[1]。吊钩主要依靠螺纹联接来传递载荷，其联接结构为整个吊钩结构薄弱部位，联接可靠性直接影响到整机的安全可靠性，对于保证功能的实现至关重要。尤其是大吨位的吊钩，为满足相对应的承载要求，螺纹尺寸设计规格比较大，安全系数高，造成了吊钩结构的自重很大，对吊钩整体结构的经济、性能指标都是不利的。如何精确地得到吊钩螺纹联接部位的最大应力分布,对其结构的改进设计具有重要的理论意义。

基于ANSYS有限元分析软件以某履带起重机产品100吨吊钩为例建立了螺纹联接部位的三维有限元模型,进行了静力学分析,得出最大应力分布，并进行了强度校核。

二、吊钩结构介绍

吊钩一般是由钩头1、横梁2、螺母3、轴承4、滑轮架5、滑轮总成6等主要结构组成。如图1、图2所示。其中螺母与钩头通过梯形螺纹联接，是研究的区域。若吊钩钩头承载载荷后，通过钩头上部螺纹传递载荷到螺母上，再通过轴承将载荷传递到横梁上，最后通过滑轮架传递给滑轮总成。吊钩承载载荷比较大，螺纹一般采用梯形圆螺纹。

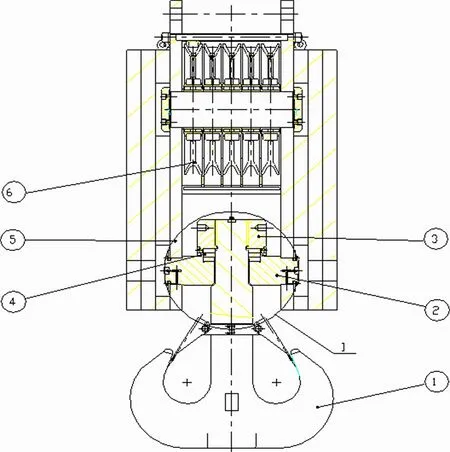
图1 吊钩剖视图

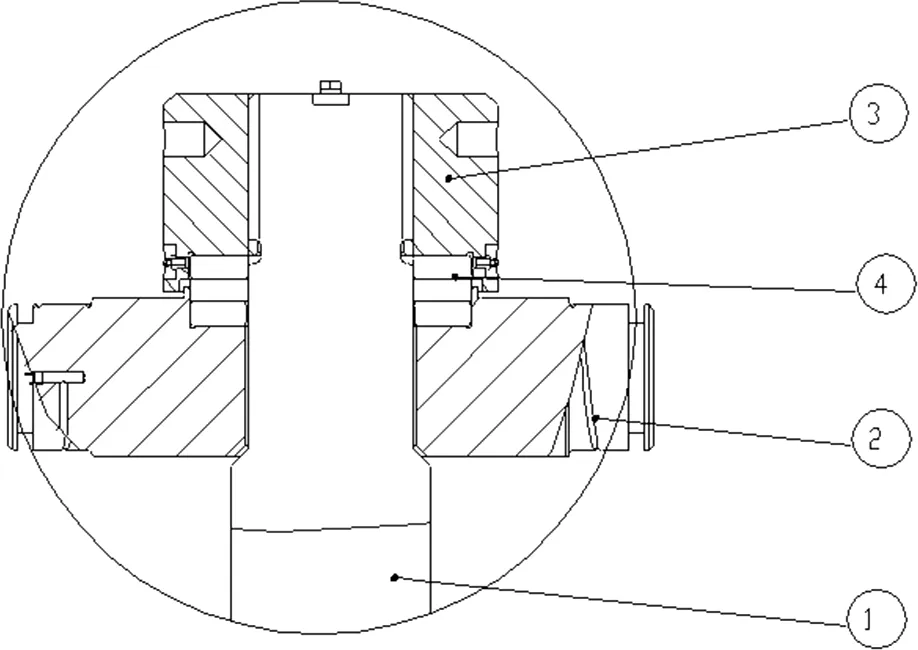
图2 吊钩螺纹区域局部放大视图

三、数学模型理论

若吊钩承载力小，在计算吊钩计算时，一般采用经验公式计算螺纹承载。螺纹副应力分布的研究方法主要包括第一圈承载简化法、均值假设简化法以及指数假设简化法。

(一)第一圈承载简化法——起重机设计标准规定的简化计算方法。假定第一圈螺纹承受有效载荷的一半，剪切面的高度为螺距的一半，校核螺纹牙强度[2]。

(二)均值假设简化法——均匀载荷假设的简单计算方法。假设各圈螺纹受力相等，则每圈承受载荷为F/n，校核螺纹牙的强度[3]。

(三)指数假设简化法。假设螺纹承受指数载荷分布，第一圈螺纹承载载荷的F/2，第二圈承受载荷的F/4，第三圈承受载荷的F/8…………第n圈承受载荷的F/2n[4].

前三种理论简化计算偏安全，忽略了螺纹的弯曲应力，忽略了摩擦系数对载荷分布的影响，本文基于接触理论对螺纹承载进有限元分析计算。

四、吊钩螺纹有限元模型建立

(一)建立几何模型。以某吨位履带起重机用100吨吊钩为例，设计为TY110x12梯形圆螺纹，H=1.866P，简化螺纹的截面图。本文即采用CAD软件Pro/E建立几何模型,它比实物仅简化了一些圆孔倒角及钩头部分等对计算结果影响较小的因素。

(二)建立有限元模型。本文基于ANSYS软件对吊钩螺纹联接部位进行建模，建立三维模型，采用接触分析法对钩头螺纹联接部位的进行有限元计算。螺纹联接结构的实体模型以及有限元模型如图3，图4。该有限元单元类型包括solid45、solid186两种实体单元。

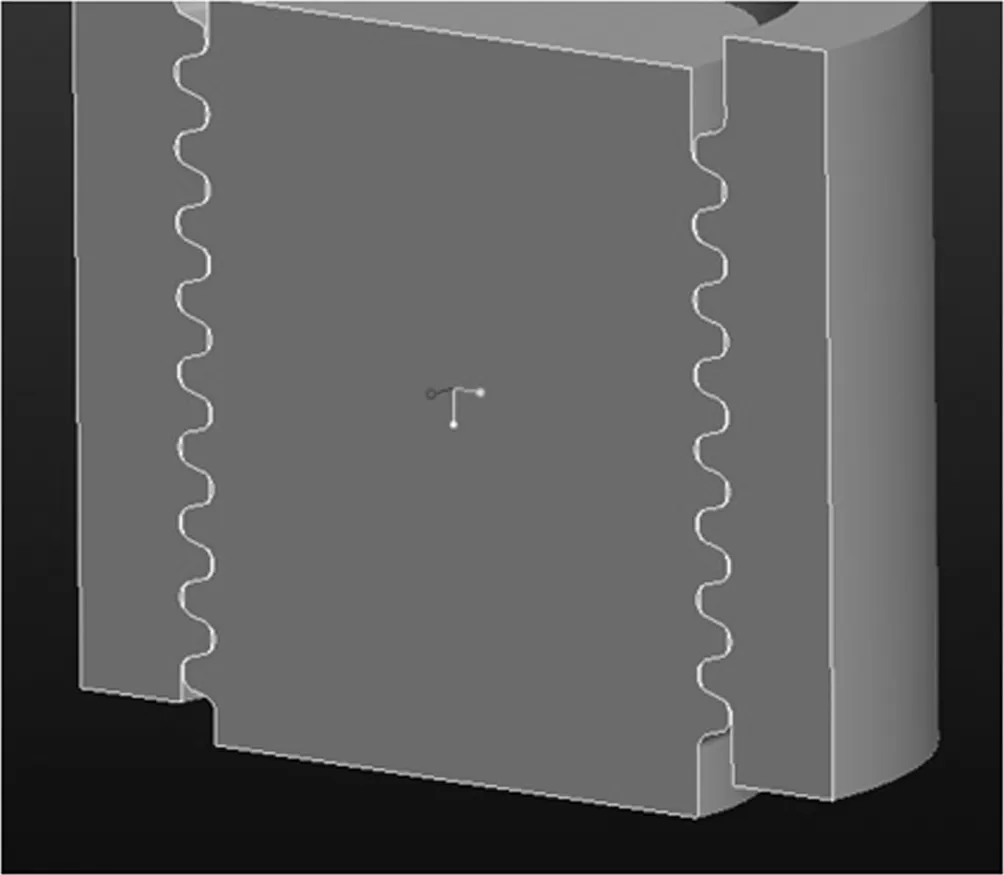
图3 螺纹部分三维简化图

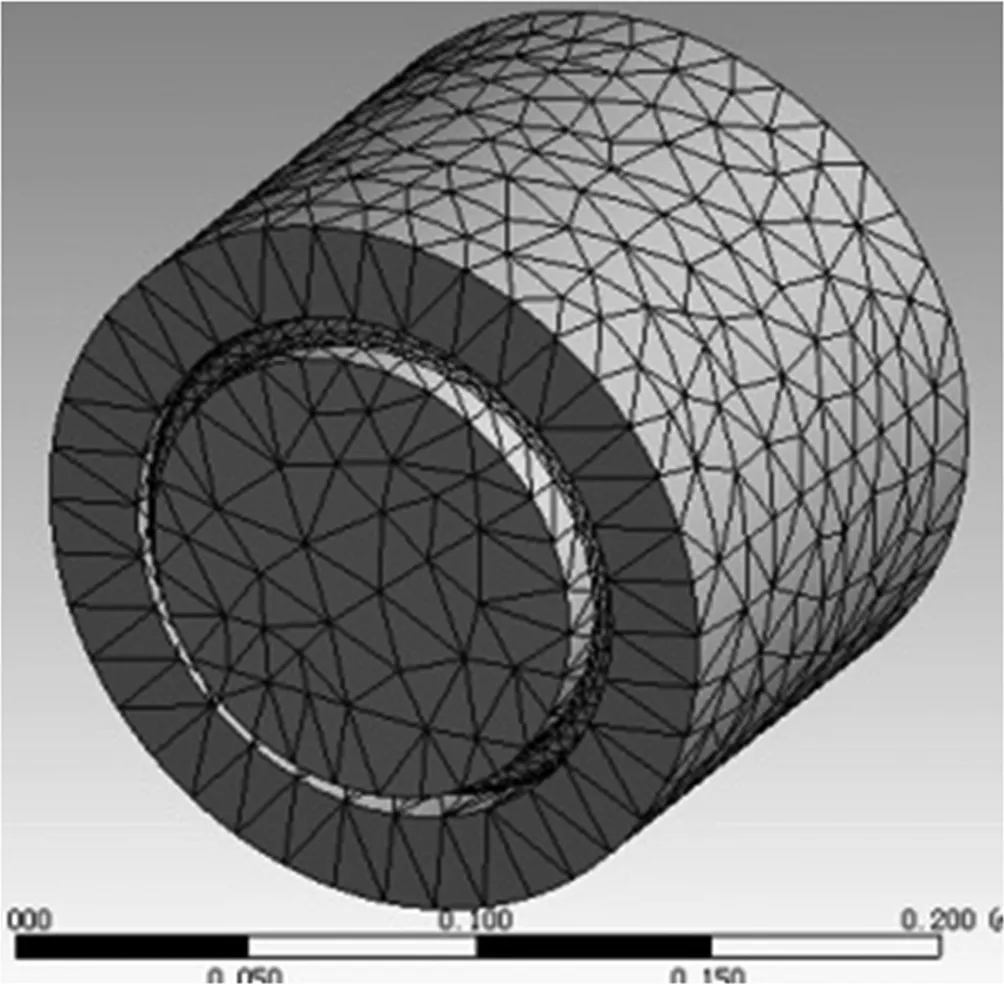
图4 螺纹部分有限元模型图

(三)边界条件与载荷。TY110x12梯形圆螺纹吊钩承受100吨载荷，虑到动载荷系数，按照1.25承载系数计算。螺旋副承受轴向载荷125吨，摩擦因子μ=0.1，啮合数N=8。

五、模拟结果对比分析

(一)螺栓的应力应变分析

吊钩螺纹材料为34Cr2Ni2Mo,屈服强度σs为700 MPa，强度极限σb为1000 MPa。

螺纹副在工作时最危险点发生在第一螺纹根部,存在着应力集中现象，最大主应力σmax=628MPa,应力小于螺纹材料的屈服极限σs=700MPa,满足校核要求。最大剪切应力Τmax=280MPa，剪切强度满足要求。

钩头螺纹处应力分布，可以提取螺纹牙最大等效应力和最大剪切应力，如同所示，各圈螺纹最大等效应力和最大剪切应力成递减方式下降，前三圈递减较快，第6圈,、第7圈及第6圈递减较小，趋向平稳，且最大应力较小，可见螺纹圈数有优化的空间。

(二)计算结果对比

理论计算及有限元计算结果汇总见表1，有限元计算方法可见计算弯曲应力，显示弯曲应力对螺纹牙应力影响，计算更全面。

表1 结果汇总

六、结论

针对本文所作的有限元计算工作，可得到以下几点有益的结论：

1.建立吊钩螺旋副的有限元模型，由分析结果可知，螺纹处最大等效应力随圈增大而递减。

2.梯形螺纹根部应力集中由轴向载荷和局部弯曲载荷共同作用所致。

3.研究表明，螺纹圈数及吊钩的材料有进一步的优化空间。

[1]陈昱璇.基于静强度和疲劳强度的起重机吊钩分析与研究[D]太原科技大学2015

[2]GB/T10051.1-2010,起重吊钩[S].北京：中国标准出版社,2011.

[3]钱学毅等.滑动螺旋副螺纹牙根应力有限元分析[J].北京：机械设计与制造,2006.

[4]吴宗泽 机械设计[M]北京： 高等教育出版社 2001