天山云杉立地指数地统计空间分析

轩俊伟,朱 静

(1.新疆农业大学 草业与环境科学学院,乌鲁木齐 830052；2.新疆农业大学 计算机与信息工程学院,乌鲁木齐 830052)

天山云杉立地指数地统计空间分析

轩俊伟1,朱 静2

(1.新疆农业大学 草业与环境科学学院,乌鲁木齐 830052；2.新疆农业大学 计算机与信息工程学院,乌鲁木齐 830052)

以天山中部新疆农业大学实习林场为研究区,基于实测的天山云杉立地指数数据,利用地统计理论从最优变异函数模型拟合、空间格局分析、克里金插值等方面对天山云杉立地指数进行了研究分析。结果表明：研究区天山云杉立地指数频率分布符合正态分布,在空间上表现出各项同性和一定的空间自相关性,其最优变异函数理论模型为球形模型；利用普通克里金法对天山云杉立地指数进行空间插值的结果优于反权距离加权法,同时还可生成估测标准差分布图,为科学决策提供了强有力的工具。地统计理论分析方法在天山云杉的立地质量评价、规划管理等方面有一定的应用价值和潜力。

天山云杉；立地指数；地统计分析；变异函数；空间插值

森林立地是指森林树木所生存的空间以及与之相关的土壤、地形、气候和生物等自然因素的综合[1]。森林立地根据所处的地理位置不同而引起的自然和生物因子间的差异性,可划分成不同的立地类型。这种分类必然涉及到森林立地评价问题。森林立地质量就是在特定的立地上对影响森林生长的物理、生物及人为管理等因素进行定性或定量的综合评价[2-3]。立地质量决定森林生产力和生产潜力的大小,是森林的生产、经营管理以及规划决策的重要依据[4]。森林立地质量评价方法分为直接评定法和间接评定法。直接评价法包括林分蓄积量法、地位指数法、生长截距法；间接评价方法包括多元地位指数法、植被指数法等[5]。其中基于林分生长规律的立地(地位)指数法是应用最广泛、直接和可靠的立地质量评价方法[6-7]。立地指数法首先要根据林分优势木平均高和对应的平均树龄编制地位指数表,然后通过野外调查获取数据,查找地位指数表得到相应的森林立地指数。这种大范围的立地指数的野外样点数据调查需要付出大量的人力、物力和财力,因此目前的立地指数评价多是以抽样的方式,采集离散的点样方数据对森林立地指数的总体进行简单的估值。

地统计学是由法国统计学家创建的不同于经典统计学的统计学新分支,最先应用于采矿和地质学领域,现今已经广泛应用于土壤、气候、生态、环境、公共卫生等领域[8]。地统计学基于区域化变量理论,运用变异函数工具,对空间离散的样点数据进行无偏最优线性估值,得到空间上连续面域数据[9]。地统计学为利用有限样点数据进行大面积森林立地指数估值提供了强有力的工具。目前,已有了少量利用地统计方法进行森林立地指数估值方面的研究。曾春阳等[10]以杉木人工林为研究对象,利用地统计空间插值法和地理信息技术对杉木立地指数进行了估值,获得了良好的精度。刘永霞等[11]则基于地统计插值方法对马尾松立地指数进行了估值分析,发现其估计值具有无偏和最小方差的特征。这些研究表明了地统计学在森林立地指数估值和空间分析方面有一定的应用价值和潜力。

天山云杉(Piceaschrenkiana)仅在我国天山山脉有分布,是新疆山地森林中最重要的树种[12]。天山云杉起着涵养水源、水土保持、维系山地生态系统等重要生态功能,对天山北坡经济带的可持续发展也有着重要的意义[13]。但目前有关天山云杉立地指数方面的研究偏少,且年代较为久远[14]。特别是利用地统计理论进行天山云杉立地指数估测的研究还未见报道。基于此,本文以天山中部新疆农业大学实习林场为研究区,基于实测的天山云杉立地指数数据,利用地统计克里金法为工具,确定最优变异函数模型、最佳参数对天山云杉立地指数进行空间插值。以期为后续天山云杉立地指数地统计估值最佳模型及参数的选择提供参考,也为天山云杉的保护和管理提供科学的决策依据。

1 材料和方法

1.1 数据采集与处理

研究区位于天山山脉中段的新疆农业大学南山实习林场,天山云杉种群占绝对优势。2016年9月在实习林场金涝坝管护区内,设置了206个临时标准样地,在每个临时标准样地选测3棵天山云杉优势木的树高和树龄,并求取平均值作为平均优势木树高和树龄[1]。将调查结果,按照龄阶分组并统计组内优势木平均树高和树龄标准差,剔除组内3倍树高标准差范围外的异常数据。最终剩余198临时标准样地,然后重新计算各龄阶内优势木平均树高和树龄,用来导向曲线的拟合。平均优势木高生长导向曲线是计算立地指数的基础,通过比较常用的拟合曲线数学模型的拟合精度,最终选用拟合度最高的对数曲线模型。天山云杉基准年龄根据相关研究[14]设为50年。根据拟合公式和基准年龄得出研究区天山云杉立地指数计算公式。利用天山云杉立地指数计算公式即可导出标准样地的立地指数值。

1.2 地统计方法

克里金法是地统计学的主要内容,是将地统计理论应用于解决实际生产问题的方法工具[15]。克里金法是根据已知样点对未知样点进行估计的最优线性无偏估计(Best Linear Unbaised Estimator,BLUE)方法[16]。其本质是对已知样点进行线性加权来估计未知点的值。而权重的确定是该方法的核心,需要在无偏和最优这两个限定前提下进行权重值的求解。无偏是指未知点的估计值期望与实际值的期望要相等。最优则指估计值与实际值的方差最小。而变异函数是克里金法的加权权重的基础。

变异函数是地统计学的主要工具,用来刻画区域化变量的结构性和随机性[17]。区域化变量Z(x)在点x和(x+h)处值增量的方差,在二阶平稳假设下,变异函数计算见公式(1)。半变异函数一般需要利用已知数据进行拟合计算得到,称为实验半变异函数或样本半变异函数。

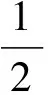
(1)

式中：r表示变异函数值；h为距离；Var表示方差。

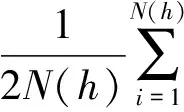
(2)

式中：r*(h)为实验半变异函数；N(h)为样点对数。

依据公式(2)只能计算出有限的变异函数值,为了推断整体区域的变异函数曲线。需要对实验变异函数值进行理论模型曲线拟合,常见的变异函数理论模型有球形模型、高斯模型和指数模型。理论变异函数模型的选择以及参数拟合是影响克里金估值精度的重要因素,一般通过对各模型进行多次选择尝试,最终根据交叉验证精度来确定最优的理论模型。

2 结果与分析

2.1 统计描述

了解待插值样点数据的统计特征是合理、正确进行地统计分析的前提,一般包括查找异常值、数据变换及频率分布检验等内容。样点异常值影响到克里金插值的精度,因此本文利用3倍标准差方法并结合经验知识,剔除掉采样数据中明显错误样地,并对天山云杉样地立地指数进行描述性统计分析。由表1可知,研究区内天山云杉立地指数最大值是最小值的2.7倍,变异系数也大于15%,说明存在较大的空间变异性。偏度和峰度是定量描述变量频率分布形态的指标,偏度系数接近于0,表明立地指数分布曲线呈现对称性。峰度值接近正态分布峰度值3,也表明其频率分布形态特征与正态分布相吻合。K-S检验结果(显著性水平0.89大于0.05)也证实样地立地指数符合正态分布。

表1 天山云杉样地立地指数统计

2.2 变异函数模型拟合

理论变异函数模型及其参数拟合是地统计分析的核心,对最终估值精度有着重要的影响。本文以交叉验证作为评价方法,分别用高斯模型、球形模型、指数模型、K-Bessel模型等理论变异函数模型对天山云杉立地指数进行拟合(表2)。平均误差、平均标准误差、均方根误差等统计指标是选择最优模型依据,一般来说平均误差越接近0、平均标准误差越接近均方根误差、均方根标准误差越接近1,交叉验证精度较好,模型拟合最优[18]。由表2可知,球形模型平均标准误差最接近0、均方根标准误差也最接近1、平均标准误差和均方根误差也比较接近,因此天山云杉立地指数最佳变异函数理论模型选择球形模型。

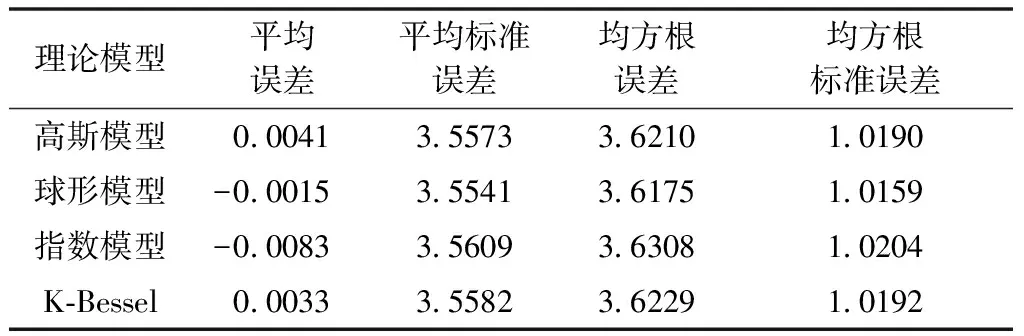
表2 理论变异函数拟合及交叉验证诊断

区域化变量在空间不同方向上还会表现出程度不同的变异性,会影响到克里金估值计算。为探索天山云杉立地指数是否存在各向异性,需要分别计算不同方向上变异函数拟合参数作对比分析。以正北方向为0°,顺时针分别在0°,45°,90°,135°等4个方向上对天山云杉立地指数进行变异函数拟合,结果如表3所示。在4个方向上天山云杉变异函数拟合参数块金值、偏基台值、变程值变化不大,表明在空间上不存在明显的各向异性。因此在各向同性的基础上对天山云杉立地指数变异函数进行拟合,结果得到变异函数块金值为7.10 、偏基台值4.19 、基台值(块金值与偏基台值之和)为11.29、块基比(块金值与基台值之比)为62.89%。块金值度量的是区域化变量的随机性,偏基台值度量的是其空间自相关性,块基比表示空间相关度,其值越大表示变量随机性变异越大、自相关性较弱[19]。块基比值在25%75%之间,则认为该区域化变量属于中等空间自相关性,因此研究区天山云杉立地指数具有中等空间相关性。

表3 不同方向上实验变异函数拟合参数

2.3 克里金插值

在构建理论变异函数的基础上,按照无偏和最小方差的限定条件,对研究区的天山云杉立地指数进行普通克里金估值。由图1可知,实习林场研究区整体天山云杉立地条件较好,研究区中北部、中东部立地指数较高,而南部靠近山脉区域立地指数较小,可能主要受到地形因素的影响。西南部区域由于靠近山脉,冰川融雪产生的径流形成沟谷下切,破坏了天山云杉立地生长条件,所以立地指数较小。

为了对比克里金插值和普通插值方法的差异性,本研究基于相同的样地数据利用反权距离插值方法对天山云杉立地指数进行估测。计算得到反权距离加权插值法交叉验证平均误差为0.053、均方根误差为3.969,普通克里金插值交叉验证平均误差和均方根误差分别为-0.002,3.618。通过对比插值结果,可知反权距离加权插值精度小于普通克里金法。也表明考虑空间结构特征和随机特征的地统计方法能够应用于天山云杉立地指数的估测,并且能够取得较高的精度。

克里金插值法显著不同于其它非地统计插值方法的特点是不仅可以进行估测还可以度量估值结果的不确定性,即可度量估测结果的误差分布情况。由图2可以明显看出,在研究区中部区域及西北部区域克里金估测误差较小,而在研究区西南部、东北部和东南部等边缘地带估值误差明显增大。结合实际样地分布情况,可也看到样地分布集中的区域克里金估值误差较小,没有样地分布的区域克里金估测不确定性大。伴随克里金插值生成的估值标准差分布图,为合理进行决策提供了参考。

图1 普通克里金立地指数插值图

图2 普通克里金插值标准差分布图

3 结论与讨论

3.1 结论

1) 研究区天山云杉立地指数符合正态分布,在空间上表现出各项同性和一定的空间结构性,其最优变异函数理论模型为球形模型。

2) 利用普通克里金法对天山云杉立地指数进行空间插值,结果优于反权距离加权法,同时还可生成估测标准差分布图,地统计理论在天山云杉的保护、管理等方面有一定的应用价值和潜力。

3.2 讨论

地统计分析一般要求样点数据符合正态分布假设,研究区内的实测天山云杉立地指数数据符合正态分布,因此并不需要进行数学变换。最优变异函数模型的选择是地统计估测的核心,涉及到的假设和参数也较多,因此在应用中要保持谨慎。其中各项异性、模型参数拟合和模型精度评价标准是最优变异函数模型选择的重要内容。区域化变量在不同的方向上表现出各异的空间结构的现象称为各项异性。而地统计学是建立在平稳性假设基础之上,在构建变异函数时必须要考虑区域化变量的各项异性问题。本文在4个方向上分别对比分析了天山云杉立地指数的空间变异性,发现在研究区内其表现出各项同性,这就为合理拟合变异函数奠定了基础。变异函数理论模型的选择直接关系到最终克里金估测结果的准确性,一般的方法是从若干常用的变异函数理论模型中选择精度较高的作为最终拟合模型。当前相关研究中,变异函数拟合精度的评价一般分为曲线拟合度和克里金插值交叉验证两类方法。曲线拟合度以变异函数对样点数据的拟合精度高低作为评价标准,交叉验证则以最终估值精度作为评价准则,然而变异函数在数学上的高曲线拟合度并不意味着能真实的反应区域化变量的结构特征,因此本研究选用交叉验证法作为最优变异函数选择的依据。

空间尺度效应是地学研究中的重要内容[20-22],在一种空间尺度下得到的规律是否在其它尺度下也适用,是科学、合理进行决策的前提。本文研究区位于实习林场金涝坝管护区,总面积较小,天山云杉立地指数不仅存在空间自相关性,还存在一定的随机变异性。因此,在小空间尺度上得到的天山云杉立地指数的地统计规律是否在林场及区域等更大的尺度上适用,还有待于深入的研究。

[1]孟宪宇.测树学[M].北京:中国林业出版社,2006.

[2]Skovsgaard J P,Vanclay J K.Forest site productivity:a review of the evolution of dendrometric concepts for even-aged stands[J].Forestry:An International Journal of Forest Research,2008,81(1):13-31.

[3]Waring R H,Milner K S,Jolly W M,et al.Assessment of site index and forest growth capacity across the Pacific and Inland Northwest U.S.A.with a MODIS satellite-derived vegetation index[J].Forest Ecology and Management,2006,228(1-3):285-291.

[4]徐罗,亢新刚,郭韦韦,等.天然云冷杉针阔混交林立地质量评价[J].北京林业大学学报,2016,38(5):11-22.

[5]张志云,蔡学林,欧阳勋志.森林立地研究综述[J].江西农业大学学报,1997,19(6):166-173.

[6]张超,彭道黎,黄国胜,等.基于森林清查数据的三峡库区林地立地质量评价[J].东北林业大学学报,2015,43(11):56-61.

[7]黄国胜,马炜,王雪军,等.基于一类清查数据的福建省立地质量评价技术[J].北京林业大学学报,2014,36(3):1-8.

[8]刘爱丽,王培法,丁园圆.地统计学概论[M].北京:科学出版社,2012.

[9]汤国安,杨昕.ArcGIS地理信息系统空间分析实验教程[M].2版.北京:科学出版社,2012.

[10]曾春阳,唐代生,唐嘉锴.森林立地指数的地统计学空间分析[J].生态学报,2010,30(13):3465-3471.

[11]刘永霞,冯仲科,姚山.基于GIS和地统计学的地位指数估值研究[J].北京林业大学学报,2005,27(S2):88-91.

[12]李明辉,何风华,潘存德.天山云杉天然林不同林层的空间格局和空间关联性[J].生态学报,2011,31(3):620-628.

[13]刘贵峰,丁易,臧润国,等.天山云杉种群分布格局[J].应用生态学报,2011,22(1):9-13.

[14]丁良忱,刘萍.天山中东部雪岭云杉林立地等级表的编制[J].新疆农业科学,1986,(6):25-29.

[15]冯益明.空间统计学理论及其在林业中的应用[M].北京:中国林业出版社,2008.

[16]张仁铎.空间变异理论及应用[M].北京:科学出版社,2005.

[17]Olea R A.A six-step practical approach to semivariogram modeling[J].Stochastic Environmental Research and Risk Assessment,2006,20(5):307-318.

[18]Oliver M A,Webster R.Basic steps in geostatistics:the variogram and kriging[M].London:Springer,2015.

[19]刘祖香,陈效民,靖彦,等.基于地统计学的农田尺度旱地红壤养分空间变异性研究[J].土壤通报,2013,44(2):392-397.

[20]Atkinson P M,Tate N J.Spatial scale problems and geostatistical solutions:a review[J].The Professional Geographer,2000,52(4):607-623.

[21]Swenson N G,Enquist B J,Thompson J,et al.The influence of spatial and size scale on phylogenetic relatedness in tropical forest communities[J].Ecology,2007,88(7):1770-1780.

[22]李霖,应申.空间尺度基础性问题研究[J].武汉大学学报:信息科学版,2005,30(3):199-203.

Geostatistical Analysis ofPiceaSchrenkianaSite Index

XUAN Junwei1,ZHU Jing2

(1.CollegeofGrasslandandEnvironmentalSciences,XinjiangAgriculturalUniversity,Urumqi830052,Xinjiang,China;2.CollegeofComputerandInformationEngineering,XinjiangAgriculturalUniversity,Urumqi830052,Xinjiang,China)

Based on the geo-statistical theory,data of observation samples are used to fit the optimal variation function model and analyze spatial pattern ofPiceaSchrenkiana site index in the forest farm of Xinjiang Agriculture University.The results show that the frequency distribution of the site index ofPiceaSchrenkianagets close to a normal distribution and has moderate degree spatial autocorrelations.After comparing the estimated results with actual results,the spherical models are confirmed with high accuracy.PiceaSchrenkianasite index predictions with the ordinary kriging method are more accurate than those obtained by using inverse distance weighting.Consequently,we identify geostatistical analysis as a promising technique to map complex patterns ofPiceaSchrenkianasite index and suggest that it should be added to the toolbox of forest practitioners.

PiceaSchrenkiana,site index,geostatistical analysis,variogram,spatial interpolation

2017-3-20；

2017-5-10

国家自然科学基金项目(31400543)

轩俊伟(1988-),男,山东聊城人,助教,主要从事GIS空间统计分析方面研究。Email：sd1900@163.com

朱静(1979-),女,广西罗城人,讲师,主要从事机器学习和地统计分析方面研究。Email：zhujin@xjau.edu.cn

S791.18；S714

A

1002-6622(2017)03-0046-05

10.13466/j.cnki.lyzygl.2017.03.010