KU 代数上的(∈,∈∨q(λ,μ))-模糊正关联理想*
2017-08-16廖祖华陈柳红吴树忠朱晓英
李 论,廖祖华,3+,陈柳红,宋 威,吴树忠,朱晓英
1.江南大学 理学院,江苏 无锡 214122
2.江南大学 至善学院,江苏 无锡 214122
3.江南大学 智能系统与网络计算研究所,江苏 无锡 214122
4.江南大学 物联网工程学院,江苏 无锡 214122
KU 代数上的(∈,∈∨q(λ,μ))-模糊正关联理想*
李 论1,2,廖祖华1,2,3+,陈柳红1,2,宋 威4,吴树忠1,朱晓英1
1.江南大学 理学院,江苏 无锡 214122
2.江南大学 至善学院,江苏 无锡 214122
3.江南大学 智能系统与网络计算研究所,江苏 无锡 214122
4.江南大学 物联网工程学院,江苏 无锡 214122
给出了KU代数的点态化(∈,∈∨q(λ,μ))-模糊正关联理想与广义模糊正关联理想的概念,得到了KU代数的(∈,∈∨q(λ,μ))-模糊正关联理想的一些等价刻画,并指出了(∈,∈∨q(λ,μ))-模糊正关联理想有丰富的层次结构;其次得到了多个KU代数的(∈,∈∨q(λ,μ))-模糊正关联理想的交、并、同态像和同态原像(在一定条件下)也是(∈,∈∨q(λ,μ))-模糊正关联理想;而后又对KU代数(∈,∈∨q(λ,μ))-模糊正关联理想的直积以及投影进行了研究;最后给出KU代数的正关联理想的降(升)链条件的新概念,并利用(∈,∈∨q(λ,μ))-模糊正关联理想的性质研究了KU代数的正关联理想的降(升)链条件。
KU代数;(∈,∈∨q(λ,μ))-模糊正关联理想;同态映射;投影;降(升)链条件
1 引言
1965年,Zadeh[1]引入模糊集的概念,它是经典集合的推广,能够表示元素属于它的程度,并被用来描述模糊现象,研究模糊问题。1971年,Rosenfeld[2]将模糊集的概念引入代数学,提出了模糊子群的概念,从而创立了模糊代数学。1981—1993年,Kuroki[3-7]研究了半群的模糊理想、模糊双理想以及模糊半素理想的相关性质。1986年,Swamy等人[8]研究了环的模糊素理想。1980年,刘应明等人[9-10]提出模糊点和模糊集间的“∈”和“q”关系,随后在1992年和1996年,Bhakat等人[11-12]在此基础上给出了(∈,∈∨q)-模糊子群的概念。2011年,Jun等人[13]利用落影理论讨论了BCK代数的模糊正关联理想的性质。2012年,Tebu等人[14]研究了BCI代数的模糊n重正关联理想。2013年,Zulfiqar[15]给出了 BCK 代数的(α,β)-模糊正关联理想的概念,并研究了它的一些基本性质。
2006年,廖祖华等人[16]将“q”关系推广到了“q(λ,μ)”模糊关系,统一了Rosenfeld意义下的模糊代数、Bhakat意义下的(∈,∈∨q)-模糊代数以及-模糊代数,提出了(∈,∈∨q(λ,μ))-模糊代数。之后,他的研究团队在这个方向做了一系列的研究[17-25]。其中,团队成员张建忠等人在文献[19]中提出了N(2,2,0)代数的(∈,∈∨q(λ,μ))-模糊正关联理想的新概念,并研究了它的一系列基本性质。
2009年,受BCK代数及数理逻辑的启发,Prabpayak等人[26-27]通过保留BCK代数中的两条公理(由KU代数的公理系统可以推出x∗x=0)以及添加另外几条公理,提出了KU代数的新概念,并引进了KU代数的理想。KU代数在计算机编码等领域具有潜在的应用价值。在文献[28]中,Rezaei等人证明了KU代数与交换自分配BE代数是等价的,自分配KU代数与Hilbert代数是等价的,并指出了KU代数、BE代数、Hilbert代数、蕴涵代数以及对偶BCK代数之间的关系。而FI代数[29]的公理系统的第2、3、4条也与KU代数公理系统的第1、4条及其性质相类似,格蕴涵代数[30]公理系统中的两条与KU代数公理系统也相类似,于是它们会有一些共同的性质。
2011年,Mostafa等人[31-32]提出了KU代数的模糊理想及直觉模糊理想,并在2014年给出了KU代数的正关联理想[33]的概念。2014年,Gulistan等人[34-35]研究了 KU 代数的(α,β)-模糊理想以及(∈,∈∨qk)-模糊理想的基本性质,Muhiuddin[36]研究了KU代数的双极值模糊理想的基本性质。2016年,Senapati等人[37]研究了KU代数的直觉模糊双正规理想的基本性质。
1921年,Noether[38]提出了环的升链条件。1927年,Artin[39]提出了用降链来区别环。2016年,路腾等人[25]给出了坡代数的-模糊理想的概念,并利用它刻画了坡的滤子的链条件。
以这些研究工作为基础,本文提出了KU代数的(∈,∈∨q(λ,μ))-模糊正关联理想、广义模糊正关联理想的概念和KU代数正关联理想的链条件,并研究了它们的性质。其中,(∈,∈∨q(λ,μ))-模糊正关联理想比其他模糊正关联理想有丰富的层次结构。从例1知,KU 代数的(∈,∈∨q(λ,μ))-模糊正关联理想是(∈,∈)-模糊正关联理想和(∈,∈∨q)-模糊正关联理想的非平凡推广。
本文组织结构如下:第2章给出有关KU代数和模糊集的基础知识;第3章给出KU代数的(∈,∈∨q(λ,μ))-模糊正关联理想的新概念,研究了它的等价刻画、交、并以及偏序等性质;第4章得到了(∈,∈∨q(λ,μ))-模糊正关联理想的同态像和原像(在一定条件下)依然是(∈,∈∨q(λ,μ))-模糊正关联理想的结论;第5章得出(∈,∈∨q(λ,μ))-模糊正关联理想的直积依然是(∈,∈∨q(λ,μ))-模糊正关联理想、(∈,∈∨q(λ,μ))-模糊正关联理想的投影依然是(∈,∈∨q(λ,μ))-模糊正关联理想的结论;第6章用(∈,∈∨q(λ,μ))-模糊正关联理想的性质,对KU代数正关联理想的降(升)链条件进行刻画。
2 预备知识
下面给出有关KU代数及模糊集的基础知识。
首先,给出KU代数及集合的一些基本知识。
定义1[26-27](KU代数)设G是含有常元0的一个非空集合,若在G上定义二元运算“∗”,∀x,y,z∈G,满足下列条件:
(1)(x∗y)∗((y∗z)∗(x∗z))=0;
(2)0∗x=x;
(3)x∗0=0;
(4)若x∗y=0且y∗x=0,则x=y。
称G=(G,∗,0)为KU代数。
由(1)可知,∀x∈G,x∗x=0;∀x,z∈G,z∗(x∗z)=0。
在KU代数G上引入一个二元关系≤,则x≤y的充要条件是y∗x=0。易证,(G;≤)是一个偏序集,0是它最小的元素。
下文不特殊说明,G与G′均表示KU代数。
定义2[33](KU代数的正关联理想)设G是KU代数,A是G的一个非空子集,如果满足下列条件:
(1)0∈A;
(2)∀x,y,z∈G,若z∗(x∗y)∈A,z∗x∈A,有z∗y∈A。则称A是G的一个正关联理想。
定理1[31]设G与G′是两个KU代数,那么在G×G′上规定运算“∗”,∀(x1,x2),(y1,y2)∈G×G′,(x1,x2)∗(y1,y2)=(x1∗y1,x2∗y2),则(G×G′,∗,(0,0′))也是 KU 代数。
定义3[27]设G与G′是KU代数,映射f:G→G′,如果∀x,y∈G,满足:
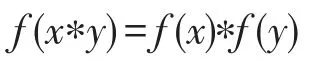
则称f是同态映射。若f是单射,则称f是单同态;若f是满射,则称f是满同态;若f是双射,则称f是同构。
定义4[40](良序集)设集合(S,≤)为一偏序集,≤是其偏序关系,若对任意的S的非空子集,在其序下都有最小元素,则称≤为良序关系,(S,≤)为良序集。
其次,给出模糊集的一些基本知识。
定义5[16](模糊点)若A是G的模糊子集,且
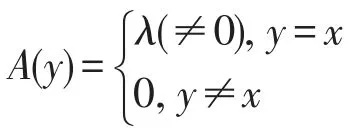
则称A为一个模糊点,记为xλ。
定义6[16]设t,λ,μ∈[0,1],λ<μ,且A是G的模糊子集。若A(x)≥t,则称xt属于A,记作xt∈A。如果t>λ且A(x)+t>2μ,则称模糊点xt广义重于A,记作xtq(λ,μ)A。如果xt∈A或xtq(λ,μ)A,则记作xt∈∨q(λ,μ)A。
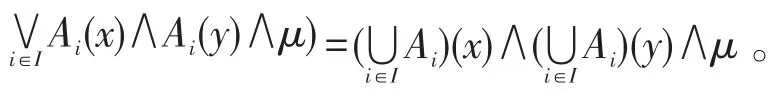
定义7[17](模糊集的直积)设A、B分别是非空集合G、G′的模糊集,定义映射A×B:G×G′→[0,1],(A×B)(x,y)=A(x)∧B(y),∀(x,y)∈G×G′,则A×B是G×G′的模糊子集,并称A×B是A与B的直积。
定义8[17](模糊集的投影)G与G′是两个非空集合,A×B是G×G′的模糊子集,分别定义G、G′的模糊子集为:
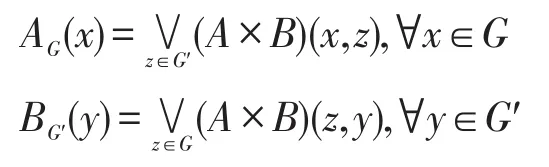
并称AG和BG′分别是A×B在G与G′上的投影。
定义9[41](f-不变性)设G与G′为两个集合,f:G→G′是映射,A是G上的模糊子集,∀x,y∈G,当f(x)=f(y)时,有A(x)=A(y),则称A是关于f-不变的。
定义10[42](扩张原理)设有映射f:X→Y,则由该映射可以诱导出两个如下映射,分别记为f与f-1:
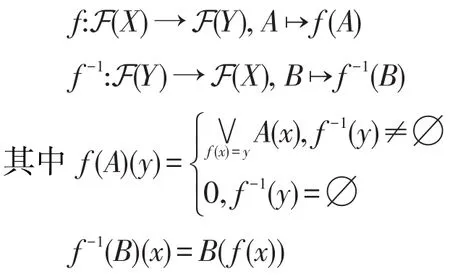
称f(A)是A在f下的像,f-1(B)是B关于f的逆像。
3 (∈,∈∨q(λ,μ))-模糊正关联理想
本节给出 KU 代数的(∈,∈∨q(λ,μ))-模糊正关联理想的新概念,并讨论它的等价刻画及交并等其他基本性质。
KU代数的正关联理想是逻辑推理中假言三段论的一种抽象,而对它的模糊代数结构的研究在控制、信息论及逻辑推理方面有潜在的应用。
定义11设A是KU代数G的一个模糊子集,如果A满足:
(Ⅰ)∀t∈(λ,1],∀x∈G,若xt∈A,有0t∈∨q(λ,μ)A;
(Ⅱ)∀t1,t2∈(λ,1],∀x,y,z∈G,若(z∗(x∗y))t1∈A,(z∗x)t2
∈A,有(z∗y)t1∧t2∈∨q(λ,μ)A。
定义12设A是KU代数G的一个模糊子集,∀x,y,z∈G,如果A满足:
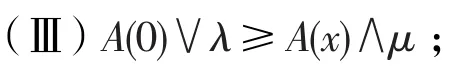
(Ⅳ)A(z∗y)∨λ≥A(z∗(x∗y))∧A(z∗x)∧μ。
则称A是G的广义模糊正关联理想。
下面讨论(∈,∈∨q(λ,μ))-模糊正关联理想、广义模糊正关联理想及模糊集的水平集之间的关系。
定理3设A是G上的模糊子集,则下列条件是等价的:
(1)A是G的(∈,∈∨q(λ,μ))-模糊正关联理想;
(2)A是G的广义模糊正关联理想;
(3)对于任意的t∈(λ,μ],At={x|A(x)≥}t≠∅是G的正关联理想。
以护理学基础教学大纲为依据,通过与教学及临床护理专家研讨,确定临床工作亟须知识及技能,结合贴近临床护理一线工作的理论与实际操作内容,确定教学重点、难点,确定微课作品主题。发放调查问卷,了解对照组护生在护理学基础学习过程中存在的问题及需要加强的知识点,结合护生感性需求,从内容选择、教学活动安排、教学反思等方面设计、制作20节微课,并上传至微信公众平台和校园网络教学平台,供试验组护生观看、学习。
证明(1)⇒(2)
(Ⅰ)⇒(Ⅲ)假设存在x0∈G,使得A(0)∨λ<A(x0)∧μ。令t=A(x0)∧μ,则λ<t≤μ,A(x0)≥t,所以(x0)t∈A。根据定义11知0t∈∨q(λ,μ)A,而A(0)<t≤μ,A(0)+t<t+t≤2μ,矛盾。
(Ⅱ)⇒(Ⅳ)假设∃x0,y0,z0∈G,使得A(z0∗y0)∨λ<A(z0∗(x0∗y0))∧A(z0∗x0)∧μ。取t=A(z0∗(x0∗y0))∧A(z0∗x0))∧μ,则t∈(λ,μ],(z0∗(x0∗y0))t∈A,(z0∗x0)t∈A且(z0∗y0)t∉A,但由(Ⅱ)知(z0∗y0)t∈∨q(λ,μ)A,因此(z0∗y0)tq(λ,μ)A,A(z0∗y0)+t>2μ。A(z0∗y0)>2μ-t≥μ≥t,即(z0∗y0)t∈A,与(z0∗y0)t∉A矛盾,从而(Ⅳ)成立。
(2)⇒(1)
(Ⅲ)⇒(Ⅰ)∀x∈G,∀t∈(λ,1],若xt∈A,则A(x)≥t。因为A是G的广义模糊正关联理想,故A(0)∨λ≥A(x)∧μ≥t∧μ。若t≤μ,因为λ<t,所以A(0)≥t,从而0t∈A;若t>μ,则A(0)∨λ≥μ。因为λ<μ,所以A(0)≥μ。因此A(0)+t≥μ+t>2μ,即0tq(λ,μ)A,从而0t∈∨q(λ,μ)A。
(Ⅳ)⇒(Ⅱ) 若t1,t2∈(λ,1],∀x,y,z∈G,使得(z∗(x∗y))t1,(z∗x)t2∈A,则A(z∗(x∗y))≥t1,A(z∗x)≥t2。又因为A是广义模糊正关联理想,所以A(z∗y)∨λ≥A(z∗(x∗y))∧A(z∗x)∧μ。故A(z∗y)∨λ≥(t1∧t2)∧μ。若(t1∧t2)≤μ,因为λ<t1且λ<t2,所以A(z∗y)≥t1∧t2,即(z∗y)t1∧t2∈A;若(t1∧t2)>μ,则A(z∗y)≥μ。因此A(z∗y)+(t1∧t2)≥μ+(t1∧t2)>2μ,故(z∗y)t1∧t2q(λ,μ)A,从而(z∗y)t1∧t2∈∨q(λ,μ)A。
(2)⇒(3)
∀t∈(λ,μ],若At≠∅,则∃x∈At,A(x)≥t。由(Ⅲ)知,A(0)∨λ≥A(x)∧μ≥t∧μ=t。因为t>λ,所以A(0)≥t,0∈At。又∀z∗(x∗y),z∗x∈At,有A(z∗(x∗y))≥t且A(z∗x)≥t,再由(Ⅳ)知,A(z∗y)∨λ≥A(z∗(x∗y))∧A(z∗x)∧μ≥t∧μ=t。因为t>λ,所以A(z∗y)≥t。故z∗y∈At,从而At是G的一个正关联理想。
(3)⇒(2)
假设存在x∈G,满足A(0)∨λ<A(x)∧μ。令t=A(x)∧μ,则λ<t≤μ,A(x)≥t且A(0)<t,因此x∈At,At≠∅。由已知条件,At是G的正关联理想,所以0∈At,即A(0)≥t。但A(0)<t,矛盾。因此,∀x∈G有A(0)∨λ≥A(x)∧μ。又若∃x,y,z∈G,使得A(z∗y)∨λ<A(z∗(x∗y))∧A(z∗x)∧μ,则取t=A(z∗(x∗y))∧A(z∗x)∧μ。因此t∈(λ,μ],A(z∗(x∗y))∧A(z∗x)≥t 且A(z∗y)<t,从而z∗(x∗y),z∗x∈At。又At是G的正关联 理 想,因 此z∗y∈At,即A(z∗y)≥t。又因为A(z∗y)<t,矛盾,所以∀x,y,z∈G,有A(z∗y)∨λ≥A(z∗(x∗y))∧A(z∗x)∧μ。
综上所述,A是G的广义模糊正关联理想。
当λ=0,μ=1时,可以得到KU代数的(∈,∈)-模糊正关联理想。
推论1设A是G上的模糊子集,下列条件是等价的:
(1)A是G的(∈,∈)-模糊正关联理想;
(2)A(0)≥A(x)且A(z∗y)≥A(z∗(x∗y))∧A(z∗x);
(3)对于任意的t∈(0,1],At={x|A(x)≥t}≠∅ 时是G的正关联理想。
当λ=0,μ=0.5时,可以得到 KU 代数的(∈,∈∨q)-模糊正关联理想。
推论2设A是G上的模糊子集,下列条件是等价的:
(1)A是G的(∈,∈∨q)-模糊正关联理想;
(2)A(0)≥A(x)∧0.5 且A(z∗y)≥A(z∗(x∗y))∧A(z∗x)∧0.5;
(3)对于任意的t∈(0,0.5],非空集合At={x|A(x)≥t}是G的正关联理想。
例1设G={0,1,2,3,4},定义“∗”,运算表如表1,则(G,∗,0 )是KU代数。
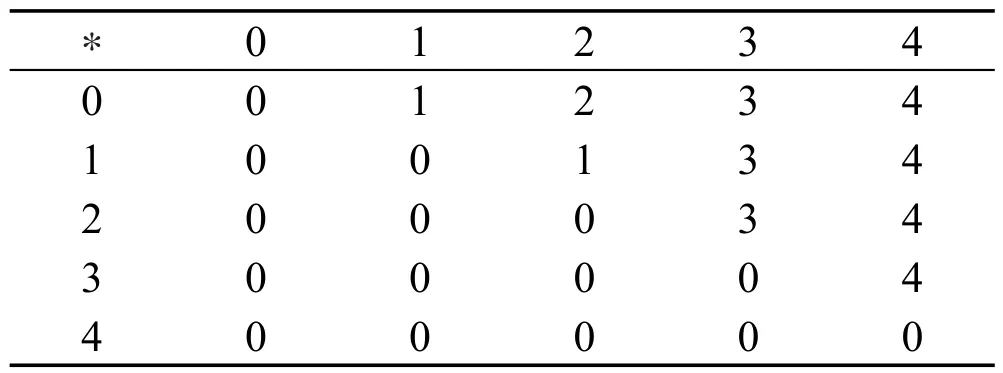
Table1 Operator“∗”表1 运算“∗”
(1)A1:G→[0,1],A1(0)=0.4,A1(1)=0.6,A1(2)=0.6,A1(3)=0.3,A1(4)=0.2,其中λ=0.1<A1(4)<A1(3)<A1(0)=μ<A1(1)=A1(2)<1。可验证A1是G的(∈,∈∨q(λ,μ))-模糊正关联理想。因为A1(0)=0.4<0.5=A1(2)∧0.5,所以A1不是G的(∈,∈∨q)-模糊正关联理想。又因为A1(0)=0.4<0.6=A1(2),所以A1也不是G的(∈,∈)-模糊正关联理想。
(2)A2:G→[0,1],A2(0)=0.5,A2(1)=A2(2)=0.6,A2(3)=0.3,A2(4)=0.2。其中,0<λ<A2(4)<A2(3)<A2(0)=0.5<μ<A2(1)=A2(2)<1,则由定义知A2是G的(∈,∈∨q)-模糊正关联理想。因为A2(0)∨λ=0.5<A2(2)∧μ,所以A2不是G的(∈,∈∨q(λ,μ))-模糊正关联理想。又因为A2(0)=0.5<0.6=A2(1),所以A2也不是G的(∈,∈)-模糊正关联理想。
(3)A3:G→[0,1],A3(0)=0.6,A3(1)=A3(2)=0.4,A3(3)=0.3,A3(4)=0.2。其中,0<λ<A3(4)<A3(3)<A3(2)=A3(1)<μ<A3(0)<1。因此,∀x,y,z∈G,A3是G的(∈,∈)-模糊正关联理想。
由此可知,(∈,∈∨q(λ,μ))-模糊正关联理想是与(∈,∈)-模糊正关联理想及(∈,∈∨q)-模糊正关联理想不同的一种新的模糊代数结构。
定理 4A为G的(∈,∈∨q(λ,μ))-模糊正关联理想的充要条件是∀t∈[λ,μ),当A(t)={x|A(x)>t}≠∅ 时,A(t)为G的正关联理想。
证明必要性:∀t∈[λ,μ),若A(t)非空,则∃x∈A(t),因此A(x)>t。因为A为G的(∈,∈∨q(λ,μ))-模糊正关联理想,所以A(0)∨λ≥A(x)∧μ>t。因为t≥λ,故A(0)>t,所以0∈A(t)。又∀x,y,z∈G,若z∗(x∗y)∈A(t),z∗x∈A(t),因为A为G的(∈,∈∨q(λ,μ))-模糊正关联理想,所以A(z∗y)∨λ≥A(z∗(x∗y))∧A(z∗x)∧μ>t。因为t≥λ,所以A(z∗y)>t,即z∗y∈A(t),故A(t)是G的正关联理想。
充分性:若∃x∈G,使得A(0)∨λ<A(x)∧μ,令t=A(0)∨λ,则t∈[λ,μ)。因此A(x)>t,x∈A(t),A(t)非空。又已知A(t)是G的正关联理想,于是0∈A(t),即A(0)>t。又因为A(0)<t,矛盾。所以∀x∈G,都有A(0)∨λ≥A(x)∧μ。
假设存在x,y,z∈G,使得A(z∗y)∨λ<A(z∗(x∗y))∧A(z∗x)∧μ。令t=A(z∗y)∨λ,则A(z∗x)>t,A(z∗(x∗y))>t,即z∗x,z∗(x∗y)∈A(t)。又A(t)是G的正关联理想,于是z∗y∈A(t),即A(z∗y)>t。又因为A(z∗y)≤t,矛盾。所以∀x,y,z∈G,A(z∗y)∨λ≥A(z∗(x∗y))∧A(z∗x)∧μ。
综上所述,A为G的(∈,∈∨q(λ,μ))-模糊正关联理想。
定理5至定理 7讨论(∈,∈∨q(λ,μ))-模糊正关联理想的层次结构。
定理5A为G的模糊子集,∀t∈(μ,1],∅≠At是G的正关联理想的充要条件是下列两条成立:
(1)A(x)≤A(0)∨μ;
(2)A(z∗(x∗y))∧A(z∗x)≤A(z∗y)∨μ。
证明必要性:若(1)不成立,假设存在x∈G满足A(x)>A(0)∨μ。取t=A(x),则x∈At,t∈(μ,1]。但0∉At,因为At是G的正关联理想,所以0∈At,矛盾。从而∀x∈G,有A(x)≤A(0)∨μ。
若(2)不成立,则∃x,y,z∈G,使得A(z∗(x∗y))∧A(z∗x)>A(z∗y)∨μ。令t=A(z∗(x∗y))∧A(z∗x),则t∈(μ,1],A(z∗(x∗y))≥t,A(z∗x)≥t且A(z∗y)<t,因此z∗(x∗y)∈At且z∗x∈At。因为At是G的正关联理想,所以z∗y∈At,即A(z∗y)≥t,与A(z∗y)<t矛盾。从而∀x,y,z∈G,有A(z∗(x∗y))∧A(z∗x)≤A(z∗y)∨μ。
充分性:∀t∈(μ,1]且∅≠At,则∃x∈At。由(1)知A(x)≤A(0)∨μ,即A(0)∨μ≥t。因为t>μ,所以A(0)≥t,0∈At。又∀x,y,z∈G,若z∗(x∗y)∈At,z∗x∈At,则A(z∗(x∗y))≥t,A(z∗x)≥t。由(2)知A(z∗y)∨μ≥A(z∗(x∗y))∧A(z∗x)≥t,因为t>μ,所以A(z∗y)≥t,即z∗y∈At,从而At是G的正关联理想。
推论3A为G的模糊子集,∀t∈(μ,1],∅≠At是G的正关联理想的充要条件是A是(∈,∈∨q(λ,μ))-模糊正关联理想。
定理6A为G的模糊子集,∀t∈(0,λ],∅≠At是G的正关联理想的充要条件是下列两条成立:
(1)A(x)∧λ≤A(0);
(2)A(z∗(x∗y))∧A(z∗x)∧λ≤A(z∗y)。
证明必要性:若(1)不成立,则存在x∈G使得A(x)∧λ>A(0)。取t=A(x)∧λ,则x∈At,t∈(0,λ]。因为At是G的正关联理想,所以0∈At,A(0)≥t,与A(0)<t矛盾。故∀x∈G,有A(x)∧λ≤A(0)。
若(2)不成立,则∃x,y,z∈G,使得A(z∗(x∗y))∧A(z∗x)∧λ>A(z∗y)。令t=A(z∗(x∗y))∧A(z∗x)∧λ,则t∈(0,λ],A(z∗(x∗y))≥t且A(z∗x)≥t,因此z∗(x∗y),z∗x∈At。因为At是G的正关联理想,所以z∗y∈At。A(z∗y)≥t与A(z∗y)<t,矛盾。故(2)成立。
充分性:∀t∈(0,λ],∅≠At,则∃x∈At,因此A(x)≥t。又由(1)成立,因此A(0)≥A(x)∧λ≥t∧t=t,即0∈At。又∀x,y,z∈G,若z∗(x∗y),z∗x∈At,由(2)知A(z∗y)≥A(z∗(x∗y))∧A(z∗x)∧λ≥t,所以z∗y∈At,从而At是G的正关联理想。
推论4A为G的模糊子集,∀t∈(0,λ],∅≠At是G的正关联理想的充要条件是A是(∈,∈∨q(0,λ))-模糊正关联理想。
由定理3、定理5和定理6得到定理7,它表明(∈,∈∨q(λ,μ))-模糊正关联理想比(∈,∈)-模糊正关联理想和(∈,∈∨q)-模糊正关联理想有更丰富的层次结构。
定理7A是模糊子集,At(t∈(0,1])是A的水平集,则下列结论成立。
(1)∀t∈(0,λ],At≠∅ 是G的正关联理想的充要条件是A是(∈,∈∨q(0,λ))-模糊正关联理想。
(2)∀t∈(λ,μ],At≠∅ 是G的正关联理想的充要条件是A是( ∈, ∈∨q(λ,μ))-模糊正关联理想。
(3)∀t∈(μ,1],At≠∅ 是G的正关联理想的充要条件是A是(∈,∈∨q(μ,1))-模糊正关联理想。
定理8A是G的(∈,∈∨q(λ,μ))-模糊正关联理想,则A(z∗(z∗x))∨λ≥A(z∗x)∧μ。
证明(A(z∗(z∗x))∨λ)∨λ≥(A(z∗(x∗(z∗x)))∧A(z∗x)∧μ)∨λ=(A(z∗0)∧A(z∗x)∧μ)∨λ=(A(0)∧A(z∗x))∨λ=(A(0)∨λ)∧(A(z∗x)∨λ)≥(A(z∗x)∧μ)∧A(z∗x)=A(z∗x)∧μ。
以下两个定理讨论(∈,∈∨q(λ,μ))-模糊正关联理想族的交和并。
定理 9若 {Ai}i∈I是G的(∈,∈∨q(λ,μ))-模糊正关联理想族,则Ai也是G的(∈,∈∨q(λ,μ))-模糊正关联理想。
证明∀x∈G,则(Ai)(0)∨λ=(Ai)(0)∨λ=(Ai(0)∨λ)≥(Ai(x)∧μ)=(Ai(x))∧μ=(Ai)(x)∧μ,因此(Ⅲ)成立。又∀x,y,z∈G,(Ai)(z∗y)∨λ=(Ai(z∗y))∨λ=(Ai(z∗y)∨λ)≥(Ai(z∗(x∗y))∧Ai(z∗x)∧μ)≥(Ai(z∗(x∗y))∧(Ai(z∗x))∧μ=(Ai)(z∗(x∗y))∧Ai)(z∗x)∧μ,因此(Ⅳ)成立。
定理 10如果 {Ai}i∈I是G的(∈,∈∨q(λ,μ))-模糊正关联理想族,并对所有的i,j∈I,Ai⊆Aj或Aj⊆Ai,则Ai也是G的(∈,∈∨q(λ,μ))-模糊正关联理想。
证明∀x∈G,则(Ai)(0)∨λ=(Ai(0))∨λ=(Ai(0)∨λ)≥(Ai(x)∧μ)=(Ai)(x)∧μ,因此(Ⅲ)成立。
定理11设A为G的非空子集,B为G的模糊子集定义如下:
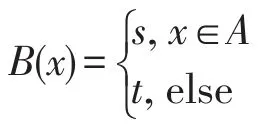
其中t<s,0≤t<μ,λ<s≤1,则B是G的(∈,∈∨q(λ,μ))-模糊正关联理想的充要条件是A是G的正关联理想。
证明∀α∈(λ,μ]
当0≤t≤λ,λ<s<μ时:

根据定理3可知B是G的(∈,∈∨q(λ,μ))-模糊正关联理想。
推论5A是G的正关联理想的充要条件是A的特征函数 χA是G的(∈,∈∨q(λ,μ))-模糊正关联理想。
推论5说明(∈,∈∨q(λ,μ))-模糊正关联理想的定义是合理的。
下面利用G的偏序关系讨论(∈,∈∨q(λ,μ))-模糊正关联理想有关的性质。
定理12设A是G的一个(∈,∈∨q(λ,μ))-模糊正关联理想,如果不等式x∗y≤z在G中成立,那么A(y)∨λ≥A(z)∧A(z∗x)∧μ。
证明若x∗y≤z,则z∗(x∗y)=0。又A(y)∨λ=A(0∗y)∨λ≥A(0∗(z∗y))∧A(0∗z)∧μ=A(z∗y)∧A(z)∧μ,则A(y)∨λ=(A(y)∨λ)∨λ≥(A(z∗y)∧A(z)∧μ)∨λ=(A(z∗y)∨λ)∧(A(z)∨λ)∧(λ∨μ)≥(A(z∗(x∗y))∧A(z∗x)∧μ)∧A(z)∧μ=A(z∗(x∗y))∧A(z∗x)∧A(z)∧μ=A(0)∧A(z∗x)∧A(z)∧μ。
从而A(y)∨λ=(A(y)∨λ)∨λ≥(A(0)∧A(z∗x)∧A(z)∧μ)∨λ=(A(0)∨λ)∧(A(z∗x)∨λ)∧(A(z)∨λ)∧(λ∨μ)≥A(z∗x)∧μ∧A(z∗x)∧A(z)∧μ=A(z)∧A(z∗x)∧μ。
定理13设A是G的一个(∈,∈∨q(λ,μ))-模糊正关联理想,如果y≤x,那么A(y)∨λ≥A(x)∧μ。
证明若y≤x,则x∗y=0,因此A(y)∨λ=(A(0∗y)∨λ)∨λ≥(A(0∗(x∗y))∧A(0∗x)∧μ)∨λ=(A(0∗0)∧A(x)∧μ)∨λ=(A(0)∨λ)∧((A(x)∧μ)∨λ)≥(A(x)∧μ)∧((A(x)∧μ)∨λ)≥A(x)∧μ。
4 (∈,∈∨q(λ,μ))-模糊正关联理想的像与原像
下面给出(∈,∈∨q(λ,μ))-模糊正关联理想的同态像与原像的性质。
定理14设f是G到G′的同态,B是G′的(∈,∈∨q(λ,μ))-模糊正 关 联理想,则 f-1(B)是G的(∈,∈∨q(λ,μ))-模糊正关联理想。
证明先证明f-1(B)满足(Ⅰ)。∀t∈(λ,1],∀x∈G,若xt∈f-1(B),有f-1(B)(x)=B(f(x))≥t,即(f(x))t∈B。因为B是G′的(∈,∈∨q(λ,μ))-模糊正关联理想,所以(0′)t∈∨q(λ,μ)B。又因为f是G到G′的同态,所以f(0)=f(0 ∗0)=f(0)∗f(0)=0′。若(0′)t∈B,则B(0′)≥t,那么f-1(B)(0)=B(f(0))=B(0′)≥t,从而0t∈f-1(B)。若(0′)tq(λ,μ)B,则f-1(B)(0)+t=B(f(0))+t=B(0′)+t>2μ,于是0tq(λ,μ)f-1(B),从而0t∈∨q(λ,μ)f-1(B)。
再证f-1(B)满足(Ⅱ)。∀t1,t2∈(λ,1],∀x,y,z∈G,若(z∗x)t1
∈f-1(B),(z∗(x∗y))t2∈f-1(B),则B(f(z)∗f(x))=B(f(z∗x))=f-1(B)(z∗x)≥t1,B(f(z)∗(f(x)∗f(y)))=B(f(z∗(x∗y)))=f-1(B)(z∗(x∗y))≥t2,因此(f(z)∗f(x))t1∈B,(f(z)∗(f(x)∗f(y)))t2∈B。又因为B是G′的(∈,∈∨q(λ,μ))-模糊正关联理想,所以(f(z)∗f(y))t1∧t2∈∨q(λ,μ)B。若(f(z)∗f(y))t1∧t2∈B,则f-1(B)(z∗y)=B(f(z∗y))=B(f(z)∗f(y))≥t1∧t2,从而(z∗y)t1∧t2∈f-1(B);若(f(z)∗f(y))t1∧t2q(λ,μ)B,则 f-1(B)(z∗y)+t1∧t2=B(f(z∗y))+t1∧t2=B(f(z)∗f(y))+t1∧t2>2μ,因此(z∗y)t1∧t2q(λ,μ)f-1(B)。从而(z∗y)t1∧t2∈∨q(λ,μ)f-1(B)。
综上所述f-1(B)是G的(∈,∈∨q(λ,μ))-模糊正关联理想。
定理15A是G的模糊子集,f是G到G′的同态,且A是f-不变的。若f(A)是G′的(∈,∈∨q(λ,μ))-模糊正关联理想,则A是G的(∈,∈∨q(λ,μ))-模糊正关联理想。
证明(1)∀t∈(λ,1],∀x∈G,若xt∈A,则A(x)≥t。令y=f(x),因为A是f-不变的,所以f(A)(y)=A(w)=A(x)≥t,即yt∈f(A)。又因为f(A)是G′的(∈,∈∨q(λ,μ))-模糊正关联理想,所以0′t∈∨q(λ,μ)f(A)。若0′t∈f(A),即f(A)(0′)≥t,则(0′)≥t,即0t∈A。若0′tq(λ,μ)f(A),则t=f(A)(0′)+t>2μ。因此,0t∈∨q(λ,μ)A。
(2)∀x,y,z∈G,∀t1,t2∈(λ,1],若(z∗(x∗y))t1∈A,(z∗x)t2∈A,则A(z∗(x∗y))≥t1,A(z∗x)≥t2。令f(x)=x′,f(y)=y′,f(z)=z′。因为f 是同态映射,则f(z∗y)=f(z)∗f(y)=z′∗y′且f(z∗(x∗y))=z′∗(x′∗y′),又因为A是f-不变的,所以(x′∗y′)),。因此(z′∗(x′∗y′))t1∈f(A) 且(z′∗x′)t2∈f(A)。而f(A)是G′的(∈,∈∨q(λ,μ))-模糊正关联理想,于是(z′∗y′)t1∧t2∈∨q(λ,μ)f(A),即(z′∗y′)t1∧t2∈f(A) 或(z′∗y′)t1∧t2q(λ,μ)f(A),因 此,或。从而(z∗y)t1∧t2∈∨q(λ,μ)A。
综上所述,A是G的(∈,∈∨q(λ,μ))-模糊正关联理想。
定理16设f是G到G′的满同态,且A是f-不变的,则A是G的(∈,∈∨q(λ,μ))-模糊正关联理想的充要条件是f(A)是G′的(∈,∈∨q(λ,μ))-模糊正关联理想。
证明必要性:(1)∀y∈G′,∀t∈(λ,1]。因为f是满射,所以∃x0∈G使得f(x0)=y。若yt∈f(A),则t≤f(A)(y)=A(x)=A(x0),从而(x0)t∈A。因为A是G的(∈,∈∨q(λ,μ))-模糊正关联理想,所以若0t∈A,即A(0)≥t,则f(A)(0′)=A(x)≥A(0)≥t,从而(0′)t∈f(A)。若0tq(λ,μ)A,则 f(A)(0′)+t=A(x)+t=A(0)+t>2μ,故(0′)t∈∨q(λ,μ)f(A)。
(2)∀x′,y′,z′∈G,∀t1,t2∈(λ,1],因为f 是满同态,所以∃x,y,z∈G,使得f(x)=x′,f(y)=y′,f(z)=z′,且f(z∗(x∗y))=z′∗(x′∗y′)。若(z′∗(x′∗y′))t1∈f(A),(z′∗x′)t2
∈A。因为A是G的(∈,∈∨q(λ,μ))-模糊正关联理想,所以(z∗y)t1∧t2
∈∨q(λ,μ)A。f(A)(z′∗y′)=A(w)=A(z∗y)≥t1∧t2,或者f(A)(z′∗y′)+t1∧t2=A(w)+t1∧t2=A(z∗y)+t1∧t2>2μ。故(z′∗y′)t1∧t2∈∨q(λ,μ)f(A)。从而f(A)是G′的(∈,∈∨q(λ,μ))-模糊正关联理想。
充分性:由定理15的结论可得。
5 (∈,∈∨q(λ,μ))-模糊正关联理想的直积与投影
下面给出(∈,∈∨q(λ,μ))-模糊正关联理想的直积及投影的性质。
定理17如果A、B分别是KU代数G与G′的(∈,∈∨q(λ,μ))-模糊正关联理想,则直积A×B是 G×G′的(∈,∈∨q(λ,μ))-模糊正关联理想。
证明因为A、B分别是 KU代数G与G′的(∈,∈∨q(λ,μ))-模糊正关联理想,所以A、B分别是 KU代数G与G′的广义模糊正关联理想。于是∀(x,y)∈G×G′,其中x∈G,y∈G′,有(A×B)(0,0)∨λ=(A(0)∧B(0))∨λ=(A(0)∨λ)∧(B(0)∨λ)≥(A(x)∧μ)∧(B(y)∧μ)=A(x)∧B(y)∧μ=(A×B)(x,y)∧μ。又∀(x1,x2),(y1,y2),(z1,z2)∈G×G′,其中x1,y1,z1∈G,x2,y2,z2∈G′,则:
(A×B)((z1,z2)∗(y1,y2))∨λ=(A×B)(z1∗y1,z2∗y2)∨λ=(A(z1∗y1)∧B(z2∗y2))∨λ=(A(z1∗y1)∨λ)∧(B(z2∗y2)∨λ)≥(A(z1∗(x1∗y1))∧A(z1∗x1)∧μ)∧(B(z2∗(x2∗y2))∧B(z2∗x2)∧μ)=(A(z1∗(x1∗y1))∧B(z2∗(x2∗y2)))∧(A(z1∗x1)∧B(z2∗x2))∧μ=(A×B)(z1∗(x1∗y1),z2∗(x2∗y2))∧(A×B)(z1∗x1,z2∗x2)∧μ=(A×B)((z1,z2)∗((x1,x2)∗(y1,y2)))∧(A×B)((z1,z2)∗(x1,x2))∧μ
综上,A×B是G×G′的(∈,∈∨q(λ,μ))-模糊正关联理想。
定理18如果A×B是 G×G′的(∈,∈∨q(λ,μ))-模糊正关联理想,则AG是G的(∈,∈∨q(λ,μ))-模糊正关联理想,BG′是G′的(∈,∈∨q(λ,μ))-模糊正关联理想。
证明因为A×B是G×G′的(∈,∈∨q(λ,μ))-模糊正关联理想,由定理3知,A×B是G×G′的广义模糊正关联理想。
(1)∀x∈G,AG(0)∨λ=((A×B)(0,z))∨λ=((A(0)∧B(z))∨λ=(((A(0)∨λ)∧(B(z)∨λ))≥((A(x)∧μ)∧B(z))=(A(x)∧B(z))∧μ=((A×B)(x,z))∧μ=AG(x)∧μ。
(2)又∀x,y,z∈G,AG(z∗y)∨λ=((A×B)(z∗y,w))∨λ∨λ=((A×B)(z∗y,w)∨λ)∨λ≥((A×B)(z∗y,0′)∨λ)∨λ=((A×B)((z,0′)∗(y,0′))∨λ)∨λ≥[(A×B)((z,0′)∗((x,w1)∗(y,0′)))∧(A×B)((z,0′)∗(x,w1))∧μ]∨λ=((A×B)(z∗(x∗y),0′)∧(A×B)(z∗x,w1)∧μ)∨ λ=((A(z∗(x∗y))∧B(0′))∧((A×B)(z∗x,w1)∧μ))∨λ=(A(z∗(x∗y))∨λ)∧((B(0′)∨λ)∧((A×B)(z∗x,w1)∧μ)∨ λ) ≥A(z∗(x∗y))∧(B(w2)∧μ)∧((A×B)(z∗x,w1)∧μ)=((A×B)(z∗(x∗y),w2)∧(A×B)(z∗x,w1)∧μ。
由w2的任意性,得AG(z∗y)∨λ≥((A×B)(z∗(x∗y),w2)∧(A×B)(z∗x,w1)∧μ)=((A×B)(z∗(x∗y),w2))∧(A×B)(z∗x,w1)∧μ=AG(z∗(x∗y))∧(A×B)(z∗x,w1)∧μ。
再由w1的任意性,得AG(z∗y)∨λ≥(AG(z∗(x∗y))∧(A×B)(z∗x,w1)∧μ)=AG(z∗(x∗y))∧((A×B)(z∗x,w1))∧μ=AG(z∗(x∗y))∧AG(z∗x)∧μ。
综合(1)和(2)知,AG是G的(∈,∈∨q(λ,μ))-模糊正关联理想。
同理可证BG′是G′的(∈,∈∨q(λ,μ))-模糊正关联理想。
6 (∈,∈∨q(λ,μ))-模糊正关联理想的链条件
下面给出KU代数正关联理想的链条件的新概念,并利用(∈,∈∨q(λ,μ))-模糊正关联理想的性质对链条件进行刻画。
定义13(链条件)设Ai(i=1,2,…)是KU代数G的正关联理想,如果它的任意正关联理想降链序列A1⊃A2⊃…An⊃…只有有穷项,即对于任意含无穷项的正关联理想降链序列A1⊇A2⊇…An⊇…必定有一个正整数存在,自m项后的所有正关联理想都相等,即Am=Am+1=…,则称G关于正关联理想满足降链条件(也称G关于正关联理想是阿丁的)。
类似地,可以定义G关于正关联理想的升链条件(也称G关于正关联理想是诺特的)。
定义14(对偶良序集)设集合(S,≤)为一偏序集,≤是其偏序关系,若对任意的S的非空子集,在其序下都有最大元素,则称≤为对偶良序关系,(S,≤)为对偶良序集。
定理19设G是KU代数,{Ai}i∈I是G的正关联理想族,若∀i,j∈I有Ai⊆Aj或Aj⊆Ai,那么A=Ai是G的正关联理想。
证明因为Ai(i=1,2,…)是G的正关联理想,所以0∈Ai,即0∈Ai=A。又因为∀x,y,z∈G,若z∗(x∗y)∈A且z∗x∈A,所以存在i1、i2使得z∗(x∗y)∈Ai1,z∗x∈Ai2。由已知Ai1⊆Ai2或Ai2⊆Ai1,不妨设Ai1⊆Ai2,从而z∗(x∗y)∈Ai1⊆Ai2。又因为Ai2是正关联理想,故z∗y∈Ai2⊆Ai1。所以A=Ai是G的正关联理想。
定理20设G为KU代数,{Ai}i∈I是G的正关联理想族,那么A=Ai是G的正关联理想。
证明∀i∈I,因为Ai是G的正关联理想,所以0∈Ai,即0∈Ai=A。又∀x,y,z∈G,若z∗(x∗y)∈A且z∗x∈A,于是∀i∈I,有z∗(x∗y)∈Ai及z∗x∈Ai。因为Ai是G的正关联理想,故z∗y∈Ai,所以z∗y∈A。因此,A=Ai是G的正关联理想。
定理21设G关于正关联理想满足降链条件,A是G的任意的(∈,∈∨q(λ,μ))-模糊正关联理想,则在Im(A)⋂[λ,μ]上不存在无穷上升序列。
证明(反证法)假设{ti|i=0,1,2,…}是Im(A)⋂[λ,μ]上的无穷上升序列,则t0<t1<…<μ,因此t1<t2<…<μ也是一个无穷严格升链,且ti∈(λ,μ],i=1,2,…,并且∃xi∈G使得A(xi)=ti。由定理3知道Ati是G的正关联理想,又因为A(xi-1)=ti-1<ti,所以xi-1∉Ati。因此Ati⊂Ati-1,于是At1⊃At2⊃…是关于正关联理想的无穷降链,这与G关于正关联理想满足降链条件矛盾。
定理22设G是KU代数,则G关于正关联理想是诺特的充要条件是对G的任意(∈,∈∨q(λ,μ))-模糊正关联理想A,Im(A)⋂[λ,μ]是良序集。
证明必要性:设A是G的(∈,∈∨q(λ,μ))-模糊正关联理想。由定理3可知,A是G的广义模糊正关联理想。假设Im(A)⋂[λ,μ]不是良序集,则在Im(A)⋂[λ,μ]存在严格递减序列{ti},且ti≠λ(否则就没有无穷降链),i=1,2,…,且∃xi∈G使得A(xi)=ti,因此At1⊆⊆⊆…。又由于ti∈(λ,μ],由定理3可知Ati是正关联理想。若>,则A()=<。因此∉,故⊂。从而⊂⊂⊂…是G的关于正关联理想的严格升链,这与G是诺特的矛盾。
充分性:若对G的任意广义模糊正关联理想A,Im(A)⋂[λ,μ]是良序集,但G不是诺特的,则存在严格升链A1⊂A2⊂A3⊂…,其中Ai是G的正关联理想。由定理19可知,Ai是G的正关联理想。定义模糊子集:
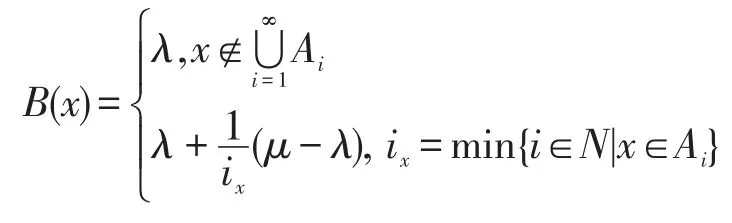
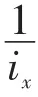
下面证明B是G的广义模糊正关联理想。
因为Ai是正关联理想,故0∈Ai(i=1,2,…),i0=1。所以∀x∈G,B(0)∨λ=(λ+(μ-λ))∨λ=μ≥B(x)∧μ。
∀x,y,z∈G,下面分4种情况进行讨论:
①如果iz∗(x∗y)=iz∗x,设m=iz∗(x∗y)。因为z∗(x∗y)∈Am,z∗x∈Am,而Am是G的正关联理想,所以z∗y∈Am。又由B的定义知i≤m,故B(z∗y)∨λ=(λ+
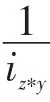
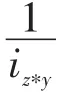
③若iz∗(x∗y)<iz∗x,则同理可证B(z∗y)∨λ≥B(z∗(x∗y))∧B(z∗x)∧μ。
综上所述,B是G的(∈,∈∨q(λ,μ))-模糊正关联理想,矛盾,因此G关于正关联理想是诺特的。
推论6若G的每个(∈,∈∨q(λ,μ))-模糊正关联理想的值域是有限集,则G关于正关联理想是诺特的。
证明因为Im(B)⋂[λ,μ]=Im(B)是有限集,所以它是良序集,由定理22知G是诺特的。
定理23若G的每个(∈,∈∨q(λ,μ))-模糊正关联理想的值域是有限集,则G关于正关联理想是阿丁的。
证明假设G关于正关联理想不是阿丁的,则存在G的正关联理想的无穷严格降链A1⊃A2⊃···。若A1≠G,那么取A0=G,得严格降链G=A0⊃A1⊃A2⊃···。总可以得到G的正关联理想的严格降链G=A0⊃A1⊃A2⊃···。
定义G的模糊子集B:
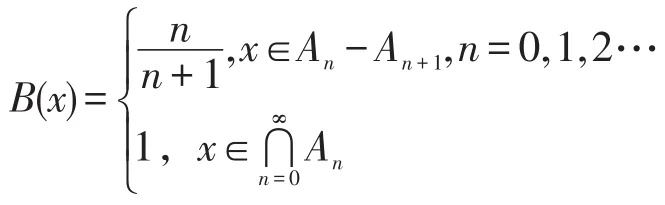
∀x,y,z∈G,以下分4种情况讨论:
因此,B是G的广义模糊正关联理想。由定理3可知,B也是G的(∈,∈∨q(λ,μ))-模糊正关联理想。然而B的值域具有无限不同值,故与题设矛盾。
推论7若G的每个(∈,∈∨q(λ,μ))-模糊正关联理想的值域是有限集,则G关于正关联理想是阿丁的且是诺特的。
证明因为G的每个(∈,∈∨q(λ,μ))-模糊正关联理想的值域是有限集,所以由定理23知G是阿丁的。又由推论6知G是诺特的。
定理24设G是KU代数,则G关于正关联理想是阿丁的充要条件是对G的任意(∈,∈∨q(λ,μ))-模糊正关联理想A,Im(A)⋂[λ,μ]是对偶良序集。
证明必要性:设A是G的(∈,∈∨q(λ,μ))-模糊正关联理想。由定理3可知,A是G的广义模糊正关联理想。假设Im(A)⋂[λ,μ] 不 是 对 偶 良 序 集,则 在Im(A)⋂[λ,μ]中存在严格递增序列{ti}(i=0,1,2,…),故ti>t0≥λ(i=1,2,…)且 {ti}(i=1,2,…)也是严格递增序列,因此ti∈(λ,μ](i=1,2,…)且At1⊇At2⊇At3⊇…。
由定理3可知,Ati(i=1,2,…)是正关联理想。又因为ti∈Im(A),所以∃xi∈G使得A(xi)=ti。若i<j,则A(xi)=ti<tj。因此xi∉Atj,故Ati⊃Atj。从而At1⊃At2⊃At3⊃…是G的关于正关联理想的严格降链,这与G是阿丁的矛盾。
充分性:若对G的任意广义模糊正关联理想A,Im(A)⋂[λ,μ]是对偶良序集,但G不是阿丁的,则存在严格降链A1⊃A2⊃A3⊃…,其中Ai是G的正关联理想。由定理19可知,Ai是G的正关联理想。
定义模糊子集:
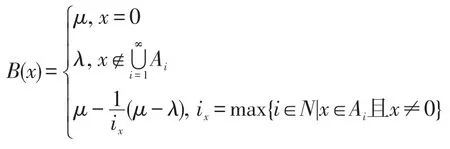
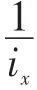
下面证明B是G的广义模糊正关联理想。因为Ai是正关联理想,故0∈Ai(i=1,2,3…),所以∀x∈G,B(0)∨λ=μ≥B(x)∧μ。∀x,y,z∈G,分两种情况进行讨论:
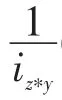
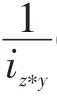
③若iz∗(x∗y)<iz∗x,则同理可证B(z∗y)∨λ≥B(z∗(x∗y))∧B(z∗x)∧μ。
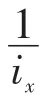
7 结束语
本文给出了 KU 代数的(∈,∈∨q(λ,μ))-模糊正关联理想的概念,用点态化的方法讨论了它的等价刻画及其他一系列基本性质,并指出它有丰富的层次结构。而点态化的方法更接近经典数学的方法,这是本文的一个特色。用 KU 代数的(∈,∈∨q(λ,μ))-模糊正关联理想刻画KU代数的正关联理想的链条件,比用通常KU代数的模糊正关联理想对它进行刻画有更弱的条件,这为用模糊数学的方法对经典代数进行研究提供了一种新的思路。此外,还给出了寻找KU代数的正关联理想的算法(见附录),并通过计算机编程找出正关联理想,这有助于给出例子以说明KU代数的(∈,∈∨q(λ,μ))-模糊正关联理想是一种新型模糊代数结构。
这些工作丰富了模糊集理论的研究,促进了KU代数理论研究的深入发展。进一步的工作是引入KU 代数的其他类型的(∈,∈∨q(λ,μ))-模糊理想并对其进行刻画,还可以对KU代数与FI代数及格蕴涵代数的关系进行研究。
[1]Zadeh LA.Fuzzy sets[J].Information and Control,1965,8(3):338-353.
[2]RosenfeldA.Fuzzy groups[J].Journal of MathematicalAnalysis andApplications,1971,35(3):512-517.
[3]Kuroki N.On fuzzy ideals and fuzzy bi-ideals in semigroups[J].Fuzzy Sets and Systems,1981,5(2):203-215.
[4]Kuroki N.Fuzzy semiprime ideals in semigroups[J].Fuzzy Sets and Systems,1982,8(1):71-79.
[5]Kuroki N.On fuzzy semigroups[J].Information Sciences,1991,53(3):203-236.
[6]Kuroki N.Fuzzy generalized bi-ideals insemigroups[J].Information Sciences,1992,66(3):235-243.
[7]Kuroki N.Fuzzy semiprime quasi-ideals in semigroups[J].Information Sciences,1993,75(3):201-211.
[8]Swamy U M,Swamy K L N.Fuzzy prime ideals of rings[J].Journal of Mathematical Analysis and Applications,1988,134(1):94-103.
[9]Pu Paoming,Liu Yingming.Fuzzy topology I neighborhood structure of a fuzzy point and Moore-Smith convergence[J].Journal of Mathematical Analysis and Applications,1980,76(2):571-599.
[10]Pu Paoming,Liu Yingming.Fuzzy topology II product and quotient spaces[J].Journal of Mathematical Analysis and Applications,1980,77(1):20-37.
[11]Bhakat S K,Das P.On the definition of a fuzzy subgroup[J].Fuzzy Sets Systems,1992,51(2):235-241.
[12]Bhakat S K,Das P.(∈,∈∨q)-fuzzy subgroup[J].Fuzzy Sets and Systems,1996,80(3):359-368.
[13]Jun YB,Kang M S.Fuzzy positive implicative ideals of BCK-algebras based on the theory of falling shadows[J].Computers and Mathematics with Applications,2011,61(1):62-67.
[14]Tebu S F,Lele C,Nganou JB.Fuzzy n-fold BCI-positive implicative ideals in BCI-algebras[J].International Journal of Mathematics and Mathematical Sciences,2012,4:628931.
[15]Zulfiqar M.Some properties of(α,β)-fuzzy positive implicative ideals in BCK-algebras[J].Acta Scientiarum Technology,2013,35(2):371-377.
[16]Liao Zuhua,Gu Hui.(∈,∈∨q(λ,μ))-fuzzy normal subgroup[J].Fuzzy Systems and Mathematics,2006,20(5):47-53.
[17]Zhang Jianzhong,Fu Xiaobo,Liao Zuhua.(∈,∈∨q(λ,μ))-fuzzy ideal of N(2,2,0)algebra[J].Journal of Frontiers of Computer Science&Technology,2013,7(11):1048-1056.
[18]Zhu Chan,Liao Zuhua,Luo Xiaotang,et al.(∈,∈∨q(λ,μ))-fuzzy complemented semirings[J].Fuzzy Systems and Mathematics,2013,27(5):47-54.
[19]Zhang Jianzhong,Fu Xiaobo,Liao Zuhua.(∈,∈∨q(λ,μ))-fuzzy positive implicative ideal of N(2,2,0)algebra[J].Journal of Frontiers of Computer Science and Technology,2014,8(5):622-629.
[20]Fan Xiaowei,Liao Zuhua,Fan Yingying,et al.(∈,∈∨q(λ,μ))-fuzzyΓ-completely prime ideals ofΓ-semigroups[J].Fuzzy Systems and Mathematics,2014,28(2):52-61.
[21]Fu Xiaobo,Liao Zuhua,Zheng Gaoping,et al.(∈,∈∨q(λ,μ))-fuzzy LI-ideals of lattice implication algebra[J].Fuzzy Systems and Mathematics,2014,28(5):41-50.
[22]Zhang Jianzhong,Fu Xiaobo,Liao Zuhua.(∈,∈∨q(λ,μ))-fuzzy associative ideal of N(2,2,0)algebra[J].Computer Engineering andApplications,2014,50(12):54-58.
[23]Fu Xiaobo,Zhan Xueqiu,Liao Zuhua.(∈,∈∨q(λ,μ))-fuzzy filter of lattice implication algebra[J].Journal of Frontiers of Computer Science and Technology,2014,8(3):376-384.
[24]Fu Xiaobo,Liao Zuhua.(∈,∈∨q(λ,μ))-fuzzy prime filter of lattice implication algebra[J].Journal of Frontiers of Computer Science and Technology,2015,9(2):227-233.
[25]Lu Teng,Liao Zuhua,Liao Cuicui,et al.-fuzzy ideals of incline algebra[J].Journal of Frontiers of Computer Science and Technology,2016,10(8):1191-1200.
[26]Prabpayak C,Leerawat U.On ideas and congruences in KU-algebras[J].Scientia Magna,2009,5(1):54-57.
[27]Prabpayak C,Leerawat U.On isomorphisms of KU-algebras[J].Scientia Magna,2009,5(3):25-31.
[28]RezaeiA,Saeid AB,Borzooei RA.KU-algebras are equivalent to commutative self-distributive BE-algebra[J].Bollettino di Matematica Pura edApplicata,2014,7:1-8.
[29]Wu Wangming.Fuzzy implication algebras[J].Fuzzy Systems and Mathematics,1990,4(1):56-64.
[30]Xu Yang,Ruan Da,Qin Keyun,et al.Lattice-valued logic[M].Berlin,Heidelberg:Springer,2003.
[31]Mostafa S M,Abd-Elnaby MA,Yousef M M M.Fuzzy ideals of KU-algebras[J].International Mathematical Forum,2011,6(63):3139-3149.
[32]Mostafa S M,Abd-Elnaby MA,Elgendy OR.Intuitionistic KU-ideals in fuzzy KU-algebras[J].International Journal of Mathematical Sciences and Applications,2011,1(3):1379-1384.
[33]Mostafa S M,Kareem F F.N-fold commutative KU-algebras[J].International Journal ofAlgebra,2014,8(6):267-275.
[34]Gulistan M,Shahzad M,Ahmed S.On(α,β)-fuzzy KU-ideals of KU-algebras[J].Afrika Matematika,2015,26(3):651-661.
[35]Gulistan M,Shahzad M,Yaqoob N.On(∈,∈∨qk)-fuzzy KU-ideals of KU-algebras[J].Acta Universitatis Apulensis,2014,39:75-83.
[36]Muhiuddin G.Bipolar fuzzy KU-subalgebras/ideals of KU-algebras[J].Annals of Fuzzy Mathematics and Informatics,2014,8(3):409-418.
[37]Senapati T,Shum K P.Atanassov's intuitionistic fuzzy binormed KU-ideals of a KU-algebra[J].Journal of Intelligent&Fuzzy Systems,2016,30(2):1169-1180.
[38]Noether E.Idealtheorie in Ringbereichen[J].Mathematische Annalen,1921,83(1):24-66.
[39]Artin E.Zur Theorie der hyperkomplexen Zahlen[J].Abhandlungen Aus Dem Mathematischen Seminar der Universität Hamburg,1927,5(1):251-260.
[40]Meng Daoji,Wang Liyun,Yuan Lamei.Abstract algebraⅢ—commutative algebra[M].Beijing:Science Press,2016.
[41]Mordeson J N,Malik D S.Fuzzy commutative algebra[M].Singapore:World Scientific Publishing,1998.
[42]Hu Baoqing.Foundations of fuzzy theory[M].2nd ed.Wuhan:Wuhan University Press,2010.
附中文参考文献:
[17]张建忠,傅小波,廖祖华.N(2,2,0)代数的(∈,∈∨q(λ,μ))-模糊理想[J].计算机科学与探索,2013,7(11):1048-1056.
[18]朱婵,廖祖华,罗晓棠,等.(∈,∈∨q(λ,μ))-模糊可补半环[J].模糊系统与数学,2013,27(5):47-54.
[19]张建忠,傅小波,廖祖华.N(2,2,0)代数的(∈,∈∨q(λ,μ))-模糊正关联理想[J].计算机科学与探索,2014,8(5):622-629.
[20]范晓威,廖祖华,范莹莹,等.Γ-半群的(∈,∈∨q(λ,μ))模糊Γ-完全素理想[J].模糊系统与数学,2014,28(2):52-61.
[21]傅小波,廖祖华,郑高平,等.格蕴涵代数的(∈,∈∨q(λ,μ))-模糊LI理想[J].模糊系统与数学,2014,28(5):41-50.
[22]张建忠,傅小波,廖祖华.N(2,2,0)代数的(∈,∈∨q(λ,μ))-模糊结合理想[J].计算机工程与应用,2014,50(12):54-58.
[23]傅小波,战学秋,廖祖华.格蕴涵代数的(∈,∈∨q(λ,μ))-模糊滤子[J].计算机科学与探索,2014,8(3):376-384.
[24]傅小波,廖祖华.格蕴涵代数的(∈,∈∨q(λ,μ))-模糊素滤子[J].计算机科学与探索,2015,9(2):227-233.
[25]路腾,廖祖华,廖翠萃,等.坡代数的(-∈,-∈∨(λ,μ))-模糊理想[J].计算机科学与探索,2016,10(8):1191-1200.
[29]吴望名.Fuzzy蕴涵代数[J].模糊系统与数学,1990,4(1):56-64.
[40]孟道骥,王立云,袁腊梅.抽象代数Ⅲ——交换代数[M].北京:科学出版社,2016.
[42]胡宝清.模糊理论基础[M].2版.武汉:武汉大学出版社,2010.
附录:
查找KU代数正关联理想的程序
#include〈iostream〉
using namespace std;
int KU(int a,int b);//KU代数计算函数
voidideals2(intx);//查找KU代数有两个元素的正关联理想
void ideals3(intx,inty);//查找KU代数有三个元素的正关联理想
void ideals4(intx,inty,intz);//查找KU代数有四个元素的正关联理想
On(∈,∈∨q(λ,μ))-Fuzzy Positive Implicative Ideals of KU-Algebras*
LI Lun1,2,LIAO Zuhua1,2,3+,CHEN Liuhong1,2,SONG Wei4,WU Shuzhong1,ZHU Xiaoying1
1.School of Science,Jiangnan University,Wuxi,Jiangsu 214122,China
2.Honors School,Jiangnan University,Wuxi,Jiangsu 214122,China
3.Institute of Intelligence System&Network Computing,Jiangnan University,Wuxi,Jiangsu 214122,China
4.School of Internet of Things Engineering,Jiangnan University,Wuxi,Jiangsu 214122,China
+Corresponding author:E-mail:liaozuhua57@163.com
LI Lun,LIAO Zuhua,CHEN Liuhong,et al.On(∈,∈∨q(λ,μ))-fuzzy positive implicative ideals of KU-algebras.Journal of Frontiers of Computer Science and Technology,2017,11(8):1324-1339.
Firstly,this paper gives the concepts of pointwise(∈,∈∨q(λ,μ))-fuzzy positive implicative ideals and generalized fuzzy positive implicative ideals of KU-algebras,obtains some equivalent characterizations of(∈,∈∨q(λ,μ))-fuzzy positive implicative ideals of KU-algebras,and points the richer hierarchical structure of the fuzzy positive implicative ideals.Secondly,this paper acquires the properties that intersections,unions,homomorphic image and homomorphic preimage(under certain condition)of(∈,∈∨q(λ,μ))-fuzzy positive implicative ideals of KU-algebras are also(∈,∈∨q(λ,μ))-fuzzy positive implicative ideals.Then,this paper investigates the direct product and proje-ction of(∈,∈∨q(λ,μ))-fuzzy positive implicative ideals of KU-algebras.At last,this paper introduces the new concepts of the descending(ascending)chain conditions of the positive implicative ideals of KU-algebras,which are studied by using the properties of(∈,∈∨q(λ,μ))-fuzzy positive implicative ideals.
KU-algebras;(∈,∈∨q(λ,μ))-fuzzy positive implicative ideals;homomorphic mapping;projection;descending(ascending)chain condition
was born in 1981.He
the Ph.D.degree from Chonbuk National University in 2009.Now he is an associate professor and M.S.supervisor at Jiangnan University,and the member of IEEE and CCF.His research interests include pattern recognition,artificial intelligence,data mining,information retrieval and knowledge discovery,etc. 宋威(1981—),男,湖北恩施人,2009年于韩国全北国立大学获得博士学位,现为江南大学副教授、硕士生导师,IEEE、CCF会员,主要研究领域包括模式识别,人工智能,数据挖掘,信息检索,知识发现等。




LI Lun was born in 1995.He is a student at School of Science,Jiangnan University,and the member of CCF.His research interests include computer science,fuzzy and rough algebra,etc.李论(1995—),男,河南郑州人,江南大学理学院粒计算研究所学生,CCF学生会员,主要研究领域为计算机科学,模糊与粗糙代数等。

LIAO Zuhua was born in 1957.He is a professor and M.S.supervisor at Jiangnan University,and the member of CCF.His research interests include artificial intelligence and granular computing,etc.廖祖华(1957—),男,江西奉新人,江南大学教授、硕士生导师,CCF会员,主要研究领域为人工智能,粒计算等。发表学术论文100多篇。

CHEN Liuhong was born in 1995.She is a student at School of Science,Jiangnan University.Her research interests include computer science,fuzzy and rough algebra,etc.陈柳红(1995—),女,重庆涪陵人,江南大学理学院粒计算研究所学生,主要研究领域为计算机科学,模糊与粗糙代数等。

WU Shuzhong was born in 1961.He is an associate professor at Jiangnan University.His research interest is combinatorial mathematics.吴树忠(1961—),男,江苏丹阳人,江南大学副教授,主要研究领域为组合数学。

ZHU Xiaoying was born in 1964.She is an associate professor at Jiangnan University.Her research interest is fuzzy algebra.朱晓英(1964—),女,江苏无锡人,江南大学副教授,主要研究领域为模糊代数。
A
:O159
*The National Natural Science Foundation of China under Grant Nos.61170121,11401259,61673193(国家自然科学基金);the Natural Science Foundation of Jiangsu Province under Grant No.BK20151117(江苏省自然科学基金);the Undergraduate Innovation and Entrepreneurship Training Program of China under Grant No.201610295005(国家大学生创新训练项目).
Received 2017-03,Accepted 2017-05.
CNKI网络优先出版:2017-05-23,http://kns.cnki.net/kcms/detail/11.5602.TP.20170523.1250.004.html
ISSN 1673-9418 CODEN JKYTA8
Journal of Frontiers of Computer Science and Technology 1673-9418/2017/11(08)-1324-16
10.3778/j.issn.1673-9418.1703085
E-mail:fcst@vip.163.com
http://www.ceaj.org
Tel:+86-10-89056056
