双向消元法在解法方程的应用
2017-08-16万应玲甘肃建筑职业技术学院甘肃兰州730050
万应玲(甘肃建筑职业技术学院,甘肃 兰州 730050)
双向消元法在解法方程的应用
万应玲(甘肃建筑职业技术学院,甘肃 兰州 730050)
测量平差中的条件平差法和间接平差法需要解算法方程。法方程是一些多元一次方程构成的方程组,教学过程中学生手算求解过程一般采用高斯约化法,由于缺乏对结果的校核而容易出现计算错误。本文作者结合自己的教学经验,通过具体实例介绍了双向消元的解析过程,优化了其计算方法并经过步步校核消元确保了结果的正确性。
高斯约化法;双向消元法;检核计算
在测量平差中, 各种观测量与已知条件以及各种图形几何条件之间可组成条件方程组或观测量的误差方程组。进行平差解算时,首先对方程组线性化, 形成满足最小二乘(或满足最小范数)条件的线性化平差函数模型[1]。平差问题的求解最后都归结为线性方程组的求解过程。因而, 解算线性方程组是解算平差问题的关键[2]。在传统的解算过程中是将各种平差方程组形成法方程, 通过高斯约化来进行求解[3]。高斯约化法是按照方程的顺序,从上向下逐个消元,最后使方程组变为一个三角形方程组[4]。高斯约化法对消元过程提出了具体规定和要求,编制了一定的格式,具有较强的规律性。但高斯约化法原理的推导符号多,过程繁[5]。有些数据的得出需多个数据参与计算,若有差错,难以快速找到原因[6]。本文采用双向消元法,最后将每个方程简化为一元一次方程并经过步步校核消元确保了结果的准确性。
1 计算实例
设某法方程中有r个多元一次方程,采用双向消元法解算过程如下:1)将第一个方程的第一个未知数系数变为1,用其消去其它方程的第一个未知数;2)在第一步所得的方程组中,将第二个方程的第二个未知数系数变为1(第一个未知数已消去),用其向上、向下消去各方程的第二个未知数。3)这样依次处理,到第r步时,第r个方程就变为一元一次方程,各方程未知数的序号与该方程序号相同,且系数为1,这样各未知数的解随之可得。为了进一步明确双向消元法的具体解算过程,可以通过下列表中的数据实例进行计算。
表1列出了某一条件平差计算过程的法方程系数。为了叙述简便,将表1、表2中的某几个方程编上带圆圈的序号。将表1中方程(1)的各系数(包括∑,∑表示该行左边各数之和)除以K1的系数2.7552,得表2中的方程(1)。在表2方程(1)中,S是由表1中方程(1)的∑除以2.7552而来,其∑仍为左边各数之和,当∑和S相等时,说明方程(1)从表1到表2的推算没有错误。
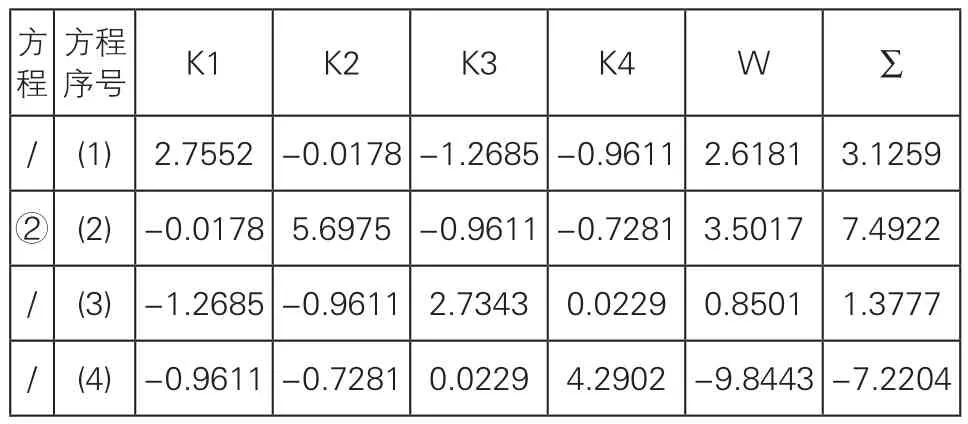
表1 法方程系数表
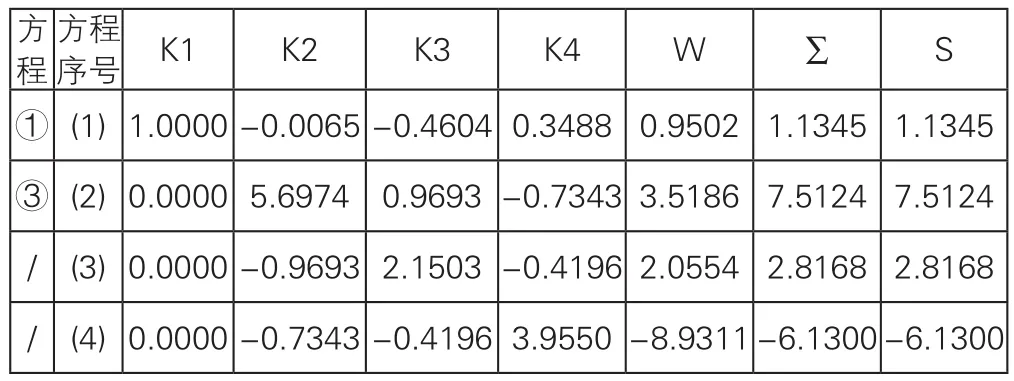
表2 法方程系数推算表
将方程①乘以方程②K1系数的相反数0.0178并与方程②相加,则消去了方程②的未知数K1得方程③,该过程是逐项进行的,即:

将∑的结果填到方程③的5栏中,它是推算的方程③中各项系数应有的和。然后再对方程③各项系数实际相加,其和也是7.5124。这说明由方程①、②推算方程③是正确的。
从方程①、②、③来看,其中∑是本方程内左边各系数之和,称为实际和。方程①、③是由相关方程推算来的,其中S是由这些相关方程中的∑推算的,称为推算和。若个别相关方程中的∑和S不一致时,仍要用∑推算S,这样可以减少误差的积累。当∑和S相等或末位数相差不超过3时,说明推算过程正确,若∑和S相差较多,说明推算过程有误,这时应先检查S是否正确,当S无误时,再对各系数的计算进行检查。
用同样方法消去表1中方程(3)、(4)的未知数K1,得表2中的方程(3)、(4)。表2中的方程(1)是用来消去其它方程未知数K1的,是消元的基础,把它称为“基方程”。为了计算中减少差错,将基方程的系数下画一横线以与其它方程相区别,而S下不需要画线。因S是消元中计算的结果,没有参与任何计算,其作用就是与∑相互校核,检查消元过程中有无错误。消去K1后,将表2中方程(2)的K1系数变为1,用其向上、向下消去该表中其它方程中的K2,得到表3的结果。
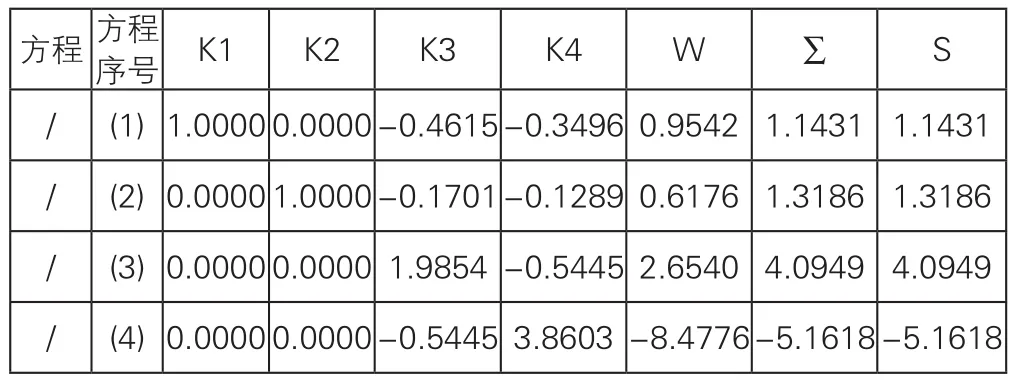
表3 法方程系数推算表
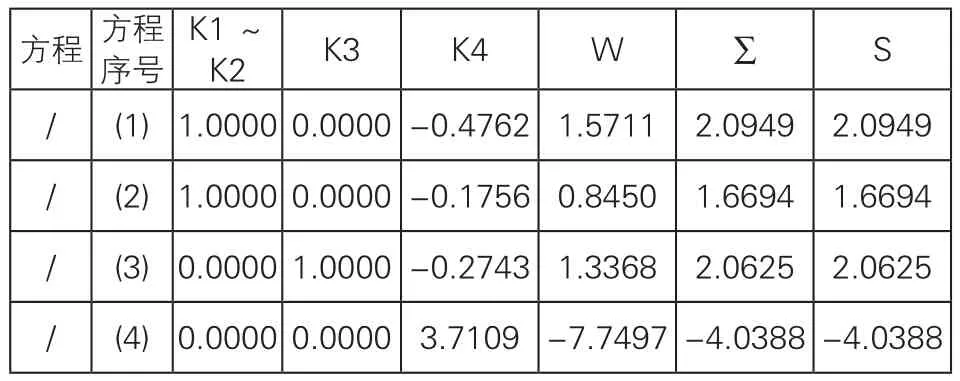
表4 法方程系数推算表
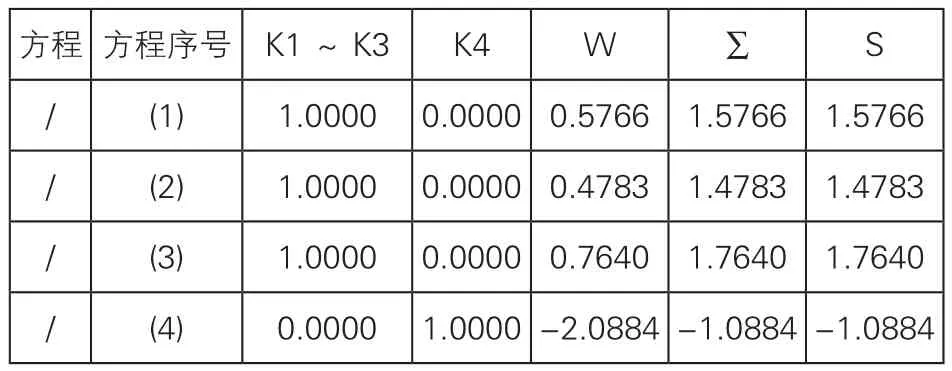
表5 法方程系数推算表
用同样的方法消去K3、K4,其结果如表4和表5所示。为使计算表格简洁,可将消去未知数的栏进行合并。如表4的K1~K2栏,表5的K1~K3栏。该栏内的数字1,表示的只是和相应方程同序号的未知数系数为1,其余未知数系数为0;而该栏内的0,表示合写的未知数都已消去,系数都为0。
由表5可直接得出未知数K的值。

2 分析讨论
若采用高斯约化法利用消元回带过程求解方程,如果中途有一个未知数求解有误,则后面所有未知数的解都是错的,且很难快速找到错误的原因。高斯约化法充分利用了方程的对称性, 对于解非线性对称方程组问题很难实现[7],而在双向消元法中只有向下消元时才利用对称性。若有时计算的值并不完全对称,这时以计算值为准,保留其“不对称性”,以保证该方程的∑和S不会相差太多。
3 结 语
高斯约化法和双向消元法的基本思想都通过将一个方程乘以或除以某个常数,以及将两个方程相加减这两种手续,逐步减少方程中的变元的数目,最终使每个方程仅含一个变元,从而得出所求的解。高斯约化法的求解过程分为消元过程和回代过程两个环节。这种方法缺点是一旦计算过程出现错误从而导致整个计算错误,且很难发现错误的原因。而采用双向消元法可同时求出法方程中各个未知数的解,不需要回代,并且这些一元一次方程都是经过一步步校核消元而得出的,因此这些未知数的解都是正确可靠的。
[1]陶本藻.非线性与线性平差偏差的分布特征[J].测绘工程,1998(4):7-12.
[2]张东明,吕翠华,李明.点松弛法在测量平差方程组解算中的应用[J].科学技术与工程,2010,10(24):5981-5984.
[3]张东明,李明,肖建虹.利用迭代方法求解测量平差中的线性方程组[J].地矿测绘,2003,19(4):15-17.
[4]赵艳宇 .Gauss消去法[J].电大理工,2013(2):51-52.
[5]刘成军.基于消息传递接口的线性方程组并行计算研究—以改进的高斯消元法为例[J].软件,2013,34(1):119-120.
[6]颜平.测量平差[M].北京:中国建筑工业出版社,2002:42~ 45.
[7]袁功林,李向荣.解非线性对称方程组问题的具有下降方向的近似高斯-牛顿基础的BFGS方法[J].运筹学学报,2004,8(4):10-26.
Two-way elimination method applied in solution normal equation
Conditional adjustment method and adjustment of observation equations needs solution normal equation.The normal equation is an equation of some multivariate equations.In the process of teaching,the calculation process of the students is generally adopted by Gaussian elimination,Due to the lack of verification of the results and prone to error.In this paper, the author combined with his own teaching experience,Through concrete examples this paper introduces the analytical process of two-way elimination method.Its calculation method was optimized,And after the check elimination step by step to ensure the validity of the results.
Gaussian elimination;two-way elimination method;check calculation
TB302文献辨识码:B
1003-8965(2017)01-0050-02
