高黏流体竖直管外降膜流动的三维数值模拟

王 飞，陈世昌，马建平，张先明，陈文兴

(浙江理工大学纺织纤维材料与加工技术国家地方联合工程实验室，杭州 310018)



高黏流体竖直管外降膜流动的三维数值模拟

王 飞，陈世昌，马建平，张先明，陈文兴

(浙江理工大学纺织纤维材料与加工技术国家地方联合工程实验室，杭州 310018)

基于计算流体力学(CFD)技术,采用流体体积法(VOF)追踪气液两相界面的位置变化，对高黏流体竖直管外竖直降膜流动进行了三维数值模拟研究，考察了高黏流体在光滑直管和波形管管外降膜的自由面变化、膜厚和速度分布等流体动力学行为。结果表明：高黏流体在直管和波管管外做降膜流动的成膜厚度均随黏度的增大而增大，膜面速度则有所减小，相同黏度的流体其膜厚和膜面速度均随流量的增加而显著增大。高黏流体在光滑直管外降膜流动一段距离后，其膜面速度和膜厚趋于稳定，而对于波形管外的降膜流动，其膜面速度和液膜厚度均随波节做周期性变化，且在波峰附近时液膜最薄，但膜面速度最大，在波谷附近液膜最厚，但膜面速度最小。

降膜流动；数值模拟；高黏流体；膜厚；速度分布

0 引 言

降液膜流动是液体在重力作用下沿壁面呈膜状运动，属于典型的受迫运动，液膜一侧与壁面接触，另一侧暴露在气体中形成自由界面，因其具有小流量、小温差、高热质传递系数、结构简单且动力消耗小等独特优点已在工程热物理、机械加工、石油化工等重要工业领域广泛应用。

Nusselt[1]首次提出了描述降液膜的理论，以层流、无波动的假设为基础，得到了降膜过程中的膜厚和速度分布等参数，该理论如今已成为研究降膜流动的经典理论。Moran等[2]研究了溴化锂溶液在倾斜板上低雷诺数下降膜过程中液膜厚度与膜面速度分布情况。Gao等[3]和马学虎等[4]运用数值模拟方法，选取流体体积法(VOF)模型研究了溴化锂溶液在不同边界条件下自由界面沿平板表面的变化过程。Liu等[5]采用VOF法，模拟了水与空气在竖直管内做两相顺流降膜流动，研究了液膜形态的变化规律。Garcia等[6]以水为工质通过实验研究发现波节管的热质传递性能优于直管。

目前关于降液膜流动的研究均以水、溴化锂溶液、甘油等低黏流体为工质在平板上或管道内的流动展开，而关于高黏流体在竖直管外降膜流动的相关研究还很少。本文以直管和波管为降膜支撑件，针对高黏流体在竖直管外降膜流动利用计算机流体力学(CFD)软件Fluent进行模拟计算，探索膜厚与速度分布规律及其影响因素，以期为进一步研究管外膜状流动中的热质传递机理提供基础。

1 模型与方法

1.1 物理模型

通过Pro/E软件对竖直管外降膜流动进行三维建模，并选用三维稳态Navie-Stokes方程描述降膜流场。图1为计算域的物理模型，其中直管半径为16 mm，波节管的波峰和波谷半径分别为20 mm和16 mm，降膜高度均为500 mm。

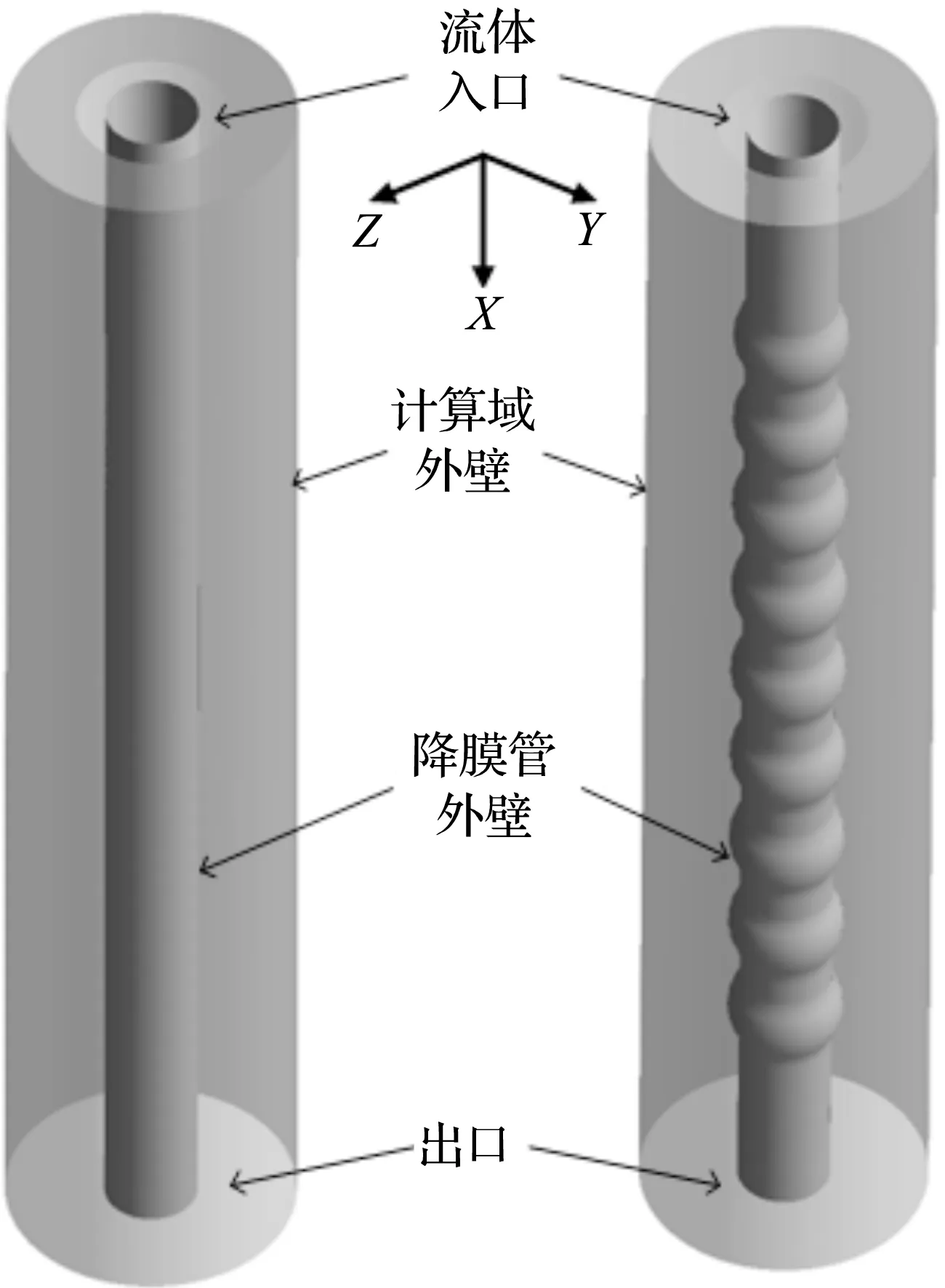
图1 计算域物理模型示意图

气液两相降膜流动属于多相流模型，可选用VOF法捕捉自由界面，这种方法在解决复杂的自由表面流动问题具有很大优势，特别适合计算气液两相流。

1.2 流体物性

模拟流体为聚二甲基硅氧烷，其抗剪切能力强，且在低温和高温下稳定性突出，其物理性质见表1。

表1 硅油流体的物理性质

1.3 控制方程

本文在等温层流三维流动数值模拟中，根据高黏流体流动特点做出如下假设与简化：a)由于高黏降膜过程剪切速率较小，假设料液处在牛顿平台区，且为稳态流动；b)液膜在降膜管外壁的流动是层流；c)液体物性为常数且壁面无滑移。

连续性方程可用式(1)表示：

(1)

动量方程可用式(2)-式(4)表示：

(2)

(3)

(4)

其中：u、v和w分别为液膜表面流体在X、Y和Z三个方向的速度，m/s，F表示表面张力源项，可表示为：

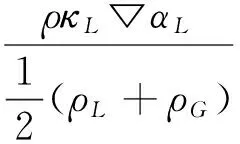
(5)

其中：σLG表示气液界面的表面张力系数, N/m；κL表示界面曲率，αL表示液体的体积分数

VOF法通过计算单元格内第q相的体积分率αq的大小而确定自由界面的位置。在单元格内，若αq=1则表明该单元内充满第q相，αq=0则表明该单元内没有第q相；当0<αq<1则表明该单元内既有第q相又有其他相，即该单元内存在自由界面。自由界面分布可由式(6)计算得到。

(6)

控制方程中的物性参数如密度、黏度等通过以下各组分的加权计算：

ρ=αLρL+(1-αL)ρG

(7)

μ=αLμL+(1-αL)μG

(8)

其中：ρ、μ分别为气液混合相的密度和动力黏度，kg/m3、Pa·s；ρL、μL分别为流体的密度和动力黏度，kg/m3、Pa·s；ρG、μG分别为空气的密度和动力黏度，kg/m3、Pa·s。

1.4 边界条件和求解方法

计算前计算域内没有液体只有空气，故采用VOF法进行模拟计算时只有液体入口没有空气入口，且入口采用速度入口，出口选择压力出口，采用三维双精度进行计算，选取PISO算法进行压力-速度耦合，使用二阶迎风格式求解离散方程。通过给定不同的入口速度来限定流量，整个模拟过程均在常温常压下进行。由于液体不可压缩，则由连续性方程可得出降膜时液体的质量流量φ和入口初速度v0以及流体密度ρ之间的关系式如下。

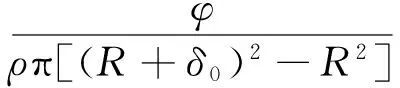
(9)

其中：R为降膜管半径，m；δ0为初始膜厚，m。

根据以上假设与边界条件的设定，降液膜膜厚的理论公式如下。

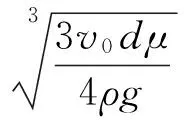
(10)

其中：v0是入口初速度，m/s；d为当量直径，m。

2 网格划分与验证

2.1 网格划分与无关性验证

对光滑直管以及波管管外流场区域运用ICEM软件进行三维网格的划分，六面体网格在计算精度、变形特性、划分网格数量、抗畸变程度及再划分次数等方面具有明显优势[7]。考虑到表面张力对液膜流动的影响，本文采用精度较高、适应性较强的六面体网格。由于近壁面区域有影响流体流动非常重要的速度梯度，因此为了获得更精确的模拟数值解在近壁面区域对网格进行加密处理。

为了检验网格的无关性，对流体c的直管管外降膜流动进行了模拟研究，并在入口流量为10kg·h-1时对近壁面处的网格进行了不同程度的加密处理。通过有限元分析软件计算得到当网格数为28.2万、33.2万、38.3万、43.3万、50万和53万时膜厚值如表2所示，根据公式(10)计算在同等条件下膜厚值的解析解为6.58mm， 又根据绝对误差定义得到表2中误差值，发现当网格数达到43.3万时，膜厚误差在3%以内，因此选择网格数为43.3万的数学模型进行模拟研究。

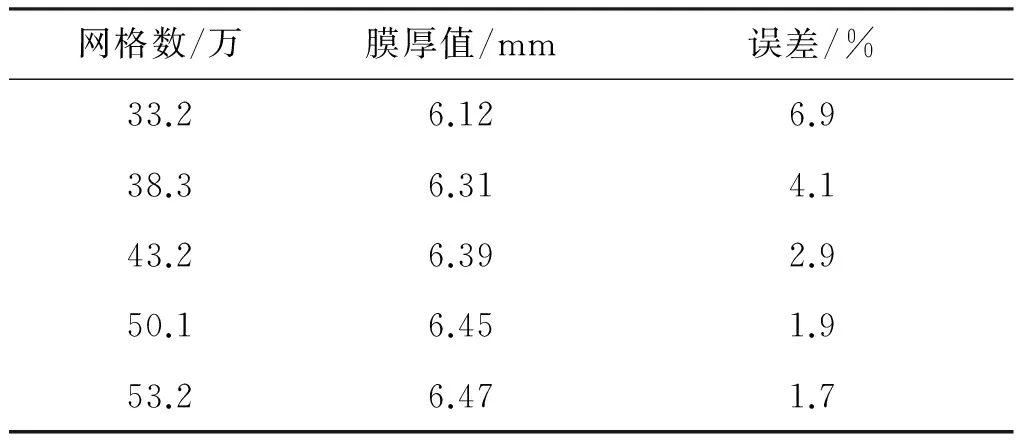
表2 不同网格数下膜厚值与解析解误差分析

2.2 经验公式验证

通过将模拟计算值与解析解进行对比分析可以判断数值模拟的可靠性，从图2可以看出，二维和三维数值模拟所得的膜厚值与解析解相差不大，由于流体沿管外降膜支撑元件是圆柱形或其他复杂结构，而且三维模型更加能反映客观实体，计算结果也与解析解[8]更吻合，因此本文中选择三维模型代替二维模型。

图2 数值模拟结果与经验公式的对比

4 结果与讨论

武晓伟等[9]研究了直管管外降膜流动的膜厚变化，结果表明流体离开入口沿管壁向下发展液膜厚度值迅速减小，减小趋势放缓趋于一定值。图3显示，当流体d在直管管外以5 kg/h和10 kg/h的流量流动时，其自由面变化的趋势与文献9的结果一致，由于成膜通道处流体平均速度较小,惯性力作用小,而黏性力与表面张力无明显变化,导致入口附近膜面收缩严重。但当流量达到15 kg/h和20 kg/h时膜面迅速扩张再缓慢收敛最后趋于一定值。

图3 直管入口处流体相分布图

为了研究直管管外降膜的膜厚与速度分布情况，截取了四种流体液膜达到稳态时的膜厚与平均速度值，结果如图4和图5所示。从图4可以看出，同一流体在降膜过程中液膜厚度随流量的增大而增大，且趋势放缓，这是由于自由降膜过程入口流量越大，惯性力与重力作用越显著，膜面收缩越缓慢。同一流量下，流体黏度越大，作用在流体上的黏性力越大，导致牛顿流体速度减小，膜厚增大。

图4 黏度对管外降膜流动成膜厚度的影响

在不同黏度下，膜面速度与流量的关系如图5所示。液膜表面速度在四种黏度下均随着流体流量的增大而增大，这是因为同一流体流量越大，通过成膜通道的流体的初速度越大，流体膜面速度也越大。同一流量下，流体黏度越低，液膜表面速度越大，这是由流体所受黏性力减小，而惯性力与重力作用力增加导致的。

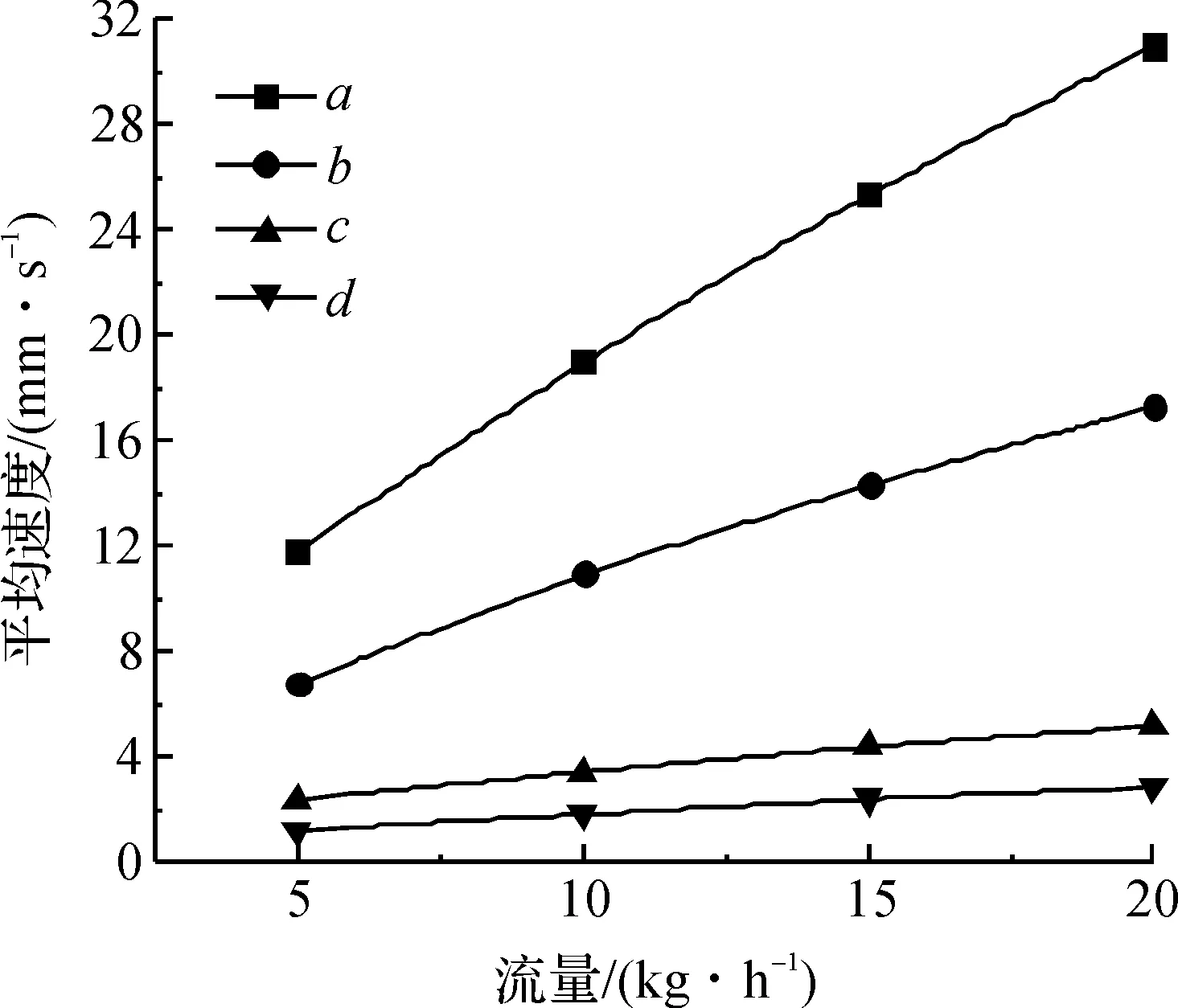
图5 不同黏度下膜面速度随流量的变化

具有特殊壁面结构的降膜元件可以加强液体在降膜过程中的传递性能，因此本文对高黏流体在波管管外降膜过程中的动力学行为也进行了研究。图6和图7反映了在不同参数变化时，液膜自由表面达到稳态在两个完整波节处沿流动方向的变化情况，其中图6是4种流体在15 kg/h时的自由面波动图，而图7是流体c在不同流量下的自由面波动图,从两幅图中可以看出，在不同黏度和不同流量下液膜自由表面均随壁面做相同频率的外凸形波动，但其波动的幅度随着物料黏性和流量的增加均有所减小。

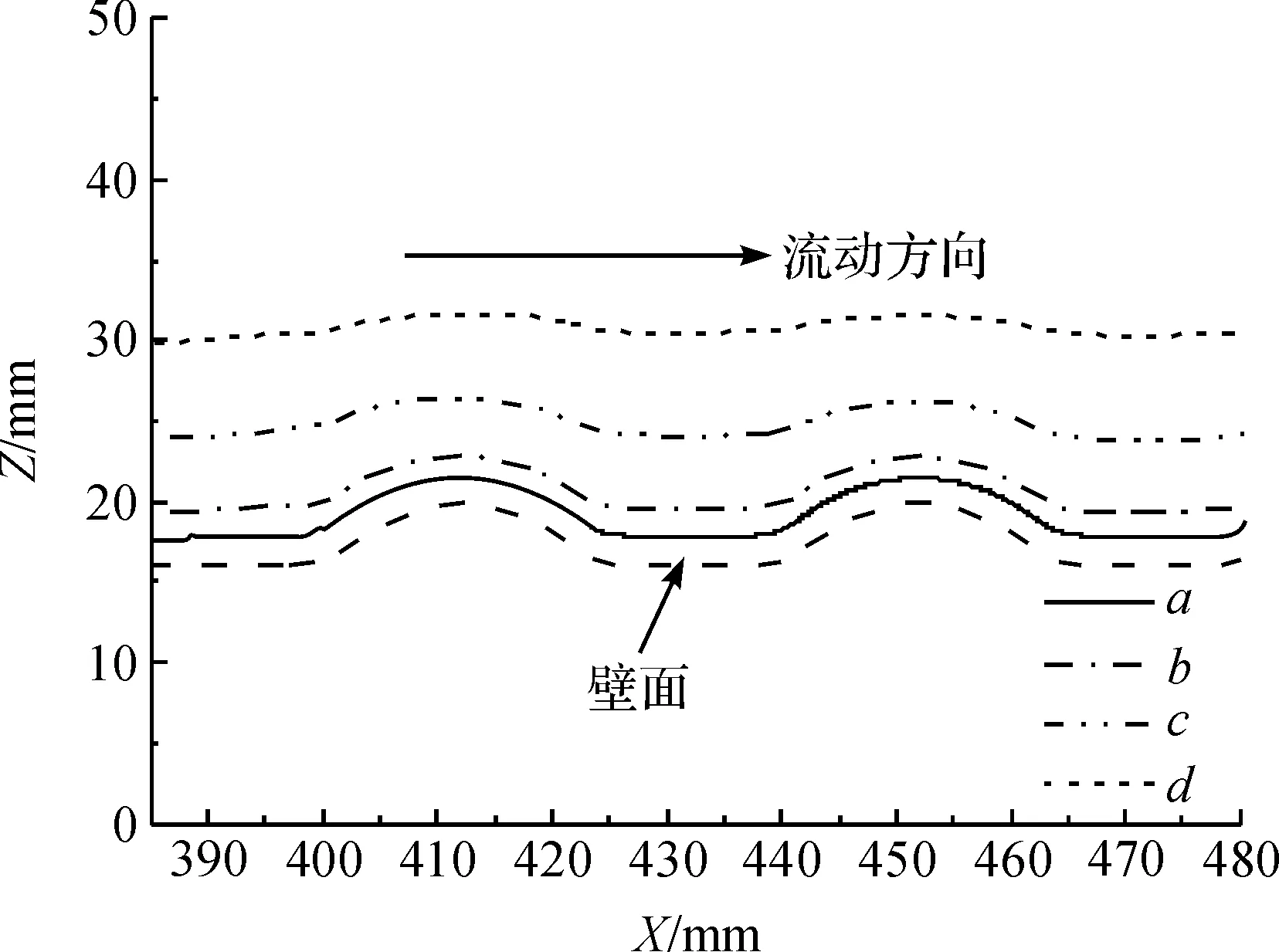
图6 不同黏度流体降膜流动的自由面

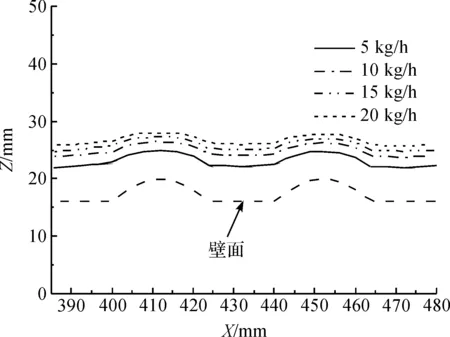
图7 流量对液膜自由表面的影响

流体b在质量流量为15 kg/h时沿波形管外壁流动，其液膜表面速度的变化情况如图8所示,由图可知流体在波节管上的降膜速度变化较为复杂，但总体上随波节呈轴对称分布，并在波峰(B)位置附近达到最大值13 mm/s，在波峰起始(A)与波峰结束位置(C)出现最小值12.2 mm/s。随着波节的凸出流动受到阻碍，流速迅速减小，当流动至AB段阻力明显减小且重力在竖直方向的分量逐渐增大，流速开始增大，最终在黏性力与惯性力的共同作用下流速在波峰附近平稳下来。

图8 波形壁面液膜表面流速的变化

由于波形管外径的周期性变化，导致波形管管外的降膜膜厚分布不均匀，但整体随波形管壁面做周期性的变化，如图9所示，当流体c在不同流量下在波节上流动时，其液膜厚度随流量的增加而增加，且均在波节AC段先减小后增大并在波峰B处膜厚达到最小值，分析可知高黏流体在整个波节上做降膜流动时，在AB段和BC段膜面速度有明显的增大和减小过程，且液膜与降膜管壁面的接触面积先增大后减小，致使其成膜厚度在整个波节处先减小后增大。比较图8和图9发现流体在A、C两点的速度有波动，而膜厚却均匀过渡，这是因为高黏流体在流速发生变化时，由于其黏性力的作用膜厚不会瞬时发生改变。

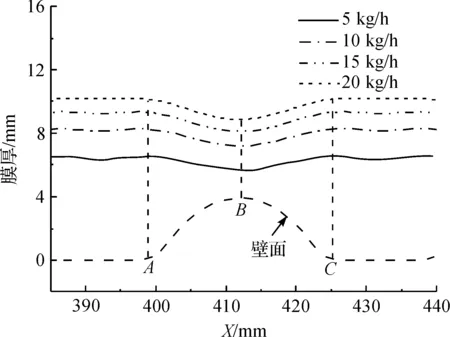
图9 流动方向上液膜厚度的变化

5 结 论

本文利用数值模拟软件对高黏流体在不同降膜元件下竖直管外降膜过程进行了研究，考察了降膜管结构、料液黏度和入口流量等参数对降膜过程的影响，并与解析解做了比较，验证了模拟结果的可靠性，得出以下结论：

a)高黏流体管外降膜流动的三维波动性小，可以通过改变降膜管的壁面结构促进波动，从而强化热质传递性能

b)当高黏流体在波形壁面上降膜流动时，其液膜自由表面随同壁面做相同频率的外凸形波动，且黏度越高波动幅度越小。

本文对高黏流体管外降膜行为进行了三维数值模拟，分析了其流体动力学行为，本文的研究结果为进一步研究高黏流体内部在降膜过程中的传热传质过程的机理提供基础。

[1] NUSSELT W. Die oberflachenkondesation des wasserdamffes the surface condensation of water[J]. Zetrschr Ver Deutch Ing,1916,60:541-546．

[2] MORAN K, INUMARU J, KAWAJI M. Instantaneous hydrodynamics of a laminar wavy liquid film[J]. Internation Journal of Multiphase Flow,2002,28(5):731-755.

[3] GAO D, MORLEY N B, DHIR V. Numerical simulation of wavy falling film flow using VOF method[J]. Journal of Computational Physics,2003,192:624-642.

[4] 马学虎,薄守石,兰忠,等.降液膜波动的影响因素分析[J].高校化学工程学报,2010,24(1):10-15.

[5] LIU S, HAO Y L. Numerical simulation on gas-liquid tow-phase motion of falling film in vertical tube[J], Journal of Thermal Science and Technology,2008,7(1):5-10.

[6] GARCIA A, SALANO J P, VICENTE P G, et al. The influence of artificial roughness shape on heat transfer enhancement: Corrugated tubes, dimpled tubes and wire coils[J]. Applied Thermal Engineering,2011,35(1):196-201.

[7] 王纯,刘艳梅,周涛,等.基于ICEMCFD对汽轮机末级三维叶片流场网格划分方法的优化[J].汽轮机技术,2012,54(5):324-326.

[8] HAN H Z, LI B X, YU B Y, et al. Numerical study of flow and heat transfer characteristics in out ward convex corrugated tubes[J]. International Journal of Heat and Mass Transfer,2012,55(25/26):7782-7802.

[9] 武晓伟,杨建俊,方书起.新型液体管外降膜布膜装置的实验研究[J].化学工程,2013,41(1):20-23.

(责任编辑： 唐志荣)

3D Numerical Simulation of High-Viscosity Falling Film Flow Outside Vertical Tube

WANGFei,CHENShichang,MAJianping,ZHANGXianming,CHENWenxing

(National Engineering Laboratory for Textile Fiber Materials & Processing Technology Zhejiang,Zhejiang Sci-Tech University, Hangzhou 310018, China)

Based on CFD (Computational Fluid Dynamics) technology, VOF method was applied to trace position changes of gas and liquid interface and carry out 3D numerical simulation of falling film flow outside vertical tube. Besides, fluid dynamics behaviors of high-viscosity fluid outside smooth vertical tube and wave tube were investigated, including free surface change, film thickness and velocity distribution. The results show that, the film thickness increased with the increase of viscosity, and the velocity reduced when high-viscosity liquid flowed outside both smooth tube and wave tube under the same flow rate. The film thickness and velocity increased significantly with the rise of flow, for the fluid with the same viscosity. When the high-viscosity fluid flowed outside the smooth tube for certain distance, both the velocity and the film thickness tended to be stable. For falling film flow outside the wave tube, the velocity and the film thickness changed periodically with the wave node. The film thickness reached the minimum, and the velocity reached the maximum near the peak. Instead, the result is contrary near the trough.

falling film flow; numerical simulation; high-viscosity fluid; film thickness; velocity distribution

10.3969/j.issn.1673-3851.2017.07.008

2016-10-01 网络出版日期：2017-01-03

国家重点研发计划项目(2016YFB0303001)

王 飞(1990-)，男，江苏徐州人，硕士研究生，主要从事高黏流体管外降膜数值模拟研究。

陈文兴，E-mail：wxchen@zstu.edu.cn

O357.1

A

1673- 3851 (2017) 04- 0512- 06