单轴旋转捷联惯性导航系统加速度计尺寸误差标定方法

王昆明， 谢建， 周召发

(火箭军工程大学 兵器发射理论与技术国家重点学科实验室， 陕西 西安 710025)

单轴旋转捷联惯性导航系统加速度计尺寸误差标定方法

王昆明， 谢建， 周召发

(火箭军工程大学 兵器发射理论与技术国家重点学科实验室， 陕西 西安 710025)

加速度计尺寸误差在载体角运动情况下，会造成捷联惯性导航系统导航解算误差，这在单轴旋转捷联惯性导航系统中尤为显著。为提高导航精度，提出一种新的加速度计尺寸误差标定方法。通过分析单轴旋转调制下尺寸误差的作用机理，建立导航误差与尺寸误差的数学模型；为进一步提高标定效果，引入加速度计等效误差作为扩展观测量，利用可观测性分析方法设计具体的标定路径，通过滤波获取尺寸误差参数。仿真和实验结果表明，相比仅以速度误差为观测量的方法，该方法可以实现对加速度计尺寸误差的更高精度快速标定，导航速度解算误差可降低约50%.

兵器科学与技术； 旋转调制； 尺寸效应； 扩展观测量； 可观测性分析； 误差标定

0 引言

旋转调制捷联惯性导航系统是一种运用旋转调制技术的新型惯性导航系统，其通过在惯性器件上加装转动机构和测角装置，利用转动机构的旋转功能将误差调制成周期变化的形式，进而在导航解算中采用积分运算法来尽可能消除其影响，最终减少系统误差的累积，保证长时间导航的精度，而无需对惯性元件的漂移误差进行估计[1]。旋转调制技术补偿了惯性器件的常值漂移误差、比例因子对称性误差、不对称性误差以及安装误差等[2]，有效提升了捷联惯性导航精度。然而，旋转调制技术对某些误差有放大作用，如加速度计尺寸效应等。

加速度计尺寸效应，也称为内杆臂误差[3]，是由于受到实际加速度计物理大小和安装位置的限制，其安装敏感点不会位于惯性测量单元(IMU)质心，而是存在一个尺寸误差所导致的。根据刚体转动理论，在角运动中不同点上的加速度各不相同，位置差异会导致比力测量的差异，如果直接将加速度计的输出代入导航算法，在角运动时势必造成导航解算误差，文献[4]指出：在一定振幅下，内杆臂效应造成的导航速度漂移率与振动频率平方呈正比。可见，旋转调制技术引入的角运动会大大激励加速度计尺寸效应，导致严重的导航解算速度误差。因此，对于旋转调制捷联惯性导航系统，除了需进行常规的静态标定外，对加速度计尺寸效应进行补偿也是必不可少的。

对于加速度计尺寸效应的标定补偿，目前国内外学者做了许多研究：文献[5]给出了杆臂效应力学补偿法的模型，并通过实验验证了力学补偿法的可行性；文献[6]分析了内杆臂效应产生的原因，指出进行内杆臂效应补偿的方法是将加速度计敏感点处的加速度测量值折算至它们的敏感轴交点，但其分析是建立在IMU的3个加速度计敏感轴互相垂直并相交于一点比较理想的条件下，使其应用大大受限；文献[7]对内杆臂误差进行了分析与建模，推导出内杆臂误差与导航速度误差之间的数学表达式，通过分析确定了内杆臂长度和振动频率是影响内杆臂误差的2个因素；文献[8]针对加速度计非正交安装情形，从常规静态标定模型出发建立了尺寸效应的误差模型，但未给出具体标定方法；文献[9]分析了单轴旋转产生的加速度计尺寸误差效应，研究了有无阻尼条件下尺寸效应引起的系统导航误差，但同样未给出具体标定方法；文献[10]通过转台匀速转动，以重力加速度为基准对捷联惯性导航系统尺寸效应进行了标定补偿，但此方法需要速率转台及高精度水平基准，对实验条件要求较高；文献[11]建立了导航速度误差与加速度计尺寸误差之间关系的数学模型，设计了多位置转动实验以辨识加速度计尺寸误差参数，但此方法针对的是传统捷联惯性导航系统，对于单轴旋转捷联惯性导航系数未进行具体分析。

针对上述文献的不足，本文根据文献[11]的基本思路，具体分析了单轴旋转调制情况下加速度尺寸效应的作用机理，进而借鉴文献[12]充分利用外部可观测信息进行状态估计的思路，通过引入更多观测信息以提高标定精度，提出了一种将加速度计等效误差作为扩展观测量的单轴旋转调制系统加速度计尺寸误差标定方法，仿真和实验结果表明该方法相对传统方法具有更好的标定效果。

1 误差描述

首先对加速度计尺寸效应误差做具体描述。对于陀螺仪来说，其尺寸效应误差可以忽略，任意安装位置均能实现系统的空间三维角速度测量。然而，加速度计安装敏感点的位置差异会导致比力测量的不同，因此加速度计尺寸效应误差是系统最主要的尺寸效应误差，不能忽略。常规的标定方法主要是静态标定，即利用转台或正交六面体进行多位置静态数据采集和标定处理，得到加速度计的静态标定模型。但是由于尺寸效应只有在载体角运动时才得到激励，使用多位置静态标定法只能确定各加速度计敏感轴的指向，而无法标定尺寸误差。下面在静态标定的基础上，研究加速度计尺寸效应。

非正交安装情况下，各加速度计输出为

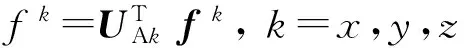
(1)

式中：fk为各加速度计敏感点处的加速度矢量；UAk为各加速度计敏感轴的单位方向矢量。

以x向加速度计为例，已知

(2)

fx=fb+fLx，

(3)

式中：fb为真实加速度；fLx为考虑杆臂效应引入的干扰加速度。

由(1)式和(3)式可知

(4)

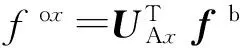
(5)

fox即为载体加速度在x向加速度计敏感轴上的投影，可以通过(5)式对加速度计输出进行补偿，以消除加速度计尺寸效应。

将3个加速度计标定合在一起，写成矢量形式，得

(6)

根据(5)式和(6)式，可以得出载体加速度fb为

(7)

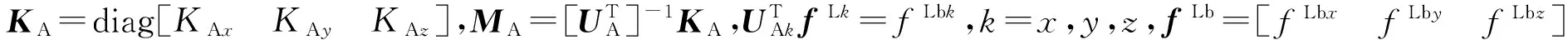
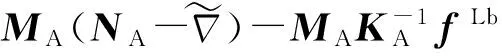
(8)

(8)式给出了非正交安装情况下的尺寸效应补偿公式，式中MA、KA都可以通过加速度计静态标定获取。

2 单轴旋转调制下的加速度计尺寸效应模型

旋转调制捷联惯性导航系统相比固定式捷联惯性导航系统，增加了转位机构，因而其分析方法也相应有所差异，为描述单轴旋转调制下的加速度计尺寸误差，首先定义如下坐标系：

1)导航坐标系(n系)：该坐标系随地球的自转和载体的运动而相对惯性系运动，本文采用东- 北- 天导航坐标系。

2)载体坐标系(b系)：该坐标系与单轴旋转捷联惯性导航系统的基座固联，xb、yb、zb分别指向载体的右方、正前方和上方，构成右手直角坐标系。

3)惯性器件敏感坐标系(s系)：该坐标系的原点位于IMU中心，当转位机构位于转角零位时，s系与b系的对应坐标轴重合。

4)惯性坐标系(i系)：其坐标原点位于地心，相对于惯性空间静止的参考惯性坐标系，其zi轴沿地轴指向北极方向，xi与yi轴在地球赤道平面内，xi与yi、zi构成右手直角坐标系。

加速度计尺寸误差如图1所示。

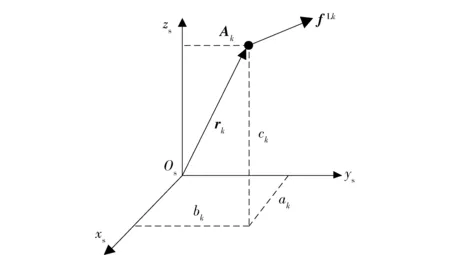
图1 x加速度计尺寸误差示意图Fig.1 Schematic diagram of x accelerometer dimension error

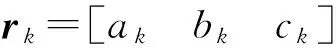
(9)

已知单轴旋转捷联惯性导航系统中：

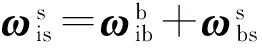
(10)

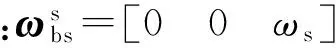
则(9)式可展开为

k=x,y,z.

(11)

根据(7)式，可知s系内有

(12)

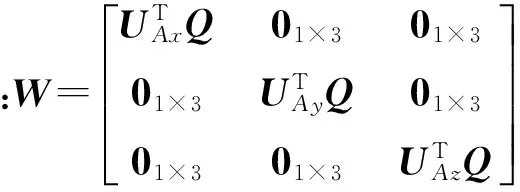
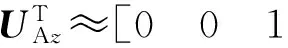
(13)

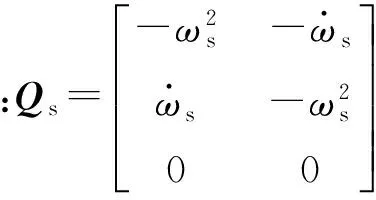
(12)式可简化为

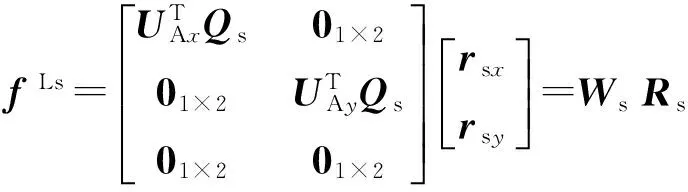
(14)

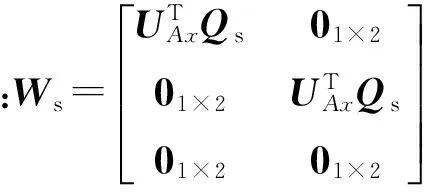
则在s坐标系内，(8)式可表示为

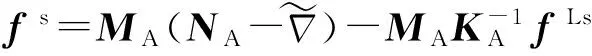
(15)

则fs在载体坐标系内的投影为

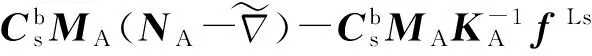
(16)

式中：

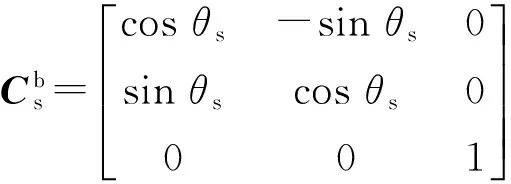
(17)

θs为转位机构转过的角度，可以通过测角机构实时测量给出。

通过计算得到的加速度值为

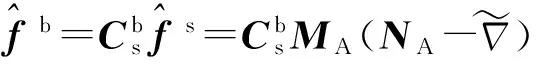
(18)

则加速度测量误差为

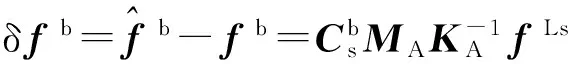
(19)

将(14)式代入(19)式，得

(20)

3 基于扩展观测量的加速度计尺寸误差标定方法

对于加速度计尺寸误差的标定，传统的方法是控制惯性导航系统作角运动，由此产生的加速度计尺寸效应会导致导航速度解算出现相应的误差，根据此误差即可标定出加速度计尺寸误差。

文献[10]中导航速度误差在较短时间内的变化规律为

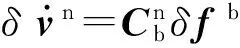
(21)

将(20)式代入(21)式，得

(22)

由此便建立起导航速度误差与尺寸误差参数Rs之间关系的量测方程，可通过最小二乘法或者Kalman滤波法辨识获得尺寸误差参数。

理论上，地球重力加速度仅在天向存在分量，其水平分量应为0 m/s2，然而由于转位机构旋转带来的加速度计尺寸效应，导致加速度计输出折算至导航坐标系下，与地球重力加速度不匹配，即存在等效误差。可见，加速度计等效误差中也包含了加速度计尺寸效应，可将这一分量作为系统观测信息引入Kalman滤波器中。

对比速度误差及加速度计等效误差与加速度计尺寸误差的数学关系，可以看出：导航速度误差是尺寸误差的1阶导数，而加速度计等效误差是尺寸误差的线性函数。因此，相比导航速度误差，加速度计等效误差的可观测性更好。引入加速度计等效误差作为扩展观测量，则可以有效提升加速度计尺寸误差的观测精度和速度，这就是基于扩展观测量的加速度计尺寸误差标定的基本原理。

3.1 状态方程的建立

由于陀螺及加速度计已经过静态标定，这里忽略惯性器件本身误差，只考虑加速度计尺寸效应。根据静基座条件下捷联惯性导航系统的误差模型[12]：

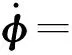
(23)

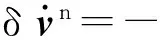
(24)

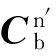
结合第2节推导的加速度计误差模型，可得出捷联惯性导航系统10阶误差状态方程：

(25)

式中：

X=

(26)

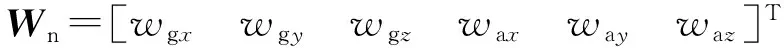
(27)

(28)

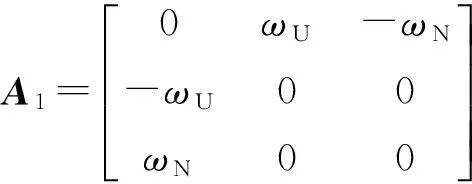
(29)

(30)

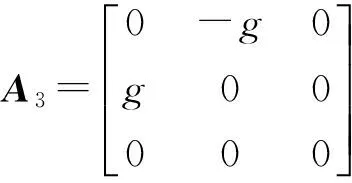
(31)

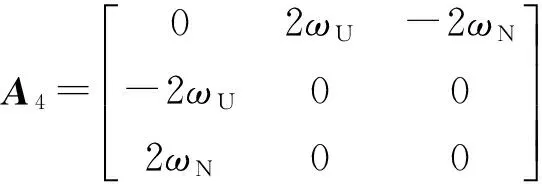
(32)

RM、RN分别为地球子午圈和卯酉圈半径，h为惯性导航系统所在的海拔高度，L为当地地理纬度，g为地球重力加速度大小。

以速度误差为观测量，列写观测方程有

Z1=H1X+v1,

(33)

式中：

(34)

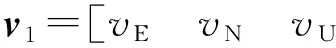
以加速度计等效误差为观测量，已知

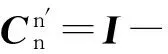
(35)

则加速度计等效误差为

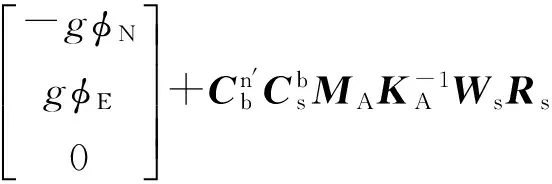
(36)

式中：gn=[0 0gn]T为地球重力加速度矢量在导航坐标系的投影。

列写观测方程有

Z2=H2X+v2,

(37)

式中：

(38)

3.2 基于奇异值分解的可观测度分析

系统的可观测性决定了Kalman滤波对系统误差参数的标定速度和精度，因而建立状态方程后，需要分析系统的状态可观测性，从而设计标定路径。这里采用可观测性矩阵的奇异值分解(SVD)方法来对各参数的可观测度进行分析。SVD方法通过对系统提取可观测矩阵(SOM)进行奇异值分解，求出奇异值大小即可以判断状态量的可观测程度，且不需要事先做Kalman滤波运算即可实现系统可观测度分析[13]。下面采用SVD方法对单轴旋转捷联惯性导航系统进行可观测性分析。

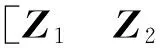
系统误差方程如3.1节所示，地理纬度取为L=34.246°，初始姿态角设置为(5°，5°，25°)。可观测度分析时时间段长度取1 s，设置

当惯性导航系统的转位机构保持静止时，对于两种观测量，都有rank[Qs(1)]=6<10，系统不完全可观，参数ax、bx、ay、by均不可观，这与前面所述的尺寸效应只有在载体角运动时才得到激励相对应。

当惯性导航系统的转位机构匀速旋转时，设角速度为10°/s，计算可知2种观测量对于任意j>1，都有rank[Qs(j)]=8<10，系统不完全可观，参数bx、ay不可观。这也可以由(13)式推导得出：当角加速度为0°/s2时，bx、ay相对应的项近似为0，无法有效观测。

当转位机构变速旋转时，先从静止开始，以角加速度1°/s2转动10 s，再以角速度10°/s匀速旋转。计算2种观测量可知，对于任意j>1，都有rank[Qs(j)]=10，系统完全可观。

表1给出了变速旋转情况下，同一时间段，两种观测量对于加速度计尺寸误差参数的可观测度。

表1 可观测度对比

由表1可见，引入加速度计等效误差作为扩展观测量时，虽然对加速度计尺寸误差参数的可观测性没有显著影响，但是有效提升了误差参数的可观测度，从而对误差参数的估计速度和精度都会得到提高。

3.3 标定方案设计

由3.2节可观测度分析，可以确定如下外场条件下加速度计尺寸误差标定方案：

1)惯性导航系统通电，静置5 min至状态稳定；

2)采集数据200 s；

3)控制转位机构按照匀加速—匀速—匀减速旋转，采集数据600 s.

标定过程数据处理包括以下步骤：

1)静基座对准。利用惯性导航系统静止时采集的前200 s数据进行初始对准；

2)导航滤波估计。对准完转入导航计算，同时进行误差参数滤波估计，标定出加速度计尺寸误差；

3)误差补偿。估计出加速度计尺寸误差后，对惯性导航系统的输出信号进行误差补偿。

4 实验及分析

4.1 仿真标定实验

采用Matlab环境进行仿真标定实验，设置加速度计尺寸误差ax、bx、ay、by均为2.0 mm，其余参数设置与3.2节相同。

分别以两种观测量进行Kalman滤波，两种方法对加速度计尺寸误差的标定结果如图2～图5所示。

图2 ax、bx仿真标定结果对比Fig.2 Comparison of calibrated results of ax and bxin simulation

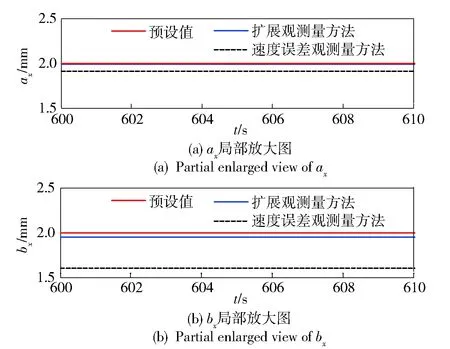
图3 ax、bx仿真标定结果局部放大图Fig.3 Partial enlarged views of ax and bx

图4 ay、by仿真标定结果对比Fig.4 Comparison of calibrated results of ay and by in simulation

由图2～图5可看出，相比速度误差观测量方法，扩展观测量方法的收敛速度更快，且标定精度更高，这与前面理论分析结果一致，说明扩展观测量方法可以有效提升对尺寸误差的标定效果。

4.2 实物标定实验

采用某型单轴旋转捷联惯性导航系统进行尺寸误差标定实验，系统如图6所示。

图6 单轴旋转捷联惯性导航系统Fig.6 Single-axial rotation SINS

根据3.3节中所述的标定方法，分别采用两种观测量方法对加速度计尺寸误差进行标定，标定结果如图7和图8所示。

图7 ax、bx实验标定结果对比Fig.7 Comparison of calibrated results of ax and bx in experiment

图8 ay、by实验标定结果对比Fig.8 Comparison of calibrated results of ay and by in experiment

由标定出的加速度计尺寸误差，根据(14)式和(16)式，以及由测角机构测量的角速度对加速度计输出进行尺寸效应补偿，图9给出了两种方法误差补偿后载体水平速度变化曲线。

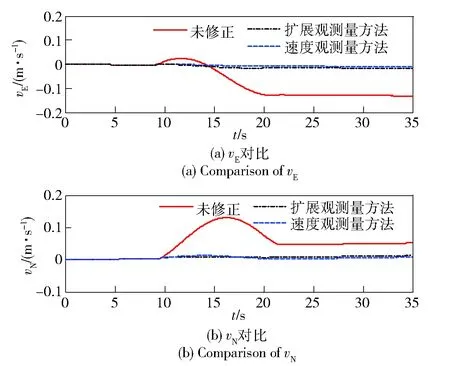
图9 补偿尺寸误差前后的导航速度结果对比Fig.9 Comparison of navigation velocities before and after compensation of dimension error

由图9可以看出，经过补偿修正后，加速度计尺寸效应引起的水平速度变化大大减小，具体结果见表2.

由上述图和表可见，两种补偿方法都能有效补偿由尺寸误差导致的水平速度差，本文提出的扩展观测量方法补偿效果更好，相比传统方法，导航速度误差降低了50%以上，即扩展观测量方法对尺寸误差的标定精度更高。

表2 导航速度误差对比

5 结论

尺寸效应误差是激光陀螺捷联惯性导航系统的一个重要动态误差，本文分析了单轴旋转调制捷联惯性导航系统中加速度计尺寸效应的具体作用机理，建立了导航误差与尺寸误差的数学模型，在此基础上提出了一种将加速度计等效误差作为扩展观测量的单轴旋转调制系统加速度计尺寸误差标定方法，并利用基于奇异值分解的可观测性分析方法设计了标定路径，最后通过仿真及实验验证了标定方法的有效性。实验结果表明：该标定方法可以有效补偿由于加速度计尺寸效应导致的导航误差，相比仅以速度误差为观测量的方法，该方法可以实现对加速度计尺寸误差的更高精度快速标定，导航速度解算误差可降低约50%，具有较强的工程意义。

References)

[1] Lahham J I, Wigent D J, Coleman A L. Tuned support structure for structure-borne noise reduction of inertial navigator with dithered ring laser gyros (RLG)[C]∥Proceedings of IEEE Position Location and Navigation Symposium. San Diego, CA, US: IEEE,2000: 419-428.

[2] 袁保伦. 四频激光陀螺旋转式导航系统研究[D]. 长沙：国防科学技术大学，2007：71-80. YUAN Bao-lun. Research on rotating inertial navigation system with four-frequency differential laser gyroscope[D]. Changsha: National University of Defense Technology, 2008:71-80. (in Chinese)

[3] Titterton D H, Weston J L. Strapdown inertial navigation technology[M]. Stevenage, Hertfordshire, UK: Institution of Electrical Engineers, 2004.

[4] 严恭敏. 捷联惯导系统动基座初始对准及其它相关问题研究

[R]. 西安:西北工业大学, 2008. YAN Gong-min. On SINS in-movement initial alignment and some other problems[R]. Xi’an: Northwestern Polytechnical University, 2008. (in Chinese)

[5] Hong S, Lee M H, Chun H, et al. Experimental study on the estimation of lever arm in GPS/INS[J]. IEEE Transactions on Vehicular Technology, 2006, 55(2): 431-448.

[6] 严恭敏，严卫生，徐德民. 捷联惯性测量组件中内杆臂效应分析与补偿[J]. 中国惯性技术学报, 2008, 16(2):148-153. YAN Gong-min, YAN Wei-sheng, XU De-min. Analysis and compensation on inner lever arm effect of strapdown inertial measurement unit[J]. Journal of Chinese Inertial Technology, 2008, 16(2): 148-153.(in Chinese)

[7] 周冉辉. 舰用高精度激光陀螺惯导内杆臂误差分析及补偿方法研究[J]. 舰船科学技术, 2016, 38(4):120-123. ZHOU Ran-hui. Rotating scheme designing for two-axis rotating laser gyro inertial navigation system[J]. Ship Science and Technology, 2016, 38(4): 120-123. (in Chinese)

[8] 梁茂柱, 王超, 杜鹏程. 单轴旋转引起加速度计尺寸效应误差分析及补偿[J]. 弹箭与制导学报, 2013, 33(1):179-181. LIANG Mao-zhu, WANG Chao, DU Peng-cheng. Compensation and analysis on size effect error of accelerometers of INS caused by single-axial rotation[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2013, 33(1): 179-181. (in Chinese)

[9] 吴文启, 杨伟光, 杨杰. 激光陀螺捷联惯导系统尺寸效应参数标定与优化补偿[J]. 中国惯性技术学报, 2009, 17(6):636-642. WU Wen-qi, YANG Wei-guang, YANG Jie. Calibration and optimal compensation for size effect parameters of laser gyro SINS[J]. Journal of Chinese Inertial Technology, 2009, 17(6): 636-642. (in Chinese)

[10] 严恭敏, 周琪, 翁浚, 等. 捷联惯导系统内杆臂补偿方法及试验[J]. 宇航学报, 2012, 33(1):62-67. YAN Gong-min, ZHOU Qi, WENG Jun,et al. Inner lever arm compensation and its test verification for SINS[J]. Journal of Astronautics, 2012, 33(1): 62-67. (in Chinese)

[11] 王立冬, 蔡玲. 车载捷联惯导系统静止条件下的初始对准方法研究[J]. 中国惯性技术学报, 2004, 12(2):1-5. WANG Li-dong, CAI Ling. Initial alignment method of SINS in stationary state[J]. Journal of Chinese Inertial Technology, 2004, 12(2): 1-5. (in Chinese)

[12] 秦永元. 惯性导航[M]. 北京:科学出版社, 2006: 35-37. QIN Yong-yuan. Inertial navigation[M]. Beijing: Science Press, 2006: 35-37. (in Chinese)

[13] 刘准, 陈哲. 条件数在系统可观测性分析中的应用研究[J]. 系统仿真学报, 2004, 16(7):1552-1555. LIU Zhun, CHEN Zhe. Application of condition number in analysis observability of system[J]. Journal of System Simulation, 2004, 16(7): 1552-1555. (in Chinese)

Calibration Method of Dimension Error of Accelerometer in Single-axial Rotation SINS

WANG Kun-ming, XIE Jian, ZHOU Zhao-fa

(State Key Discipline Laboratory of Armament Launch Theory and Technology, Rocket Force University of Engineering, Xi’an 710025, Shaanxi, China)

Accelerometer dimension error leads to navigation velocity error under the carrier angular movement in strapdown inertial navigation system (SINS). This is particularly significant in single-axial rotation SINS. In order to improve the navigation accuracy, a new method is presented to realize the calibration of accelerometer dimension errors. A mathematical model of navigation and dimension errors is established by analyzing the mechanism of action of dimension errors in rotary condition. The equivalent errors of accelerometers are introduced into system as extended measurements to improve calibration effect. A calibration route is designed by observability analysis. The dimension error parameters are acquired by filtering. The simulated and experimental results show that the proposed method has higher calibration accuracy and speed compared with the method that uses speed error as observed quantity, and the amount of navigation velocity errors is decreased by about 50%.

ordnance science and technology; rotary modulation; dimension effect; extended measurement; observability analysis; error calibration

2016-11-03

国家自然科学基金项目(41174162)

王昆明(1988—)，男，博士研究生。E-mail:984088528@qq.com

谢建(1967—)，男，教授，博士生导师。E-mail:467040646@qq.com

TJ765.2+31

A

1000-1093(2017)07-1314-08

10.3969/j.issn.1000-1093.2017.07.009