灌封材料对侵彻过载下弹载器件的防护分析

徐萧， 高世桥， 牛少华， 申丽， 刘海鹏， 欧卓成

(1.北京理工大学 机电学院， 北京 100081； 2.中国兵器工业导航与控制研究所， 北京 100089)

灌封材料对侵彻过载下弹载器件的防护分析

徐萧1， 高世桥1， 牛少华1， 申丽2， 刘海鹏1， 欧卓成1

(1.北京理工大学 机电学院， 北京 100081； 2.中国兵器工业导航与控制研究所， 北京 100089)

为研究在灌封材料缓冲保护下弹载器件对冲击载荷的动态响应，利用LS-DYNA用户材料自定义程序UMAT二次开发平台，编写朱- 王- 唐(ZWT)非线性黏弹性本构模型的材料子程序，并将ZWT模型应用于弹体内部灌封材料的动态仿真。通过调整ZWT模型的非线性弹性模量、低应变率Maxwell单元的弹性常数、高应变率Maxwell单元的弹性常数、高应变率Maxwell单元的松弛时间和材料密度，得出不同参数对应下，弹体内部电子器件不同的动力学响应，并分析灌封材料各参数变化对于弹体内部电子器件响应造成的影响。研究结果表明：当非线性弹性模量、低应变率Maxwell单元的弹性常数、高应变率Maxwell单元的松弛时间和材料密度的数值降低时，灌封材料的减振和防护效果更佳。根据仿真结果提出了针对不同工程需求的材料优化方案。

兵器科学与技术； 非线性黏弹性模型； 电子器件； 数值仿真

0 引言

侵彻过载具有强振动和高冲击的特点，弹载电子器件在这种恶劣工作环境很容易失效和损坏[1-4]，因而需要采用适当的封装方法来缓解电子器件承受的冲击。目前研究和应用的抗冲击过载封装技术有4种：灌封防护技术、底部充胶、结构设计和电子设备选择[5]，其中结构设计和灌封防护技术是两大主要研究技术。

针对结构设计来讲，主要目的是通过广泛建模方法，研究冲击载荷是通过何种路径最终传递到关键电子器件上，然后在此研究基础上，设计整体结构来降低最终作用到弹载电子器件上的冲击作用力。Chakka等[6]设计了一种用来承载电子封装的碳纤维增强环氧基质平板，并通过参数分析法研究基板的厚度和碳纤维体积分数变化对电子封装所承受的加速度和应力的影响规律，对真实弹体结构设计提供了有效的理论支撑和帮助。尹威华等[7]设计了一个兼有泡沫材料缓冲和高分子材料灌封的火炮弹载电路模块的缓冲防护结构，利用iSIGHT与ABAQUS的联合仿真，对缓冲防护模块进行了结构参数优化，优化后的测试电路防护结构将最大应力降低了65.1%，具有一定的参考价值。

对于灌封防护技术来说，灌封防护材料的作用主要有两点：1)给嵌入其中的器件提供结构支撑；2)作为被保护组件的减振机构，吸收和耗散掉传递到电子器件上的机械能[8]。

目前用作弹载电子器件防护的材料主要有泡沫金属和高分子材料两种。由于泡沫金属在压缩过程中有高而宽的应力平台，在压缩过程中大量能量在近似恒应力环境下被吸收。卢剑平等[9]设计了一种泡沫铝填充铝壳的组合件作为电子设备的缓冲装置，采用ANSYS/LS-DYNA模拟空气炮子弹撞击电子仪器时泡沫铝和铝壳组合件的响应并分析其吸能效率，但由于组合件有一定的抗压强度，只能够对特定g值范围的冲击有效缓冲，对低g值冲击的缓冲作用较小。

高分子材料因为其具有抗冲击、密封防水和缓冲吸能的特性，被用作大多数弹载电子元器件的灌封材料，此类材料本身的黏弹性效应是其能够吸能缓冲的重要原因。焦敏等[10]研究了在弹体侵彻成层靶体过程中，受线黏弹性灌封材料防护的弹载元器件的动态响应，并分析了灌封材料的黏性、密度和模量对于侵彻过程中弹载元器件响应的影响，从而为灌封材料的优化提供依据。但简单线黏弹性模型不能较完整地描述高分子材料在高速冲击环境下的力学性能，唐志平等[11]系统地研究了高分子材料的非线弹性、黏性和应变率效应等特性，并且在此基础上建立了朱- 王- 唐(ZWT)非线性黏弹性本构模型。冯震宙等[12]和Ahmed等[13]根据ZWT模型编写出与其对应的LS-DYNA用户自定义材料子程序，用来模拟飞鸟撞击飞机风挡玻璃的冲击过程，仿真结果能够很好地与实验结果吻合。

本文在上述文献的基础上，针对一种引信结构，利用LS-DYNA的UMAT接口，采用ZWT非线性黏弹性本构来描述弹载用灌封材料，在典型的侵彻过载条件下，调整灌封材料的不同模型参数进行仿真，根据仿真结果的分析对比来确定ZWT模型不同参数对于灌封材料缓冲效果的影响，进而为工程实用选材提供理论依据。

1 UMAT用户自定义程序

1.1 ZWT本构模型

朱兆祥、王礼立和唐志平等针对典型工程塑料进行了一系列实验研究，发现在冲击载荷下必须考虑材料的率响应特性，高应变率会明显改变材料的本构关系、提高材料的瞬时极限强度，同时也提高材料的屈服应力、扩大弹性范围等力学性能，通过其在不同应变率下的应力行为研究，构筑了ZWT本构方程[14]，即

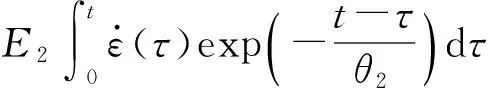
(1)

式中：ε为应变；σ为应力；t为某恒定应变率下加载应变达到ε时的时间；τ为积分自变量；等号右式前3项描述非线性弹性平衡响应，E0、α和β为对应的弹性常数；第1个积分项描述低应变率下的粘弹性响应，E1和θ1分别是所对应的低频Maxwell单元的弹性常数和松弛时间；第2个积分项描述高应变率下的粘弹性响应，E2和θ2分别是所对应的高频Maxwell单元的弹性常数和松弛时间。

1.2 UMAT自定义子程序开发

美国LSTC公司的用户子程序UMAT可以使用户对程序进行用户化，以适应某些特殊需要，使程序具有标准版本所不具备的某些功能。LSTC公司提供了专用于用户二次开发的动态链接库LSDYNA.LIB，连同用户编写的三维增量形式材料子程序一起在Fortran中编译使用。用户编译成功后，生成新的可执行文件LSDYNA.EXE，并将其放入LS-DYNA的安装目录下，之后在LS-DYNA求解界面中选中新生成的可执行文件作为求解器来进行计算。在计算过程中，前一时刻得到的应力增量、应变增量被传递到子程序中，根据增量法计算应力增量，在子程序结束前将应力增量累加，得到当前时刻的单元应力并返回主程序。

当仿真计算中需要调用材料子程序时，在k文件的材料模型定义部分输入关键字*MAT_USER_DEFINED_MATERIAL_MODELS来定义用户材料参数，如弹性模量、泊松比、密度、黏性系数等。用户可以通过subroutine umat41～subroutine umat50最多同时定义10个材料子程序，程序中材料参数的个数和位置需要与*MAT_USER_DEFINED_MATERIAL_MODELS之间的协议一致。当材料模型为正交各项异性材料时，程序中的材料参数数组cm()长度不能超过40，其余模型则不限长度。在材料关键字*MAT中，模型参数从关键字的第3行开始输入，在计算过程中，子程序从关键字中调取材料参数来进行计算。用户自定义的历史变量数组hsv()，可以用来存储计算中间值，在下一次重新进入用户子程序时，程序可以使用这些信息来进行下一步计算。

在编写子程序时关键在于将应力应变关系扩展成三维状态，进而表示成增量形式，最后再用Fortran语言编写编译链接，将子程序算法嵌入到LS-DYNA算法主程序中。

本文采用现时Kirchhoff应力张量Sij和现时Green应变张量εij，将ZWT本构方程(1)式推广至三维状态[15]：

(2)

式中：4阶张量Aijkl为三维各项同性弹性矩阵，

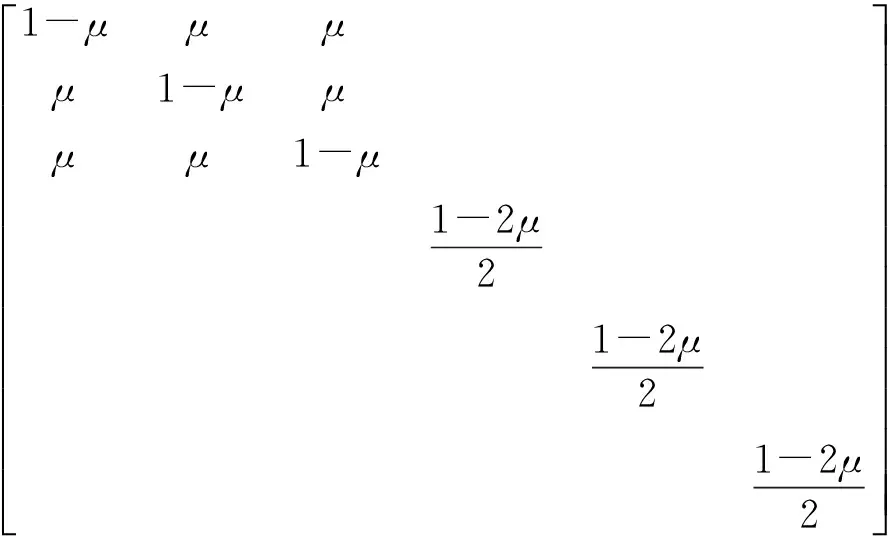
(3)

μ为泊松比。

基于Updated Lagrangian增量迭代法，现时Kirchhoff应力张量Sij的增量形式可表示为

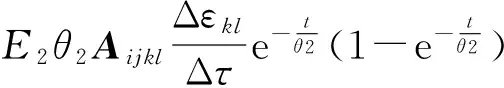
(4)

于是可以得到在时间增量步长的应力递推关系为

(Sij)n+1=(Sij)n+(ΔSij)n.

(5)

1.3 灌封材料的ZWT模型参数

工程中较为常用的灌封材料为环氧树脂，根据文献[16-17]的实验方法，通过准静态压缩实验和Hopkinsion压杆实验，分别测得环氧树脂在应变率为0.000 618 s-1、0.007 69 s-1和2 787 s-1情况下的真实应力- 应变曲线，然后根据最小二乘法拟合出环氧树脂材料的ZWT模型参数，如表1所示，表中ρ为材料密度。

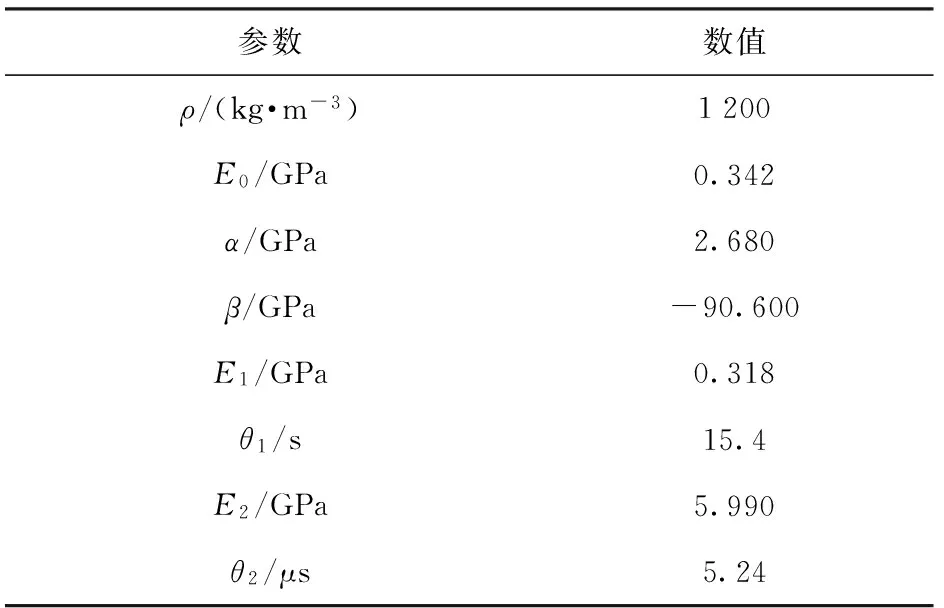
表1 环氧树脂ZWT模型参数

1.4 ZWT本构模型验证

为验证ZWT本构模型对于环氧树脂力学行为描述的可行性，建立如图1所示的标准单轴压缩有限元模型，利用所编程序计算该模型在单轴压缩作用下的响应，不同应变率下仿真和实验数据对比结果如图2所示，二者吻合良好。

图1 单轴压缩有限元模型Fig.1 Finite element model of uniaxial compression

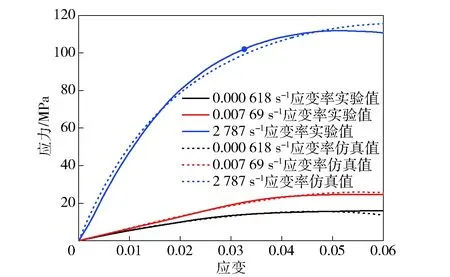
图2 不同应变率下的仿真与实验值对比Fig.2 Simulated and test values at different strain rates

2 引信有限元模型

2.1 建模

图3(a)所示为某典型引信结构，分前、后两个腔室，图3(a)中a为加载的加速度，v为设定的初速度。头部腔室放置加速度计，尾部腔室内放置电路控制系统，电路壳体内部前后放置5个PCB板，各板之间用螺柱连接，固定于引信内壁，在每个电路板中央位置放置一块质量块负载。由于加速度计需要准确测定过载加速度数据，因此头部腔室不需要灌封材料的填充。为保证电路系统能够正常工作，尾部腔室需用缓冲和灌封材料来吸收过载冲击，本结构用成型固态橡胶垫包裹电路系统外壳减少冲击，在壳体内部的其余空腔用环氧树脂灌封材料进行填充密封。为节省计算机时，用1/2模型进行建模，采用八节点六面体单元，网格划分如图3(b)所示。

图3 引信结构图和网格划分图Fig.3 Structure and finite element mesh of fuze

除灌封材料用UMAT编写的非线性黏弹性模型之外，引信壳体、加速度计和电路壳体选用Plastic-Kinematic模型，模型参数如表2所示，E为弹性模量，σy为屈服应力，Et为切线模量。

表2 Plastic-Kinematic模型参数表

内部的元器件如PCB板、电子器件和连接螺柱选用弹性模型，模型参数如表3所示。

表3 弹性模型参数表

包围引信壳四周的超弹性橡胶材料选用Mooney-Rivlin模型，模型参数如表4所示，表中A和B是应变能密度函数常数。

表4 橡胶模型参数表

2.2 加载条件

为简化计算，给引信结构轴向施加300 m/s的初速，将常规实验中加速度计所得的过载数据直接加载到与加速度计相接的引信壳体前端面节点上，方向与速度方向相反，加载条件如图3(a)所示，过载曲线如图4所示。

图4 端面加载曲线Fig.4 Loading curve

2.3 约束条件

考虑引信实际设计安装过程，引信各个部件之间的接触定义如表5所示。加速度计通常用螺纹紧固在引信外壳上，在侵彻过程中不会发生相对位移；填充电路系统的灌封材料在固化之后，和电路外壳内壁以及腔室内部的电路元器件如PCB板、电子器件和连接螺柱之间会紧密粘结在一起，亦不会发生相对位移；螺柱和PCB板、负载元器件和PCB板之间分别由螺纹和焊点固接，接触面间同样不会发生相对位移。因此上述3种情况均选用固联接触Contact_Tied_Surface_To_Surface_Offset.

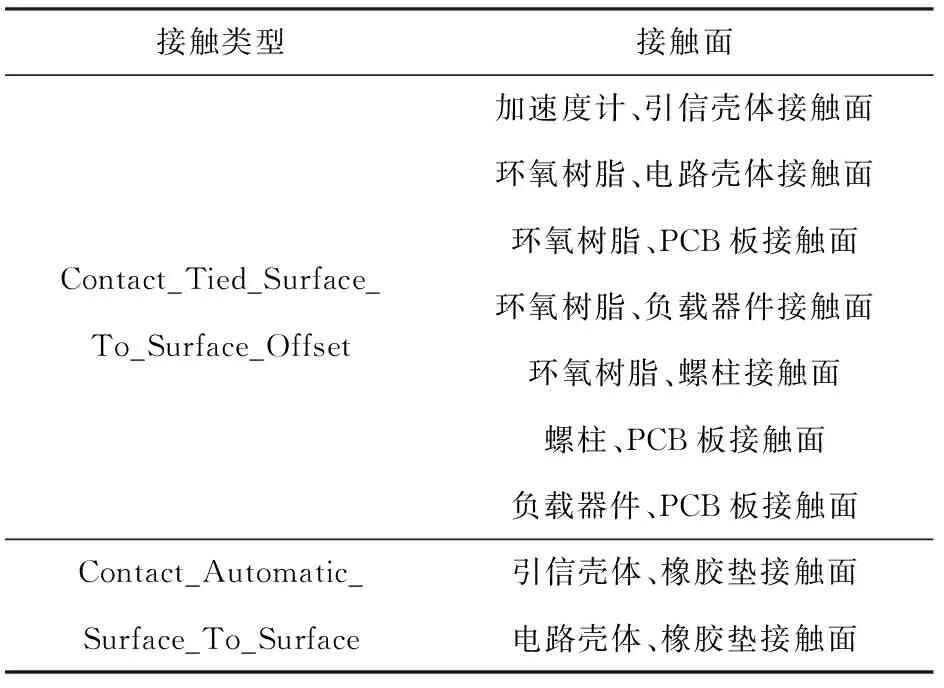
表5 接触定义表

因为尾部的电路系统需要方便从引信壳体中取出，因此仅在引信壳体和电路系统外壳之间放置一层橡胶垫来填充缝隙和缓冲，在这三者之间选用自动面面接触Contact_Automatic_Surface_To_Surface.

3 计算结果与分析

3.1 计算工况

为研究ZWT非线黏弹性模型各个参数对于缓冲效果的影响，在原有材料模型基础上，依次调整模型参数大小，进而分别模拟引信结构的结构响应。为避免浪费机时，在冲击小变形的环境下，将各项参数对计算结果的影响进行预估分析，进而确定计算对比方案。

ZWT非线性黏弹性模型的非线性弹性常数E0为0.342 GPa、α为2.680 GPa、β为-90.600 GPa，当应变为0.01时，弹性项应力值为σe|ε=0.01=E0ε+αε2+βε3=0.003 597 4 GPa.

令α取原值的2倍和0.5倍，当应变为0.01时，弹性项的应力分别为σe|ε=0.01=E0ε+2αε2+βε3=0.003 865 4 GPa，σe|ε=0.01=E0ε+0.5αε2+βε3=0.003 463 4 GPa，较原应力分别增加了7.4%、减少了3.7%，α的改变对于应力幅值影响有限。

令β取原值的2倍和0.5倍，当应变为0.01时，弹性项的应力分别为σe|ε=0.01=E0ε+αε2+2βε3=0.003 506 8 GPa，σe|ε=0.01=E0ε+αε2+0.5βε3=0.003 642 7 GPa，较原应力分别减少了2.5%、增加了1.3%，β的改变对于应力幅值影响同样有限。

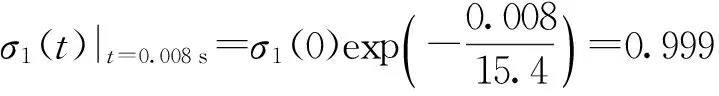
综上所述，因为ZWT材料模型中的α、β和θ1对于仿真计算来说影响较小，因此在本文中不做考虑，不同工况的ZWT模型参数如表6所示。

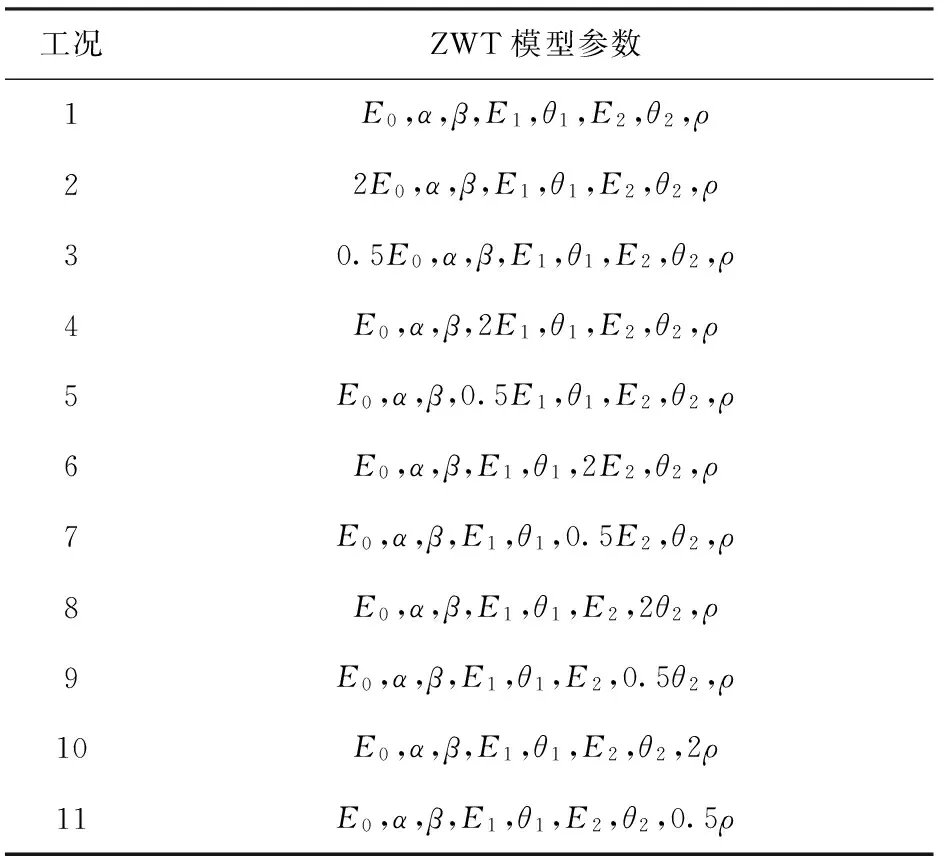
表6 计算工况表

3.2 结构响应分析

图5 结构应变云图Fig.5 Contour of z-strain

从横向角度分析计算结果，可以初步得出一些结构本身对电子器件动力学响应的定性结论，现以工况1为例进行分析说明。

由于橡胶垫的强度较低，在冲击加载过程中会发生较大变形，如图5所示，且由于惯性作用电路系统整体会向前挤压，使得橡胶垫与电路壳体末端及引信壳体之间产生缝隙，从而引起这三者自由面之间的二次碰撞，离末端最近的5号PCB板受到的影响最大。上述原因最终使得电路壳体及其内部器件相对引信外壳产生前后震荡，造成内部器件的刚体加速度值在原始激励的基础上产生叠加。且在后期阶段，虽然端面施加的过载已趋于0g，但是因为橡胶在受压之后会发生回弹的超弹特性，前期受压变形的橡胶垫会推动电路系统在引信腔体内部来回震荡。

此外，由于高分子材料的波阻抗较金属波阻抗小，侵彻初期冲击波在金属外壳中传递的速度要比在灌封材料内部快很多，如图6(b)所示。当冲击波到达引信壳末端之后会发生反射，从引信尾端向前传递，如图6(d)所示，导致距离加载端最远的5号电路板和5号负载受到一个与过载加载方向相反的冲击作用力。

由于对引信结构施加的是轴向的负载，没有对径向施加负载，而在整个过程中径向的响应很小，且引信结构比较对称，整个响应过程中PCB板亦没有发生弯曲变形，各PCB板各处的响应差别很微弱。因此在分析电子器件的加速度过载时，选取整体的刚体加速度为代表，来分析结构的动态响应规律。

各PCB板轴向刚体加速度随时间变化曲线如图7所示，轴向刚体加速度幅值范围如图8所示。从图7中可以看出，PCB板的刚体加速度前期峰值明显大于加载曲线的加速度峰值，振动叠加效应十分明显；且5号PCB板加速度数据在侵彻初期有一个10 000g的反向脉冲；在后期震荡阶段，虽然加载曲线的数值已趋于0g，电子器件的刚体加速度仍在零值前后小幅震荡；这几个现象均与上文的分析相吻合。从图8中可以看出1号PCB板承受的加速度幅值最小，5号PCB板承受的加速度幅值最大。

除了观察刚体加速度外，选取1号～5号负载的中心位置单元为观察对象，各个单元等效应力随时间变化曲线如图9所示，各个单元等效应力最大值如图10所示。可以看出每个负载单元等效应力在后期都有所增加，尤其5号负载的后期等效应力最大，这皆是由于橡胶垫回弹推动电路系统在引信空腔内部前后震荡导致，且5号负载距离末端最近，受到自由面撞击最为严重，此现象与上文分析内容相吻合。1号负载和5号负载中心的等效应力值最大，这是因为冲击波从引信壳体最先传递到1号板和5号板，而中间部分的2号、3号和4号板相较于1号和5号被更多的环氧树脂所保护，冲击波在传递过程中被吸收掉了很大一部分能量，最终导致2号、3号和4号负载所承受的冲击要小很多。

3.3 仿真数据对比及ZWT参数影响分析

根据3.2节分析结果，1号PCB板的刚体加速度最小，5号PCB板的刚体加速度最大；1号负载中心单元和5号负载中心单元的等效应力最大。因此每个工况提取最上1号和最下5号两个PCB板的刚体加速度值和相应板上负载中心位置单元的等效应力数据来进一步分析。

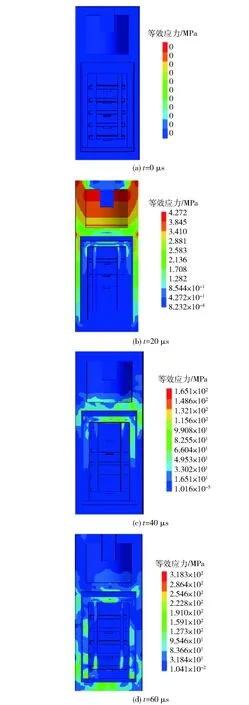
图6 结构等效应力云图Fig.6 Contours of equivalent stress

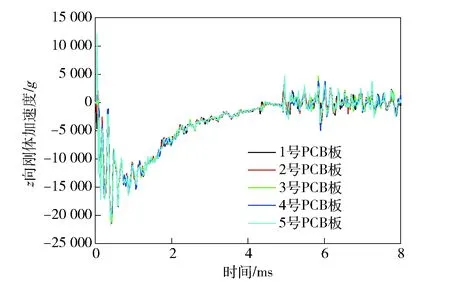
图7 PCB板的z向刚体加速度时间曲线Fig.7 z-rigid body acceleration vs. time for PCBs

图8 各PCB板的刚体加速度幅值范围Fig.8 z-rigid body acceleration amplitudes of five PCBs

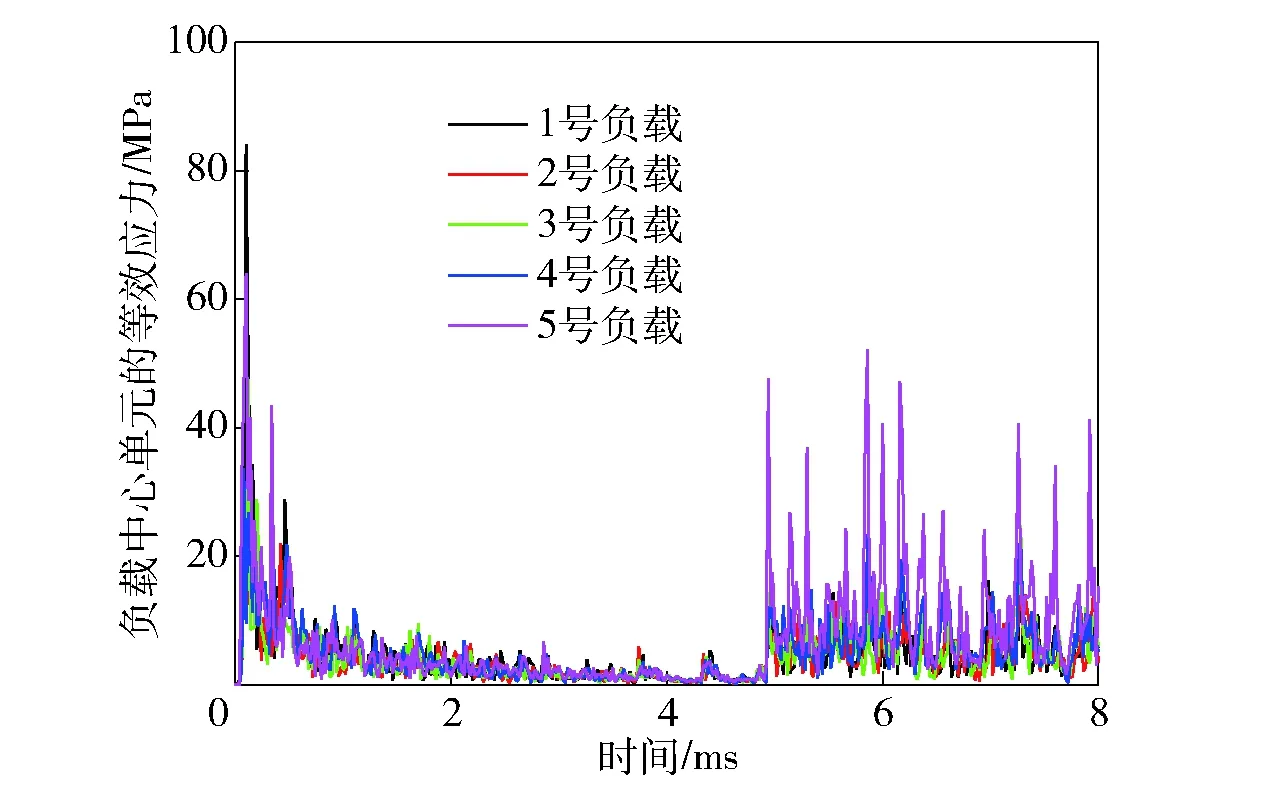
图9 负载中心单元等效应力时间曲线Fig.9 Equivalent stress vs. time for central elements

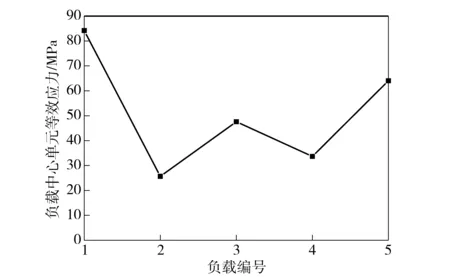
图10 各中心单元的最大等效应力Fig.10 Maximum equivalent stress for each central element

3.3.1 参数E0的影响

图11～图14分别给出了1号和5号PCB板的轴向刚体加速度及中心单元等效应力随参数E0的变化规律。1号和5号PCB板的轴向刚体加速度数据如图11和图12所示，随着E0的减小，两个PCB板的加速度只在侵彻后期振动阶段的频率和幅值有明显的降低；1号负载中心单元的等效应力幅值在整个侵彻阶段都有明显降低，5号负载的中心单元在侵彻前期衰减较大，但后期震荡阶段衰减程度较弱。

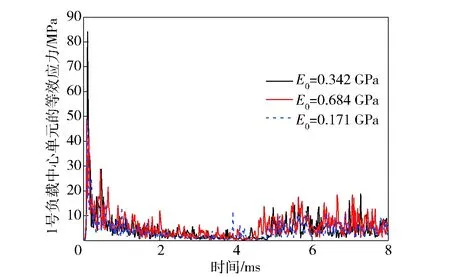
图13 1号负载中心单元的等效应力Fig.13 v-m stress of payload 1’s center element

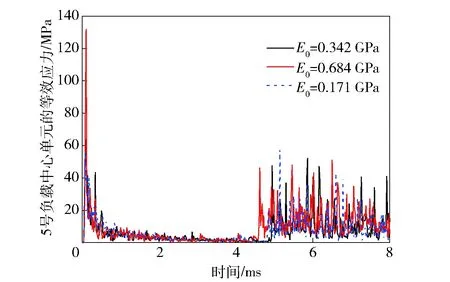
图14 5号负载中心单元的等效应力Fig.14 v-m stress of payload 5’s center element

3.3.2 参数E1的影响

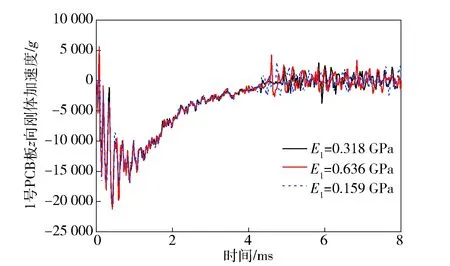
图15 1号PCB板的z向刚体加速度Fig.15 Acceleration of PCB 1’s z-axis rigid body

图16 5号PCB板的z向刚体加速度Fig.16 Acceleration of PCB 5’s z-axis rigid body

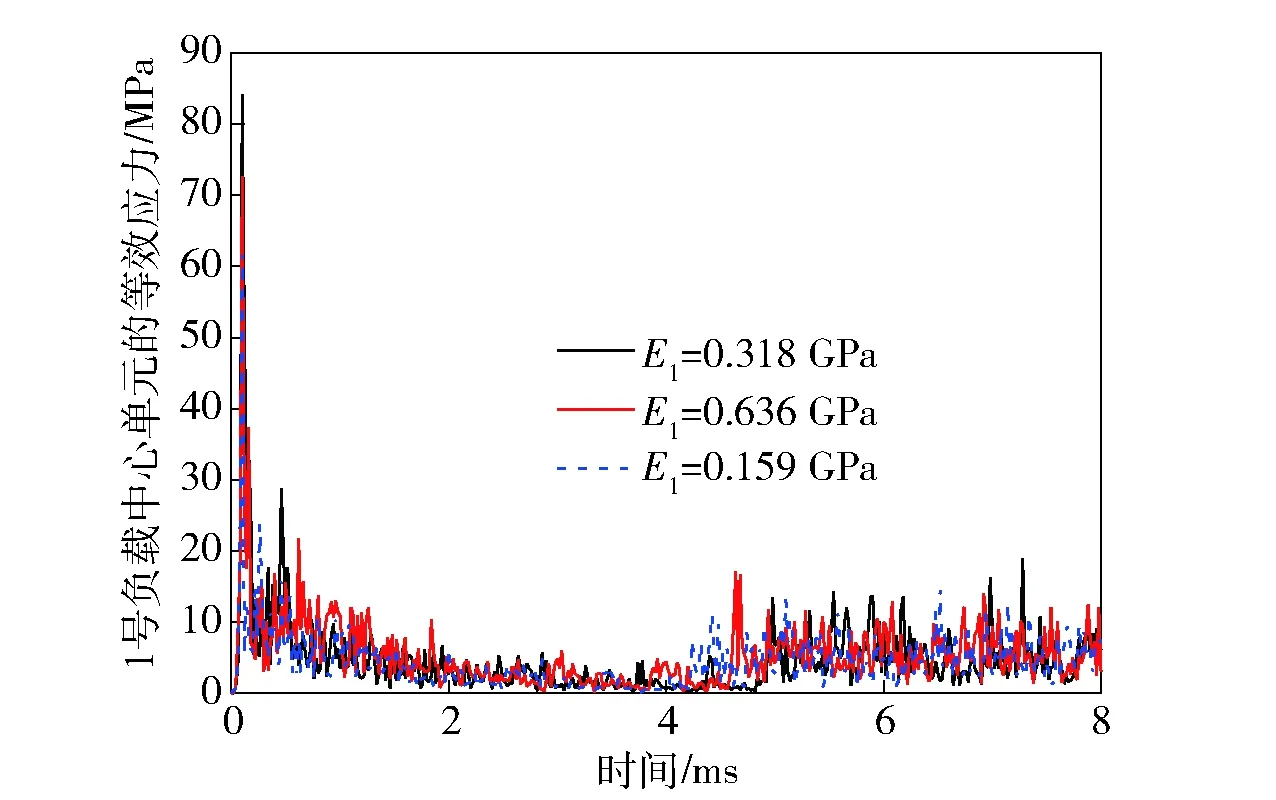
图17 1号负载中心单元的等效应力Fig.17 v-m stress of payload 1’s center element

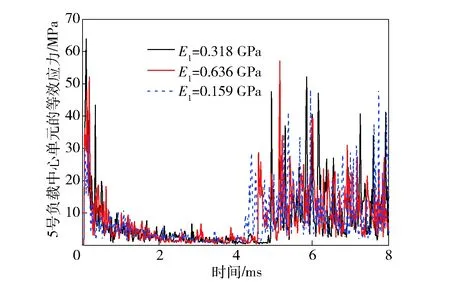
图18 5号负载中心单元的等效应力Fig.18 v-m stress of payload 5’s center element

图15～图18分别给出了1号和5号PCB板的轴向刚体加速度及中心单元等效应力随参数E1的变化规律。从图15～图18中所示数据来看，随着E1减小，1号和5号PCB板的加速度在侵彻前期的幅值有相对明显的降低，而后期振荡阶段虽然最高峰值有所减少，但是整体幅值衰减不明显。1号和5号负载中心单元等效应力的幅值在侵彻前期有明显减小，但是在后期振荡阶段，衰减程度十分微弱。

3.3.3 参数E2的影响

图19～图22为1号和5号PCB板的刚体加速度及中心单元等效应力随参数E2的变化规律。可以看出，从侵彻前期到侵彻后期，无论幅值还是振荡频率，不管E2增大还是减小，均没有明显的改变。

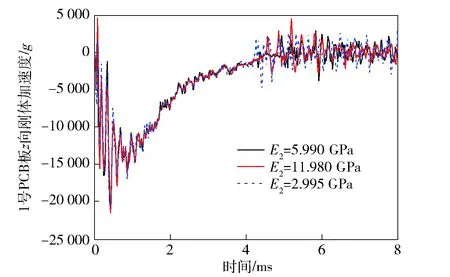
图19 1号PCB板的z轴刚体加速度Fig.19 Acceleration of PCB 1’s z-axis rigid body

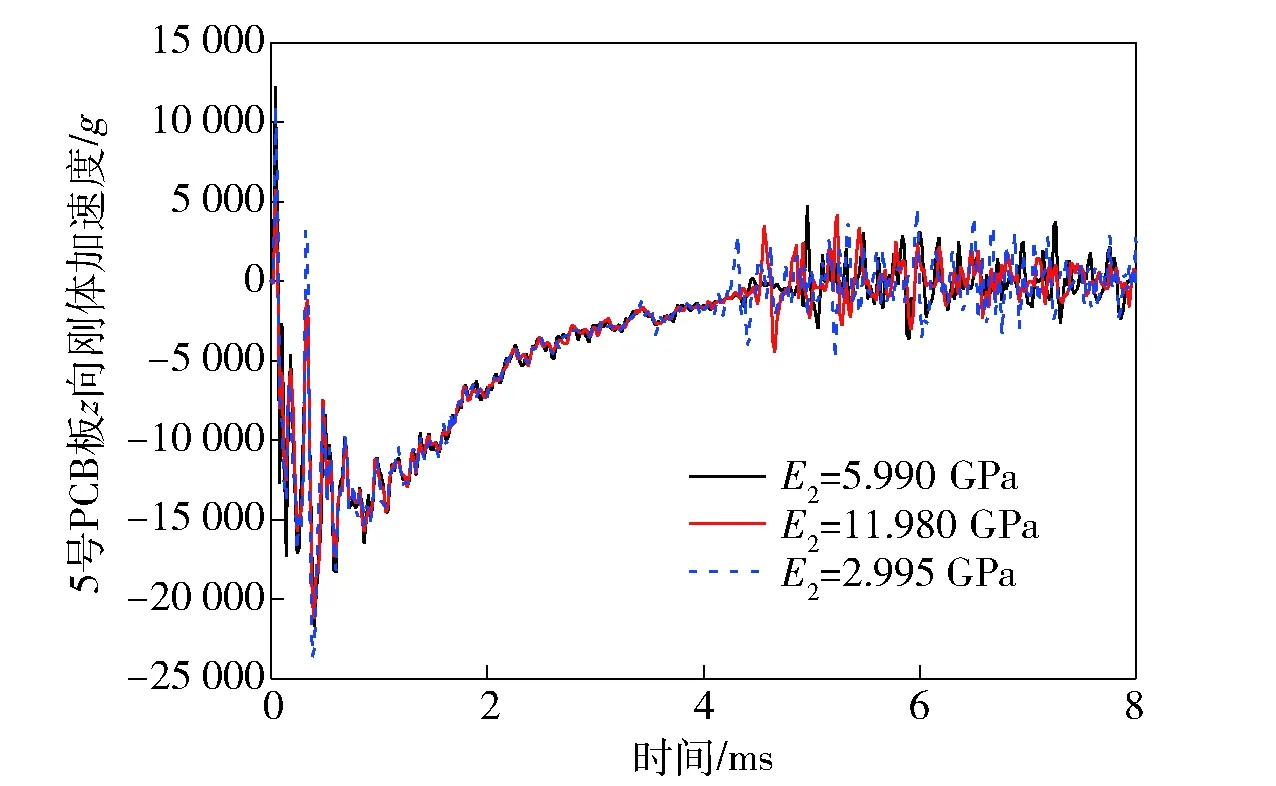
图20 5号PCB板的z轴加速度Fig.20 Acceleration of PCB 5’s z-axis

图21 1号负载中心单元的等效应力Fig.21 v-m stress of payload 1’s center element

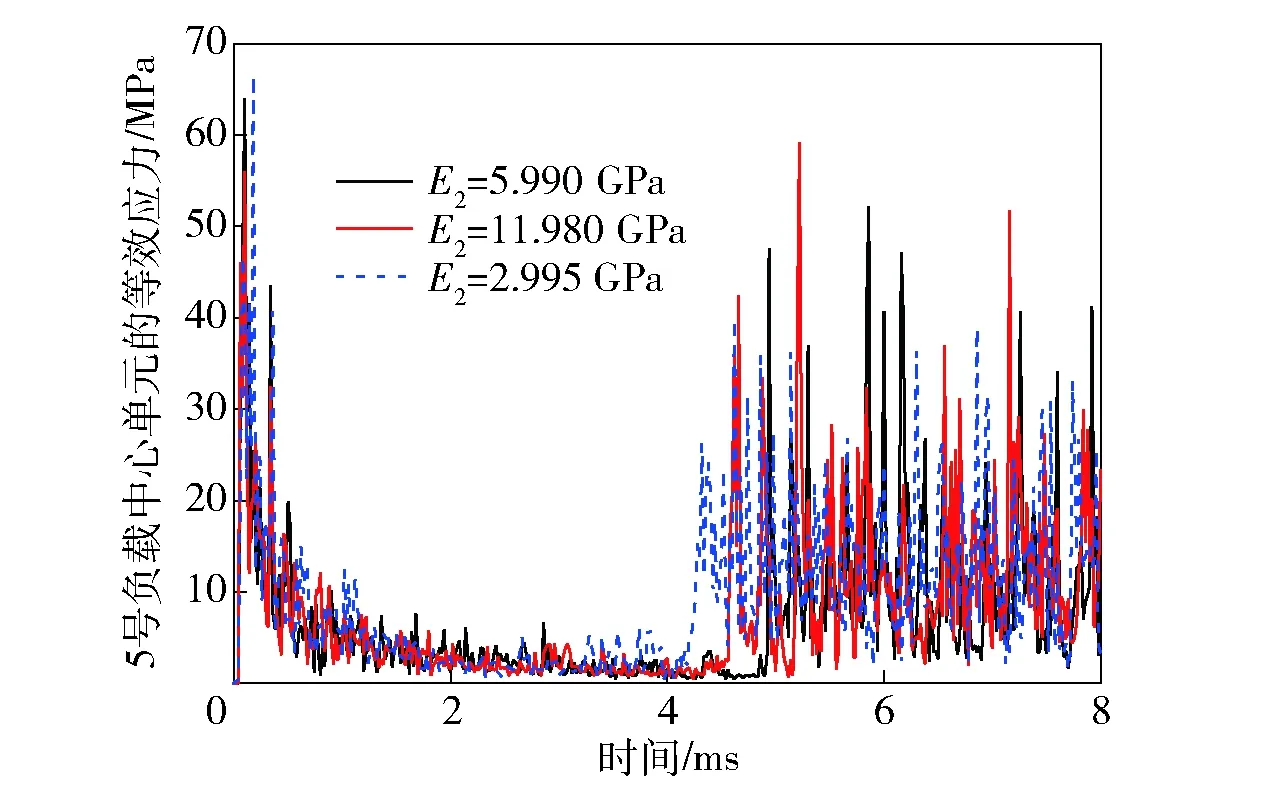
图22 5号负载中心单元的等效应力Fig.22 v-m stress of payload 5’s center element

3.3.4 参数θ2的影响

图23～图26别给出了1号和5号PCB板的轴向刚体加速度及中心单元等效应力随参数θ2变化规律。从图23和图24中可以看出，加速度曲线仅在后期的震荡阶段随着θ2的减小而有所衰减，在侵彻前期没有明显变化。图25和图26的等效应力曲线在整个侵彻阶段都随着θ2的减小而有明显的衰减。

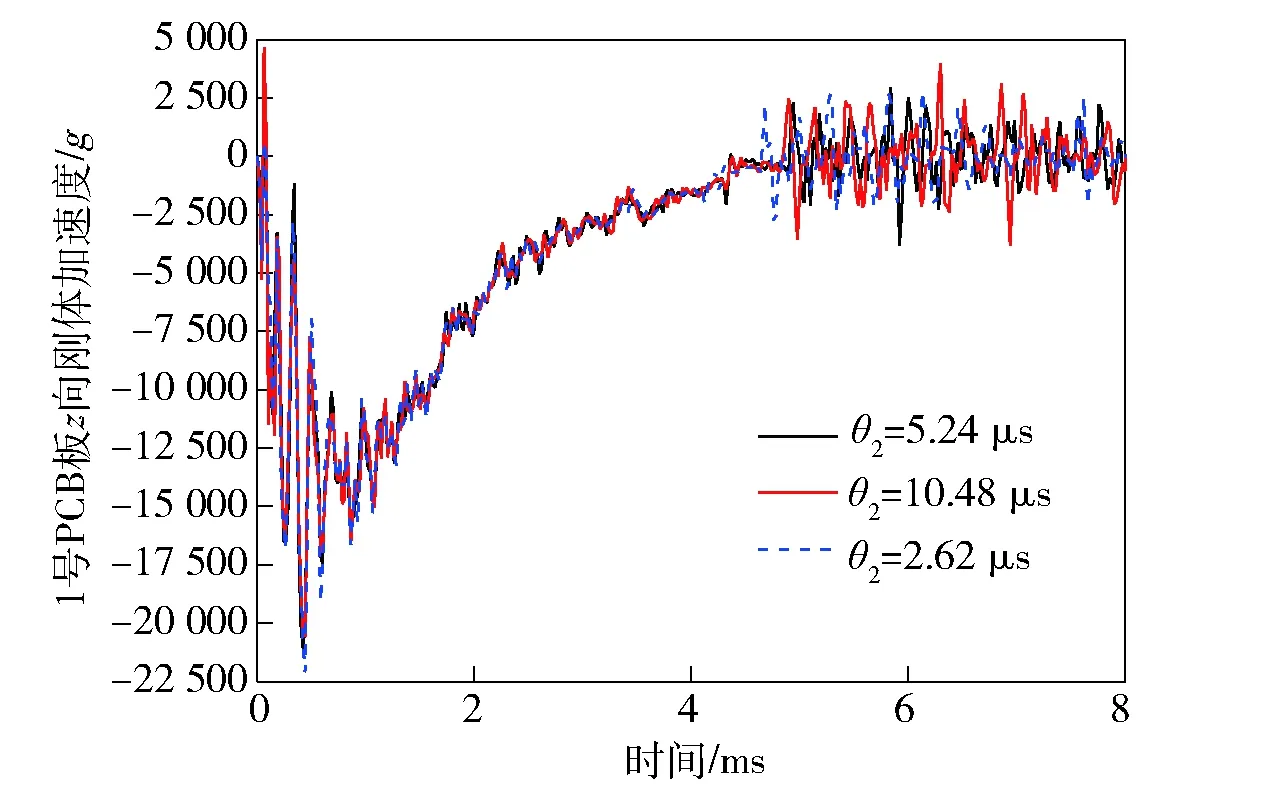
图23 1号PCB板的z向刚体加速度Fig.23 Acceleration of PCB 1’s z-axis rigid body

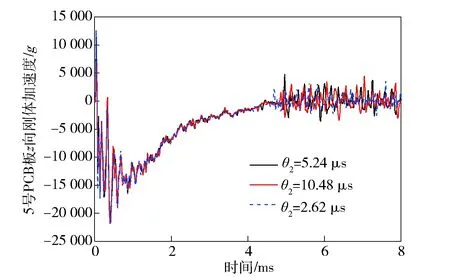
图24 5号PCB板的z向刚体加速度Fig.24 Acceleration of PCB 5’s z-axis rigid body

图25 1号负载中心单元的等效应力Fig.25 v-m stress of payload 1’s center element

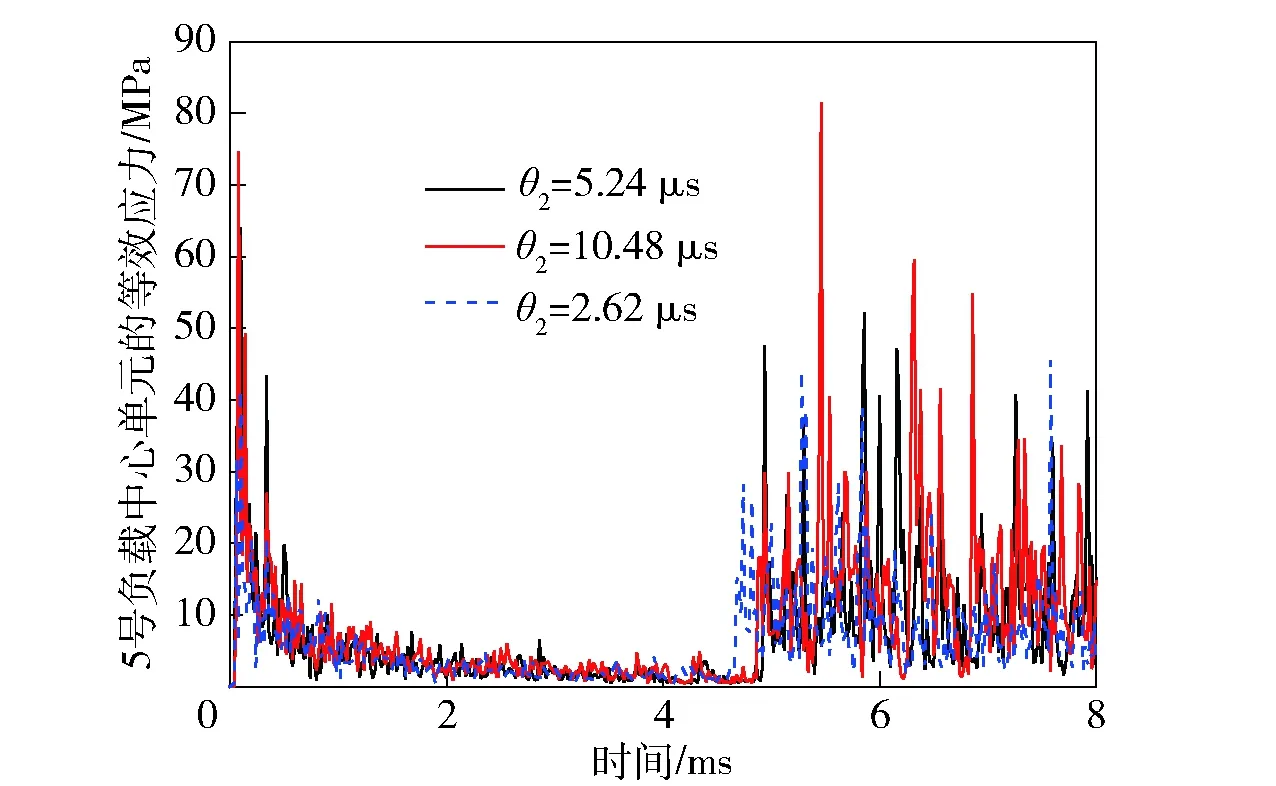
图26 5号负载中心单元的等效应力Fig.26 v-m stress of payload 5’s center element

3.3.5 密度ρ的影响

图27～图30为1号和5号PCB板的轴向刚体加速度及中心单元等效应力随参数ρ的变化规律。可以看出，图27和图28的加速度曲线在侵彻前期的幅值随着密度的减小而升高，在后期震荡阶段幅值却随着密度的减小而降低；图29和图30的应力曲线可以看出，密度最大算例的最大应力值最小，密度中间者的最大应力值反而最大，二者之间并不是单调关系，具体原因有待下一步分析。

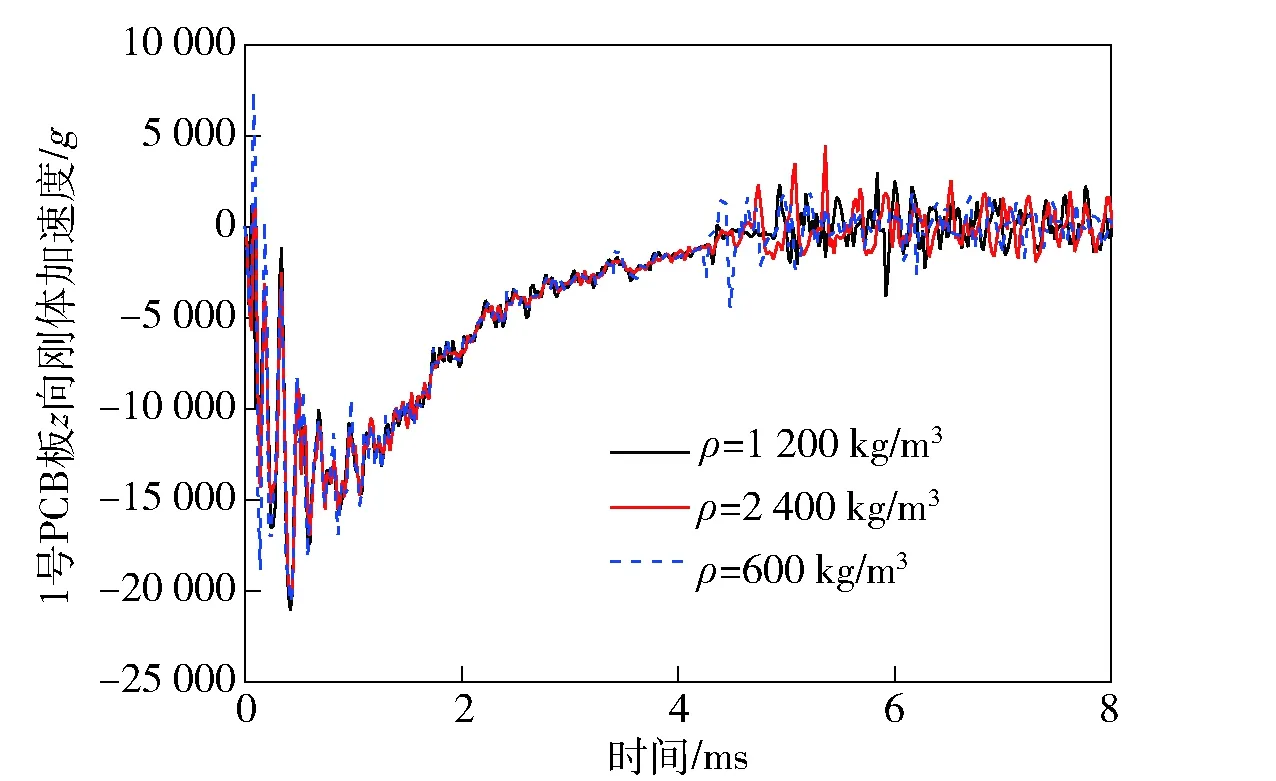
图27 1号PCB板的z向刚体加速度Fig.27 Acceleration of PCB 1’s z-axis rigid body

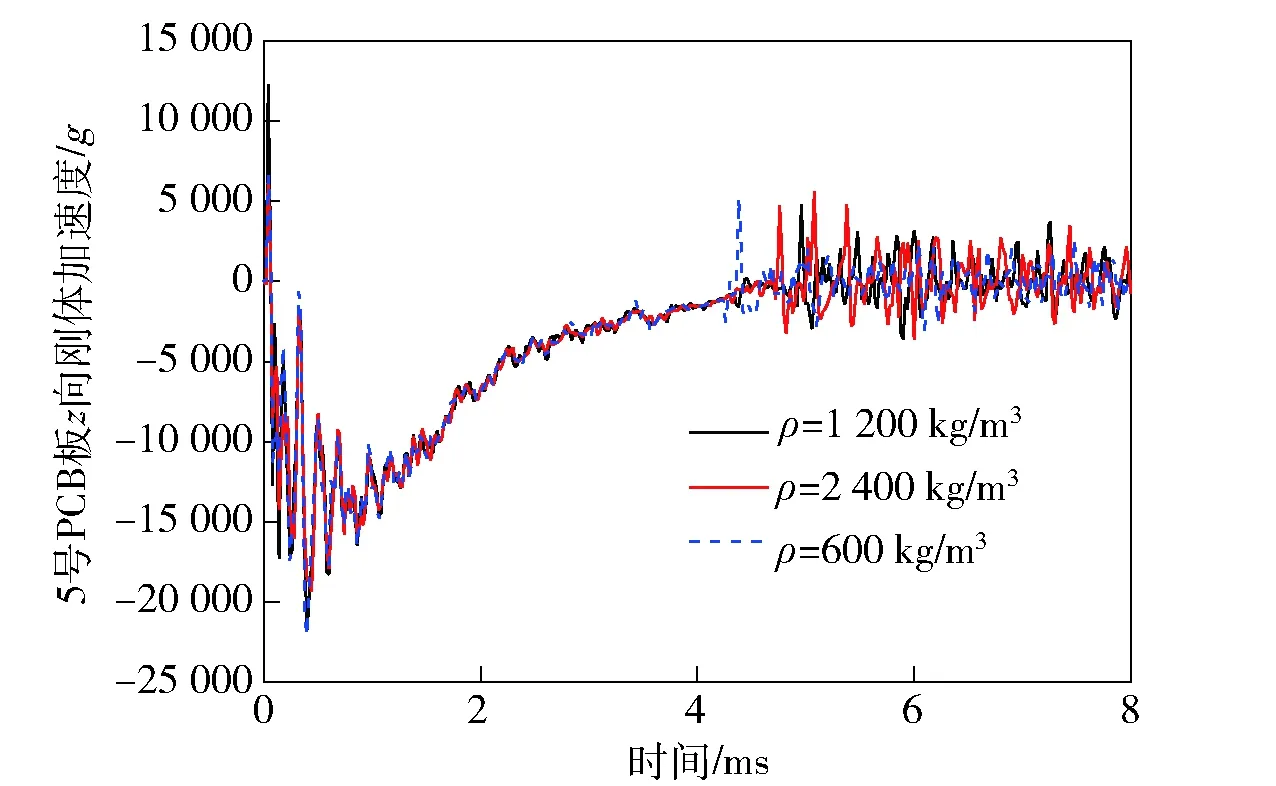
图28 5号PCB板的z向刚体加速度Fig.28 Acceleration of PCB 5’s z-axis rigid body

图29 1号负载中心单元的等效应力Fig.29 v-m stress of payload 1’s center element

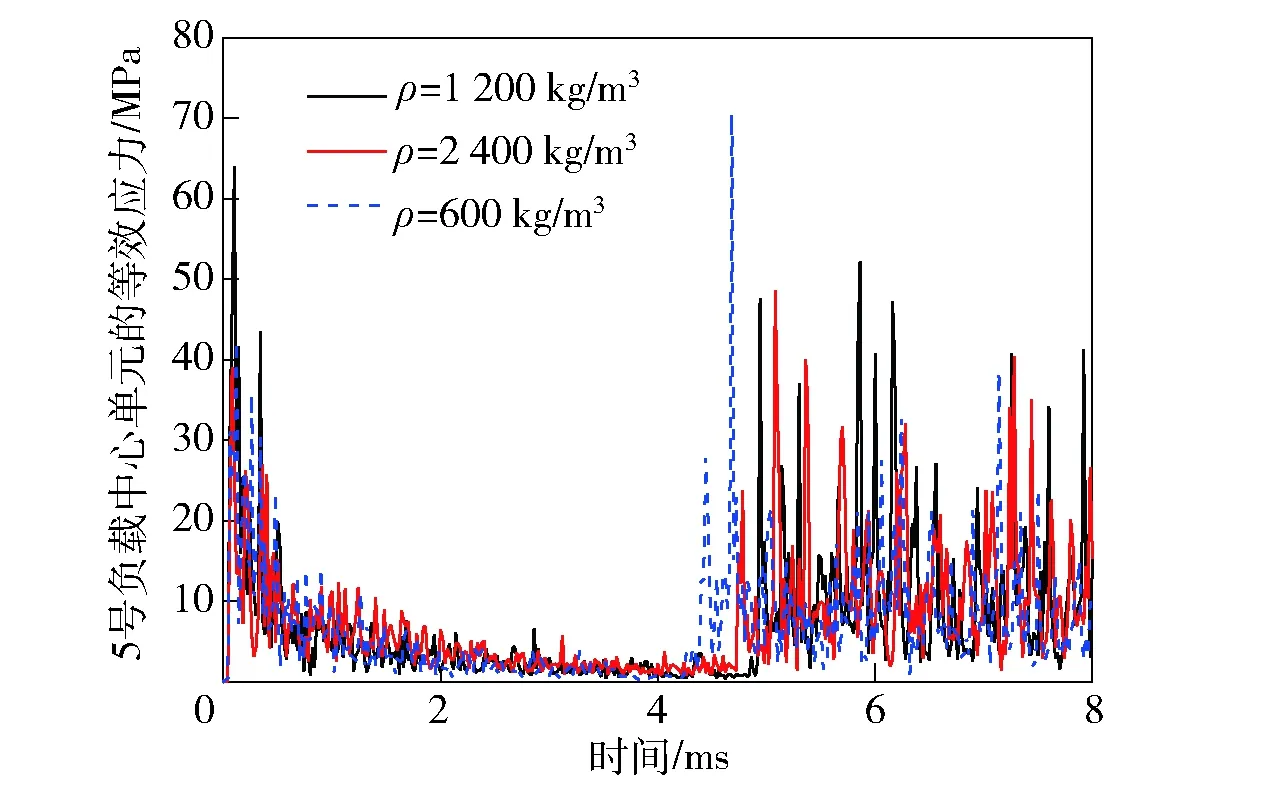
图30 5号负载中心单元的等效应力Fig.30 v-m stress of payload 5’s center element

3.3.6 整体分析

从上述分析可以看出，在降低E0、E1和θ2时，对于PCB的刚体加速度和负载单元的等效应力来说有较为明显的双重衰减削弱作用；而降低ρ和E2对于结构的动力学响应的影响却不是那么简单。

根据应力波理论[11, 16]，冲击波在ZWT非线性黏弹性材料中传递的波速为

(6)

波阵面上应力按照指数规律衰减：

σ=σ0exp (-αax)，

(7)

式中：σ0是冲击边界上的初始应力；αa为衰减因数，

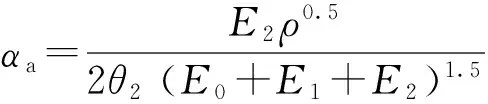
(8)

显而易见，在灌封材料的波速较低，且衰减因数较大的情况下，对于冲击的缓冲效果最佳。由(6)式和(8)式可得，当降低E0、E1和θ2时，既能降低波速，又能增大衰减因数，明显提高材料的缓冲吸能效率。当降低ρ和E2时，降低波速的同时也降低衰减因数；增加ρ和E2的大小则会增大波速也增大衰减因数，二者一增一减相互作用弱化了其对于材料衰减吸能特性的影响，这与前文仿真数据对比结论相吻合。

4 结论

本文通过算例验证UMAT子程序描述ZWT本构模型的可行性，并将其应用于引信结构的动态响应仿真，分析了此类引信结构对于电子器件动态响应的影响。在此基础上，分别改变环氧树脂的ZWT非线性黏弹性模型参数，如E0、E1、E2、θ2、ρ，进行多种工况的计算，对比研究材料参数对引信灌封材料缓冲效果的影响。得出结论如下：

1)通过每个PCB板和板上负载的动态响应分析，1号PCB的加速度最小，但负载应力值较大，5号PCB的加速度和负载应力值都较大。整体来说前端和末端的负载环境最为恶劣，因此在实际工程中，应避免将PCB板放置的过于靠后。

2)如果工程需要更侧重于降低引信内部组件的加速度峰值，选用E0、E1、θ2较小，ρ较大的灌封材料更有效；如果工程需要更侧重于降低PCB板上负载所承受的应力值，选用E0、E1、θ2和ρ较小的灌封材料更有效；参数E2对衰减的影响很微弱，建议不作考虑。

本文目前只针对一种引信结构计算分析了材料参数对电子器件动态响应的作用，尚存在一定的局限性。下一步研究重点考虑引信结构尺寸变化对于动态响应的影响，为引信结构设计提供更为完善充分的理论依据。

References)

[1] 赵小龙, 马铁华, 范锦彪. 弹载常用芯片在高g值冲击下的失效分析[J]. 仪器仪表学报, 2013, 34(10):2358-2364. ZHAO Xiao-long, MA Tie-hua, FAN Jin-biao. Failure analysis of common missile-borne chip in highgshock[J]. Chinese Journal of Scientific Instrument, 2013, 34(10):2358-2364.(in Chinese)

[2] 鲍爱达, 陈员娥, 李长龙, 等. 弹载加速度记录仪在冲击环境下的失效研究[J]. 振动与冲击, 2013, 32(13):182-186. BAO Ai-da, CHEN Yuan-e, LI Chang-long, et al. Failure study on a missile accelerometer recorder under shock environment[J]. Journal of Vibration and Shock, 2013, 32(13):182-186. (in Chinese)

[3] 秦丽, 陈员娥, 李峰. 弹载存储设备在侵彻下的失效分析[J]. 弹箭与制导学报, 2014, 34(4): 158-161. QIN Li, CHEN Yuan-e, LI Feng. Failure analysis of missile-borne storage device under penetration[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2014, 34(4): 158-161.(in Chinese)

[4] 马其琪, 徐晓辉, 孔雁凯, 等. 弹载记录器的抗高过载分析及设计[J]. 弹箭与制导学报, 2015, 35(1):15-18. MA Qi-qi, XU Xiao-hui, KONG Yan-kai, et al. Anti-high overload analyses and design of missile-borne recorder[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2015, 35(1):15-18.(in Chinese)

[5] 尚雅玲, 彭艳垒, 梁捷. 引信抗大过载技术研究及方案设计[J]. 舰船电子工程, 2012, 32(6): 121-124. SHANG Ya-ling, PENG Yan-lei, LIANG Jie. Research of fuze resisting highg-load technology and scheme design[J]. Ship Electronic Engineering, 2012, 32(6): 121-124. (in Chinese)

[6] Chakka V, Trabia M B, O’Toole B, et al. Modeling and reduction of shocks on electronic components within a projectile[J]. International Journal of Impact Engineering, 2008, 35(11): 1326-1338.

[7] 尹威华, 杨国来, 葛建立, 等. 弹载测试电路模块缓冲防护结构设计及优化[J]. 火炮发射与控制学报, 2016, 37(3):56-60. YIN Wei-hua, YANG Guo-lai, GE Jian-li, et al. Design and optimization of cushioning and protective structure for a circuit module of projectile-borne testing equipment[J]. Journal of Gun Launch & Control, 2016, 37(3):56-60.(in Chinese)

[8] Berman M S. Electronic components for high-g hardened packaging, ARL-TR-3705[R]. Harford, MD, US: Army Research Lab Aberdeen Proving Ground, 2006.

[9] 卢剑平, 徐鹏, 王燕. 高过载环境下轻质电路缓冲保护方法[J]. 探测与控制学报, 2015, 37(6): 99-102. LU Jian-ping, XU Peng, WANG Yan. High overload buffer protection of light circuit module[J]. Journal of Detection & Control, 2015, 37(6): 99-102. (in Chinese)

[10] 焦敏, 陈小伟, 阮朝阳, 等. 灌封材料对弹载电子器件的防护仿真研究[J]. 兵工学报, 2014, 35(增刊2):51-56. JIAO Min, CHEN Xiao-wei, RUAN Zhao-yang, et al. Numerical analysis on potting protection of electronic components in projectile[J]. Acta Armamentarii, 2014, 35(S2):51-56. (in Chinese)

[11] 王礼立. 应力波基础[M]. 北京:国防工业出版社, 2005:166-169. WANG Li-li. Foundation of stress waves[M]. Beijing:National Defense Industry Press, 2005:166-169. (in Chinese)

[12] 冯震宙, 王新军, 王富生, 等. 朱- 王- 唐非线性黏弹性本构模型在有限元分析中的实现及其应用[J]. 材料科学与工程学报, 2007, 25(2): 269-272. FENG Zhen-zhou, WANG Xin-jun, WANG Fu-sheng, et al. Implementation and its application in finite element analysis of constitutive model for ZWT nonlinear viscoelastic material[J]. Journal of Material Science & Engineering, 2007, 25(2): 269-272. (in Chinese)

[13] Uzair A, Wang J, Xu Y J, et al. High-speed bird impact analysis of aircraft windshield by using a nonlinear viscoelastic model[J]. Applied Mechanics & Materials, 2013, 290:85-90.

[14] 王礼立, 朱锡雄, 施绍裘, 等. 鸟撞高速飞机风挡若干问题的冲击动力学研究[J]. 航空学报, 1991, 12(2): 27-33. WANG Li-li, ZHU Xi-xiong, SHI Shao-qiu, et al. An impact dynamics investigation on some problems in bird strike on windshields of high speed aircrafts[J]. Acta Aeronautica et Astronautica Sinica, 1991, 12(2): 27-33. (in Chinese)

[15] 周光泉, 刘孝敏. 黏弹性理论[M]. 合肥:中国科学技术大学出版社, 1996:85-91. ZHOU Guang-quan, LIU Xiao-min. Viscoelastic theory[M]. Hefei: University of Science and Technology of China Press, 1996:85-91. (in Chinese)

[16] 王礼立. 冲击载荷下高聚物动态本构关系对黏弹性波传播特性的影响[J]. 宁波大学学报: 理工版, 1995, 18(3): 30-57. WANG Li-li. The influence of dynamic constitutive relations of polymers at impact loading on the viscoelastic wave propagation character[J]. Journal of Ningbo University: Natural Science & Engineering Edition, 1995, 18(3): 30-57. (in Chinese)

[17] 王礼立. 冲击动力学进展[M]. 合肥:中国科学技术大学出版社, 1992:96-99. WANG Li-li. Advances in impact dynamics[M]. Hefei: University of Science and Technology of China Press, 1992:96-99. (in Chinese)

Dynamic Analysis of Projectile-borne Electronic Devices under Impact Loading

XU Xiao1, GAO Shi-qiao1, NIU Shao-hua1, SHEN Li2, LIU Hai-peng1, OU Zhuo-cheng1

(1.School of Mechatronic Engineering, Beijing Institute of Technology, Beijing 100081, China; 2.Institute of Navigation and Control Technology, China North Industries Group Corporation, Beijing 100089, China)

The dynamic responses of projectile-borne electronic devices which are protected by encapsulating material under impact loading are studied through numerical simulation. A LS-DYNA user defined material subroutine is established according to the ZWT nonlinear viscoelastic model which is used for simulating the dynamic response of the encapsulating material in the projectile. The simulations of projectile penetration were performed by adjusting the controllable parameters of ZWT model, such as nonlinear elasticity modulus, low strain rate Maxwell elastic constant, high strain rate Maxwell elastic constant, high strain rate Maxwell relaxation time and material density. Thus the dynamic responses of projectile-borne electronic devices could be obtained from the numerical results. The research results show that the shock absorption and protection effects of the encapsulating materials are better when the values of nonlinear elasticity modulus, low strain rate Maxwell elastic constant, high strain rate Maxwell relaxation time and material density are decreased.

ordnance science and technology; nonlinear viscoelastic model; electronic device; numerical simulation

2016-10-26

国家自然科学基金项目(11370245)

徐萧(1990—)，女，博士研究生。E-mail：xuxiao_1990@126.com

牛少华(1975—)，男，讲师，硕士生导师。E-mail：shh@bit.edu.cn

TJ430.2

A

1000-1093(2017)07-1289-12

10.3969/j.issn.1000-1093.2017.07.006