油气弹簧主活塞斯特封泄漏流量计算与仿真研究

桂鹏， 毛明， 陈轶杰， 郭建娟， 高晓东， 宁丹

(中国北方车辆研究所 底盘部件技术部, 北京 100072)

油气弹簧主活塞斯特封泄漏流量计算与仿真研究

桂鹏， 毛明， 陈轶杰， 郭建娟， 高晓东， 宁丹

(中国北方车辆研究所 底盘部件技术部, 北京 100072)

针对油气弹簧主活塞斯特封宽温域条件下的工作稳定性问题，基于材料力学及流体动力学分析与计算，建立了流体动密封数学模型，推导出了斯特封泄漏流量的理论计算公式；运用有限元模型获取密封间隙处的油膜压力数据，研究了工作温度、往复运动速度、预压缩率及沟槽尺寸对斯特封泄漏流量的影响规律。结果表明：同等工况下，往复运动速度增加、预压缩率减小、沟槽宽度或深度增大都会增加斯特封的泄漏流量；在材料许用温域范围内，随着工作温度的升高，斯特封的泄漏流量增加。

兵器科学与技术; 斯特封; 泄漏流量; 油气弹簧

0 引言

油气弹簧是用高压惰性气体替代传统的一种弹性元件，它具有典型的非线性、变刚度特性，能够较好地满足车辆行驶平稳性的要求，对于提高车辆行驶速度，改善车辆的机动性有明显优势，因此在高机动车辆方面有强烈需求。但由于油气弹簧结构的复杂性及工作环境的恶劣性，其高压组合密封特别是宽温域下的高压组合密封可靠性，是一个技术难点。斯特封作为油气弹簧的主要密封形式，其密封性能对油气弹簧的宽温域使用性能起决定性作用。

斯特封一般由O形密封圈和改良的聚四氟乙烯(PTFE)基体组成，具有很强的泵油功能[1]，从而改善润滑条件，防止泄漏。泄漏流量是衡量密封件密封性能的重要指标。密封件的泄漏流量关系着整个液压系统的可靠性与安全性，泄漏流量过大会导致液压系统的失效。密封件的泄漏流量由油膜压力、温度、油膜厚度3个参数决定。而这3个参数取决于密封件的结构尺寸、材料属性、运转工况与系统压力、温度、介质等影响因素[2]。因此，系统地研究这些影响因素对密封件密封性能的影响规律，对密封件的设计、选型与使用具有重要意义。

国内外学者对密封件的研究主要集中在简单的单一密封圈，如矩形圈[3-5]、O形圈[6-9]等，对斯特封的研究较少。对于斯特封研究[10]主要采用有限元进行仿真，基于不同工况下的应力分布对斯特封的密封性能进行分析，没有给出泄漏流量的解析式。本文基于材料力学与流体动力学，推导了斯特封泄漏流量的理论公式，重点研究了工作温度、往复运动速度、预压缩率和沟槽尺寸对斯特封泄漏流量的影响规律。

1 流体动密封模型的建立

斯特封安装在主活塞后的示意图如图1所示。图1中Dp为主活塞外径，dc为缸筒内径，T为安装槽深度，p(y)为油膜压力沿y方向的分布。斯特封安装前后的变形示意图见图2和图3. 工作状态下，主活塞在缸筒内作往复运动，斯特封安装在主活塞的安装槽内。不妨将往复运动中油液压力升高的行程定义为压缩行程，将油液压力降低的行程定义为拉伸行程。

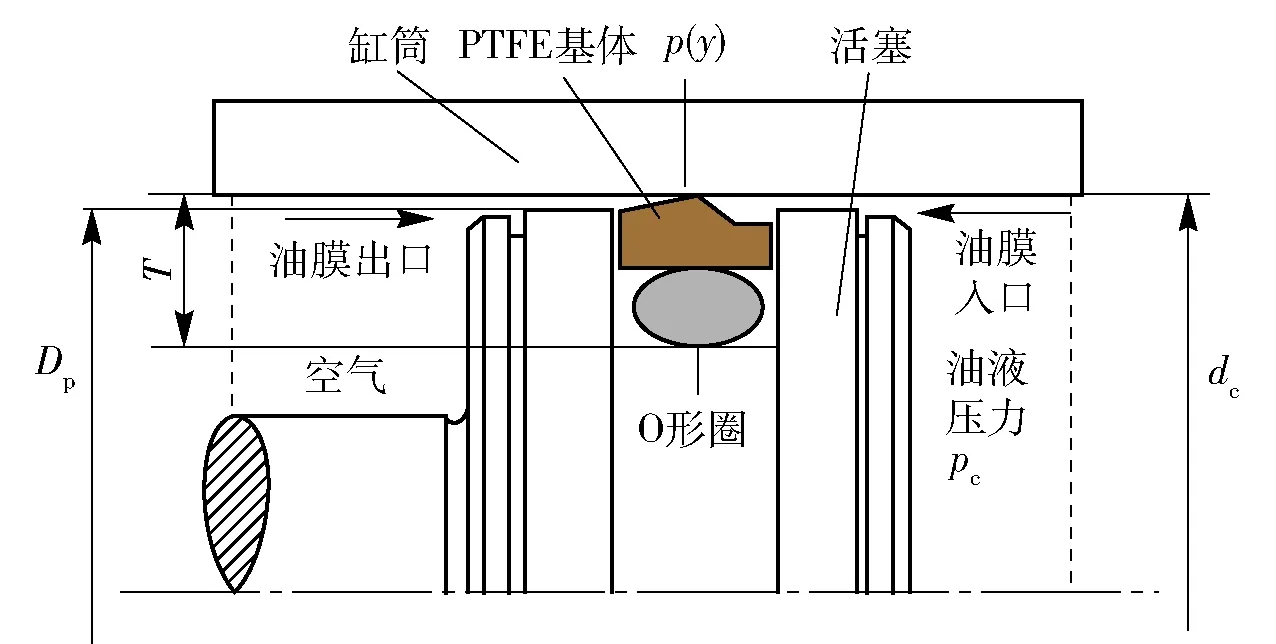
图1 斯特封安装示意图Fig.1 Schematic diagram of Stepseal after assembling

图2 斯特封安装前有限元仿真示意图Fig.2 Schematic diagram of simulated Stepseal before assembling

图3 斯特封安装后有限元仿真示意图Fig.3 Schematic diagram of simulated Stepseal after assembling

工作状态下斯特封的变形由两部分组成，分别为安装后的预压缩变形与油液压力作用下的变形。在分析斯特封变形的过程中，将PTFE基体与O形圈看作一个整体。自由状态下，密封圈外径尺寸为Ds，内径尺寸为ds.

1.1 密封圈安装预压缩变形分析

弹性体的往复动密封需要满足静密封条件[1]。因此，自由状态下斯特封内径ds小于安装槽槽底直径dg，斯特封外径Ds大于缸筒内径dc. 假设密封圈的安装及变形具有对称性，其在内外圈的变形均为δ0，如图4所示。δ0的表达式为

(1)

图4 斯特封安装变形示意图Fig.4 Schematic diagram of deformed Stepseals

为了方便分析，以油膜入口处靠近缸筒侧为原点，以油气弹簧的轴向方向为y轴，以油膜厚度方向为z轴，建立如图5所示的直角坐标系。

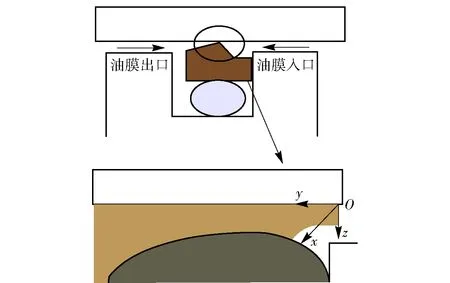
图5 坐标系建立示意图Fig.5 Schematic diagram of coordinate system

斯特封安装在密封槽中后径向受压产生变形，假定在径向方向产生的预紧压力在y方向上均匀分布，并用p0表示。

1.2 密封圈受油液压力作用时径向变形分析

在主活塞往复运动的过程中，密封油液的压力与间隙处的油膜压力共同作用，使密封圈进一步发生径向变形。与其他区域的尺寸相比，油膜厚度尺寸非常小。按密封理论中密封的接触压力分布与油膜中的压力分布相同的基本假设[1]，可以假设在密封接触部分的流体区域内，流体的压力和黏度沿油膜厚度方向不变。油膜压力虽然在厚度方向上不发生变化，但在轴向方向上的分布是随坐标值的变化而变化的，因此将油膜压力沿y方向分布表示为函数p(y)。

采用微体积的应变能函数法对密封圈的径向变形进行分析，取密封圈任一位置处的微元分析油液压力作用后的密封圈变形。在安装预紧力和油液压力的共同作用下，微元体由图6(a)变形为图6(b)。由于橡胶材料的不可压缩性，在自由状态下及油液压力作用后橡胶密封体的体积不变，可得

(2)

整理(2)式并消去2阶及3阶无穷小量得

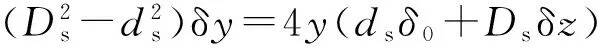
(3)

式中：δy、δz分别为微元体在y方向、z方向上相对于自由状态的变形量。

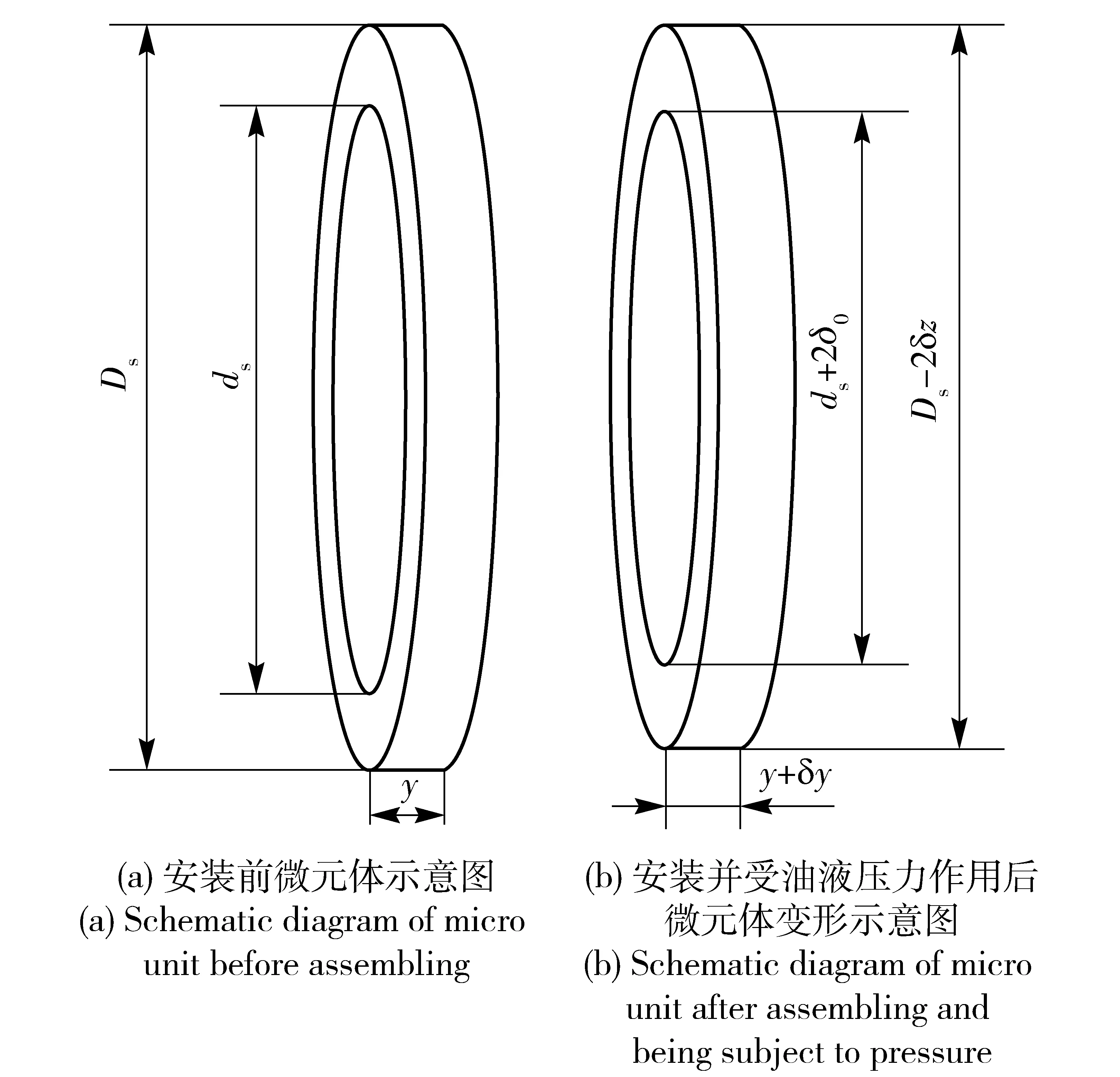
图6 受安装预紧力和油液压力作用下径向变形示意图Fig.6 Radial deformation of micro-unit subjected to oil pressure

假设微元体在y方向、z方向上的变形均匀，变形与应变之间的关系为线性，则δy、δz与y方向、z方向上的应变εy、εz之间的关系分别为δy=yεy、δz=(Ds-ds)/2εz，将这两个关系式代入(3)式，可得到y方向和z方向应变之间的关系为

(4)

如图6所示，在有油液压力作用时，密封体在y方向上作用有油液压力pc，而密封体在z方向上同时受到油膜压力p和预紧压力p0的作用。在pc、p与p0的共同作用下，图6中微元体由图6(a)变形到图6(b)，则从自由状态下到安装后有油液压力作用时，各作用力在微元体上所做的功为

(5)

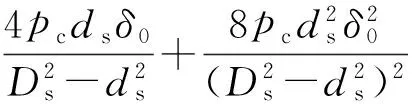
(6)

由于密封圈在z方向上的伸长率λz=1+εz，则由密封圈变形分析的应变能函数推导出的橡胶材料应力与应变关系式为

(7)

除此之外，国内外学者基于应变能密度函数，提出了很多描述橡胶材料大变形的应力与应变关系的模型[11]。其中2常数的Mooney-Rivlin模型、5常数的Mooney-Rivlin模型和9常数的Mooney-Rivlin模型在工程中应用广泛。 2常数的Mooney-Rivlin模型中，两个材料常数分别用C10和C01表示，其应力与应变的关系式[12]为

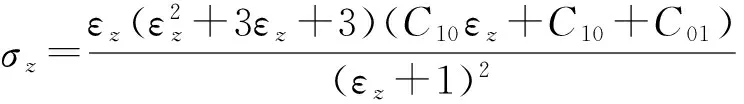
(8)

联立(7)式、(8)式，通过有限元仿真模型获取安装预紧力p0与油膜压力p，由于结构参数Ds、ds、δ0已知，输入两个材料常数C10和C01与油液压力pc，就可求得应变εz值，进而求得密封圈外圈的总变形2δz. 结合图6可知，密封圈安装在活塞杆上并受油液作用时密封圈外径的变形量为sf=|δz|.

本节基于密封圈安装与变形的对称性假设，采用微体积的应变能函数法，建立了动密封条件下密封圈变形量的数学模型，为后续油膜厚度与流动流量的计算奠定基础。

2 变间隙缝隙流动流量计算

2.1 密封间隙处油膜厚度确定

油膜厚度的表达式[3-5, 13]为

h=sp+ss+sf,

(9)

式中：sp为活塞粗糙度引起的平均油膜间隙；ss为密封圈粗糙度引起的平均油膜厚度；sf为安装预紧力、油膜压力、轴向油液压力共同作用下引起的密封圈外径的变形量。

2.2 间隙流动流体速度与流量计算

充满油液的配合间隙广泛存在于机械设备中，主活塞与缸筒之间的环形间隙是一种典型的变间隙缝隙流动。变间隙缝隙液体流动速度vy的分布规律表达式[1]为

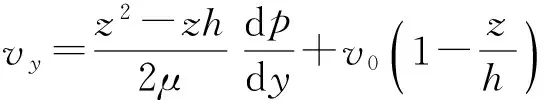
(10)

式中：μ为流体的动力黏度(Pa·s)；v0为主活塞往复运动的速度(m/s)。

变间隙缝隙流动中流体的流动方向均沿y轴，在对变间隙缝隙流动的流量qv进行计算时，选取平行于z轴的控制面，此控制面与速度方向相互垂直称为过流断面,如图7所示。单位时间内流过某一控制面的流体体积称为该控制面的流量，所以密封间隙处的流量有

qv=∫AvydA=

(11)

计算上述积分可得

(12)

式中：δi为油膜入口处密封圈的径向变形量；wc为接触宽度，wc=(1+εy)w；m=(Dp+h)/h；C为积分常数。

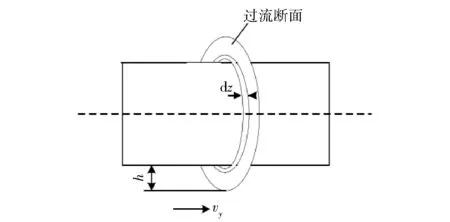
图7 过流断面的选取Fig.7 Schematic diagram of cross section of passage

弹性体密封间隙处的边界条件如下：

(13)

式中：ho为出口处油膜厚度；hi为入口处油膜厚度。

将边界条件代入(12)式，可求得变间隙缝隙流动的流量表达式为

qv=

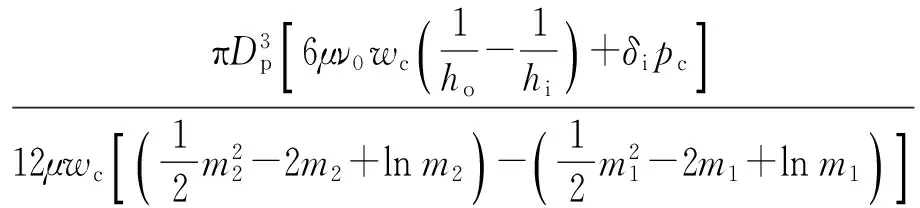
(14)

式中：m1=(Dp+hi)/hi；m2=(Dp+ho)/ho.

运用有限元仿真模型，获取安装预紧力p0、油膜压力p及接触宽度wc，基于前文所建立的流体动密封模型，求得密封圈安装在活塞杆上并受油液作用时的密封圈外径的变形量sf，进而求得油膜入口与出口处的油膜厚度hi、ho与油膜入口处密封圈的径向变形量δi. 而结构参数Dp、油液动力黏度μ、油液压力pc、往复运动速度v0皆为已知，按(14)式就可以求出变间隙缝隙流动的流量qv.

3 各因素影响规律分析

Abaqus是一款功能强大的有限元分析软件，在橡胶材料的仿真等非线性问题的求解上具有显著优势。在Abaqus中建立缸筒、活塞与斯特封的二维轴对称有限元模型。定义PTFE基体的弹性模量为572.3 MPa，泊松比为0.4，接触面之间的摩擦系数设为0.1. 橡胶材料与PTFE基体的网格划分均为CAX4H(四节点双线性轴对称四边形杂交单元)。

采用有限元仿真获取斯特封密封间隙处的油膜压力，结合(14)式，分析工作温度、往复运动速度、预压缩率与沟槽尺寸对斯特封泄漏流量的影响规律。将单次压缩行程带出的流体流量定义为压缩行程流量，将单次复原行程带回的流体流量定义为复原行程流量，将单次循环(一次压缩行程与之后相邻的一次复原行程的组合)密封件带出的净流体流量定义为单次循环泄漏流量。在(14)式中，压缩行程的主活塞速度v0>0与油液介质压力pc同向，则压缩行程流量为正；复原行程的主活塞速度v0<0与油液介质压力pc反向，则复原行程流量为负。

3.1 工作温度影响规律分析

工作温度对斯特封泄漏流量的影响主要体现在三方面：一方面，温度变化会导致密封件的尺寸变化；另一方面，材料属性会随温度的变化而变化；另外，温度变化会显著影响油液介质的黏度。随着温度的升高，密封组件会产生热膨胀导致尺寸增大，从而使油膜压力升高，影响密封间隙处的油膜厚度。除此之外，温度升高会使油液黏度降低。

采用有限元模型分别对-40 ℃、20 ℃和130 ℃斯特封工作时的油膜压力进行仿真分析，研究工作温度对其泄漏流量的影响规律。-40 ℃和130 ℃分别为军用车辆试验过程中悬挂监测的极限温度。假定斯特封的几何尺寸随温度呈线性变化，改良的PTFE线性热膨胀系数定义为0.000 13，丁腈橡胶O形圈的线性热膨胀系数定义为0.000 149，缸筒及活塞的尺寸变化忽略不计。在20 ℃与130 ℃条件下，采用2参数的Mooney-Rivlin模型来描述O形圈的力学特性，并取材料参数C10=1.87，C01=0.47[14]。经过差示扫描量热(DSC)测试，丁腈橡胶的玻璃化温度约为-32 ℃，见图8. 因此在低温(-40 ℃)条件下，丁腈橡胶已经玻璃化，导致其弹性降低。经过试验测量，此时其应力与应变间的关系可以采用弹性模量为405.29 MPa，泊松比为0.4来描述。

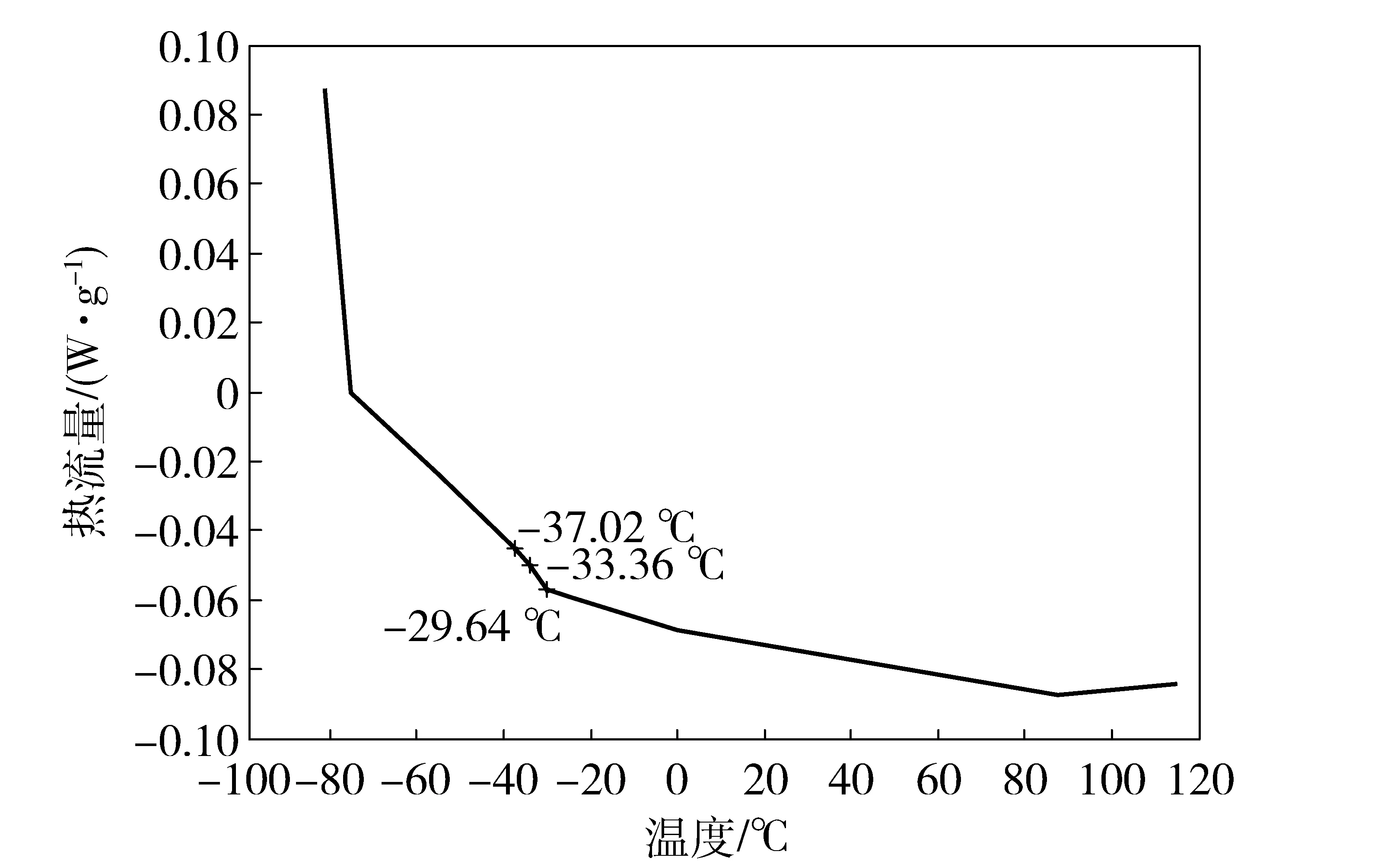
图8 丁腈橡胶O形圈的DSC测试结果Fig.8 DSC test results of NBR O-ring

与此同时，温度变化对油液介质的黏度亦有显著影响。图9为某种油液不同温度下的运动黏度曲线，经过换算，-40 ℃、20 ℃和130 ℃条件下油液的动力黏度分别为1.106 64 Pa·s、0.052 53 Pa·s和0.007 455 03 Pa·s. 活塞的往复运动速度设为2.5 m/s，工作介质的极限压力达到30 MPa.

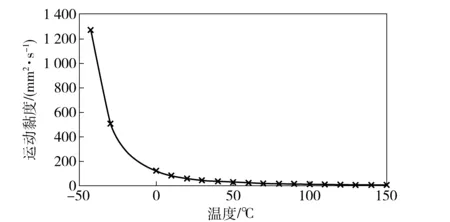
图9 油液的黏度与温度曲线Fig.9 Viscosity-temperature characteristics of hydraulic oil

3种温度条件下斯特封的泄漏流量计算结果见图10. 单次循环泄漏流量的值为正，验证了斯特封良好的泵油功能，即压缩行程能够将复原行程带出的油液全部带回并具有富余的泵回能力。同等工况下，斯特封的泄漏流量随工作介质压力的增加而增加。对比其中的图10(a)与图10(b)可知，当温度从-40 ℃升高到20 ℃时，泄漏流量并没有明显增大。这说明，在-40 ℃条件下，与斯特封几何尺寸及油液黏度的变化相比，O形圈材料属性的变化起主要作用。对比图10(b)与图10(c)可知，当温度从20 ℃升高到130 ℃时，泄漏流量明显增大。这说明，当材料属性不变时，温度升高导致的油液黏度降低是泄漏流量增大的主要原因。

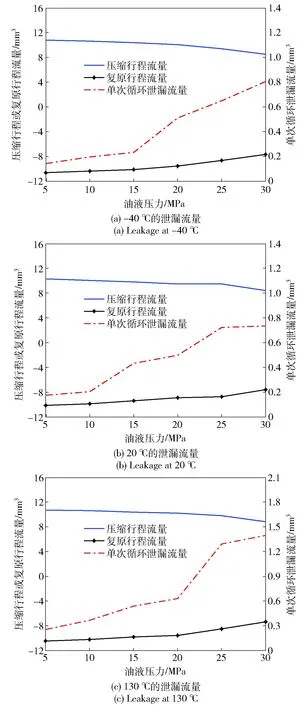
图10 不同温度在不同油液压力下斯特封的泄漏流量Fig.10 Leakages of Stepseals under different sealing pressures at -40 ℃, 20 ℃ and 130 ℃

3.2 往复运动速度影响规律分析

结合(14)式可知，压缩行程的速度v0越大，泄漏流量越大；拉伸行程速度v0越大(不考虑负号)，泄漏流量越大。因此仅从(14)式不能得出主活塞速度v0对单次循环泄漏流量的影响规律。对130 ℃时不同主活塞速度下的斯特封进行仿真，泄漏流量计算结果如图11所示。从图11可以看出，在主活塞的往复运动速度介于0.5 m/s和2.5 m/s之间时，速度越大，斯特封的泄漏流量越大，泄漏流量随介质压力的变化率越大。

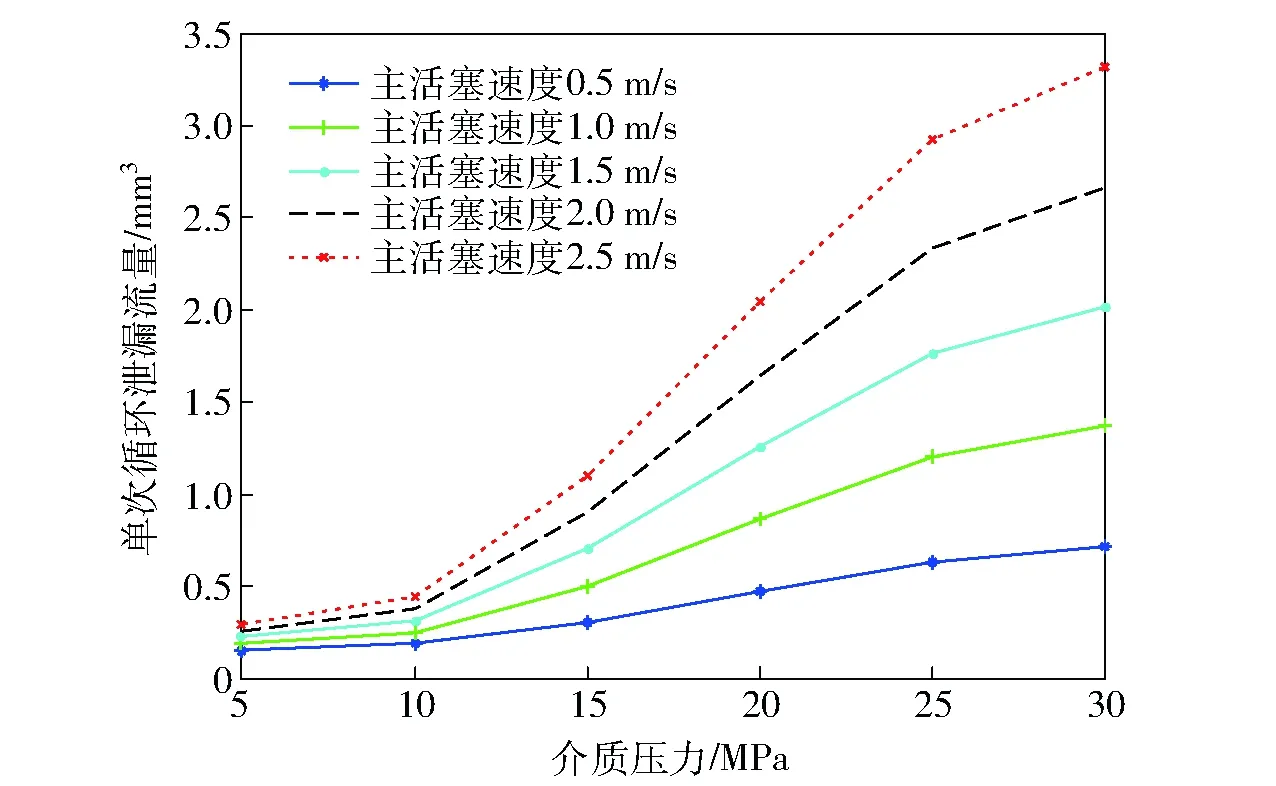
图11 130 ℃时不同主活塞速度对应的斯特封泄漏流量Fig.11 Leakages of Stepseals under different velocities at 130 ℃

3.3 预压缩率影响规律分析

斯特封的预压缩率计算公式为

c=(H-T)/H×100%,

(15)

式中：H为斯特封自由状态下的径向厚度。斯特封的预压缩率越大，油膜压力越大，油膜厚度越小，接触宽度wc随之增大，结合(14)式可知，若不考虑油膜厚度的变化，泄漏流量会随预压缩率增大而减小。

对20 ℃条件下预压缩率为10%～30%的斯特封进行仿真，主活塞往复运动速度均为2.5 m/s，3种工况下的斯特封泄漏流量见图12. 由图12可以看出，同等工况下，斯特封的泄漏流量随预压缩率的增大而减少。当预压缩率小于22%时，泄漏流量随预压缩率增加而快速下降；当预压缩率超过22%时，泄漏流量随预压缩率增加下降的速度有所降低。

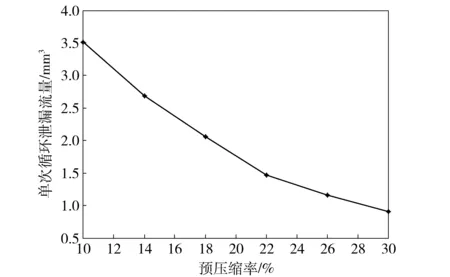
图12 20 ℃时斯特封不同预压缩率对应的泄漏流量Fig.12 Leakages of Stepseals under different compression ratio at 20 ℃

3.4 沟槽尺寸影响规律分析

安装沟槽的尺寸主要有沟槽深度T与沟槽宽度两个尺寸。沟槽深度T对斯特封泄漏流量的影响主要体现在其对预压缩率的影响。即沟槽深度T越大，预压缩率越小，泄漏流量越大，反之亦然。

沟槽宽度的尺寸尽管并未在(14)式中体现，但其会影响接触压力，进而影响斯特封的泄漏流量。对20 ℃条件下沟槽宽度分别为5.5 mm、5.6 mm和5.7 mm的斯特封进行仿真，主活塞往复运动速度均为2.5 m/s，3种沟槽尺寸条件下的斯特封泄漏流量见图13. 从图13可以看出，同等工况下，斯特封的泄漏流量随沟槽宽度的增加而增加。

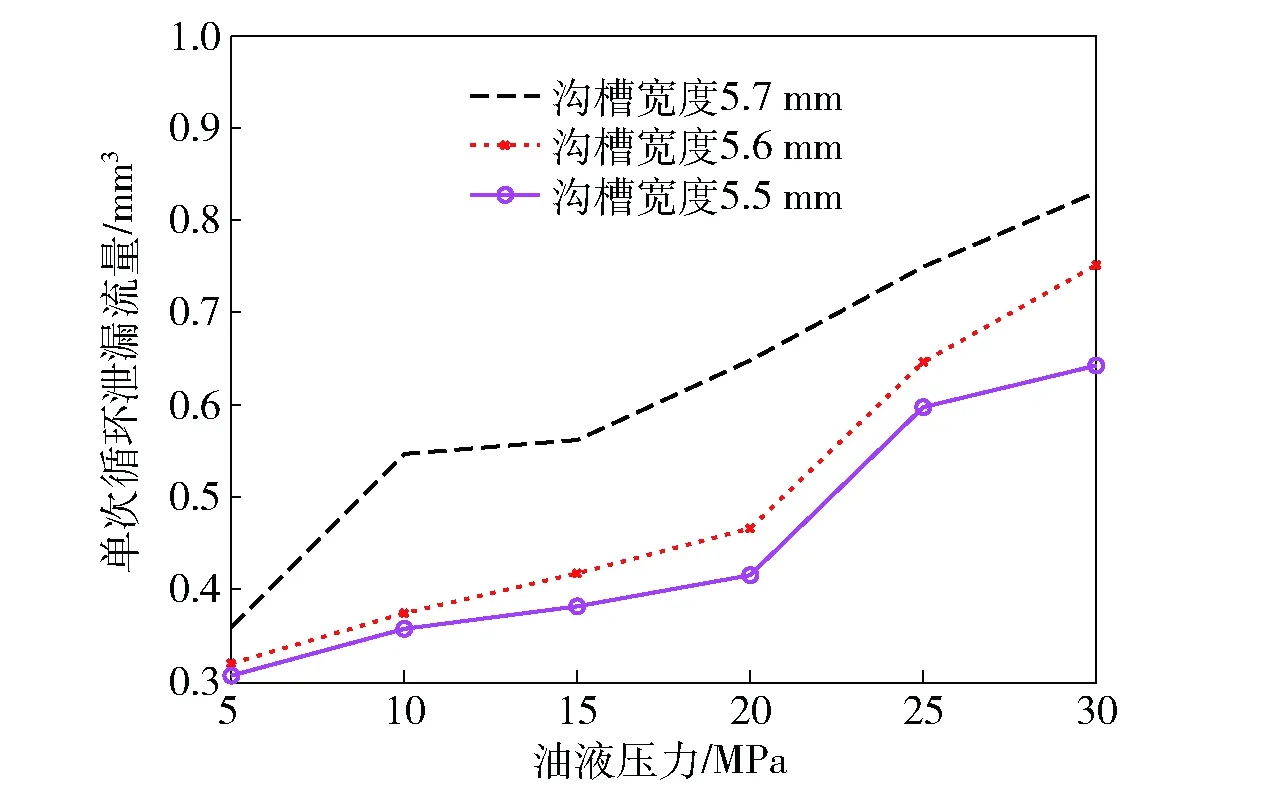
图13 20 ℃时斯特封不同沟槽宽度对应的泄漏流量Fig.13 Leakages of Stepseals under different groove widths at 20 ℃

4 结论

本文基于材料力学与流体动力学，推导了斯特封泄漏流量的理论公式。采用有限元仿真获取油膜压力数据，结合理论公式，研究了工作温度、往复运动速度、预压缩率与沟槽尺寸对斯特封泄漏流量的影响规律。结果验证了斯特封良好的泵油能力，具体结论如下：

1)主活塞的运动速度介于0.5 m/s和2.5 m/s之间时，速度越大，泄漏流量越大，泄漏流量随介质压力的变化率也越大。

2)预压缩率介于10%～30%时，泄漏流量随预压缩率的增大而减少。预压缩率小于22%时，下降速度较快；超过22%时，下降速度变缓。

3)沟槽宽度从5.5 mm增加到5.7 mm，斯特封的泄漏流量随之增大。在沟槽宽度为5.5 mm和5.6 mm时，介质压力小于20 MPa时，泄漏流量随介质压力增加的变化率较小；当介质压力超过20 MPa，泄漏流量随介质压力增加的变化率增大。在沟槽宽度为5.7 mm时，泄漏流量随介质压力的增加呈近似线性增加。

4)温度同时影响斯特封的材料属性、几何尺寸和油液黏度。在-40 ℃条件下，O形圈材料发生玻璃化，是斯特封泄漏量的主要影响因素；在130 ℃条件下，油液黏度的显著降低是斯特封泄漏量的主要影响因素。因此，当温度从20 ℃升高到130 ℃时，斯特封的泄漏流量明显增大。

References)

[1] Müller H K, Nau B S. Fluid sealing technology: principles and applications[M].NY, US: Marcel Dekker, 1998:120-123.

[2] Wernecke P W. Reciprocating seal process analysis[C]∥11th International Conference on Fluid Sealing. Cannes, France: BHRA, 1991: 119.

[3] Nikas G K. Theoretical study of solid back-up rings for elastomeric seals in hydraulic actuators[J]. Tribology International, 2004, 37(9): 689-699.

[4] Nikas G K, Sayles R S. Nonlinear elasticity of rectangular elastomeric seals and its effect on elastohydrodynamic numerical analysis[J]. Sealing Technology, 2004, 37(8): 651-660.

[5] Nikas G K. Elastohydrodynamics and mechanics of rectangular elastomeric seals for reciprocating piston rods[J]. Journal of Tribology, 2003, 125(1): 60-69.

[6] 陈家照, 黄闽翔, 王学仁. 固体火箭发动机长期贮存下橡胶O形圈泄漏分析[J]. 润滑与密封, 2016, 41(2): 76-80. CHEN Jia-zhao, HUANG Min-xiang, WANG Xue-ren. Leakage analysis on rubber O-ring of solid rocket motor under long-term storage[J]. Lubrication Engineering, 2016, 41(2): 76-80. (in Chinese)

[7] 沈明学, 董峰, 彭旭东, 等. 配副金属表面粗糙度对丁腈橡胶O型圈摩擦学特性的影响[J]. 摩擦学学报, 2016, 36(3):320-325. SHEN Ming-xue, DONG Feng, PENG Xu-dong, et al. Effect of surface roughness of metalic counterpart on tribological characteristics of NBR O-ring[J]. Tribology, 2016, 36(3):320-325. (in Chinese)

[8] 王朝晖, 何康康. O形橡胶密封圈的非线性有限元分析[J]. 航天制造技术, 2016(2):4-8. WANG Zhao-hui, HE Kang-kang. Nonlinear finite element analysis of rubber O-sealing ring[J]. Aerospace Manufacturing Technology, 2016(2): 4-8. (in Chinese)

[9] 魏列江, 韩小霞, 熊庆辉, 等. O形圈密封沟槽倒角半径对密封性能的影响[J]. 液压气动与密封, 2016, 36(3): 72-75. WEI Lie-jiang, HAN Xiao-xia, XIONG Qing-hui, et al. The effect of O-ring seal groove fillet radius on the sealing performance[J]. Hydraulics Pneumatics & Seals, 2016, 36(3): 72-75. (in Chinese)

[10] 谭晶, 梁军, 杨卫民, 等. 滑环式组合密封件的研究(Ⅱ)——阶梯形同轴密封件(斯特圈)的有限元分析[J]. 润滑与密封, 2007, 32(7): 16-19. TAN Jing, LIANG Jun, YANG Wei-min, et al. The study of a sliding ring combined seal ring(Ⅱ)—the finite element analysis of stepseals(Si Te ring)[J]. Lubrication Engineering, 2007, 32(7): 16-19. (in Chinese)

[11] 陈家照, 黄闽翔, 王学仁, 等. 几种典型的橡胶材料本构模型及其适用性[J]. 材料导报, 2015, 29(25): 118-120. CHEN Jia-zhao, HUANG Min-xiang, WANG Xue-ren, et al. Typical constitutive models of rubber materials and their ranges of application[J]. Materials Review, 2015, 29(25): 118-120. (in Chinese)

[12] 李传敏. 往复运动密封分析[D]. 青岛：青岛理工大学, 2010:13. LI Chuan-min. Analysis of reciprocating seal[D]. Qingdao:Qingdao Technological University, 2010:13. (in Chinese)

[13] Nikas G K. Analytical study of the extrusion of rectangular elastomeric seals for linear hydraulic actuators[J]. Proceedings of the Institution of Mechanical Engineers Part J: Journal of Engineering Tribology, 2003, 217(5): 365-373.

[14] 韩传军, 张杰, 黄岗, 等. 往复密封中星型密封圈的密封性能分析[J]. 润滑与密封, 2012, 37(9): 28-32. HAN Chuan-jun, ZHANG Jie, HUANG Gang, et al. Seal performance analysis of a star sealing ring in reciprocating seal[J]. Lubrication Engineering, 2012, 37(9): 28-32. (in Chinese)

Calculation and Simulation of Leakage of Stepseals in Main Piston of Hydro-pneumatic Springs

GUI Peng， MAO Ming， CHEN Yi-jie， GUO Jian-juan， GAO Xiao-dong， NING Dan

(Department of Chassis Components Technology, China North Vehicle Research Institute, Beijing 100072, China)

To study the working stability of Stepseals in main piston of hydro-pneumatic springs in a wide range of temperature, a fluid dynamic seal model is established based on mechanics of materials and hydrodynamics. The theoretical formula of Stepseals leakage is deduced. The effects of temperature, piston velocity, pre-compression ratio and groove dimensions on leakage are analyzed using film pressure data from finite element models. Results show that the increase in piston velocity, the decrease in pre-compression ratio and the increase in groove dimensions lead to more leakage of Stepseals, and higher temperature also causes more leakage in allowable temperature range.

ordnance science and technology; Stepseal; leakage; hydro-pneumatic spring

2016-11-08

国家自然科学基金项目(51305410)

桂鹏(1992—)，女，硕士研究生。 E-mail: guipeng0101@163.com

毛明(1962—)，男，研究员，博士生导师。E-mail: ming_mao@noveri.com.cn

TB42

A

1000-1093(2017)07-1255-08

10.3969/j.issn.1000-1093.2017.07.002