基于无人机GPS的测量雷达标校方法研究

姬新阳 高 山 陈庆良 张海龙 宫福红 范志鹏

(1.中国洛阳电子装备试验中心 洛阳 471003;2.西安卫星测控中心 西安 710043)

基于无人机GPS的测量雷达标校方法研究

姬新阳1高 山2陈庆良1张海龙1宫福红1范志鹏1

(1.中国洛阳电子装备试验中心 洛阳 471003;2.西安卫星测控中心 西安 710043)

测量雷达任务前必须进行标校以消除系统误差，通常使用方位标、距离标和光电综合标等标校设施进行标校，但有些临时阵地并不具备完整的标校设施，此时采用常规标校方法就存在一定的限制。文中通过对标校原理进行分析，设计了一种利用小型无人机加装GPS设备对精测雷达进行标校的方法。通过模拟数据解算证明该方法有效、可行，且得到了该方法的适用航线。该标校方法简便、快捷，具有不受场地和常规标校条件限制的优点。

标校;无人机;GPS;测量雷达

0 引言

通常，雷达测量精度的高低用其测量误差的大小来表征和衡量，测量误差是指测量值与真实值之间的偏差，测量误差小即意味着测量精度高。精密跟踪测量雷达的原始测量数据存在系统误差和随机误差。为提高测量数据的准确度，在数据处理中通过数据平滑滤波来抑制随机噪声;而系统误差则通过标校来修正。因此，标校是精密跟踪测雷达使用维护中的一项经常性工作，准确的标校将有助于修正系统误差，提高雷达测量精度。

目前雷达标校方法主要有常规标校、星体标校和卫星标校三种。在不方便建立常规标校设施，而又不具备星体标校和卫星标校的条件时，如何进行雷达标校就成为一个亟待解决的问题［1－6］。文中通过雷达跟踪带有GPS定位设备的小型无人机，由GPS设备提供的GPS数据作为真值对雷达的系统误差进行标校，可有效解决该问题，同时该方法对地形条件没有要求且不需要常规标校设施，使用范围广。

1 标校原理

1.1 系统误差模型

精测雷达在任务前通常通过标校来减小系统误差，提高雷达测量精度，常规标校方法是通过对方位标和光电综合标，进行大盘水平测试等得到标定参数后，通过系统误差修正公式对测量数据进行修正，消除系统误差。分析时以方位角为例，俯仰角误差与方位角误差类似，不再分析。

雷达测量数据一次误差信息中含有的主要误差有:

(1)方位零值:A0。

(2)大盘不水平产生的方位角误差:

ΔA= θMsin(A － AM)tanE= θMcosAMsinAtanE－θMsinAMcosAtanE，其中θM为最大不水平角度，AM为最大不水平方位角。

(3)方位轴与俯仰轴不正交产生的方位角误差为:ΔA=δntanE，其中δM为方位轴与俯仰轴不正交度。

(4)光轴电轴不平行产生的方位角误差为ΔA=ΔAGD·sec(E)，其中ΔAGD为方位上光电轴偏差。

(5)光轴机械轴不平行方位角产生误差为ΔA=ΔAGJ·sec(E)，其中ΔAGJ为方位上光轴机械轴偏差。

根据以上误差量可以得到方位角误差模型如下:

其中:a0为方位零值;a1、a2为大盘不水平系数;a3为方位轴、俯仰轴不正交系数;a4为光电轴、光机轴和定向灵敏度总误差。

1.2 解算方法

由误差模型可知，如果误差(ΔA，ΔE，ΔR)可以精确测量，就能得到一组数据值 ΔAi，，ΔEi，ΔRi，Ai，Ei，Ri(i=1，2，3，……，m)，将这些数据按照误差模型进行回归分析，通过最小二乘法解算，即可求得各误差系数［6－11］。用矩阵表述如下:

其中:a为误差系数向量

根据求得的误差系数 a0、a1、a2、a3、a4，可以解算出方位零值、大盘不水平度、方位轴与俯仰轴不正交度、光电轴、光机轴和定向灵敏度等标校参数，这样就完成了雷达的标校。

1.3 精度分析

文中标校方法是利用GPS的测量数据提供真值，因此所得标校参数的精度主要取决于GPS的精度和误差模型，应用差分GPS技术时的动态GPS定位精度在0.1米以下，完全可以满足雷达标校要求。

2 标校方法

将GPS定位设备放置在小型无人机上，无人机作为雷达校准时的跟踪目标，GPS定位设备实时的发送GPS数据，地面接收设备实时记录GPS数据。获得GPS数据和雷达测量数据后，首先进行坐标转换，然后进行数据处理，就能得到雷达的系统误差标定参数。

2.1 坐标转换

由于GPS设备测量的是无人机的位置，并不是雷达的直接观测量，在校准前应首先进行坐标变换，将GPS数据转换到雷达站心极坐标下，再进行校准。

转换过程为:由地心大地坐标系依次转至地心空间直角坐标系、站心空间直角坐标系和站心极坐标系［11－12］，地心空间直角坐标系如图1所示。

站心空间直角坐标系的定义为:原点OR位于雷达站点T0，ZR轴与OR(T0)的椭球法线相重合，XR轴垂直于ZR轴指向椭球的短轴，而YR轴垂直于XRORZR平面，构成左手坐标系，目标点TT的坐标表示为(xT，yT，zT)。如图2 所示。

站心极坐标系定义为:以XRORZR平面为基准，以OR为极点，以XR轴为极轴。目标点TT的坐标表示为(rT，αT，βT)，rT为目标点 TT距离观测点 OR的距离。αT为目标点TT在站心极坐标系的方位角，βT为目标点TT在站心极坐标系的俯仰角。雷达探测目标得到的信息一般为站心极坐标系下的坐标。任一点T在地心大地坐标系中的坐标可表示为(B，L，H)，任一点T在地心空间直角坐标系中的坐标也可表示为(X，Y，Z)，这两种坐标相互可以转换［13］。其转换关系如下式。

其中，a为地球长半径:a=6378137m;e为椭球的第一偏心率:e2=0.00669437999013。

使用公式(8)可以将雷达站点T0的地心大地坐标(B0，L0，H0)和目标点TT的地心大地坐标(BT，LT，HT)转换为地心空间直角坐标系的坐标(X0，Y0，Z0) 和(XT，YT，ZT)。

使用公式(9)，根据雷达站点T0和目标点TT的地心空间直角坐标系的坐标(X0，Y0，Z0) 和(XT，YT，ZT)可以求出目标点TT在站心空间直角坐标系中的坐标(xT，yT，zT)。

由于雷达测得的目标信息是站心极坐标系下的坐标，应当使用公式(11)将目标点TT的站心空间直角坐标系坐标(XT，YT，ZT)转换到站心极坐标系下的坐标(rT，αT，βT):

至此，已经完成了地心大地坐标系到站心极坐标系的转换。

2.2 测量数据处理

2.2.1 测量数据随机误差平滑

雷达测量数据通常带有随机误差，需要对测量数据进行平滑处理，以得到满意的结果。平滑计算的目的即消除随机误差，在保证一定精度的条件下，压缩测量数据量，本文采用多项式平滑方法［14］:

设一组测量数据{ti，xi}(i=1，2…，n)(ti为采样时间，xi为测量数据)，设多项式为:

通过最小二乘法原理，使偏差最小，即:

根据求极值方法，将(12)带入(13)，并求偏导数，得出:

一般情况下多项式次数取3次。

2.2.2 异常值的检测与剔除

本文采用外推拟和法进行野值的识别和检验。外推拟和法通常取前4个或5个连续正常的测量数据，采用一阶或二阶多项式进行计算。δ为相应测量量测量误差的均方差。假设连续5个测量数据为:xi－5、xi－4、xi－3、xi－2、xi－1，由最小二乘线形估计外推获

2.2.3 拉格朗日插值方法

由于雷达测量数据与GPS数据的采样时刻和采样频率并不一致，因此，需要将雷达测量数据插值到GPS数据对应时刻，拟采用10阶拉格朗日插值法进行计算，计算公式如下:

当选取的点数少于10个时，舍去该待插值点。

2.3 标定参数解算

标定参数解算采用最小二乘法进行，通过Matlab编程实现。解算时输入雷达测量数据和GPS数据，首先进行野值识别和处理、数据平滑和插值，其次对GPS数据进行坐标转换，最后进行标定参数解算，并利用GPS真值对得到的标定参数进行检验，满足指标要求后，标校过程结束。

3 模拟数据解算结果

由于各种条件限制，缺少以GPS为真值的测量数据，文中采用模拟数据对标校方法进行了检验。模拟数据没有考虑随机误差，通过解算得到了在理想情况下该标校方法的适用范围。

根据对误差模型的分析，参与解算的数据对解算结果影响非常大，一是方位角必须在0°～360°四个象限内均有数据，才能解算出大盘水平误差;二是由于最后一项误差为Z·sec(E)，当仰角E为3°时，sec(E)为1.00137，这样仰角E在3°以下时，最后一项误差Z·sec(E)与零值a0存在合并到一起的可能，也将会导致结算结果不准确。因此，分两种情况进行模拟解算，一是保持仰角数据线性分布在3°～40°不变，改变方位角数据的范围，分析解算结果是否准确;二是保持方位角数据线性分布在0°～360°不变，改变仰角数据的范围，分析解算结果是否准确。模拟解算结果如表1和表2所示。

通过对模拟数据的解算结果进行分析，可以得到该标校方法的适用范围，主要有以下三点:

(1)方位角数据必须均匀分布在0°～360°四个象限内，每个象限内不少于两组数据，每组数据在40个点以上;

(2)仰角数据必须是变化的，最小变化范围为 17°;

(3)仰角最低为6°;

根据以上三点就可以设计出该标校方法的航线范围，一是仰角数据必须是变化的，同时仰角不能低于6°，范围至少为6°～23°;二是方位角数据可以为分段的，但是最少为八段，而且均匀分布在四个象限，每段数据方位角变化范围最小为10度，在条件允许的情况下方位角数据范围越大解算结果越准确。

在实际标校时可以采用小型无人机以雷达为中心，做圆周飞行，同时保持飞行高度连续变化，飞完一周后即可利用获得的数据计算出雷达的系统误差标定参数，完成雷达的标校工作。

表1 保持仰角数据线性分布在3°～40°时的解算结果

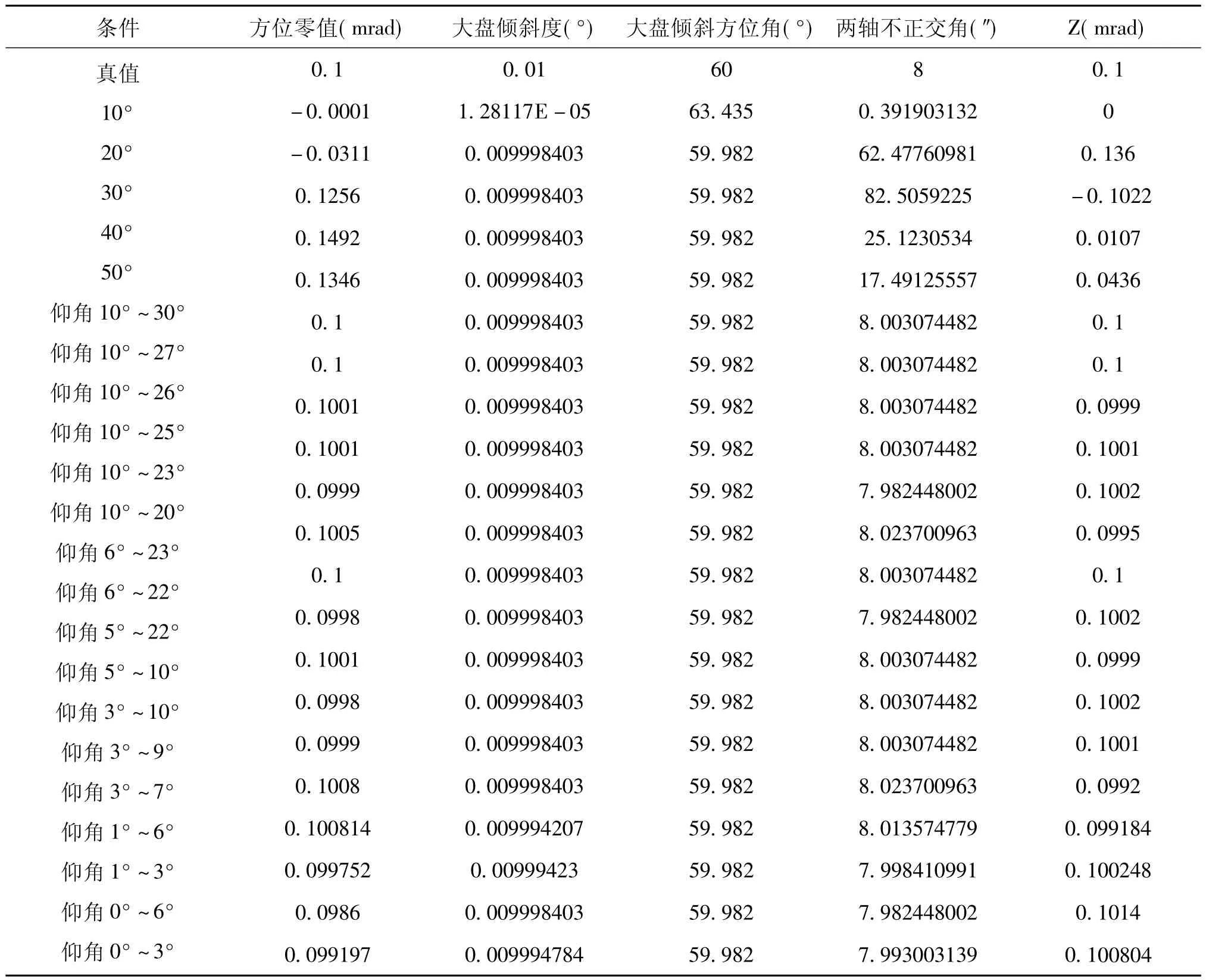
表2 保持方位角数据线性分布在四个象限时的解算结果

5 结束语

通过利用小型无人机携带GPS设备对雷达进行标校，具有不受场地和常规标校条件限制的优点，随着小型无人机技术的发展和成熟，该标校方法对于满足特定场地条件下雷达的标校具有一定的应用前景。

［1］朱起悦.应用差分GPS技术进行雷达标校［J］. 电讯技术，2006，46(1):108 －110.

［2］吴三元，侯志楠，王瑞恒.基于GPS的雷达标校方法［J］.雷达与对抗，2010，30(1):4－6.

［3］杜娟，朱华邦.基于 GPS技术的舰载探测系统标校方法研究［J］.火控雷达技术，2013.，42(1):17－20.

［4］姚景顺，杨世兴.舰载雷达的动态标校［J］.火力与指挥控制，2008，33(3):128－130.

［5］潘绍仁，察豪.基于AIS的舰载雷达标校方法研究［J］.舰船科学技术，2009，31(6):101－104，127.

［6］张舒彦，鲍庆龙，林财永，陈曾平.一种非合作双基地雷达目标跟踪方法科学技术与工程［J］.2015，15(29):153 －157.

［7］丰少伟，黄双华，杨云生.基于差分GPS技术的舰载雷达通用标校方法［J］.现代雷达，2012，34(5):14 －16.

［8］赵罄，王世峰，佟首峰等.舰载雷达零位标校新法［J］.火力与指挥控制，2010，35(2):169－171.

［9］罗军，商允力，曾浩，等.应用AIS信息进行岸基对海雷达标校［J］.电讯技术，2009，49(9):87－89.

［10］姚兆宁.舰载精密测量雷达星体标校方法及应用［J］.现代雷达，1999，(4):8－12.

［11］苑文亮，唐小明，朱洪伟等.基于 ADS－B数据的雷达标校新方法［J］.舰船电子工程，2010，30(3):147 －150.

［12］边少锋，李文魁.卫星导航系统概论［M］.北京:电子工业出版社，2005，02.

［13］寇艳红.GPS原理与应用(第二版)［M］.北京:电子工业出版社，2007，07.

［14］郭军海.基于最优节点样条逼近的观测数据平滑方法［J］.中国空间科学技术，2000，20(3):43－48.

Calibration Method of Measurement Radar Based on UAV with GPS

Ji Xinyang1，Gao Shan2，Chen Qingliang1，Zhang Hailong1，Gong Fuhong1，Fan Zhipeng1
(1.Luoyang Electronic Equipment Test Center of China，Luoyang 471003;2.Xi'an Satellite Control Center，Xi'an 710043)

Measurement radar must be calibrated to eliminate system error before execute the mission，and azimuth，range and optoelectronic integrated calibration facilities are generally used for calibration.But to some temporary positions without complete calibration facilities，calibration by using conventional calibration method is restricted.Through analysis of calibration principle，a calibration method for measurement radar is designed by using UAV with GPS.Simulation result proved that the method is effective and feasible，and suitable route can be obtained.The calibration method is simple and convenient，and is not restricted by site and conventional calibration conditions.

calibration;UAV;GPS;measurement radar

TN953+.5

A

1008-8652(2017)01-073-06

2016-12-11

姬新阳(1989－)，男，工程师。研究方向为测量雷达技术。