一种介质体宽角域散射的快速分析方法

刘召庆 赵 博 刘 博 杨远成

(西安应用光学研究所 西安 710065)

射频仿真 电磁兼容技术

一种介质体宽角域散射的快速分析方法

刘召庆 赵 博 刘 博 杨远成

(西安应用光学研究所 西安 710065)

本文结合渐近波形估计技术(AWE)和体积分方程矩量法(VIE－MoM)快速分析介质体的宽角域散射问题。体积分方程用来对介质目标建模，用四面体元对目标进行体剖分，采用SWG基函数模拟四面体元内的电通量密度。应用矩量法将体积分方程离散生成矩阵方程。目标的雷达散射截面(RCS)高度依赖入射波方向，应用渐近波形估计技术在给定角度对电通量密度进行泰勒展开，采用padé逼近进一步展宽角域范围。最后，数值算例表明渐近波形估计技术结合体积分方程矩量法在介质宽角域散射分析方面的准确性和高效性。

体积分;矩量法;渐近波形估计;宽角域

0 引言

目标的宽角域电磁散射在雷达目标隐身和目标识别等工程应用方面具有重要意义。在电磁计算领域，由于计算机技术的飞速发展，矩量法［1－3］已经发展成为准确预估目标雷达散射截面的重要方法之一。在对介质目标的建模方面，通常会用到两种积分方程，一种是基于面等效原理的 PMCHWT方程［4］，一种是基于体等效原理的体积分方程(VIE)［5－6］。PMCHWT 方程在处理均匀介质体时非常方便，由于对目标进行面剖分，产生的未知量相对较少，然而在处理非均匀介质体时，需要人为的在不同介质分界面处添加边界条件［7］，这在处理任意非均匀介质体时会带来编程上的麻烦。相比而言，基于体等效原理的VIE在对目标建模时需要进行体剖分，同时保证剖分得到的每个体元的电参数为常数，而VIE中包含的面积分一项正是针对不同介质分界面处进行的边界条件处理，因而VIE在分析非均匀介质目标时具有很大的优势。

然而，雷达目标识别工程中要求获得目标的宽角域RCS数据，需要针对每一个入射波方向进行一次积分方程的求解，而这将耗费大量的计算时间。从上世纪80年代末以来，发展出的最佳一致逼近［8］、渐近波形估计(AWE)［9－10］和柯西方法［11］等插值技术，使目标的宽频带分析在计算时间上的效率大大提高。本文将VIE－MoM与AWE相结合用来分析介质目标的宽角域电磁散射，在给定角度对电通量密度进行泰勒展开，进一步通过padé逼近展宽角域范围，可以得到任意角度的电通量密度，从而实现介质目标宽角域散射特性的分析。相比于传统的VIE－MoM逐点计算方法，该方法大大提高了计算效率。

1 体积分方程－矩量法(VIE－MoM)

介质目标通常分为均匀介质目标和非均匀介质目标。对于均匀介质目标的分析可以使用面等效原理或体等效原理，将目标的散射问题转化为求解目标表面的面等效电磁流或目标体内的体等效电磁流，从而使问题得到解决。而对于非均匀介质目标，电磁参数如介电常数ε(r)和磁导率μ(r)是位置的函数，面等效原理无法定义内等效问题，因此对于非均匀介质的等效一般宜采用体等效原理，这要求对目标进行体剖分，本文采用能够较好拟合任意目标物理形状的四面体元对目标进行剖分，并用SWG分域基函数模拟四面体元内的体电流。

1.1 体积分方程(VIE)

考虑自由空间中一个三维任意介质目标受平面波Ei照射后，其所在区域感应出的体电流J产生的散射场为Es。目标的体积和表面积分别用V和S来表示，介质目标的介电常数为ε(r)=ε0εr(r)，磁导率为 μ0(非磁性材料)。本文的时间因子均采用exp(－ jωt)。

根据体等效原理，将目标的散射问题转化为求解分布在目标体内的等效体电流J(r)。对于非均匀介质目标，不同介质的分界面处体电流J(r)的法向分量并不连续，因此为了方便处理，采用电通量密度D(r)作为待求的未知量。关于电通量密度D(r)的体积分方程表达式如下:

其中，k0为自由空间波数，G(r，r')为三维自由空间标量格林函数，κ(r)表示介质材料的介电常数对比率，表达式如下所示，

公式(4)右边的第二项包含对介电常数对比率求梯度的运算，对这一项进行体积分运算，

其中κ+(r')和κ－(r')分别表示组成一个未知量的两个四面体元的介电常数对比率。公式(5)将体积分一项转化成为面积分，这正是VIE自动处理不同介质分界面处边界条件的积分项。

1.2 矩量法求解体积分方程

应用矩量法求解公式(1)所示的VIE，首先用SWG基函数［5］展开电通量密度D(r)如下，

SWG基函数在组成未知量的两个四面体公共面上具有法向连续性，同时在四面体元内其散度为常数。SWG基函数表达式为:

其中，Z和V分别表示N×N维的阻抗矩阵和N维的激励矢量，其元素表达式为:

2 渐近波形估计(AWE)

VIE－MoM生成的矩阵方程中，阻抗矩阵是关于波数k的函数，电通量密度矢量和激励矢量为波数 k和(θ，φ) 的函数，

本文应用AWE在球坐标系下对空间宽角域散射问题进行插值计算，首先考虑θ极化入射波对θ进行扫角的情况。将电通量密度矢量D和激励矢量V对θ进行泰勒展开，

将公式(12)和(13)带入(11)，并做同阶多项式对比，得到:

其中，V(q)(θ0)为激励矢量V在θ0处的q导数，其元素表达式为:

其中，Ei(r)为θ极化入射波，其表达式如下，

公式(16)中的Eθ为θ入射波的幅值为平面波入射的入射方向为球坐标系中θ方向的单位矢量，

求解得到的电通量密度矢量D往往受到其收敛半径的限制，通过padé逼近将泰勒级数转化为有理函数，进一步展宽角域范围，

最后要说明的是，φ极化入射波对θ进行扫角的情况和上面介绍的情况基本一致，区别在于入射波的表达式，并注意到φ方向的单位矢量用直角坐标系表示只有两个分量。

3 数值算例

为验证算法的有效性，给出三个算例的数值结果。所有计算都在主频为2.0GHz的个人电脑上完成，线性方程组的求解均采用LU分解法，数据采用双精度类型存储，AWE的泰勒展开阶数为Q=4，L=M=Q/2。

3.1 均匀介质目标

考虑一个边长0.2m的立方体和半径0.1m的球组成的均匀介质目标，相对介电常数为1.96，球的1/4嵌入在立方体中。500MHzθ极化的平面入射波沿 － z轴方向入射，φ =0°，θ∈［0°，180°］的单站RCS如图1所示。目标剖分为1818个四面体元，3911个未知量。图1中给出了VIE－MoM逐点扫角的RCS，并给出仿真软件FEKO的结果作为对比。VIE－ AWE1为采样角度在θ为45°、90°和135°的三点AWE插值结果，图1可见在θ在12°和180°附近的结果有一定误差。四点AWE插值的VIE－AWE2与VIE－MoM吻合很好，采样角度分别为36°、72°、108°和 144°。

3.2 非均匀介质柱

如图2所示，目标为三个半径0.2m、高0.2m的圆柱组成的三层非均匀介质柱，沿+z轴方向的相对介电常数常数分别为 1.6、1.96和 2.25。300MHzθ极化的平面入射波沿－z轴方向入射，φ=0°，θ∈［0°，180°］的单站 RCS 如图 2 所示。目标剖分产生3009个四面体元，6344个未知量。FEKO和逐点VIE－MoM的计算吻合良好，证明了VIE对于非均匀介质计算的准确性。三点展开(45°、90°和135°)的VIE －AWE 在θ为0°和180°附近有一定误差，四点展开(36°、72°、108°、144)的 VIE － AWE 于逐点计算的结果高度吻合。

3.3 非均匀介质立方体

最后给出一个入射波为φ极化的算例。如图3所示，目标为三个边长分别为0.2m、0.4 m和0.6m的立方体(相对介电常数分别为1.4、1.2和1.69)嵌套组成的非均匀介质目标。200MHz的平面波沿－z轴方向入射，图3 给出了 φ =45°，θ∈［0°，180°］的单站RCS。目标剖分产生1691个四面体，3625个未知量。三点展开(45°、90°和 135°)的 VIE －AWE1在θ为0°和180°附近不够准确，仍为三点展开(25°、90°和 145°)的 VIE － AWE2 具有很好的拟合精度。

表1给出了VIE－MoM逐点扫角和VIEAWE扫角在计算时间和内存上的对比，可以看到在保证精度的前提下，VIE－AWE需要的内存有微小的增加，但在计算时间上具有很大的优势，三个算例在计算时间上分别减少了94.1%、79.1%和93.5%。

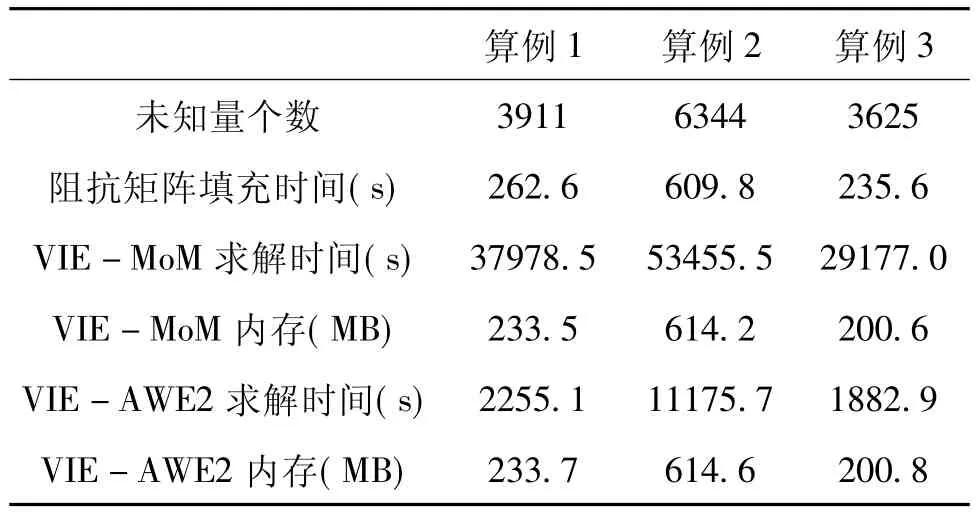
表1 VIE－MoM和VIE－AWE的计算时间和内存需求

4 结论

将AWE技术结合VIE－MoM分析了介质目标的宽角域散射特性。VIE对于均匀介质和非均匀介质目标，均采用四面体元进行体剖分来获取介质体内部的电磁信息，通过矩量法对VIE精确求解。对于宽角域散射特性的分析，需要在给定角度范围内重复求解VIE，为了提高扫角效率，本文结合AWE插值技术很大程度减少了计算所需的时间。数值结果验证了VIE－AWE在求解介质目标宽角域散射特性的准确性和高效性。

参考文献:

［1］王兴，龚书喜，王文涛，等.一种快速分析面面结构电磁辐射特性算法［J］.西安电子科技大学学报，2011，38(4):106 －111.

［2］Zhang Y，Lin Z C，Sarkar T K.Performance of a Massively Parallel Higher-Order Method of Moments Code Using Thousands of CPUs and Its Applications［J］.IEEE Trans.Antennas and Propagat.，2014，62(12):6317－6324.

［3］袁浩波，王楠，党晓杰，梁昌洪.高阶矩量法求解MFIE时近奇异性提取［J］.微波学报，2013，29(1):5 －8+21.

［4］Umashankar K，Taflove A，Rao S M.Electromagnetic Scattering by Arbitrary Shaped Three-Dimensional Homogeneous Lossy Dielectric Objects［J］.IEEE Trans.Antennas and Propagat.，1986，34(6):758 －766.

［5］Schaubert D H，Wilton D R，Glisson A W.A tetrahedral modeling method for electromagnetic scattering by arbitrarily shaped inhomogeneous dielectric bodies［J］.IEEE Trans.Antennas and Propagat.，1984，32(1):77－85.

［6］Nie，X.，et al.Precorrected-FFT solution of the volume integral equation for 3－D inhomogeneous dielectric objects［J］.IEEE Trans.Antennas and Propagat.，2005，53(1):313－320.

［7］Yuan N，Yeo T S，Nie X C，et al.RCS Computation of Composite Conducting-Dielectric Objects with Junctions Using the Hybrid Volume-Surface Integral Equation［J］.Journal of Electromagnetic Waves and Applications，2005，19(1):19－36.

［8］吕政良，龚书喜，张鹏飞，等.快速分析线面结构天线宽带特性的扫频方法［J］.西安电子科技大学学报，2014(1):87－91.

［9］Reddy C J，Deshpande M D，Cockrell C R，et al.Fast RCS Computation over a Frequency Band Using Method of Moments in Conjunction with Asymptotic Waveform Evaluation Technique［J］.IEEE Trans.Antennas and Propagat.，1998，46(8):1229 －1233.

［10］Ma J，Gong S H，Wang X，et al.Efficient Wide-Band Analysis of Antennas Around a Conducting Platform Using MoM-PO Hybrid Method and Asymptotic Waveform Evaluation Technique［J］.IEEE Trans.Antennas and Propagat.，2012，60(12):6048 －6052.

［11］Adve R S，Sarkar T K，Rao S M，et al.Application of The Cauchy Method for Extrapolating/Interpolating Narrowband System Responses［J］.IEEE Trans on Microwave Theory and Techniques，1997，45(5):837－845.

Fast Analysis to Scattering of Dielectric Bodies in Broad Angular Domain

Liu Zhaoqing，Zhao Bo，Liu Bo，Yang Yuancheng
(Xi'an Institute of Applied Optics，Xi'an 710065)

Fast analysis to scattering of dielectric bodies in broad angular domain by combing asymptotic waveform evaluation(AWE)technique and volume integral equation-method of moments(VIE-MoM)is proposed.The VIE is used for modeling of dielectric target，tetrahedron element is used for volume meshing to the target，and SWG basis functions is used to simulate electric flux density in tetrahedron elements.The MoM is used for discretization of VIE to get matrix equation.As radar cross section(RCS)of target is highly dependent on the direction of incident wave，carry out Taylor expansion to electric flux density at the given angle by using AWE;and broaden angular domain further by using padé approximation.Finally，numerical examples demonstrate the accuracy and efficiency of the combination of AWE and VIE-MoM applied to the scattering analysis of dielectric bodies in broad angular domain.

volume integral equation(VIE);method of moments(MoM);asymptotic waveform evaluation;broad angular domain

TN98

A

1008-8652(2017)01-068-05

2016-11-03

刘召庆(1979－)，男，高级工程师。主要研究方向为光电系统总体设计技术、电磁兼容设计技术。