基于量子粒子群方法训练ANFIS模型

张正金 吴剑威

（1 巢湖学院，安徽 巢湖 238000）（2 合肥师范学院，安徽 合肥 230601）

基于量子粒子群方法训练ANFIS模型

张正金1吴剑威2

（1 巢湖学院，安徽 巢湖 238000）（2 合肥师范学院，安徽 合肥 230601）

论文提出一种基于量子行为粒子群算法优化自适应模糊推理系统模型(ANFIS)参数，与之前使用梯度下降方法（Gradient Decent Method）不同，论文使用QPSO方法来训练ANFIS模型中隶属度函数的参数。经过训练后的ANFIS模型可以应用到非线性系统模型和混沌时序的预测。通过几组仿真实验结果表明基于量子粒子群方法训练ANFIS模型要优于基于粒子群算法方法训练ANFIS模型。

粒子群；量子粒子群；模糊系统；ANFIS

1 介绍

模糊系统[1-2]已经成功的应用在了多个领域，例如系统建模和控制。许多神经学习或者统计学习方法中提出了利用自动生成模糊规则的方法来减轻系统的设计并提高系统性能。模糊推理系统采用ifthen规则的模型来对人类知识和推理过程中对那些不能进行精确的定量分析来进行定性的建模。Takagi和Sugeno首次提出模糊建模和模糊识别理论，Kang实际应用于控制、预测和推理过程中[3]。

论文采用基于自适应神经网络模糊推理系统（简称ANFIS）[4]，它可以作为构造模糊if-then规则的依据，来生成一组适当的隶属度函数来生成输入输出对。通过训练过程生成的自适应模糊系统被称为进化模糊系统，也是近些年的研究热点。ANFIS是其中的一个代表。TSK是一个新的方法并且应用于复杂应用。已经证明利用适当的规则，TSK系统可以接近于任何目标。因此，TSK系统已经ANFIS模型中得到广泛应用，具有良好的适应性，它的优点可以用于局部线性化建模和传统线性状态估计与控制技术。

ANFIS同时具有神经网络和模糊系统二者的优点[5]。然而，ANFIS训练参数时遇到的一个主要问题是真值的实际应用。ANFIS最主要的训练方法是基于梯度下降法，在每一步计算梯度时因为使用链式规则可能会导致局部最小值问题。在局部搜索方法使用梯度方法是有效的，其搜索性能也取决于参数的初始值，这样也使得很难找到全局最优的学习速率。模糊系统的设计主要用于解决优化问题，研究人员已经提出在模糊系统设计中使用遗传算法（GA）和粒子群优化算法（PSO）[6]和多粒子协同优化算法[7]。但是由于基本PSO算法不能保证全局的收敛性，孙俊等人提出了基于量子行为的粒子群算法（QPSO）[8]以及改进量子粒子群算法[9-10]。QPSO算法是一种变异的PSO，方法和灵感来源于量子力学。

QPSO的迭代方程优于PSO，它是全局收敛的。除此之外，与PSO不同的是，QPSO不需要速度矢量同时需要更少的参数调整，从而更容易实现。QPSO算法已经成功应用于广泛的连续优化问题。许多实证研究表明，QPSO具有较强的全局搜索能力，解决了许多连续优化问题。

2 模糊系统和ANFIS模型

2.1 模糊系统

本节主要讲述模糊系统在优化方面的研究和数学模型。TSK模糊模型是由Takagi，Sugeno和Kang等人提出的。用形式化的方法来从一个输入—输出数据集中生成模糊规则。Takagi-Sugeno-Kang（TSK）模糊系统能够实现零阶和一阶。第i条规则用Ri来表示，TSK模糊系统的表示形式如下所示：

Rj:if x1（k） is Ai1and…and xn（k） is Ainthen y（k） is fi，i=1，…，r

这里，k 表示的是时间步长，x1（k），…，xn（k） 表示输入变量，y（k）是系统输出变量，Aij表示模糊集合，fi表示相应的功能。模糊集合Aij使用钟形隶属度函数，公式如下所示

其中，ai，bi和 ci是模糊集合Aij的参数，ai表示宽度的一半，bi（连同ai） 用来控制交叉点的斜率，Cij表示隶属度函数相应的中心。在模糊推理机中模糊与运算由模糊理论中的代数积来实现的。因此给出一个输入数据集合 x=（x1，…，xn），第 i条规则的隶属度函数 μ（x）由以下计算得出

对于零阶和一阶TSK类型模糊系统，其相应函数fi分别设置为真值pi0，输入变量的线性函数为假设有在一个模糊系统中有r条规则，则由以下方法进行加权平均后得出系统的输出，

QPSO算法提出在每一个规则中去优化参数ai，bi和 ci。

2.2 ANFIS系统结构的概述

1993年，由Jang首次提出神经模糊网络，即ANFIS模型。ANFIS是自适应网络，节点是自适应的一部分，这意味着它们的输出取决于参数属于这些节点。两种学习算法在训练参数期间去改变参数来优化性能。为了简单起见，系统采用两个输入和一个输出。TSK模糊模型的规则机包含两个模糊if-then规则。一个典型的TSK模糊模型表示的两个模糊规则如下：

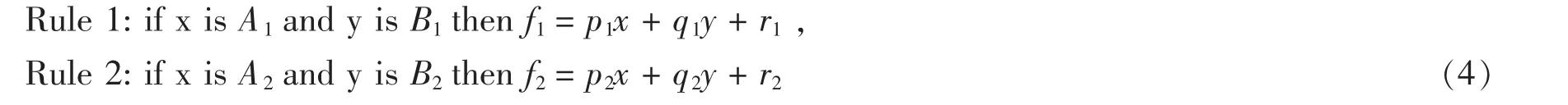
其中，x，y表示ANFIS的输入，A和B表示模糊集合，fi表示一阶多项式，同时也代表了输入一阶TSK模糊推理系统。在上述的规则中，pi，qi和ri表示的是参数集合，也是随之需要讨论的参数问题。ANFIS结构如图1所示，在每一层节点功能如下所述：第一层：这一层节点包含了自适应功能，描述如下：

其中，x，y表示输入节点，A和B表示语言标签，μ（x）和μ（y）表示隶属度函数，通常采用一个钟形来表示最大值是1，最小值是0

其中，ai，bi和 ci是集合参数，随着这些参数值的改变，钟形函数也会发生相应的变化，从而在语言标签A和B方面表现出不同的隶属度函数的形式。事实上任何连续和分段可微函数在这一层都具有河沟的候选节点，如常用的梯形或者三角隶属度函数。参数在这一层称为前提参数。

第二层：这一层为固定节点，节点用圆圈来表示，标记为Π，与节点函数乘以输入信号作为输出输出ωi表示规则的触发强度，节点输出表示模糊规则的触发强度。

第三层：该层为固定节点，节点用圆圈表示，并标记为Ni，每个节点使用归一化函数来计算第i个节点的触发强度除以所有节点的触发强度之和。

方便起见，这一层的输出称为归一化触发强度。

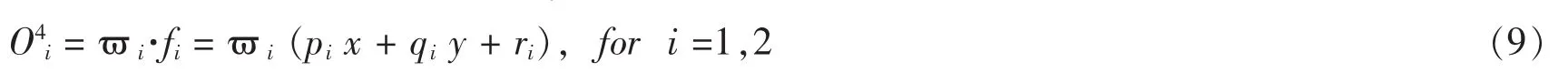
第五层：该层也为固定节点。整体输出用线性组合来表示后件参数。

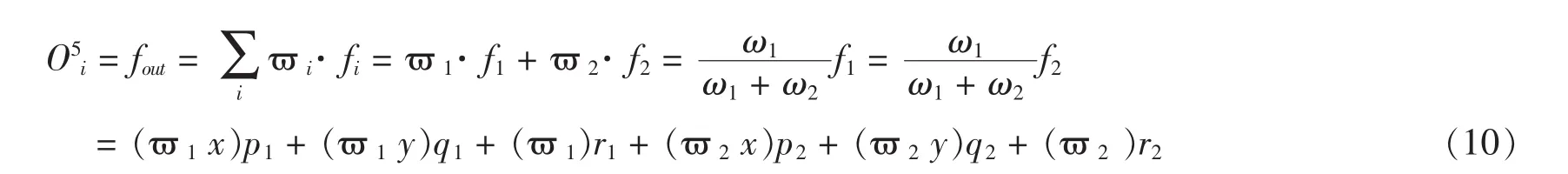
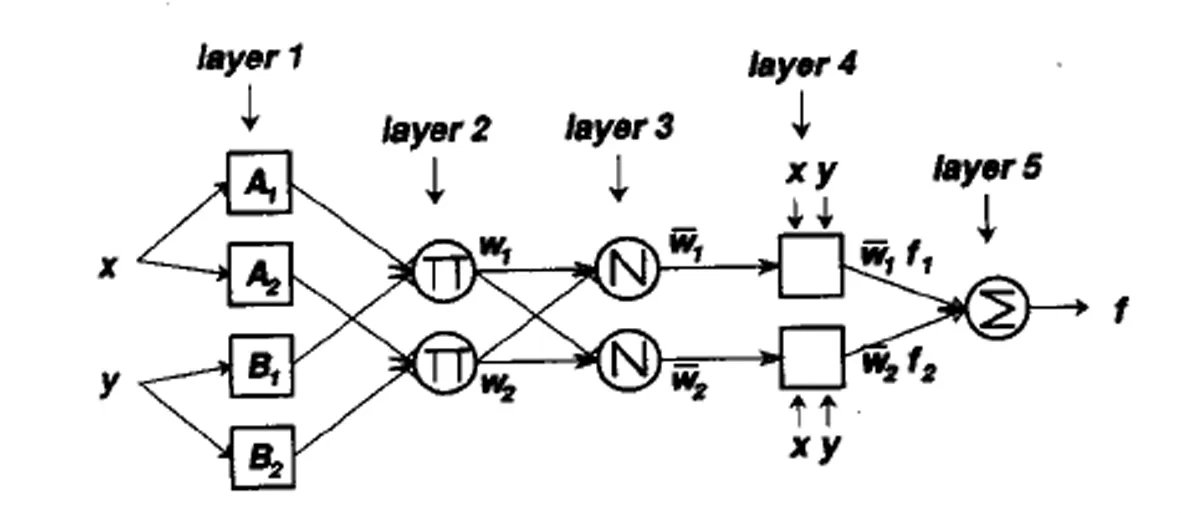
图1 ANFIS结构

2.3 混合学习算法

可以看出有两个可修改的参数集合，即{ai，bi，ci}表示前件参数，{pi，qi，ri}表示后件参数。这种结构的训练目的是通过调整上述两个参数集合来使得ANFIS输出合适的训练数据。每个混合学习算法都是有两个传递：一个向前传递，一个向后传递。在向前传递中，前件参数是为BP算法，利用最小二乘法来确定后件参数。找出最优参数时，固定后件参数并向后传递。输出节点的错误率传播东输出端到输入端，前件参数利用梯度下降法进行更新。

更新前件参数的方法主要使用梯度下降法或者卡尔曼滤波方法，缺点是容易陷入局部最优解。因此，该文主要采用QPSO算法来训练ANFIS参数的目的主要是为了获取全局最优解。

3 量子行为粒子群优化算法

对于M个个体，在PSO算法中，每个粒子在D维空间中被看成是没有质量和体积的，在n次迭代中第 i个粒子的当前位置和速度表示为粒子的移动通过以下方程来完成：

for i=1，2，…，M； j=1，2，…，D， c1和 c2为加速因子，w 为惯性权重，向量Pi，n= （P1i，n，P2i，n…PDi，n）表示群体 i先前最优值的位置，Gn= （G1n，G2n…GDn）表示最优群体的位置和所有群体中全局最优位置，称为最优最优值。不失一般性，我们考虑以下最大化问题：

f（x）是一个连续的目标函数，S是一个可行性空间，因此Pi，n的更新如下：

修建智慧楼宇，实现绿色校园 在很多高校，智慧楼宇可将建筑物的电力、照明、空调、排水、消防、弱电和安保等自动化地进行集中监视、控制和管理，为用户提供安全舒适、便捷高效的工作与生活环境，改变以往的教学楼使用效率不高，有时拥挤、有时闲置，中央空调、照明、电器等能源没有得到及时合理控制，造成很大浪费的情况。通过建设智能教学楼，使整个系统和各种设备处在最佳的工作状态，并保证系统运行的经济性，以及管理的现代化、信息化和智能化，实现能耗的有效控制，减少能源浪费，实现绿色校园，提升和改善师生的校园生活品质。

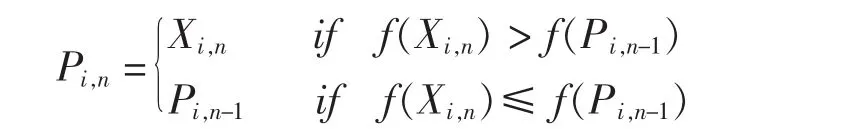
或

在QPSO算法中，每个单粒子被认为在量子空间是受限的粒子。粒子群的状态以波段函数Ψ为特征，其中 Ψ2表示位置的概率密度函数。假设在i个粒子中的在D维空间的第n次迭代中，潜在的中心在第 j维中（1≤j≤D）。 Vji，n+1= Xji，n-pji，n，可以得出在第n+1次归一化的波动函数为

满足的约束条件是如果 Yji，n+1→∞ 那么 Ψ（Yji，n+1）→0。 Lji，n是波段函数的特征长度。 通过波段函数的统计描述，给出的概率密度函数如下：

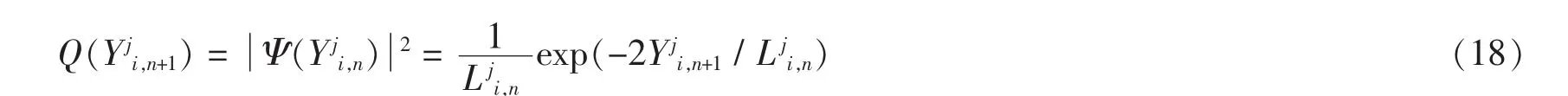
因此概率分布函数如下：

使用蒙特卡罗方法，在第n+1次迭代中可以测量出第i个粒子位置的第j维组成

3.1 量子粒子群算法如下：

步骤1：在空间中初始化粒子群中粒子的位置；

步骤2：计算出粒子群的平均最优位置；

步骤3：计算粒子的当前适应值，并与前一次迭代的适应值比较，如果当前适应于前一次迭代的适应值，则根据粒子的位置更新为粒子当前的位置，即如 f[Xi（t）]＜ f[Pi（t）]，则 Pi（t）=Xi（t）；

步骤 4：计算群体当前的全局最优位置，即 G（t） =Pg（t）， g=argmin {f [Pi（t）]}

步骤5：若当前全局最优位置优于上一次迭代的全局最优位置，则群体的全局最优位置更新为该当前全局最优值；

步骤6：通过对粒子的每一维进行计算得到一个随机点的位置；

步骤7：根据进化公式得出粒子新的位置；

步骤8：重复步骤2-7，直至循环结束。

3.2 量子粒子群优化ANFIS算法过程：

步骤1：迭代次数t=1，初始化粒子群，第i个粒子的位置为Xi（t）；

步骤2：将ANFIS的前件参数设置为每个粒子的位置，然后根据公式（1-6）计算规则的适应度函数wj和归一化适应度值（（1≤j≤l，l为规则数），根据公式计算得出系数矩阵A；然后采用公式（12），计算出后件参数；最后根据公式（14）计算出该粒子所对应的RMSE（即均方根误差），作为该粒子的当前适应度值 fitness（Xi（t））=RMSEi（t）；

步骤3：计算得出粒子群平均最优位置；

步骤4：计算粒子的当前适应值，若优于上一次迭代的适应值比较，则将更新为当前的粒子位置，即如果

f[Xi（t）]＜ f[Pi（t）]，则 Pi（t）=Xi（t）；

步骤 5：计算群体当前的全局最优位置，即 G（t）=Pg（t）；g=argmin{f[Pi（t）]}；

步骤6：若当前全局最优位置优于上一次迭代的全局最优位置，则将群体的全局最优位置更新为当前值；

步骤7：对粒子的每一维，计算得到一个随机点的位置；

步骤8：根据进化公式计算粒子新的位置；

步骤9：重复步骤2-7，直至循环结束。

4 系统仿真实验

接下来将通过两组仿真实验来验证基于量子粒子群算法来训练ANFIS模型的有效性和可行性。实验主要利用非线性系统辨识、多峰函数以及对于混沌时间序列的预测。对于误差分析，这里采用统一的均方根误差（root mean squared error，RMSE）方法，

其中f（i）为实际的输出，f0（i）为模糊系统的输出，n为系统输入输出数据的总个数。

PSO算法和QPSO算法的粒子群规模为50个，QPSO算法的α值从1递减到0.5，PSO算法中的参数设置为三种算法ω=0.7，c1=1.5，c2=1.5，三种算法ANFIS，PSO-ANFIS和QPSO-ANFIS的迭代次数均取为2000次。

模型1：非线性单输入单输出系统

非线性系统方程为：

其中x为输入变量，y为输出变量，在ANFIS模型中，我们取五个隶属度函数，则将会产生五条模糊规则，隶属度函数取为高斯函数，高斯函数中包含两个参数，则我们分别对模糊系统的前件参数的个数设置为10，后件的参数个数也设置为10，同时我们在区间选取100个数值作为模糊系统输入变量x的输入数据。

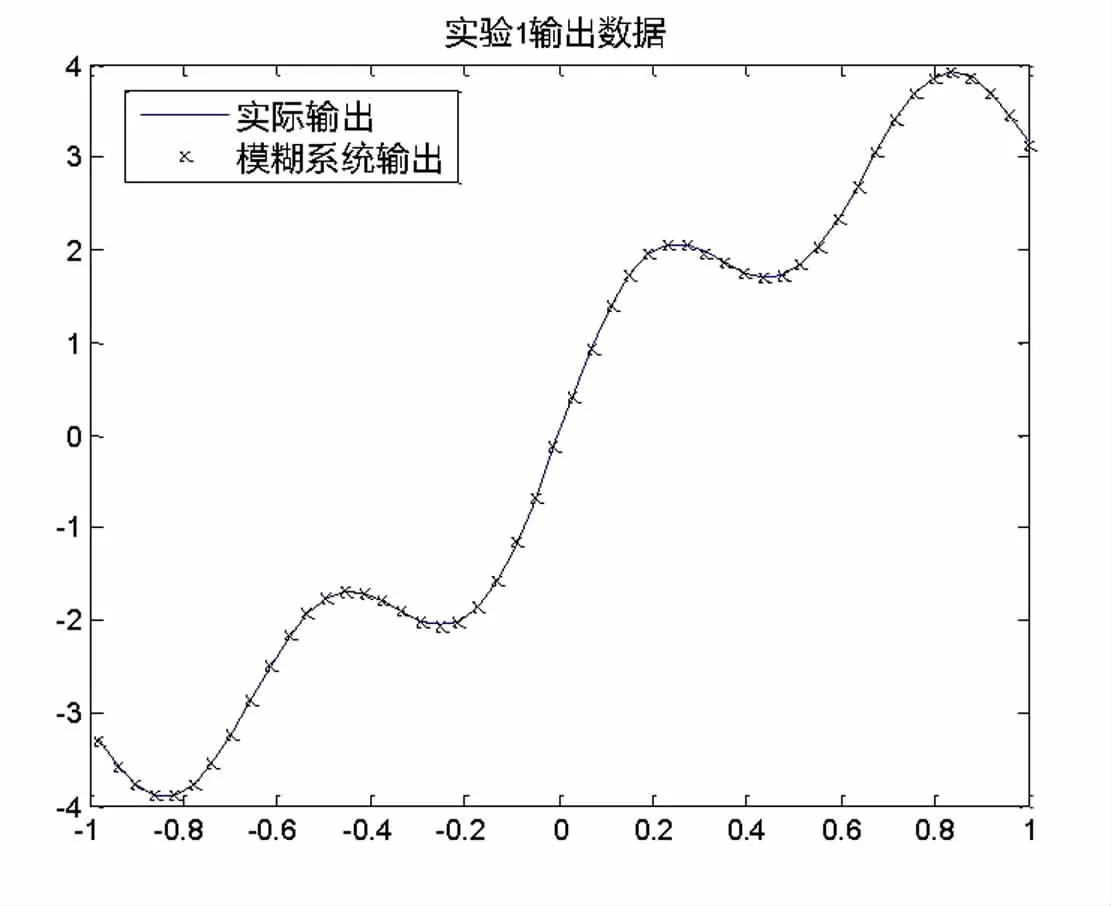
图2 系统实际输出与QPSO-ANFIS输出误差

模型2：非线性多输入单输出系统

非线性系统方程为：

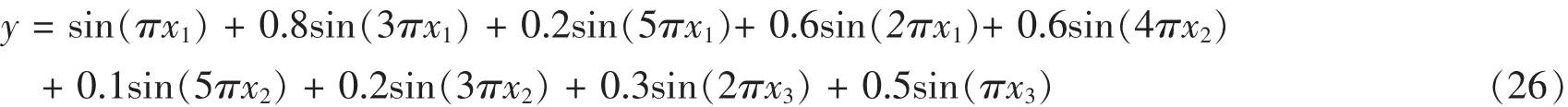
其中x1，x2，x3是非线性系统的三个输入变量，y为输出变量，对每个输入变量分别取两个隶属度函数来进行建模，则该系统是由八条模糊规则组成，隶属度函数取为高斯函数。则我们对该模糊推理系统的前件参数设置为16，后件参数个数也设置为32个。对区间范围[-1，1]×[-1，1]×[-1，1]中选取500个点作为系统的输入数据。对于这500组数据，其中250组用于训练数据，另外250组用于测试。

图3 实际输出与模糊系统输出误差

从表1中所列出的结果可以我们看出，使用了QPSO训练ANFIS模型后的模糊系统的均方根误差要比ANFIS模型的均方根误差要小。如图3所表示的是模糊系统的训练数据误差与模糊系统在QPSO-ANFIS方法后的训练数据的误差。如图4所表示的是模糊系统的测试数据误差与模糊系统在QPSO-ANFIS方法后的测试数据的误差。

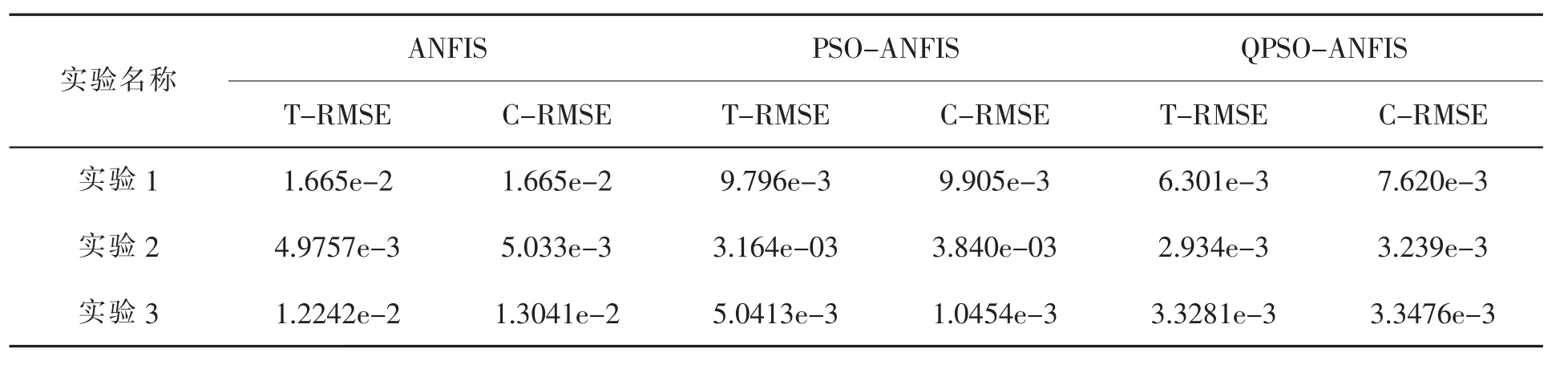
表1 ANFIS，PSO-ANFIS与QPSO-ANFIS数据对比

模型3：QPSO-ANFIS在混沌时间序列中的预测Machey-Glass的微分方程是：

其中 τ为时延参数；t为时间，x（t）为混沌信号

因为初始条件设置的敏感性，这里给定的混沌时间序列的初始值是x（0）=1.2；时延τ=17。取D=4，k=p=6，则对于模糊系统训练数据的输入变量具有如下：

在本次实验的模糊系统训练的输入输出数据形式如下：

data（t） =[x（t-18） x（t-12） x（t-6） x（t） x（t+6）]

其中 x（t-18），x（t-12），x（t-6），x（t）为系统的输入变量，x（t+6）为系统的预测输出。

该非线性系统有4个输入变量，对每个变量分别取2个隶属度函数进行建模。从t=118～1117，可以从中选中选取1000个点作为系统的输入数据。

由此我们得到了1000组符合这一非线性系统关系的数据对，其中前500组用于训练，另外500组用于测试。使用两种算法分别用于识别此非线性系统。三种算法的迭代次数均取为2000次，系统在x（624）～x（1124）的数据与模糊系统在QPSO-ANFIS算法下的预测输出。

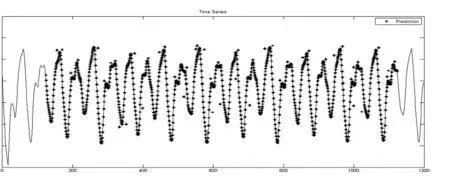
图4 期望输出与QPSO-ANFIS方法下的模糊系统输出对比图

5 结论

在本文中，提出了一种利用量子粒子群算法应用于ANFIS模型中去，同时分别将QPSO应用到不同的输入系统、以及混沌时间的序列预测，根据实验的仿真结果表明，QPSO-ANFIS的误差要明显优于ANFIS和PSO-ANFIS，提高了全局寻优能力。

参考文献：

[1]ZADEH L A.Fuzzy sets[J].Information and Control，l965，（8）:338-353.

[2]王立新.模糊系统与模糊控制教程[M].北京:清华大学出版社，2003:70-98.

[3]谢季坚.模糊数学方法及其应用（第三版）[M].武汉:华中科技大学出版社，2005.

[4]JANG J R.ANFIS:adaptive-network-based fuzzy inference system[J].IEEE Transactions on Systems Man&Cybernetics，1993，（3）:665-685.

[5]张小娟.自适应神经模糊推理系统（ANFIS）及其仿真[J].电子设计工程，2012，（5）:11-13.

[6]李爱国，覃征，鲍复民，等.粒子群优化算法[J].计算机工程与应用，2002，（21）:1-3.

[7]李爱国.多粒子群协同优化算法[J].复旦学报（自然科学版），2004，（5）:923-925.

[8]SUN J，XU W，FENG B.A global search strategy of quantum-behaved particle swarm optimization[C]//Proceedings of the 2004 IEEE Conference on Cybernetics and Intelligent Systems， Singapore， 2004:111-115.

[9]LI P,XIAO H.An improved quantum-behaved particle swarm optimization algorithm[J].Applied Intelligence，2014，（3）:1-3.

[10]CHEN W，ZHOU D，SUN J，at el.Improved quantum-behaved particle swarm optimization algorithm based on comprehensive learning strategy[J].Control&Decision,2012，（27）:719-712.

A STUDY ON TRAINING ANFIS MODEL BASED ON THE METHOD OF QUANTUM PARTICLE SWARM

ZHANG Zheng-jin1WU Jian-wei2
（1 Chaohu College， Chaohu Anhui 238000）（2 Hefei Normal University， Hefei Anhui 230601）

This paper proposes a parameter of self-adaptive fuzzy inference system （ANFIS） based on quantum particle swarm optimization algorithm, different from the previous Gradient Decent Method. It uses Quantum-behaved Particle Swarm Optimization （QPSO） method to train the parameters of membership function in ANFIS model.The ANFIS trained by the proposed method can be applied to nonlinear system modeling and chaotic prediction.The several simulation results show that training ANFIS model based on QPSO method performs much better than the original Particle Swarm Optimization （PSO）method.

Particle swarm；Quantum particle swarm；Fuzzy system；ANFIS

TP399

A

：1672-2868（2017）03-0042-08

责任编辑：陈 侃

2017-03-05

巢湖学院校级科研项目（项目编号：XLY-201613）；国家自然科学基金项目（项目编号：11401056）

张正金（1985-），男，安徽合肥人。巢湖学院信息工程学院，助教。研究方向：模糊系统与进化计算。