基于细观混凝土模型的时间逆转损伤成像方法1)

赵国旗仇亚萍 骆英 冯侃

(江苏大学土木工程与力学学院，江苏镇江212013)

生物、工程及交叉力学

基于细观混凝土模型的时间逆转损伤成像方法1)

赵国旗2)仇亚萍 骆英 冯侃

(江苏大学土木工程与力学学院，江苏镇江212013)

提出了一种针对混凝土结构损伤检测的时间逆转损伤成像方法.以检测混凝土结构中与骨料尺寸相近的微小损伤为目的，引入细观混凝土随机骨料模型，该模型将混凝土结构视为由水泥浆基底、骨料及粘接层组成的三相复合材料，基于Monte Carlo随机样本原理并结合真实试件的骨料级配曲线建立.在数值模拟分析中，将生成含损伤的细观模型导入有限元分析软件进行超声波场模拟，同时采用自适应性强的时间逆转模型(time reversedmodel,TRM)进行损伤定位.TRM分为正向检测和逆时成像两个部分：正向检测过程得到包含损伤的一系列散射回波信号，从数值角度进行时间反演并作为逆时过程的输入信号；逆时成像过程选用等效弹性参数模型，几何尺寸与随机骨料模型相同，时反信号在相应几何位置同时加载形成时反波场，时反波场在损伤位置会发生干涉叠加从而导致能量峰值的出现,通过确定干涉峰值时刻,并获取该时刻对应原始波场以及小波变换能量场完成成像.与原始数据波场图相比，小波变换处理成像结果消除了杂波干扰，成像结果更加清晰.进一步对等效弹性参数的取值进行讨论，并且在骨料尺寸范围内调整损伤大小，结果显示成像结果匹配度高，对于非均质混凝土结构的损伤检测能很好满足损伤定位需求.由此证明，时间逆转成像方法对于具有复杂结构的混凝土材料的损伤检测具有较好的适用性.

混凝土结构，细观模型，时间逆转法，超声检测，损伤成像

引言

当前国家经济发展快速，基础建设规模空前，从楼房、桥梁到机场、海港，其数量与日俱增，而混凝土正是这些基础设施的重要组成部分[1].混凝土结构内部在生产和使用过程中易产生损伤，损伤的积累将导致结构失效，从而诱发灾难性事故.无损检测技术成为目前预防灾难性事故的重要手段.

先前的损伤检测研究将混凝土视为均质材料，在有限元软件模型库中采用平均化参数处理方法；然而当结构中损伤的尺寸与骨料相近时，平均化处理会引起检测精度降低.基于细观力学为背景的细观混凝土模型已经取得重大成果，细观模型从细观尺度出发将混凝土结构视为由骨料、基底及粘接层组成的复合材料.在早期研究中以Wittmann等[2]的二维模型以及Schlangen等[3]的格构模型模拟了混凝土不同组分的力学特性.近年来混凝土细观分析的基础是生成形状、尺寸、位置分布都相似于真实混凝土粗骨料的随机骨料结构，文献[4-5]分别对圆形骨料及椭圆形骨料的生成方法和投放技巧进行了报道；Wang等[6]较早提出随机骨料模型并进行有限元网格的划分；马怀发等[7]依据Walaraven公式生成二维二级配和四级配混凝土随机骨料模型；杨华等[8]对随机骨料模型的混凝土弹性模量的确定进行了预测性研究.本文研究将细观随机骨料模型引入无损检测以提高检测精度，结合超声检测技术完成损伤定位成像.

近年来，超声检测技术由于具有能量高、穿透力强、检测速度快以及安全方便等优点，逐渐成为国内外研究机构关于混凝土无损检测的研究重点，并得到广泛应用.超声波用于混凝土检测始于1949年，Leslie和Cheesman[9]首次采用超声脉冲检测混凝土结构缺陷;然而由于实验局限性，诸多影响因素在当时未得到验证，因此未能用于实际工程检测.21世纪以来，随着电子技术的发展,超声检测技术进入数字时代，数值仿真模拟技术的突破促使超声成像技术得到进一步发展，其中合成孔径聚焦技术[10-11]、超声相控阵技术[1213]、层析成像技术[14-15]等都取得了一定成果.时间逆转技术由于其自适应性特点逐渐由地球科学领域推广到无损检测领域(nondestructive testing,NDT).邱雷等[16-18]针对复合材料板结构检测中存在的信号信噪比低、频散以及模式混叠问题提出了时间反转聚焦成像法,有效提高了有用信号能量.Zhu等[1921]对Lamb的时逆聚焦技术提出了基于频率--波数域内的快速成像法.近年来,将时间逆转技术应用于混凝土检测的尝试逐渐引起学者关注.时间逆转模型(time reversedmodeling,TRM)是探测地球物理学中一项波源定位技术[22].Saenger等[2326]将TRM技术应用于多相高散射混凝土复合材料的检测，TRM被用于对声发射源进行定位和定性，与之前的检测技术相比无需进行首时识别或预知检测通道的相关信息.

为了弥补先前研究中将混凝土视为均质材料而造成的仿真实验实用性不足的缺陷,本文依据真实试件的骨料级配曲线建立更具有实际应用价值的细观混凝土模型，结合有限元软件进行模拟，采用TRM技术完成损伤检测.同时对比不同成像条件结果的精确性，提出更适用于实际混凝土结构检测的损伤成像方法.

1 时间逆转成像法

时间逆转成像法包含正向检测和逆时成像两个步骤：正向检测过程完成损伤信号的采集，采用单点激励信号得到正向波场及损伤散射波场，通过边界传感器接收散射回波信号；逆时成像过程是从数值角度将损伤散射信号在时域内反转并在相同位置加载，依据波前干涉叠加确定损伤位置.

1.1 正向检测

确定检测区域Ω，边界表示为∂Ω，以x∈Ω表示检测区域中的位置.检测时域确定为t∈[0,T]，T为终止时间.正向检测过程用来获取边界一系列位移场时域信号

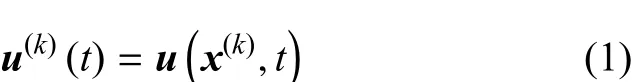
式中，x(k)代表传感器位置，k为传感器编号.

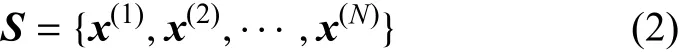
式中，N为边界传感器的个数[25].若加载点与损伤间的距离为L，传感器与损伤间的距离为Lk，传感器接收到损伤散射信号的时间为tk=(L+Lk)/vp，其中vp为纵波波速.

1.2 逆时成像

逆时过程采用等效弹性参数模型[2627]，模型参数由正向检测过程实际测试得到，包括纵波波速vp,eff、横波波速vs,eff以及密度ρeff.正向检测过程中边界∂Ω记录的位移信号为

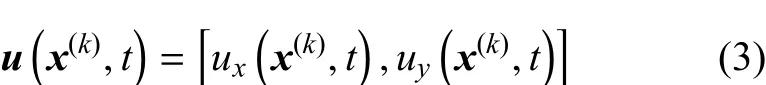
式中,t∈[0,T].将位移信号在时域内取反

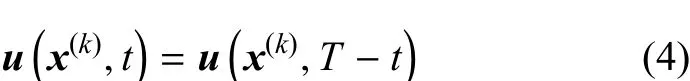
时反信号将作为逆时成像过程的激励信号.正向检测过程记录的k组信号所对应的几何位置将作为时反信号加载的位置，k组信号同时加载形成时反波场.信号中包含的损伤散射信号拥有同一个波源即损伤，该损伤又称二次波源.时反处理后，传感器加载的损伤散射信号到达损伤位置时间为

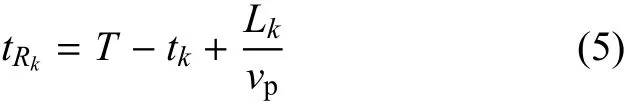
将tk=(L+Lk)/vp代入式(5)得tRk=T-L/vp，由此可见,时反过程中损伤散射信号回到损伤位置所用的时间与各个时反加载点几何位置无关，仅与正向加载点与损伤的几何位置以及波速有关，则k组损伤信号将同时回到波源,形成波前干涉,造成能量叠加.

1.3 成像条件

为了更好地呈现时反波场中的波前干涉叠加现象，引入成像条件进行干涉情况表征和损伤位置确定.全时域全场位移最大值成像[28]

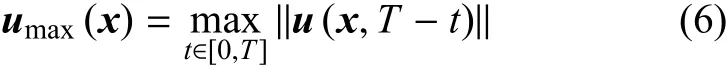
最大位移值umax(x)为时反波场中每一点x∈Ω在t∈[0,T]内的位移最大值.此外，另提取时反应力场，依据全时域应力最大值成像

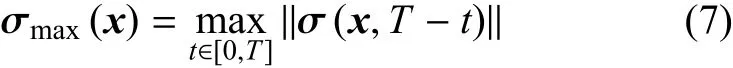
式中，最大应力值σmax(x)为时反波场中每一点x∈Ω在t∈[0,T]内的应力最大值.由于时反加载过程仅选取来自边界数量有限位置上的信号，受杂波干扰会造成难以识别损伤信号形成的汇聚点，引入表征物理特性总和的能量场成像法[28]

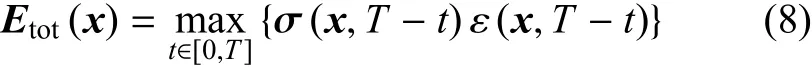
式中，在全时域内网格点处读取应力、应变，文献[29]证明了能量法对于混凝土中声发射源的定位最为精确.

然而针对本文中混凝土损伤的主动检测问题，由于正向检测过程中提取的损伤散射信号比直达波、边界反射波微弱，加上混凝土结构对波形衰减严重[30]以及边界临近传感器加载时会形成波形混叠等因素，全时域内成像结果并不理想.若能获取时反波场中损伤散射信号的干涉叠加产生峰值时刻对应的波场，便能显著提高对损伤位置的确定精度.因此，本文提出单时刻波场成像法，为了准确定位能量聚焦的位置，对波场中各检测点采用小波变换法提取中心频率对应的能量幅值，并确定对应的最大幅值出现时刻te,max，同时获取该时刻时反波场以及小波变换能量场

成像定位误差用下式进行表征

式中,∆L表示定位位置与真实损伤之间的距离，Rmax为混凝土结构中骨料的最大粒径.

2 细观混凝土模型的建立

从专注层面以及研究方法等侧重点的不同，研究过程中将混凝土结构分为3个尺度：宏观尺度(macro-scale)、细观尺度(meso-scale)以及微观尺度(m icro-scale)[31].当检测损伤尺寸与骨料尺寸相近时，选取细观角度分析更为精确.

混凝土骨料的分布是随机的，依据Monte Carlo[32]法进行随机数的生成.生成的骨料采用经典最大密实度曲线指导尺寸以及各尺寸对应的数量分布

其中，D0为筛选直径，p为经过D0筛选的骨料所占的质量百分比，Dmax为骨料最大粒径.根据上式，Walraven推出二维截面内D＜D0粒径骨料出现的概率[33]计算公式

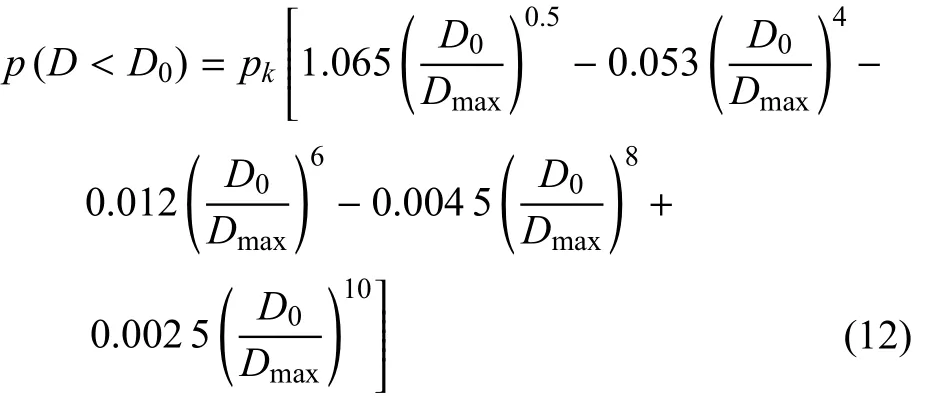
式中，pk为骨料体积占总体积百分比.据此可得出横截面上骨料分布情况.本研究采用MATLAB软件生成具有随机骨料尺寸和随机骨料分布的混凝土模型.

2.2 模型生成实例

依据实际混凝土试件,骨料粒径为10mm～40mm,水泥富余系数为1.08，水、水泥、砂和石子之间的比例为0.42：1：1.152：2.449；混凝土试件整体尺寸大小为400mm×500mm×500mm，据此试件相关参数建立混凝土剖面--损伤--传感器二维截面模型如图1所示.

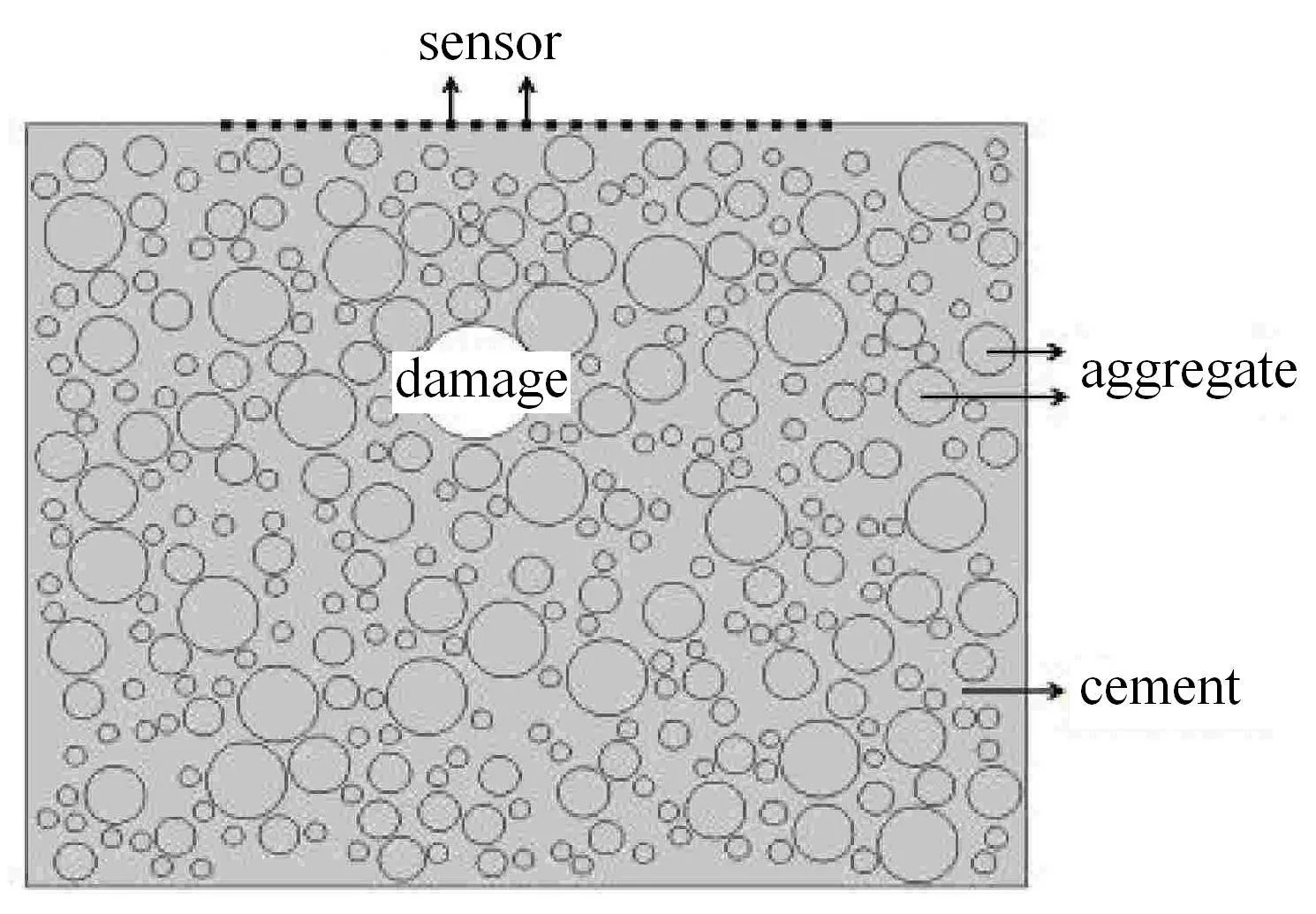
图1 细观混凝土仿真模型Fig.1 Meso-scale concretemodel

将模型导入有限元软件进行参数设定，模型尺寸为500mm×400mm，设定损伤位置为圆形通孔损伤，中心位置在(225,265)mm处，半径为r=30mm.假设传感器为点源，坐标(150,400)mm至(300,400)mm每间隔12.5mm设置一个传感器,编号为1～13.模型主要材料参数如表1所示.

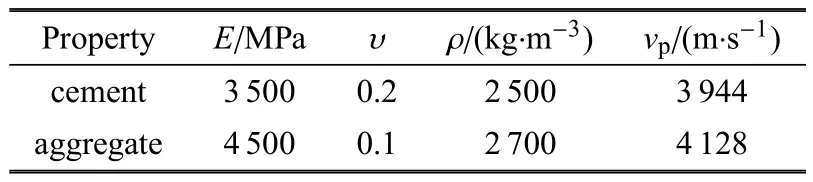
表1 混凝土仿真模型主要参数Table 1 Main propertiesof the concretemodel

3 数值仿真及损伤成像

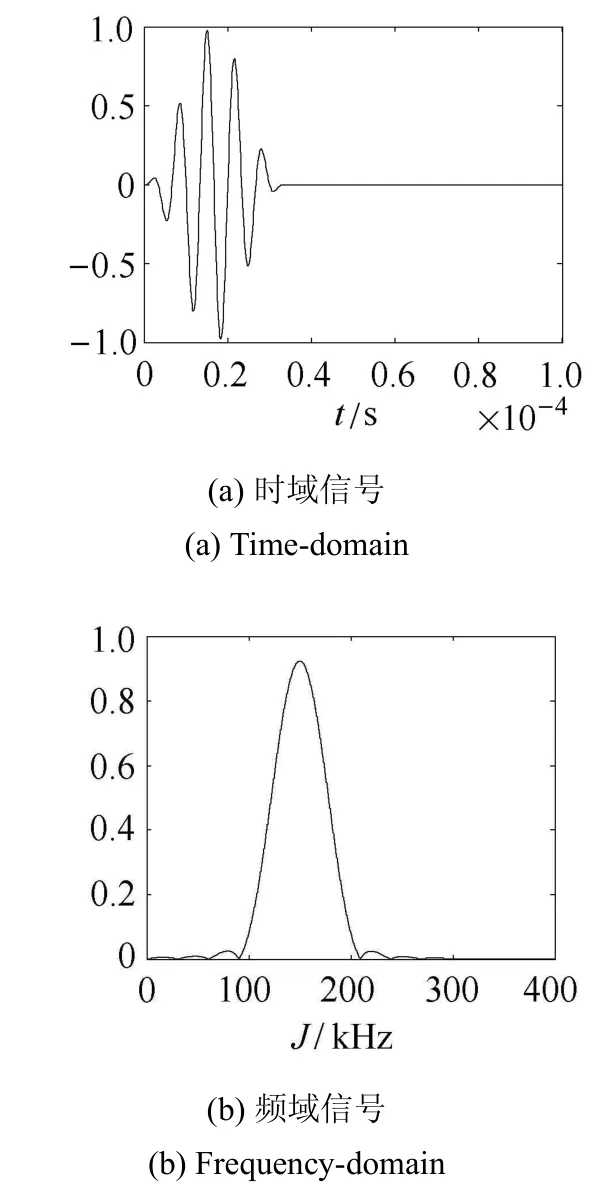
图2 激励信号Fig.2 Excication signal

3.1 仿真成像

(2)因为所以AE=OF=FB′．所以EO=EB′．因而点O在⊙E上．所以从而∠BAC=∠BED．所以DE∥CA．

将建立的混凝土随机骨料模型导入COMSOL Multiphysics 5.1有限元软件建立如图1所示的混凝土剖面--损伤--传感器模型，选用7号传感器作为激励源进行单点激发多点接收模式.激励信号为Hanning窗调制的五周期正弦信号，如图2(a)所示，以等效力形式加载;图2(b)为激励信号对应的频谱.由于纵波波长最大为27mm，为保证数值计算的从而出现汇聚点.

但由于正向检测过程中提取的损伤散射信号较直达波、边界反射波微弱，再加上混凝土结构对波形衰减严重以及边界临近传感器加载时信号会在边界及路径中出现不同形式的混叠，损伤位置之外在边界以及路径中也出现了像素亮点，致使全时域内成像结果并不理想.因此，本文提出基于小波变换的单时刻波场成像法，选取波形干涉出现能量峰值时刻的全场波形来进行损伤成像，所选基函数为Gabor小波,该基函数可以同时提供时域和频域局部化的信息[34].稳定性与准确性，故设置模型网格单元尺寸不大于3×10-4m，时间步长为0.5µs.

激励源进行信号激励形成正向波场和损伤散射回波，全部传感器采集信号.波形中主波包主要由直达波、损伤散射回波、边界反射波组成，根据波速以及模型几何尺寸关系，截取仅包含以直达波和损伤散射回波为主波形的信号(t∈[0µs,150µs]).

逆时成像过程选用等效弹性参数模型，几何尺寸与随机骨料模型相同，采用软件ANSYS 14.0建立，依据文献[26-27]进行等效参数的获取，纵波波速vp,eff=4030.5m/s、横波波速vs,eff=2586.3m/s以及密度ρeff=2600kg/m3.网格尺寸为2mm，波场传播时间与信号时间窗值均为T=150µs.时反处理后的13组信号在相应几何位置同时加载形成时反波场.分别得到时反位移场、时反应力场和时反能量场信息.

图3(a)～图3(c)分别为依据式(6)～式(8)的成像结果，图中每个像素点的值为该点上对应全时域内的场量最大值；由于时反信号中损伤回波形成的波包在同时刻汇聚于损伤位置形成波前干涉叠加，

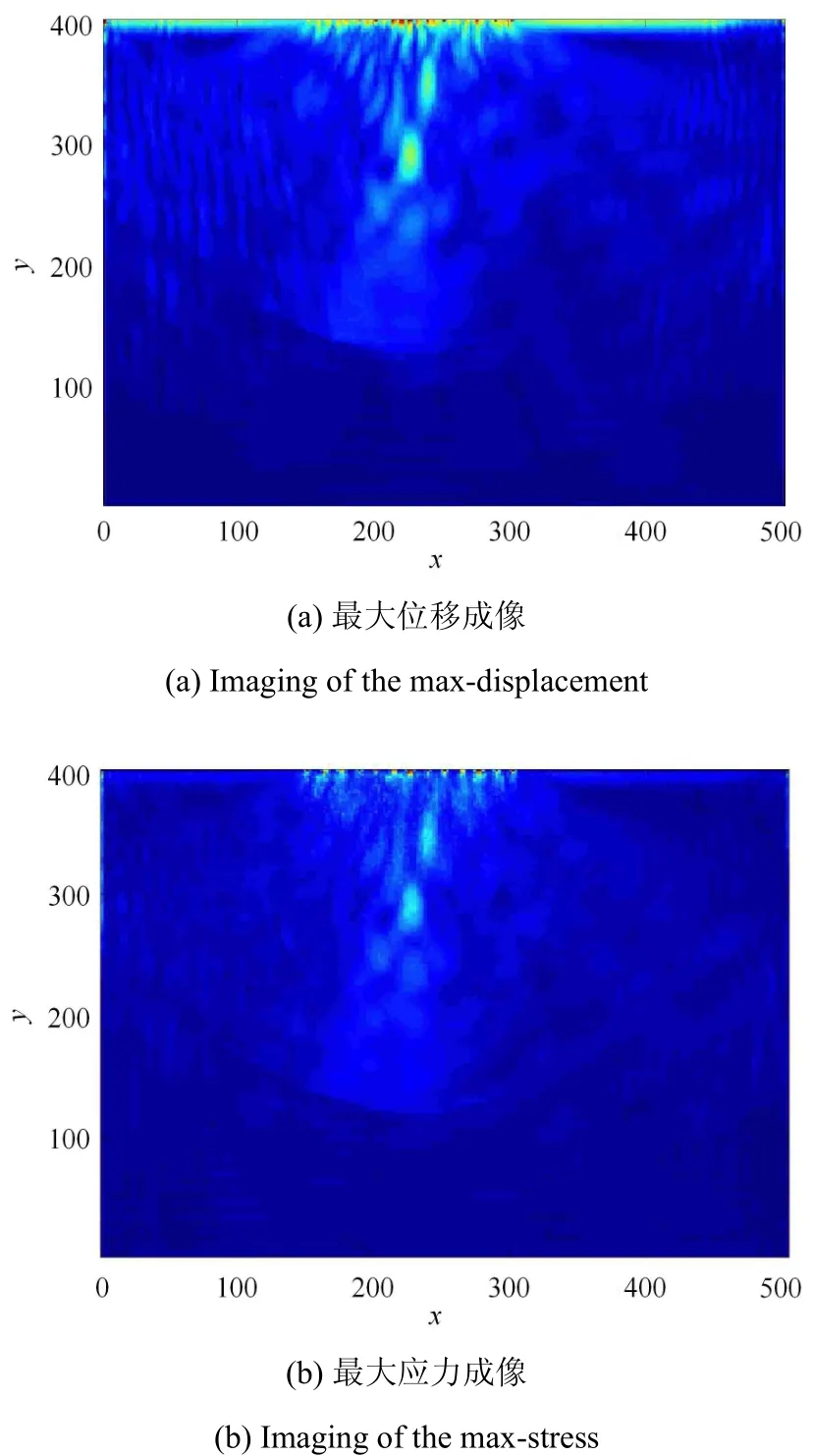
图3 全时域成像Fig.3 Whole time domain imaging

基于小波变换的峰值时刻波场成像法的主要步骤如下：(1)首先对波场中各检测点采用小波变换提取加载主频率f0=150kHz对应的信号幅值，基于小波变换后的全场数据进行最大幅值出现时刻te,max的识别.如图4(a)所示，横坐标表示时间，时域T=150µs，步长为0.5µs；纵坐标表示每一时刻对应全场的能量最大值，最大峰值左侧出现的第一个峰值是由波形在边界处的混叠造成，全场最大能量出现时刻te,max=109.2µs;(2)获取该时刻对应原始数据波场图.本文中为了提高计算效率采用间距2mm的网格点，成像过程为提高精度采用插值处理.如图4(b)所示，图中显示了波形在该时刻的干涉叠加，同时也出现了杂波干扰，图像聚焦点对应实际坐标(223.9,289.5)mm；(3)对峰值时刻小波变换数据进行成像,如图4(c)所示，图像聚焦点对应实际坐标(224.8,291.0)mm.

在正向检测过程中损伤回波信号是由于损伤外表面反射引起，由结构边界特定位置布置的传感器采集得到.损伤表面被认为是二次波源，时反过程中信号在波源处干涉叠加，实际损伤反射点坐标为(225,295)mm；检测结果与实际损伤位置相差4.005mm，根据式(10)进行误差表征，误差为10.01%，成像结果准确地匹配了损伤上表面位置，与原始数据波场图相比，小波变换后的数据成像结果消除了杂波干扰，成像结果更加清晰.

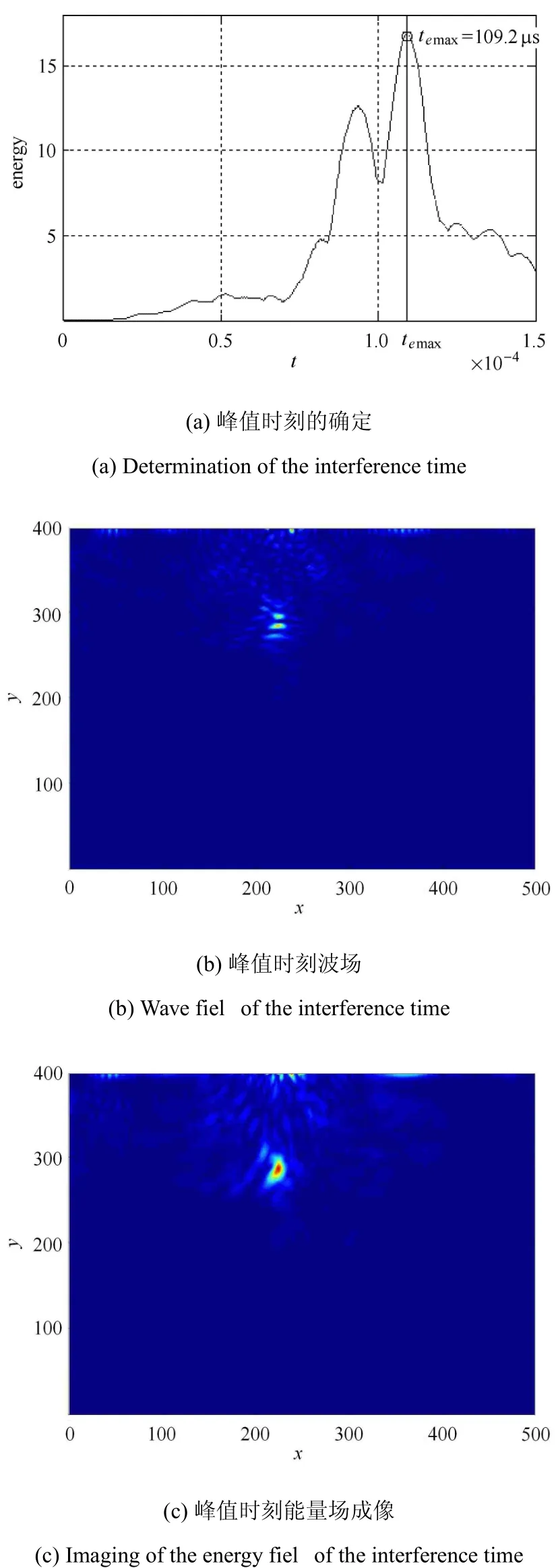
图4 能量场成像图Fig.4 Image of theenergy fiel

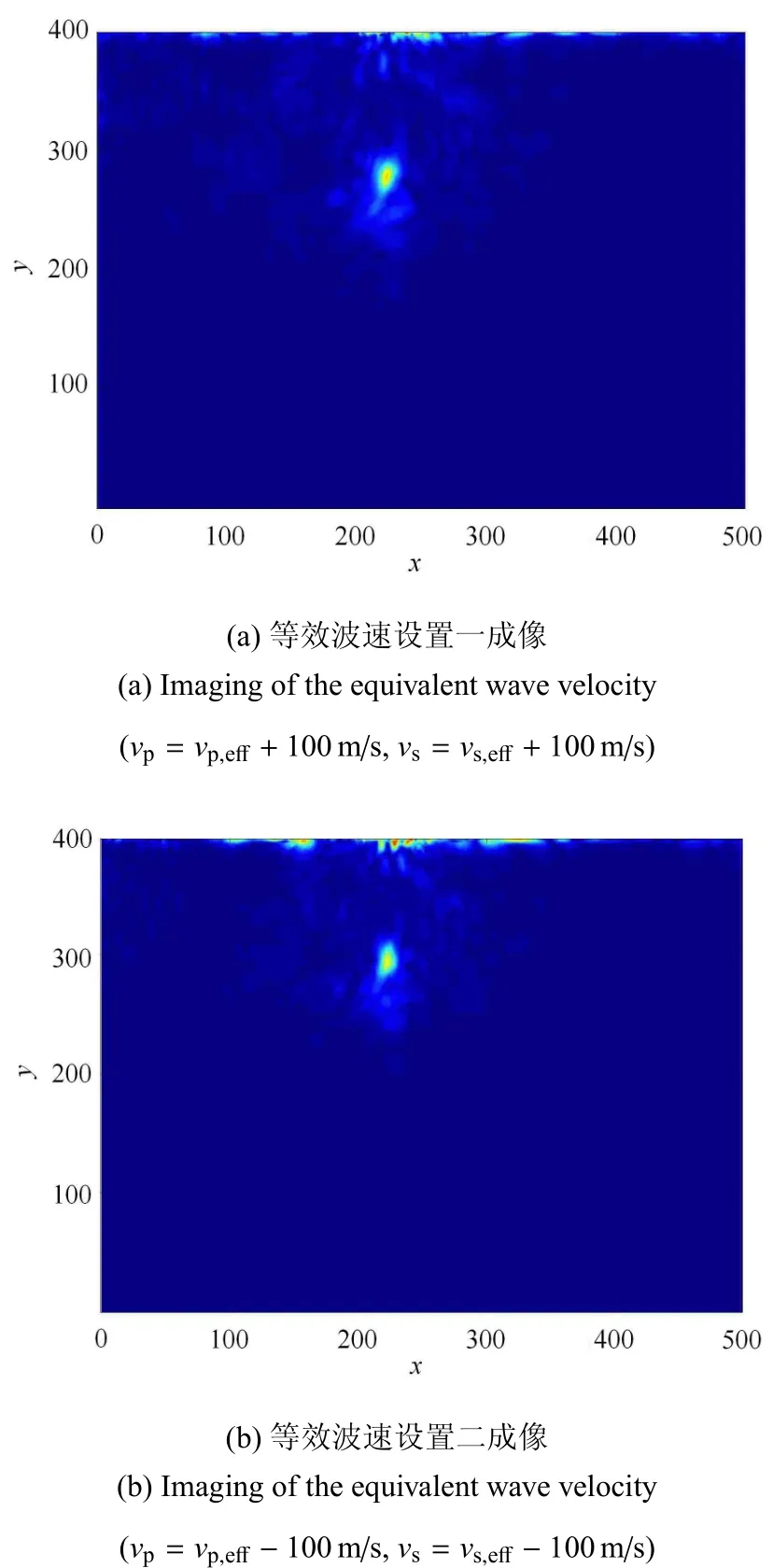
图5 不同等效参数成像结果Fig.5 Damage imaging of di ff erentequivalentparameters

3.2 关于等效参数取值及成像精度的讨论

原始模型为非均质结构，与实际结构相比，均匀化等效弹性参数的取值可能引起损伤定位误差.现依据文献[23]的方法讨论等效波速取值对损伤定位精度的影响，对波速等效分别设置为：(1)vp=vp,eff+100m/s,vs=vs,eff+100m/s；(2)vp=vp,eff-100m/s，vs=vs,eff-100m/s.

图5(a)为设置一的模拟结果，时反波场数据经小波变换后能量峰值出现时刻为te,max=114.5µs，该时刻成像聚焦点坐标为(222.7,278.9)mm，实际损伤位置间距为16.1mm，据式(10)计算误差为40.25%；图5(b)为设置二的模拟结果，能量峰值出现时刻为te,max=111.8µs，该时刻成像聚焦点坐标为(221.7,297.4)mm，实际损伤位置间距为4.08mm，误差为10.2%.结果显示,损伤定位点并没有出现大的偏移，边界传感器一定程度上平衡了参数取值的差异性误差.

本文研究的时间逆转损伤成像方法以检测骨料粒径尺寸范围内的损伤为目的，适用于“不密实区”及“空洞”类型缺陷的检测；此类缺陷一般是由于石子架空现象造成，即损伤尺寸与骨料石子尺寸相近，属于微小型缺陷.

本文选用的混凝土结构骨料粒径为10mm～40mm，故缩小损伤直径d为40mm和20mm，成像结果见图6.图6(a)焦点坐标为(226.1,274.1)mm，对应损伤实际坐标为(225,285)mm，间距为10.95mm，误差为27.3%.图6(b)焦点坐标为(224.1,260.1)mm，对应损伤实际坐标为(225,275)mm，间距为15.02mm，误差为37.5%.

从图6可看出，损伤成像结果精度随损伤尺寸的减小而降低，当损伤尺寸小于骨料平均尺寸(27.63mm)时，成像焦点识别度降低(图6(b))，当损伤尺寸小于骨料最小尺寸时,成像结果将无法识别.然而对于非均质混凝土结构中“空洞”型损伤的检测，本文的定位结果已满足损伤定位需求.由此证明了时间逆转模型损伤检测法及基于小波变换的单时刻成像方法对于具有复杂结构的混凝土材料的损伤检测方法依然具有较好的适用性,且操作简便、结果清晰.

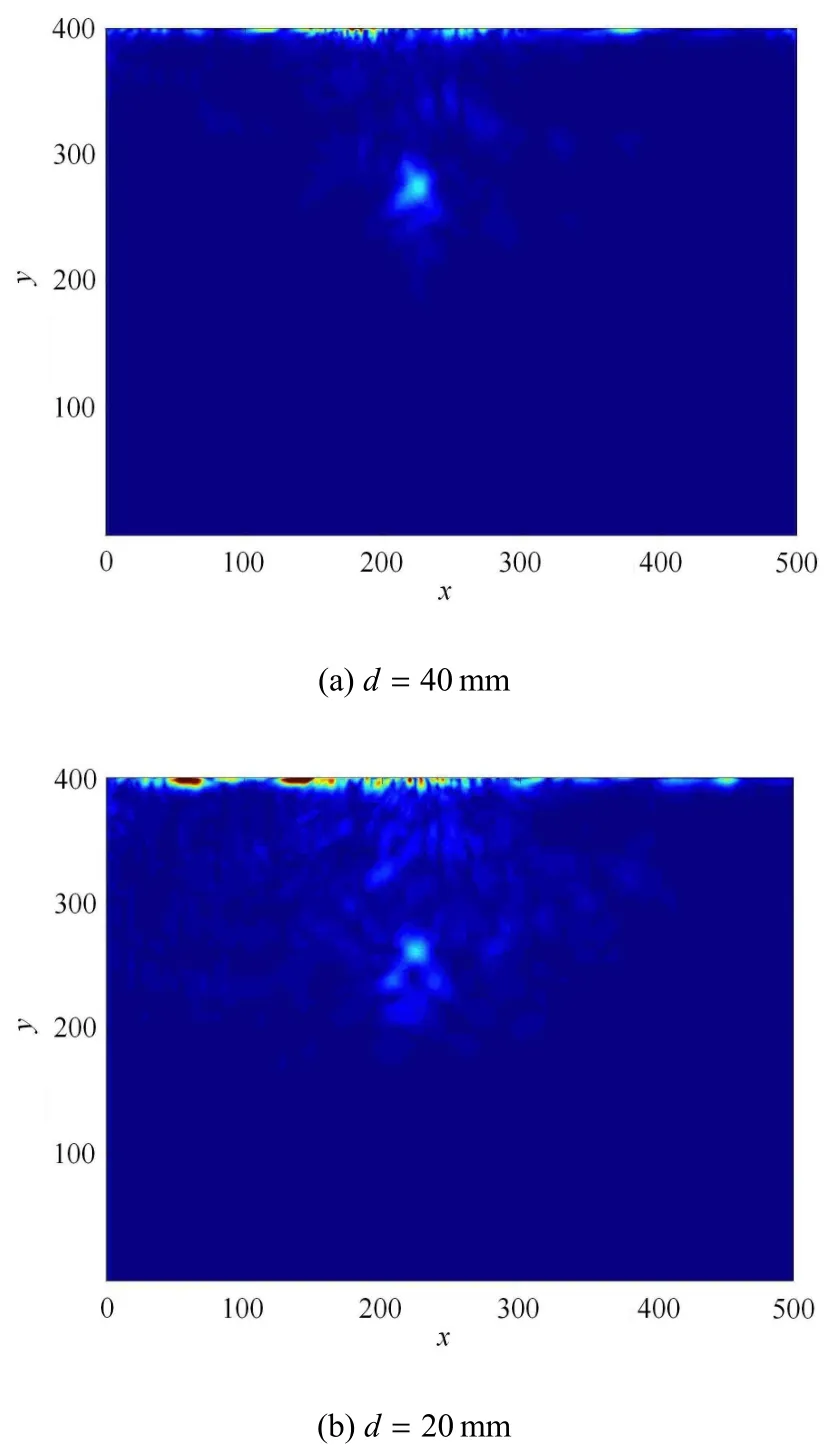
图6 不同损伤尺寸成像结果Fig.6 Damage imaging of di ff erentdiameters

4 结论

本文基于细观混凝土模型，结合时间逆转成像法进行损伤检测；通过正向检测和逆时成像两个过程完成损伤回波信号的提取和时反加载.时反加载在建立的与细观模型相同尺寸的等效模型中进行，损伤回波信号在损伤处发生干涉叠加；通过提取时反过程波场数据，并进一步结合小波变换法提取信号主频率对应的能量幅值，最终对基于小波变换后的全场数据进行最大幅值出现时刻的识别并获取该时刻对应原始波场以及小波变换能量场，完成成像，成像结果清晰且成功匹配了损伤表面的几何位置.数值计算结果表明，时间逆转模型对复杂混凝土结构的损伤定位具有强的适用性，基于小波变换的单时刻成像法能够消除噪声干扰提高成像精度.本文采用依据真实试件的骨料级配曲线建立细观混凝土模型提高了研究的实际应用价值，提出的适用于复杂混凝土结构的损伤定位方法，对混凝土结构内部损伤检测的工程实践具有较强的指导及应用价值.

1万征，姚仰平，孟达.复杂加载下混凝土的弹塑性本构模型.力学学报，2016,48(5)：1159-1171(Wan Zheng,Yao Yangping,Meng Da.An elastoplastic constitutivemodel of concrete under complicated load.Chinese JournalofTheoreticaland Applied Mechanics,2016,48(5)：1159-1171（in Chinese))

2 Wittmann FH,Roelfstra PE.Simulation and analysis of composite structures.Materials Science and Engineering,1984,68(2)：239-248

3 Schlangen E,Van M ier JGM.Simple latticemodel for numerical simulation of fracture of concretematerials and structures.Materialsand Structures,1992,25(9)：534-542

4 W riggers P,Moftah SO.Mesoscalemodels for concrete：homogenization and damage behaviour.Finite Elements in Analysis and Design,2006,42(7)：623-636

5 Leite JPB,Slow ik V,Apel J.Computationalmodel ofmesoscopic structure of concrete for simulation of fracture processes.Comput-ersand Structures,2007,85(17/18)：1293-1303

6 Wang ZM,Kwan AKH,Chan HC.Mesoscopic study of concrete I：generation of random aggregate structure and finit elementmesh.Computers&Structures,1999,70(5)：533-544

7马怀发,陈厚群,黎保琨.混凝土试件细观结构的数值模拟.水利学报,2004,35(10)：27-35(Ma Huaifa,Chen Houqun,Li Baokun.Meso-structure numerical simulation of concrete specimens.JournalofHydraulic Engineering,2004,35(10)：27-35(in Chinese))

8杨华,李宗利,惠弘毅.基于随机骨料模型的混凝土弹性模量预测研究.长江科学院院报,2016,33(2)：100-105(Yang Hua,Li Zongli,HuiHongyi.Prediction ofelasticmodulusof concretebased on random aggregatemodel.JournalofYangtze River Scientifi Research Institute,2016,33(2)：100-105(in Chinese))

9 Leslie JR,CheesmanWJ.An ultrasonicmethod of studying deterioration and cracking in concrete structures.Journalofthe American Concrete Institute，1949,21(1)：17-36

10 Clayton D,Barker A,A lbright A,et al.Improved synthetic aperture focusing technique resultsof thick concrete specimens through frequency banding//Chimenti DE,Bond LJ.AIP Conference Proceedings.AIPPublishing,2016,1706(1)：020012

11 FendtKT,Mooshofer H,Rupitsch SJ,etal.Ultrasonic defect characterization in heavy rotor forgingsbymeansof the synthetic aperture focusing technique and optimizationmethods.IEEE Transactions on Ultrasonics,Ferroelectrics,and Frequency Control,2016,63(6)：874-885

12 BeniwalS,Ghosh D,GanguliA.Ultrasonic imaging of concreteusing scattered elastic wave modes.NDT&E International,2016,82(1)：26-35

13 Liu Z,Sun K,Song G,etal.Damage localization in alum inum plate w ith compact rectangularphased piezoelectric transducerarray.MechanicalSystemsand SignalProcessing,2016,70(1)：625-636

14 Vassholz M,Koberstein-Schwarz B,Ruhlandt A,etal.New X-ray tomography method based on the 3d Radon transform compatible w ith anisotropic sources.Physical Review Letters,2016,116(8)：088101-1

15李飞,余西龙,林鑫.基于TDLAS的层析成像技术TDLAT.力学学报,2014,46(1)：55-59(LiFei,Yu Xilong,Lin Xin.Parallel-beam tomography based on TDLAS.Chinese Journal ofTheoretical and Applied Mechanics,2014,46(1)：55-59(in Chinese))

16邱雷,袁慎芳,苏永振.基于Shannon复数小波和时间反转聚焦的复合材料结构多源冲击成像定位方法.航空学报,2010,31(12)：2417-2424(Qiu Lei,Yuan Shenfang.Multiple impactsource imaging and localization on composite structure based on shannon complex waveletand time reversal focusing.Acta Aeronautica EtAstronautica Sinica,2010,31(12)：2417-2424(in Chinese))

17王强,袁慎芳.主动Lamb波结构健康监测中信号增强与损伤成像方法.航空学报,2008,29(4)：1061-1067(Wang Qiang,Yuan Shenfang.Amplifying signal and imaging damagemethod for active lamb-wave structure health monitoring.Acta Aeronautica Et Astronautica Sinica，2008,29(4)：1061-1067(in Chinese))

18王强,袁慎芳.无参考主动Lamb波结构损伤时反成像监测方法.航空学报,2010,31(1)：178-183(Wang Qiang,Yuan Shenfang.No baseline time reversal imagingmethod for active lamb wave structuraldamagemonitoring.Acta Aeronautica Et Astronautica Sinica,2010,31(1)：178-183(in Chinese))

19 Zhu R,Huang GL,Yuan FG.Fastdamage imaging using the timereversal technique in the frequency-wavenumber domain.Smart Materialsand Structures,2013,22(7)：075028

20 He J,Harb MS,Yuan FG.Non-contact ultrasonic technique for Lambwave characterization in composite plates.Ultrasonics,2016,64(1)：162-169

21 Chen C,Yuan FG.Impact source identificatio in finit isotropic platesusing a time-reversalmethod：theoreticalstudy.SmartMaterialsand Structures,2010,19(10)：105028

22 Fink M,Cassereau D,Derode A,et al.Time-reversed acoustics.Reportson Progress in Physics,2000,63(12)：1933

23 Saenger EH.Time reverse characterization of sources in heterogeneousmedia.NDT&E International,2011,44(8)：751-759

24 Kocur GK,Saenger EH.Deconvolution of acoustic em issions for source localization using time reversemodeling.Journal ofSound and Vibration,2017,387(1)：66-78

25 Saenger EH,Kocur GK,Jud R,et al.Application of time reverse modeling on ultrasonic non-destructive testing of concrete.Applied MathematicalModelling,2011,35(2)：807-816

26 SaengerEH.Numericalmethods to determinee ff ectiveelastic properties.International Journal ofEngineering Science,2008,46(6)：598-605

27 Saenger EH,Shapiro SA.E ff ective velocities in fracturedmedia：a numerical study using the rotated staggered finite-d ff erence grid.Geophysical Prospecting,2002,50(2)：183-194

28 Steiner B,Saenger EH,Schmalholz SM.Time reversemodeling of low-frequency m icrotremors：application to hydrocarbon reservoir localization.GeophysicalResearch Letters,2008,35(3)：L03307

29 Kocur GK,Saenger EH,Grosse CU,et al.Time reversemodeling of acoustic em issions in a reinforced concrete beam.Ultrasonics,2016,65(1)：96-104

30蔡伟,陈文.复杂介质中任意阶频率依赖耗散声波的分数阶导数模型.力学学报,2016,48(6)：1265-1280(CaiWei,ChenWen.Fractuionalderivativemodeling of frequency-dependentdissipative mechanism forwave propagation in complexmedia.Chinese JournalofTheoreticaland Applied Mechanics,2016,48(6)：1265-1280(in Chinese))

31唐春安,朱万成.混凝土损伤与断裂一数值试验.北京：科学出版社,2003(Tang Chunan,ZhuWancheng.A Numerical Experiment of Concrete Damage and Fracture.Beijing：Science Press,2003(in Chinese))

32 Doucet A,Freitas DN,Gordon N.An introduction to sequential MonteCarlomethods.Statistics forEngineering&Information Science,2001,18(1)：3-14

33 Walraven JC,Reinhardt HW.Theory and experiments on themechanical behaviour of cracks in plain and reinforced concrete subjected to shear loading.HERON,1981,26(1A)：1-68

34 Liu Y,Li Z,ZhangW.Crack detection of fibr reinforced composite beams based on continuouswavelet transform.Nondestructive Testing&Evaluation,2010,25(25)：25-44

DAMAGEDETECTIONOFMESO-SCALECONCRETE STRUCTURESBASED ON TIME REVERSALMETHOD1)

Zhao Guoqi2)Qiu Yaping Luo Ying Feng Kan
(Faculty ofCivil Engineering and MechanicsofJiangsu University，Zhenjiang 212013，Jiangsu，China)

A specifi time reversal imaging method is proposed in this article to detect defects in concrete structures.In order to detect the damage that the scale is the same as the aggregate,ameso-scale concretemodel is introduced in thisarticle.As the concrete isa compositematerial composed by cement,aggregate,waterand concrete admixtures,the Monte Carlo random modeland the aggregate grading curve of real concrete samples are introduced for designing this finit elementmodel.Then,thedamagedmodelwasanalyzed by employing aself-adapted time reversedmodel to achieve the ultrasonicwave fiel simulation.This imagingmethod contains two steps：the firs is the forward detection.A series of reflecte echo signalsw ith damage information are obtained in this section.These

signals can be reversed in Matlab to serve as the incident signals in the next Time Reversal process;the second step is to image the damage location via interfering thewave-frontsactuated by di ff erent transducers to illustrate the peaks ofwaveform amplitudes.By determ ining the interfering wave peak time,obtaining the originalwave fiel of thatmoment,we can form ing the wavelet transform energy field and then complete the damage imaging of the concretemodelw ith defect.In the time reversalprocess,we introduced theequivalentelastic parametersas the same geometric dimension of the originalmesosacleconcretemodel to locate thedamagee ff ectively.Comparedw ith theoriginalwave field theenergy fiel modifie by wavelet transform can lower thee ff ectof theenvironmentalnoise.Finally,we discussed theequivalentelastic parameters and the damage sizes to verify the robustnessof thismethod which isapplicable inmonitoring and evaluating the damage in concrete structures.

concrete structure,meso-scalemodel,time reversalmethod,ultrasonic detection,damage imaging

TU317+.8,O347.4+1

A

10.6052/0459-1879-17-007

2017-01-04收稿，2017-03-23录用,2017-03-24网络版发表.

1)国家自然科学重点国际合作项目(11520101001)、江苏大学高级人才启动基金(5501480007)资助.

2)赵国旗，副教授，主要研究方向：结构健康监测与检测新技术研究及应用.E-mail：flagzhao@163.co

赵国旗,仇亚萍,骆英,冯侃.基于细观混凝土模型的时间逆转损伤成像方法.力学学报,2017,49(4)：953-960

Zhao Guoqi,Qiu Yaping,Luo Ying,Feng Kan.Damage detection ofmeso-scale concrete structures based on time reversalmethod.Chinese JournalofTheoreticaland Applied Mechanics,2017,49(4)：953-960