弹塑性微凸体侧向接触相互作用能耗1)

高志强傅卫平王雯康维超吴洁蓓刘雁鹏

(西安理工大学机械与精密仪器工程学院，西安710048)

固体力学

弹塑性微凸体侧向接触相互作用能耗1)

高志强傅卫平2)王雯康维超吴洁蓓刘雁鹏

(西安理工大学机械与精密仪器工程学院，西安710048)

传统的结合面研究多基于光滑刚性平面与等效粗糙表面接触假设，忽略了结合面上微凸体侧向接触及相邻微凸体之间的相互作用，这导致理论模型与实际结合面存在较大出入.针对承受法向静、动态力的机械结合面，从微观上研究了微凸体侧向接触及相互作用的接触能耗.将法向静、动态力分解为法向分力和切向分力，获取弹性/弹塑性/塑性阶段考虑微凸体侧接触及相互作用的加、卸载法向分力--变形和切向分力--位移的关系.通过力的合成定理，从而获取加、卸载法向合力与总变形之间的关系，由于法向分力产生的塑性变形及切向分力产生的摩擦，导致加载、卸载法向合力--总变形曲线存在迟滞回线.通过对一个加、卸载周期内的法向合力--总变形曲线积分，获得一个周期的微凸体接触能耗，包括应变能耗及摩擦能耗.仿真分析表明：微凸体在3个阶段的能耗均随变形的增大而非线性增大.微凸体侧向接触角度越大，能耗越大，且在弹性阶段最为明显.在弹性阶段，仅存在侧向的摩擦能耗，故结合面在低载荷作用下必须采用双粗糙表面假设.在塑性阶段，由于微凸体接触能耗为应变能耗，且接触角对其能耗影响甚微，故结合面在大载荷作用下可采用单平面假设对其进行研究.相对于KE和Etsion模型，本文提出的模型与Bartier的实验结果更吻合.

结合面，微凸体，侧向接触，相互作用，能耗

引言

机械结构中存在着大量的机械结合面，可将其分为固定结合面与移动结合面，为了研究法向静、动力作用下的固定结合面，本文针对结合面中微凸体在弹性、弹塑性、塑性阶段侧向接触及相邻微凸体相互作用的能耗进行了研究.国内外许多专家学者也对结合面中微凸体接触问题进行了研究，并做了大量工作[112].如早期的Hertz弹性球体接触模型[13]、GW模型[14]，这些模型仅针对弹性微凸体进行了研究，而忽略了微凸体在弹塑性及塑性阶段的接触情况.Abbott和Firestone[15]考虑到GW模型的局限性，在GW模型基础上进一步研究了微凸体在塑性变形阶段的接触情况；但该模型不仅忽略了微凸体塑性变形体积不变原则，而且未考虑弹塑性阶段的接触情况.Chang等[16]基于微凸体塑性变形体积不变原则，建立了微凸体弹性、弹塑性、塑性3个阶段的微凸体接触模型(CEB模型)，该模型的力--位移曲线在微凸体发生塑性屈服的临界点处出现了不连续现象.Zhao等在文献[6]的基础上采用数学拟合的方法对CEB模型进行了改进，从而得到连续的力与位移曲线关系(ZMC模型)[17],并在该模型基础上建立了微凸体相互作用的扩展ZMC模型[18].田小龙等[19]利用ZMC相互作用模型，在KE模型的基础上对考虑微凸体相互作用的结合面做了进一步的研究.但上述模型均基于光滑刚性平面与等效粗糙表面的接触假设，不仅忽略了结合面中微凸体错位接触时的微凸体侧向接触情况，而且都是仅考虑加载时的接触模型，未考虑卸载时的情况.Sepehri等[20]研究了弹性阶段微凸体侧向接触且考虑微凸体相互作用的结合面接触模型，但该模型仅考虑微凸体在弹性阶段的情况，忽略了微凸体的弹塑性变形及塑性变形，且未考虑卸载时的情况.Gorbatikh等[21]研究了两粗糙表面在法向静力作用下相互接触，然后施加切向激振力时的微凸体切向能耗问题；但该模型仅考虑了微凸体发生弹性变形时的切向耗能情况.

针对上述模型存在的问题及不足，本文建立了微凸体侧向接触并考虑相邻微凸体之间相互作用时，在弹性/弹塑性/塑性阶段一个加、卸载周期内的能耗模型，其中包括侧向摩擦能耗及微凸体的应变能耗.首先，根据力的分解原理及ZMC相互作用模型，构建微凸体侧向接触及相互作用力学模型.其次，基于Hertz理论、KE模型，Etsion模型、Cattaneo-M indlin模型及ZMC相互作用模型等建立一对微凸体侧向接触加、卸载时，在弹性、弹塑性、塑性阶段的法向分力与变形之间的关系和切向分力与位移之间的关系.最后，根据力的合成原理，求得加、卸载时法向合力与总变形之间的关系.由于微凸体侧向接触时存在塑性变形和摩擦，故微凸体卸载时力--位移曲线滞后于加载时的力--位移曲线，存在迟滞现象，其加、卸载曲线包围的面积表示为一个振动加、卸载周期的能耗，通过积分求得弹性、弹塑性、塑性阶段微凸体接触能耗.分析微凸体总能耗与变形以及与接触角度之间的关系，为后续结合面的接触阻尼计算提供参考.

1 微凸体接触受力分析

1.1 微凸体侧向接触受力分析

两粗糙表面在法向静力Fs作用下相互接触，在此基础上施加法向正弦激振力Fd=Fmsin(ωt)，其合力为F=Fs+Fd.两粗糙表面接触时，结合面上微凸体接触方式多为侧向接触，正向接触为侧向接触的特殊情况(即接触角度为0时的侧向接触)，显然将微凸体接触假设为微凸体与光滑刚性平面接触的模型不能反映真实粗糙表面的接触情况.

取其中一对侧向接触的微凸体，对其进行受力分析，如图1所示.本文假设所取微凸体为球形微凸体，且微凸体同时参与侧向接触的数量不超过2个；在粗糙表面结合面上施加的力为均布载荷,微凸体接触过程中基体不发生变形.

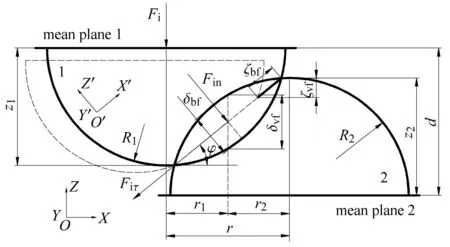
图1 微凸体侧向接触受力分析Fig.1 The forceanalysisof lateralcontact

由于假设结合面承受均布载荷，则结合面上的总力等于所有微凸体承受的力之和

式中，Fi为微凸体上承受的力，Fi=Fis+Fid=Fis+Fimsin(ωt)，Fis为微凸体上承受的静态力，Fid为微凸体上承受的激振力，Fim为微凸体上激振力幅值，ω为角频率，t为时间.

将结合面垂直方向设为Z方向，即结合面法向.结合面平行方向设为X方向，即结合面切向.垂直于XOZ平面方向为Y方向，建立OXYZ笛卡尔坐标系.将微凸体公切面垂直方向定为Z′方向，沿切平面方向为X′方向，垂直于X′O′Z′平面方向为Y′方向，建立O′X′Y′Z′笛卡尔坐标系.在结合面中取一对侧向接触的微凸体，其半径分别为R1和R2，两半径之和为Rs，微凸体等效曲率半径为R=(1/R1+1/R2)-1.微凸体接触角为φ.两微凸体球心之间的距离为r=r1+r2，r1和r2分别表示微凸体1和2球心与微凸体接触面的圆心之间的距离，且存在r=Rstanφ，z1和z2分别为两微凸体高度.

一对微凸体侧向接触时，作用在其上的法向力Fi可分解为Z′方向的法向分力Fin和X′方向的切向分力Fiτ.法向分力Fin在Z′方向上产生的变形为δbf，在Z方向上的变形为δvf，且存在δvf=δbfcosφ；切向分力Fiτ在X′方向上产生的位移为ζbf，在Z方向上产生的位移为ζvf，且存在ζvf=ζbfsinφ.

根据文献[20]建立的双粗糙表面模型可得微凸体侧接触产生的Z′方向的无量纲变形δ∗bf为

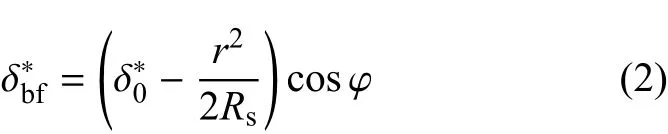
1.2 微凸体相互作用受力

Zhao等[18]假设当光滑刚性平面与等效粗糙表面接触时，微观上各微凸体底部存在与之对应的基底面积，当载荷增大时，基底面积随之增大，如图2所示.

图2 微凸体相互作用受力分析Fig.2 The force analysisof interaction between asperities

根据圣维南定理和勒夫方程，Zhao[18]给出了相邻微凸体相互作用时产生的局部变形与微凸体上承受的力以及材料属性之间的关系.由于相邻微凸体相互作用产生的Z′方向的无量纲局部总变形为

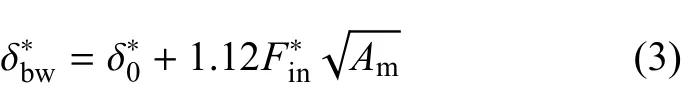
但Zhao给出的模型基于光滑刚性平面与微凸体的正向接触，忽略了两微凸体侧向接触时，由于接触角度导致的局部变形的偏移.

综合考虑微凸体侧接触及相互作用的影响.引入侧向接触时接触角度及侧向作用力的影响，并考虑相邻微凸体相互作用导致的局部变形，可得Z′方向的总变形为由于文中参数较多，故定义各变量上、下标来区分各变量，定义规则如下：

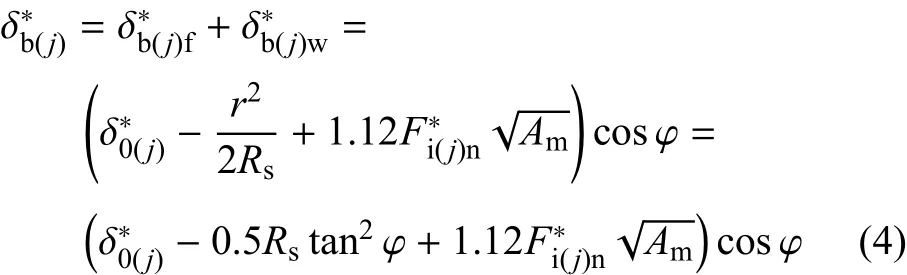
(1)文中所有上标“∗”均默认为无量纲；

(2)下标i表示微凸体；

(3)下标j=e,ep,p分别表示弹性、弹塑性、塑性阶段；

(4)下标b表示在O′X′Y′Z′坐标系内的倾斜方向；

(5)下标f表示由于力直接作用于微凸体上产生的变形或位移；

(6)下标w表示由于相邻微凸体之间相互作用产生的局部变形或局部位移；

(7)下标s表示静力，下标d表示激振力；

(8)力的下标n表示法向分力，下标τ表示切向分力；

(9)下标m表示最大值或幅值.

2 微凸体侧向接触加、卸载时法向分力的相互作用模型

Kogut和Etsion[22]将结合面上微凸体的变形分为4个阶段，即弹性阶段、弹塑性I阶段、弹塑性II阶段、塑性阶段，Etsion等[23]在此基础上又对其进行了改进，将微凸体弹塑性I、II阶段合成为一个弹塑性阶段.本文将微凸体变形分为3个阶段进行研究.当微凸体变形与相邻微凸体相互作用产生的局部变形之和在区间和动态法向分时，微凸体发生弹性变形；在区间时，微凸体发生弹塑性变形；在区间时，微凸体发生完全塑性变形.

微凸体在法向静力与法向激振力共同作用下侧向接触时，微凸体在Z′方向上承受着静态法向分力Fisn和动态法向分力Fidn，Fidn=Fidn msin(ωt)，当时间t在区间-π/(2ω)≤t≤π/(2ω)时，微凸体承受加载的法向分力，当时间t在区间π/(2ω)≤t≤3π/(2ω)时，微凸体承受着卸载的法向分力.加载时，微凸体随着动态法向分力的增大，变形逐步增大，当动态法向分力达到最大值时开始逐渐卸载.当微凸体变形超过发生塑性变形的临界值时(即微凸体内部发生不可恢复的塑性变形，卸载完成后，微凸体仍然有部分未恢复的变形，将其定义为残余变形[23-28].

根据Etsion模型[23]可得微凸体侧向接触时，最大法向分力与Z′方向残余变形的关系和卸载时的法向分力与变形之间的关系

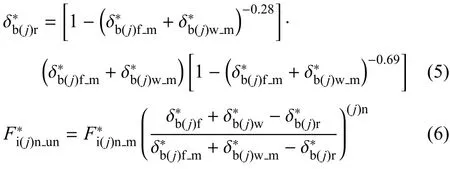
2.1 弹性阶段

(1)弹性加载阶段

Hertz最早对弹性球体接触进行了研究，Hertz接触理论是当前弹性力学的基础.为了考虑相邻微凸体在弹性阶段对局部变形的影响，将上述微凸体相互作用产生的局部变形代入到经典Hertz接触理论中，可得弹性阶段考虑微凸体相互作用及侧向接触的加载时的法向分力与变形之间的关系

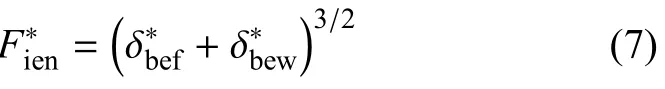
(2)弹性卸载阶段

根据KE模型[22]可得，弹性阶段无量纲变形的最大值等于1，将其代入式(5)可得残余变形为0，故由式(4)可得，弹性阶段卸载时的法向分力为

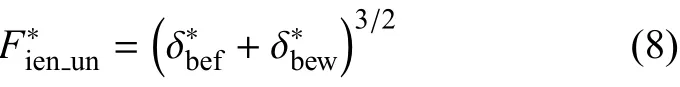
可见式(7)等于式(8)，故微凸体弹性阶段加载时的法向分力--变形曲线与卸载时的曲线相重合.

2.2 弹塑性阶段

(1)弹塑性加载阶段

根据Etsion模型[23]可得，弹塑性阶段加载时的法向分力与变形的关系为

(2)弹塑性卸载阶段

由于在弹塑性阶段，微凸体内部会发生不可恢复的部分塑性变形，故存在残余变形，弹塑性阶段的残余变形可由式(5)获得.将获取的残余变形代入式(6)可得弹塑性阶段卸载时的法向分力与变形之间的关系为

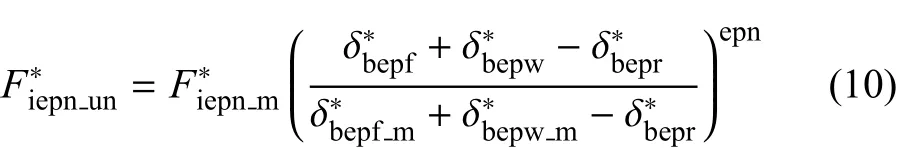
2.3 塑性阶段

(1)塑性加载阶段

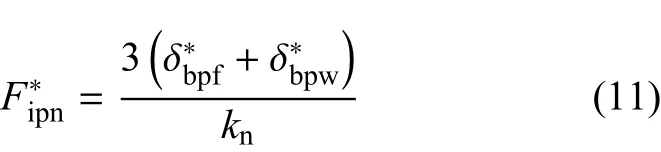
(2)塑性卸载阶段

由于微凸体在塑性阶段，微凸体内部会发生不可恢复的残余变形，由式(5)可得塑性阶段的残余变形，将其代入式(6)，从而获得微凸体塑性阶段卸载时的法向分力与变形之间的关系为

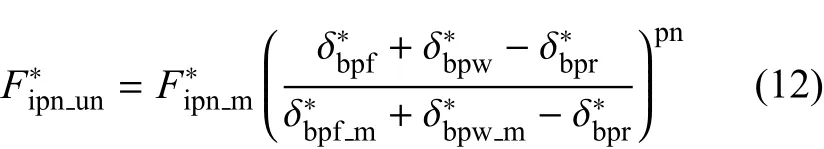
3 微凸体侧向接触加、卸载时切向分力的相互作用模型

微凸体在静、动态合力Fi下侧向接触时，可将其分解为Z′方向上的法向分力Fin和X′方向上Fiτ.法向分力会导致微凸体的变形，而切向分力会在微凸体侧向产生摩擦，并伴随着相邻微凸体之间的相互作用.本节对切向加卸载分力在弹性、弹塑性、塑性阶段产生的位移及相邻微凸体产生的局部位移之间的关系进行分析.

微凸体上的切向分力Fiτ同样包括静态切向分力Fisτ和动态切向分力Fidτ，Fidτ=Fidτmsin(ωt)，当时间t在区间-π/(2ω)≤t≤π/(2ω)时，微凸体承受加载的切向分力，当时间t在区间π/(2ω)≤t≤3π/(2ω)时，微凸体承受着卸载的切向分力.加载时，切向分力逐渐增大，当切向分力大于最大静摩擦力时，微凸体侧向发生滑移.当切向分力达到最大时逐渐开始卸载.由于加卸载过程中微凸体侧向存在摩擦，导致微凸体加载时的切向分力--位移曲线与卸载时的切向分力--位移曲线不重合，存在迟滞现象.

根据Masing迟滞准则[28]，可得卸载时的切向分力与位移之间的关系为

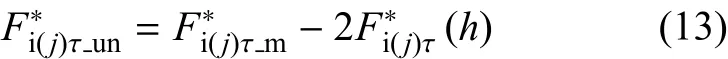
3.1 弹性阶段

微凸体在法向分力作用下发生变形，根据KE模型[22]可得，当微凸体无量纲变形在区间时，微凸体发生弹性变形.

(1)弹性加载阶段

Cattaneo[24]和M indlin[25]揭示了两接触弹性球体在法向和切向力共同作用下的行为，给出了切向力与切向位移之间的非线性关系，且接触面为环形区域.当切向力小于最大静摩擦力时，在微凸体接触环形区内部发生黏着，仅在外环边缘产生微观滑移；随着切向载荷不断增大，滑移区也不断增大，当切向力大于最大静摩擦力时，黏着区被滑移区占据，整个接触区域变为滑移区，两球体之间发生宏观滑动.Johnson[28]通过实验验证了Cattaneo--M indlin理论的正确性.

根据Cattaneo--M indlin模型[2425]可得微凸体在弹性阶段的切向分力与位移之间的关系，当时，微凸体侧向发生黏着；当时，微凸体侧向发生滑移.即

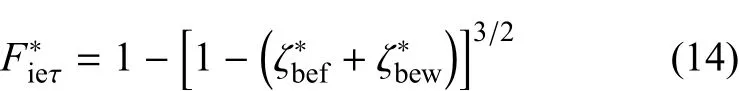
(2)弹性卸载阶段

3.2 弹塑性阶段

由于Cattaneo-M indlin理论仅适用于微凸体在法向力作用下发生弹性变形的情况，该模型不适用于弹塑性及塑性变形情况.根据Eriten等[29]给出的改进模型，通过改变微凸体之间的摩擦因数，仍基于Cattaneo-M indlin模型，可求得微凸体发生弹塑性变形时切向分力与位移之间的关系.

根据KE摩擦因数模型[30]和BKE模型[27]分别可得微凸体无量纲变形与摩擦因数之间的关系.

KE摩擦因数模型

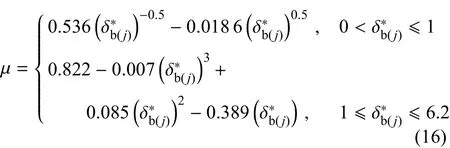
BKE模型

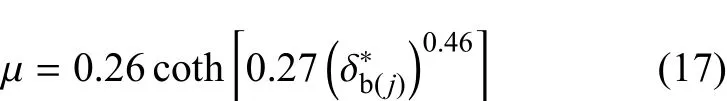
对KE摩擦因数模型、BKE模型及Ovcharenko等[31]获得的实验数据进行仿真可得摩擦因数与变形之间的关系，如图3所示.

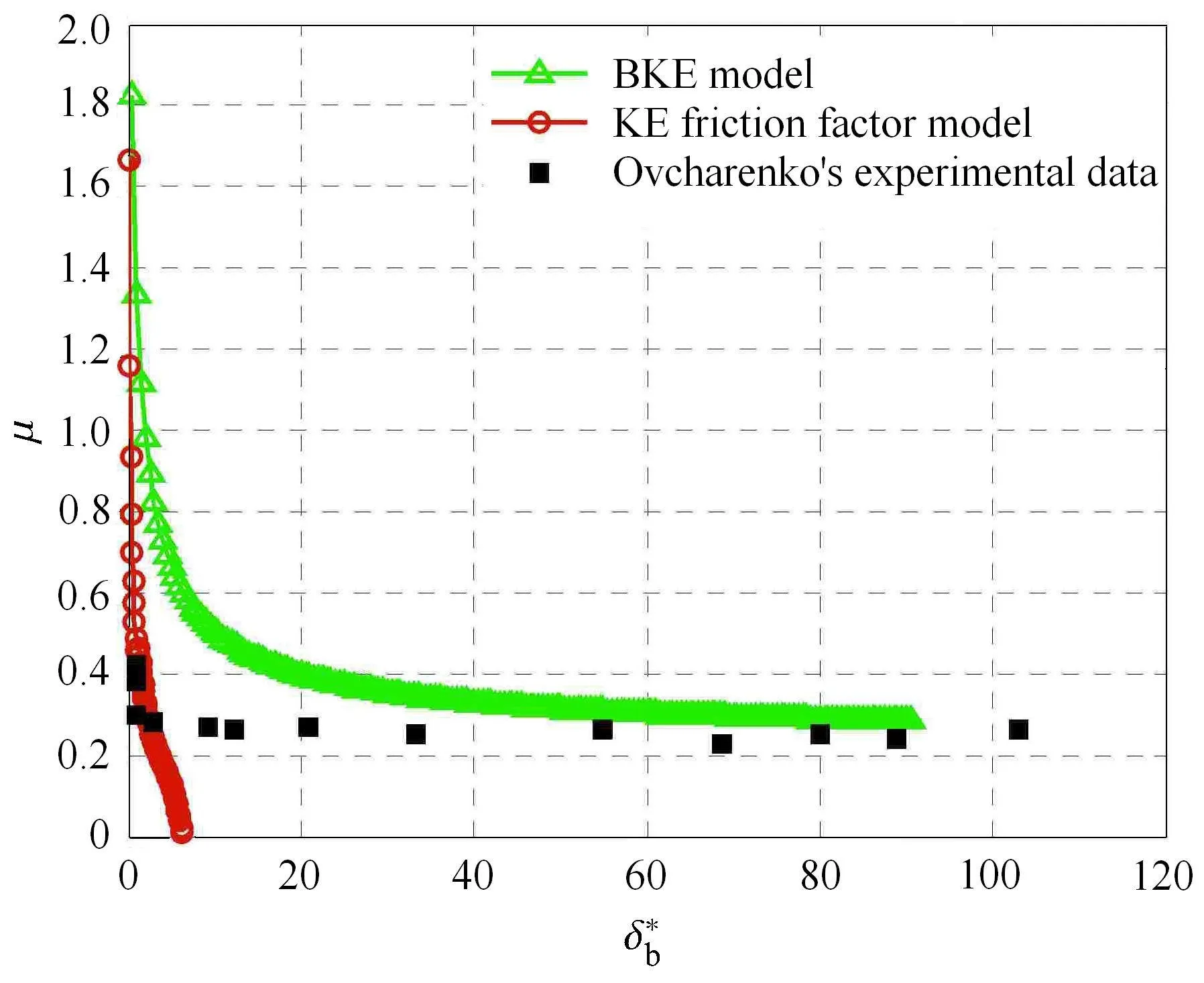
图3 变形与摩擦因数之间的关系Fig.3 The relationship between deformation and friction factor

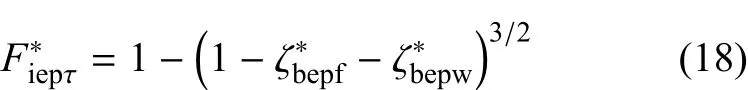
(2)弹塑性卸载阶段

根据式(13)可得

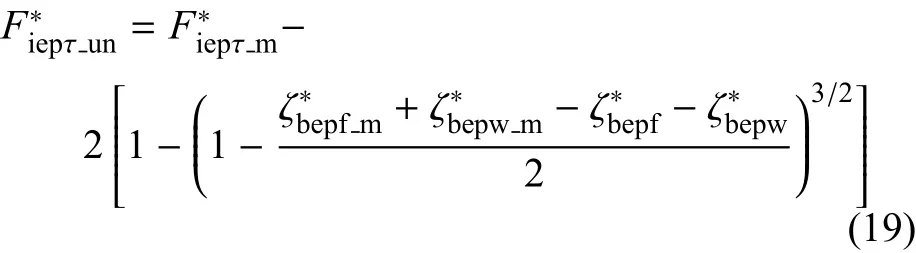
3.3 塑性阶段

(1)塑性加载阶段

Fujimoto等[32]通过理论和实验的方法建立了塑性阶段微凸体切向受力模型.根据此模型可得切向分力与位移之间的关系，当X′方向的切向位移时，微凸体侧向发生黏着，当切向位移时，微凸体侧向发生滑移.即

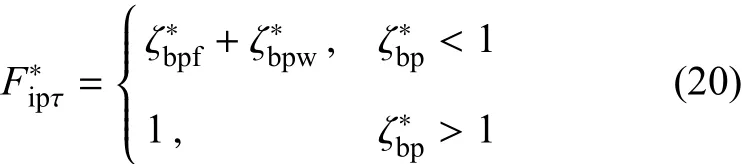
(2)塑性卸载阶段

根据式(11)可得

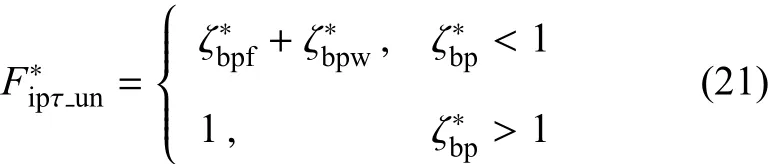
可见,塑性阶段卸载时的切向分力与位移之间的关系和加载时的切向分力与位移之间的关系相同，故微凸体在塑形阶段加载时的切向分力--位移曲线与卸载时的切向分力--位移曲线重合.

4 微凸体侧向接触加--卸载时法向合力相互作用模型

一对微凸体在Z方向的法向力Fi=Fis+Fid作用下侧向接触时，根据力的合成定理可得法向合力Fi与法向分力Fin、切向分力Fiτ之间的关系为

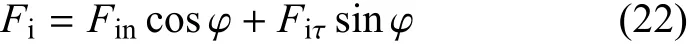
根据力的分解定理可得，法向分力Fin与法向合力Fi之间的关系为

根据力的分解定理可得，切向分力Fiτ与法向力Fi之间的关系为

文章第2,3部分分别给出了加、卸载法向分力与变形和加、卸载切向分力与位移之间在弹性、弹塑性、塑性阶段的关系.根据力的合成、分解定理求得弹性、弹塑性、塑性阶段在Z方向上加、卸载的法向合力与总变形之间的关系.

4.1 弹性阶段

(1)弹性加载阶段

根据式(22)、式(7)、式(14)可得

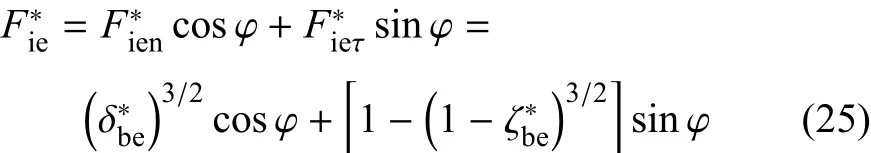
(2)弹性卸载阶段

根据式(22)、式(8)、式(15)可得

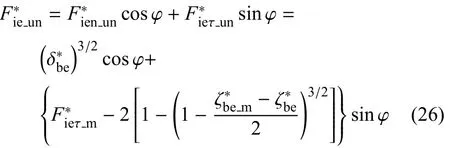
根据式(23)和式(24)可得

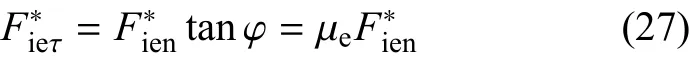
式(27)、式(7)、式(14)化简可得

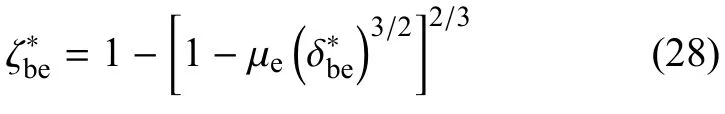
根据式(23)可得

4.2 弹塑性阶段

(1)弹塑性加载阶段

根据式(22)、式(9)、式(18)可得

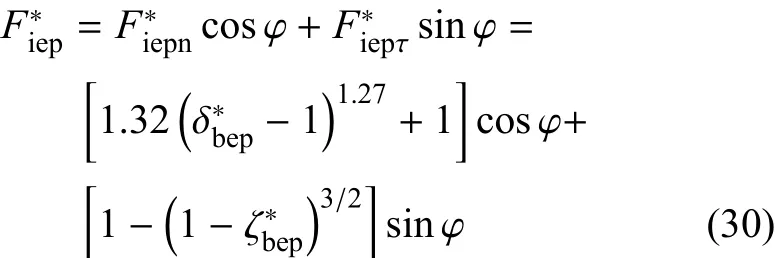
(2)弹塑性卸载阶段

根据式(22)、式(10)、式(19)可得

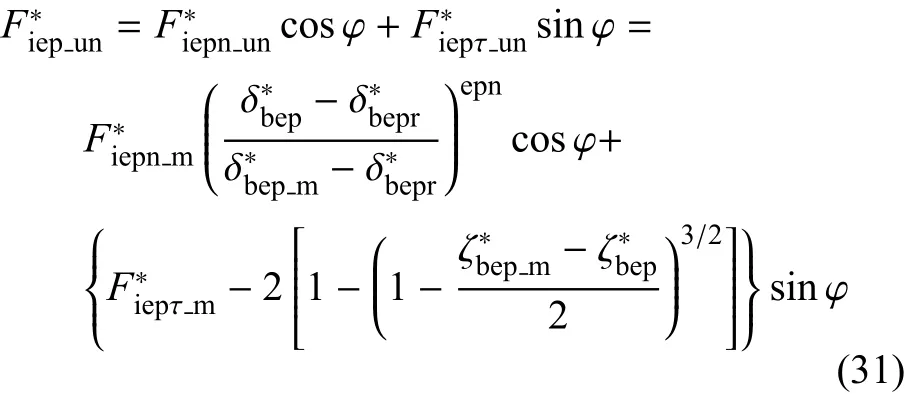
根据式(23)和式(24)，可得

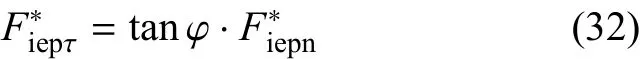
根据式(32)、式(9)和式(18)化简可得

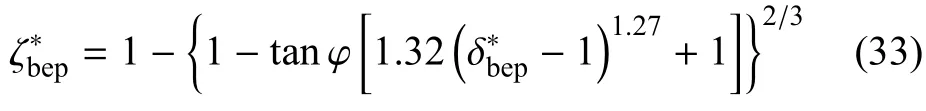
根据式(23)可得

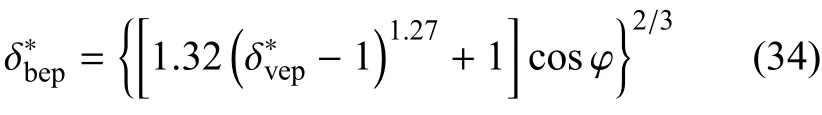
4.3 塑性阶段

(1)塑性加载阶段

根据式(22)、式(11)、式(20)可得

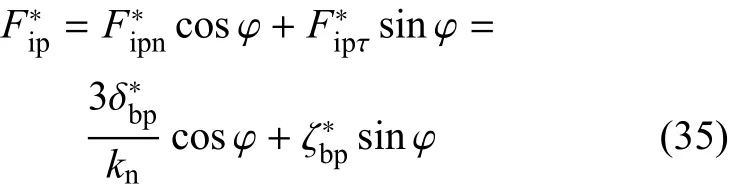
(2)塑性卸载阶段

根据式(22)、式(12)、式(21)可得

根据式(23)、式(24)可得

根据式(37)、式(11)、式(20)可得

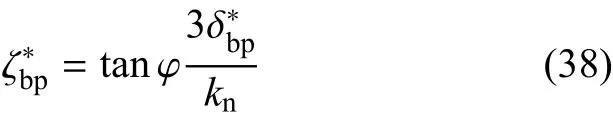
根据式(23)可得

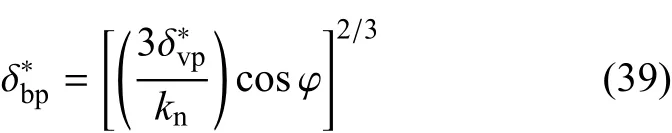
5 微凸体侧向接触相互作用法向能耗模型

微凸体在法向合力Fi作用下侧向接触时，在正弦激振力Fid=Fimsin(ωt)作用下，一个正弦周期-π/(2ω)≤t≤3π/(2ω)内，微凸体承受着加、卸载作用力.根据文中第2，3，4节的推导分析可得：由于微凸体塑性变形及微凸体侧向摩擦的存在，加、卸载法向合力--总变形曲线不重合，存在迟滞现象，其迟滞面积为一个加、卸载周期的能耗，通过对弹性、弹塑性、塑性阶段的加卸载合力--总变形曲线积分可得到3个阶段的法向能耗.

5.1 弹性阶段能耗

通过对弹性阶段加、卸载合力--总变形曲线进行积分可得一个周期的弹性阶段微凸体接触能耗

5.2 弹塑性阶段能耗

通过对弹塑性阶段加、卸载合力--总变形曲线进行积分可得一个周期的弹塑性阶段微凸体接触能耗

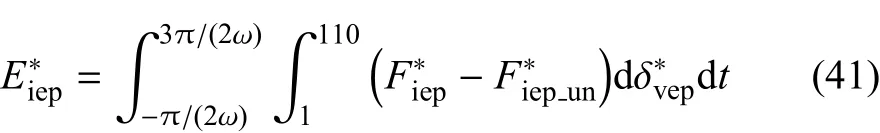
5.3 塑性阶段能耗

通过对塑性阶段加、卸载合力--总变形曲线进行积分可得一个周期的塑性阶段微凸体接触能耗

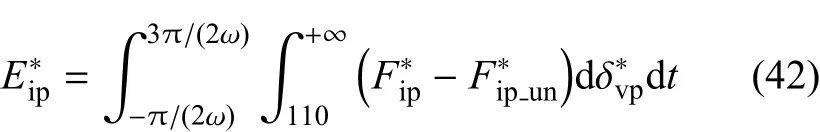
6 仿真分析

本文针对结合面中微凸体在静、动态力作用下侧向接触时的能耗进行了理论分析计算，根据文献[23]中所取的微凸体参数进行仿真，结合面上微凸体的材料及几何参数如下：弹性模量E=200GPa,硬度H=0.588GPa,剪切模量G=75.76GPa,泊松比ν=0.32,微凸体半径R=10mm.

6.1 弹性阶段能耗

根据式(40)对弹性阶段能耗进行仿真，如图4所示.

图4给出了微凸体在弹性阶段接触角φ分别为π/6,π/4,π/3时，考虑及不考虑微凸体相互作用的能耗对比仿真.当接触角不变时，考虑和不考虑微凸体相互作用的能耗均随着微凸体法向变形的增大而非线性增大.考虑微凸体相互作用的能耗大于不考虑微凸体相互作用的能耗，这是由于在加、卸载力作用下，微凸体相互作用会产生一部分位移，而加载力--局部位移曲线与卸载力--局部位移曲线不重合，导致能量耗损.当变形一定时，考虑微凸体相互作用与不考虑微凸体相互作用的能耗均随着接触角的增大而增大，且接触角对能耗的影响较为明显，能耗增长率的角度与微凸体接触角度基本一致.

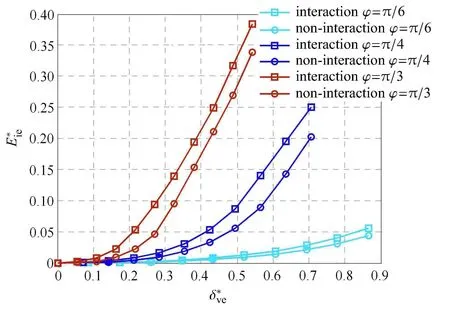
图4 弹性阶段微凸体变形与能耗之间的关系Fig.4 The relationship between deformation and energy dissipation in elastic stage

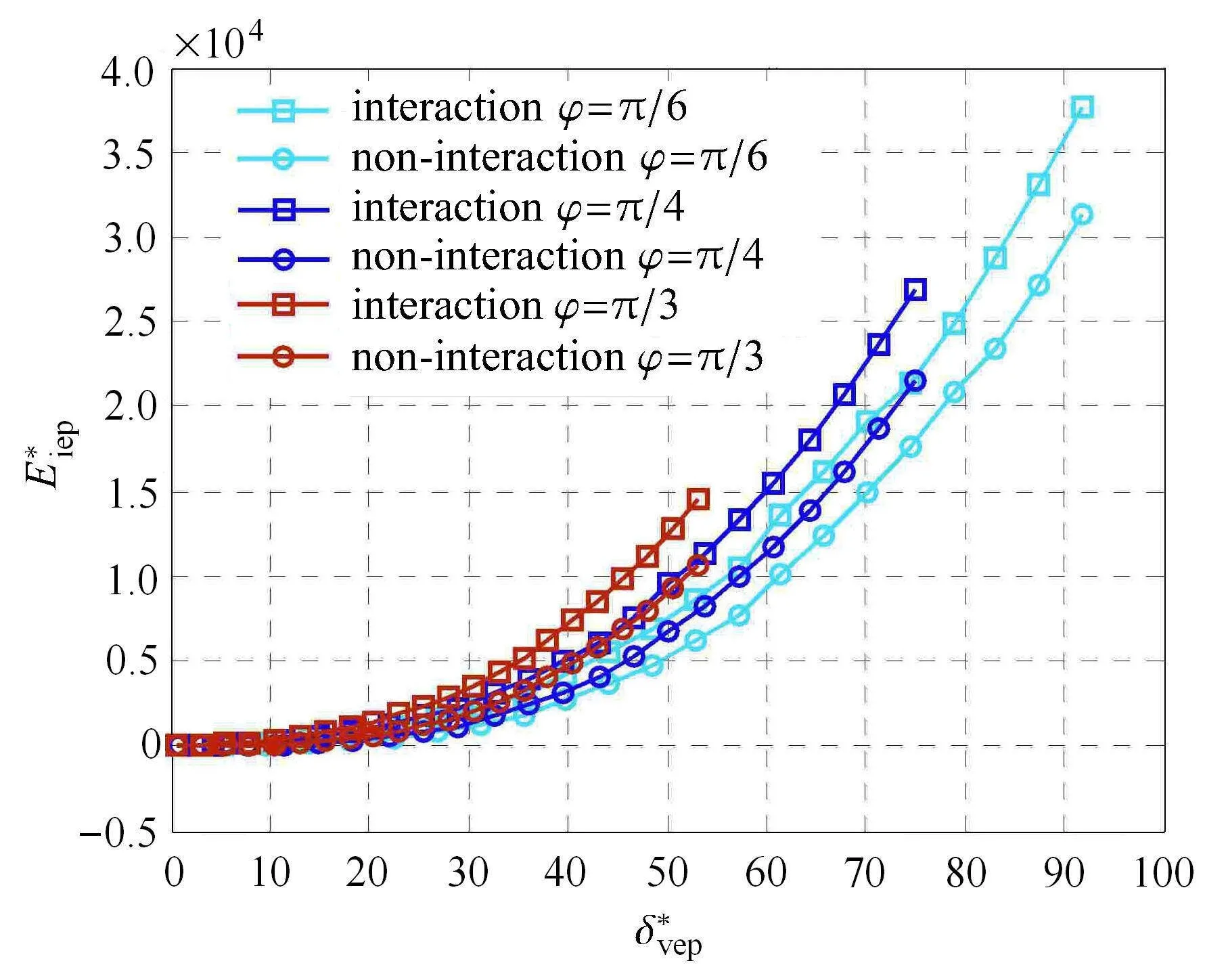
图5 弹塑性阶段微凸体变形与能耗之间的关系Fig.5 The relationship between deformation and energy dissipation in elastic-plastic stage

根据式(41)对弹塑性阶段能耗进行仿真，可得微凸体一个加、卸载周期内的弹塑性无量纲能耗与微凸体变形的关系，如图5所示.

图5同样给出了微凸体在弹塑性阶段接触角φ分别为π/6,π/4,π/3时，考虑和不考虑微凸体相互作用的能耗对比仿真.当接触角一定时，考虑和不考虑微凸体相互作用的能耗均随着变形的增大而非线性增大，且考虑微凸体相互作用的能耗大于不考虑微凸体相互作用的能耗.当变形一定时，微凸体接触角越大，能耗越大；但弹塑性阶段接触角对能耗的影响没有弹性阶段大.这是由于微凸体在弹塑性接触时发生了部分塑性变形.

根据式(42)对微凸体塑性阶段进行仿真，可得到微凸体塑性接触时一个加、卸载周期的能耗与变形的关系，如图6所示.

图6塑性阶段微凸体变形与能耗之间的关系Fig.6 The relationship between deformation and energy dissipation in plastic stage

图6 同样给出了微凸体在塑性阶段接触角φ分别为π/6,π/4,π/3时，考虑及不考虑微凸体相互作用的能耗对比仿真.当微凸体接触角一定时，考虑及不考虑微凸体接触能耗均随着变形的增大而非线性增大，且考虑微凸体相互作用的能耗大于不考虑微凸体相互作用能耗.当变形一定时，考虑及不考虑微凸体相互作用的能耗均随着微凸体接触角的增大而增大，且接触角对塑性阶段能耗的影响相对于弹性阶段更小.

图7取微凸体接触角φ=π/4且考虑微凸体相互作用时，给出了弹性、弹塑性、塑性3个阶段的接触能耗仿真.弹性阶段能耗最小，约为10-1～10，弹塑性阶段约为10-1～105，塑性阶段约为105～108，随着变形的增大，塑性阶段的接触能耗亦会随着增大.微凸体侧向接触及相互作用能耗在各阶段交点处为连续曲线.虽然塑性阶段产生的能耗较大，但在轻载荷作用下，弹性阶段能耗不能忽视.

图8给出了本文所提出的模型与KE模型、Etsion模型以及Bartier[33]实验的对比.虽然KE模型和Etsion模型仅对微凸体加、卸载进行了研究,但通过式(40)～式(42)可得一个加、卸载周期的能耗与变形之间的关系.Bartier试验材料为AISI 1035碳钢(即中国的35号钢)，其参数为：E=600GPa,H=0.882GPa,G=234.38GPa,v=0.28,R=0.5mm.其加、卸载数据详见文献[33]，采用指数函数对其进行拟合[34]，获得加、卸载力与变形关系表达式，通过积分获取一个加、卸载周期的能耗.根据仿真结果可以发现,本研究提出的能耗模型与实验的结果较吻合，而KE和Etsion模型能耗均小于Bartier的实验结果，这是由于它们忽略了微凸体侧向接触及相互作用的能量耗损.

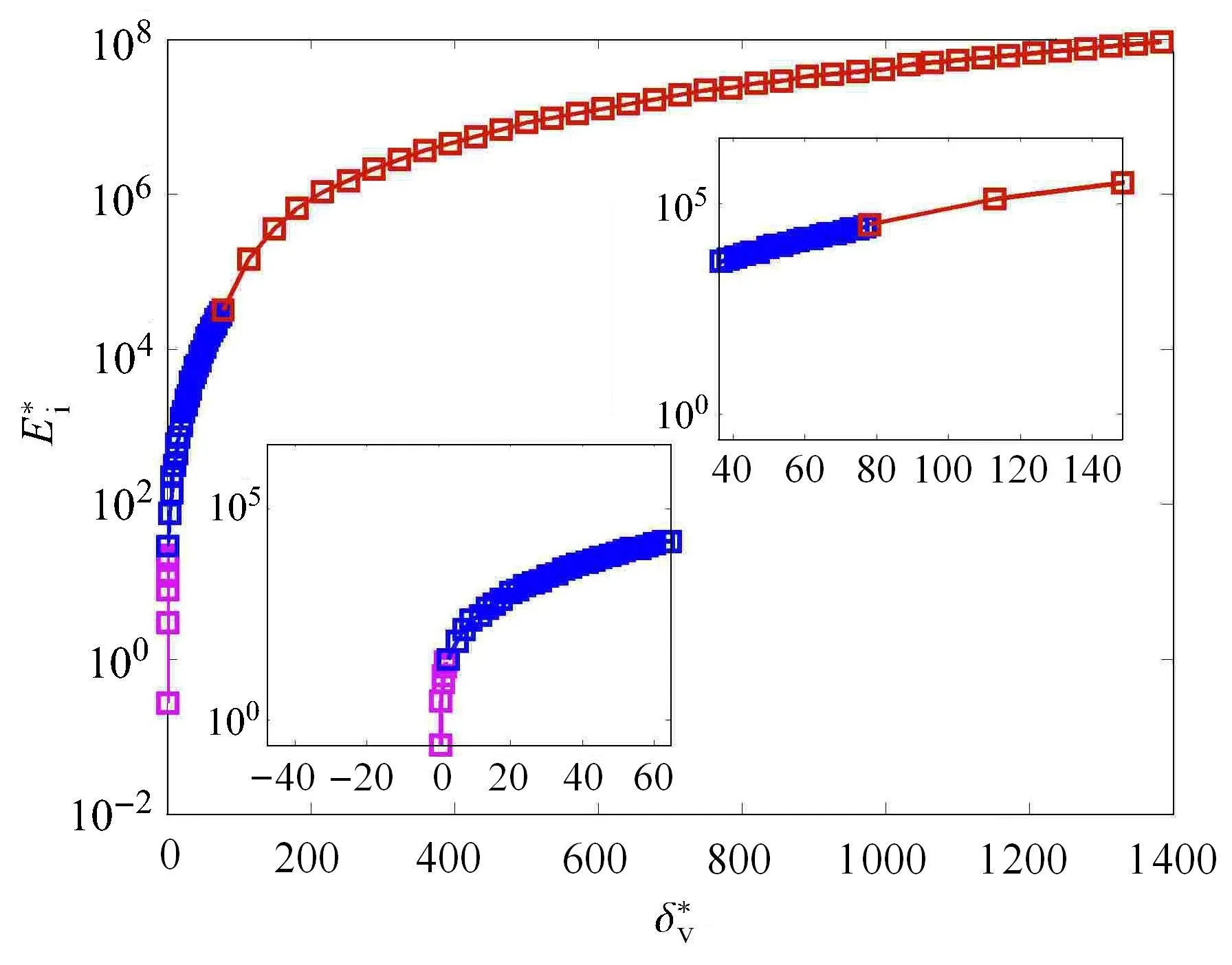
图7 三个阶段的接触能耗Fig.7 The contactenergy dissipation of three stages

图8 本文模型与KE模型、Etsion模型及Bartier的实验对比Fig.8 The comparison between the presentmodel,KEmodel,Etsion model,and Bartier’sexperiment

7 结论

为了解决结合面在法向静、动力下接触能耗问题，从微观上对微凸体侧向接触及相互作用的能耗进行了研究，可得如下结论：

(1)弹性阶段无塑性变形，故弹性阶段仅存在摩擦能耗，其摩擦能耗量级约为10-1～101.变形一定时，接触角对能耗影响较大，接触角度越大，能耗越大，且接触能耗增长率的角度约等于侧向接触角.由于弹性阶段无应变能耗，仅存在摩擦能耗，故在小载荷情况下，机械结合面模型必须采用双粗糙表面模型.

(2)弹塑性阶段能耗包括应变能耗和摩擦能耗，其量级约为10-1～105.当变形一定时，接触角越大，能耗越大，但接触角对能耗影响较小.

(3)塑性阶段能耗不存在摩擦能耗，仅包括应变能耗，其量级约为105～108.当变形一定时，接触度越大，能耗越大，但接触角对能耗的影响非常小.由于塑性阶段微凸体侧向无摩擦能耗，且接触角对能耗的影响甚微，故结合面在承受大载荷时可采用单平面假设.

(4)当3个阶段中接触角一定时，其能耗均随着变形的增大而非线性增大，且考虑微凸体侧接触及相互作用的能耗大于不考虑侧接触或不考虑相互作用的能耗.

(5)将本文中3个阶段能耗合成并与KE模型、Etsion模型和Bartier的实验结果进行对比分析可看出本文提出的能耗模型与Bartier的实验结果较为吻合.

后续将根据本文提出的微凸体侧向接触及相互作用模型，进一步考虑结合面的微凸体高度分布、接触角度分布等，从微观推广到宏观，对整个结合面的接触阻尼进行研究.

1 MaD,Liu C.Contact law and coe ffi cientof restitution in elastoplastic spheres.JournalofApplied Mechanics,2015，82(12)：1-9

2 You JM,Chen TN.Statisticalmodel for normaland tangential contactparametersof rough surfaces.JournalofMechanicalEngineering Science,2010,1(1)：1-15

3何联格,左正兴,向建华.考虑微凸体弹塑性过渡变形机制的结合面法向接触刚度分形模型.上海交通大学学报，2015，49(1)：116-121(He Liange,Zuo Zhengxing,Xiang Jianhua.Normal contactsti ff enss fractalmodelconseidering asperity elastic-plastic transitionaldeformationmechanism of joints.JournalofShanghai Jiao Tong University,2015,49(1)：116-121(in Chinese))

4 Ciavarella M.Rough contacts near full contactw ith a very simple asperitymodel.Tribology International,2016，93(12)：464-469

5王南山,张学良,兰国生等.临界接触参数连续的粗糙表面法向接触刚度弹塑性分形模型.振动与冲击,2014,33(9)：72-77(Wang Nanshan，Zhang Xueliang，Lan Guosheng,etal.Elastoplastic fractalmodel for normal contact sti ff ness of rough surfaces w ith continuous criticalcontactparameters.JournalofVibration and Shock,2014,33(9)：72-77(in Chinese))

6 Sun F,Giessen EVD,Nicola L.Dry frictional contact ofmetal asperities：A dislocation dynamicsanalysis.Acta Materialia,2016，109(13)：162-169

7 Sutyagin OV,Bolotov AN,Rachishkin AA.Computer simulation of the contactof rough surfaces.JournalofFriction andWear,2016，37(3)：198-203

8田红亮,余媛,陈甜敏等.考虑表面粗糙度和几何曲率的两球体接触问题.西安交通大学学报,2016,50(3)：1-7(Tian Hongliang,Yu yuan,Chen Tianm in,et al.Contact problem between two spheres considering surface roughness and geometrical curvature.Journal ofXi’an Jiaotong University,2016,50(3)：1-7(in Chinese))

9 Waghmare AK,Sahoo P.Friction analysis atelastic-plastic contact of rough surfaces using n-point asperity model.Journal ofEngineering Tribology,2016，23(3)：141-145

10 Yusof NFM,Ripin ZM.A technique to measure surface asperities plastic deformation and wear in rolling contact.Wear,2016；368(69)：496-504

11王雯,吴洁蓓,傅卫平等.机械结合面法向动态接触刚度理论模型与试验研究.机械工程学报,2016，52(13)：123-130(Wang Wen,Wu Jiebei,Fu Weiping,et al.Theoretical and experimental research on normaldynam ic contactsti ff nessofmachined jointsurfaces.Journal ofMechanical Engineering,2016，52(13)：123-130(in Chinese))

12 Kim M,Lee SM,Lee DW,etal.Tribologicale ff ectsof a rough surfacebearing using an average fl w analysisw ith a contactmodelof asperities.International JournalofPrecision Engineering&Manufacturing,2017，18(4)：521-534

13 Hertz H.On the contactof elastic solids.Journalfur die Reine und AndgewandteMathematik,1882，92(11)：156-171

14 Greenwood JA,Johnson KL,Matsubara E.A surface roughnessparameter in Hertz contact.Wear,1984,100(1-3)：47-57

15 Abbott E,Firestone F.Specifying surface quality：amethod based on accuratemeasurement and comparison.Journal ofMechanical Engineering,1933，55(23)：569-572

16 ChangWR,Etsion I,Bogy DB.Anelastic-plasticmodel for the contactof rough surfaces.JournalofTribology,1987，109(2)：257-263

17 Zhao Y,Maietta DM,Chang L.An asperitym icrocontactmodel incorporating the transition from elastic deformation to fully plastic fl w.JournalofTribology,2000，122(1)：86-93

18 Zhao Y,Chang L.A modelof asperity interactions in elastic-plastic contact of rough surfaces.Journal of Tribology,2001，123(4)：857-859

19田小龙,王雯,傅卫平等.考虑微凸体相互作用的机械结合面接触刚度模型.机械工程学报，2016，http：//www.cnki.net/kcms/detail/11.2187.TH.20161025.1547.040.htm l(Tian Xiaolong,Wang Wen,Fu Weiping,et al.The contact sti ff nessmodel of mechanical joint surfaces considering the asperity interactions.Journal of Mechanical Engineering,2016，http：//www.cnki.net/kcms/detail/11.2187.TH.20161025.1547.040.htm l(in Chinese))

20 SepehriA,Farhang K.On elastic interaction of nom inally fla rough surfaces.JournalofTribology,2008，130(1)：011-024

21 Gorbatikh L,PopovaM.Modeling of a lockingmechanism between two rough surfaces under cyclic loading.International Journal ofMechanical Sciences,2006，48(9)：1014-1020

22 Kogut L,Etsion I.Elastic-plastic contactanalysisof a sphere and a rigid flat Journalofapplied Mechanics,2002，69(5)：657-662

23 Etsion I,K ligerman Y,Kadin Y.Unloading of an elastic-plastic loaded spherical contact.International JournalofSolidsand Structures,2005，42(13)：3716-3729

24 Cattaneo C.Sul contatto di due corpielastici：distribuzione locale degli sforzi.I,II,III.Accademia nazionale dei Lincei,1938，27(21)：34-46

25 M indlin RD.Compliance of elastic bodies in contact.Journal of Applied Mechanics,1949，16(54)：259-268

26 J¨ager J.Uniaxial deformation of a random packing of particles.Archive ofApplied Mechanics,1999，69(3)：181-203

27 Brizmer V,K ligerman Y,Etsion I.Elastic-plastic spherical contact under combined normaland tangential loading in fullstick.Tribology Letters,2006；25(1)：61-70

28 Johnson KL.Contactmechanics.Journal of Tribology,1986，108(4)：464-476

29 Eriten M,Polycarpou AA,Bergman LA.Physics-based modeling for partialslip behavior of sphericalcontacts.International Journal ofSolids&Structures,2010，47(18-19)：2554-2567

30 Kogut L,Etsion I.A sem i-analytical solution for the sliding inception of a spherical contact.Journal of Tribology,2003，125(3)：499-513

31 Ovcharenko A,Halperin G,Etsion I.Experimental study of adhesive static friction in a spherical elastic-plastic contact.Journal of Tribology,2008，130(2)：021-032

32 Fujimoto T,Kagami J,Kawaguchi T,et al.M icro-displacement characteristics under tangential force.Wear,2000，241(2)：136-142

33 Bartier O,Hernot X,Mauvoisin G.Theoretical and experimental analysis of contact radius for spherical indentation.Mechanics of Materials,2010，42：640-656

34 FuWP,Huang YM,Zhang XL,etal.Experimental investigation of dynam ic normal characteristicsofmachined jointsurfaces.Journal ofVibration and Acoustics,2000，122(4)：393-398

THECONTACT ENERGY DISSIPATIONOF THE LATERAL AND INTERACTIONAL BETWEEN THE ELASTIC-PLASTIC ASPERITIES1)

Gao Zhiqiang FuWeiping2)WangWen KangWeichao Wu Jiebei Liu Yanpeng
(SchoolofMechanicaland Precision InstrumentEngineering，Xi’an University ofTechnology，Xi’an 710048，China)

The traditionalstudies aboutamechanical interfaceweremostly based on the assumption thata smooth rigid plane contactsw ith an equivalent rough surface,which ignored the lateral contactand interaction between asperities,so there has a serious error in those theoreticalmodels.Aimed at an interface bearing normal static and dynam ic force,the energy dissipation was studied from a m icro level,which considered the lateral contact and interaction between asperities.The normal force can be divided into a normal component of force and a tangential component of force.The relation between the normal component and the deformation,and the relation between the tangential component and the displacement can be gotten during loading/unloading in the elastic stage,elastic-plastic stage,and plastic stage,respectively.According to the composition of forces,the relation between the normal force and totaldeformation can be derived.Because of the plastic deformation and friction between asperities,the curves of the loading and the unloadingnotcoincide,and there isahysteresis loop.One cycleofenergy dissipation can be calculated by integrating theareaof the hysteresis loop,which includes the strain energy dissipation and the friction energy dissipation.The simulation analysis shows that：theenergy dissipation nonlinear increasesw ith the increaseof thedeformation.Thebigger contactangles the more energy dissipation,and it’s themostobvious in the elastic stage.There are only the friction energy dissipation in the elastic stage,so under the low loadsmustuse the assumption of double rough surfaces.In the plastic stage,there are only the strain energy dissipation,and the e ff ects of the contactangle on the energy dissipation are very little,so under theheavy loadscan use theassumption of thesingle rough surface to study themechanical interface.Comparingw ith the KE and Etsionmodels,ourproposedmodel iswellagreed w ith the Bartier’sexperiments.

interfaces，asperity，lateral contact，interaction，energy dissipation

TH113

A

10.6052/0459-1879-17-103

2017-03-27收稿，2017-04-20录用,2017-04-25网络版发表.

1)国家自然科学基金(51275407,51475363)，陕西省自然科学基础研究计划(2015JM 5246)资助项目.

2)傅卫平，教授，主要研究方向：机电系统动力学及控制、智能机器人、智能车辆控制理论与技术、现代物流系统工程与技术.E-mail：weipingf@xaut.edu.cn

高志强,傅卫平,王雯,康维超,吴洁蓓,刘雁鹏.弹塑性微凸体侧向接触相互作用能耗.力学学报,2017,49(4)：858-869

Gao Zhiqiang,FuWeiping,WangWen,KangWeichao,Wu Jiebei,Liu Yanpeng.Study on the contactenergy dissipation of the lateral and interactionalbetween theelastic-plastic asperities.Chinese JournalofTheoreticaland Applied Mechanics,2017,49(4)：858-869