SMT求解技术的发展及最新应用研究综述
2017-08-12吕荫润王秀利王永吉
王 翀 吕荫润 陈 力 王秀利 王永吉
1(基础软件国家工程研究中心(中国科学院软件研究所) 北京 100190)2(中国科学院大学 北京 100049)3(计算机科学国家重点实验室(中国科学院软件研究所) 北京 100190)4 (中央财经大学信息学院 北京 100081)
SMT求解技术的发展及最新应用研究综述
王 翀1,2,3吕荫润1,2,3陈 力1,2,3王秀利4王永吉1,3
1(基础软件国家工程研究中心(中国科学院软件研究所) 北京 100190)2(中国科学院大学 北京 100049)3(计算机科学国家重点实验室(中国科学院软件研究所) 北京 100190)4(中央财经大学信息学院 北京 100081)
(wangchong@nfs.iscas.ac.cn)
可满足性模理论(satisfiability modulo theories, SMT)是判定一阶逻辑公式在组合背景理论下的可满足性问题.SMT的背景理论使其能很好地描述实际领域中的各种问题,结合高效的可满足性判定算法,SMT在测试用例自动生成、程序缺陷检测、RTL(register transfer level)验证、程序分析与验证、线性逻辑约束公式优化问题求解等一些最新研究领域中有着突出的优势.首先阐述SMT问题的基础SAT(satisfiability)问题及判定算法;其次对SMT问题、判定算法进行了总结,分析了主流的SMT求解器,包括Z3,Yices2,CVC4等;然后着重介绍了SMT求解技术在典型领域中的实际应用,对目前的研究热点进行了阐述;最后对SMT未来的发展前景进行了展望,目的是试图推动SMT的发展,为此领域的相关人员提供有益的参考.
可满足性模理论;SMT求解器;SMT求解算法;测试用例自动生成;程序缺陷检测;云计算
近年来,随着可满足性模理论(satisfiability modulo theories, SMT)的不断进步以及互联网、云计算等新兴技术的不断发展,SMT被广泛地应用于各个领域,例如云计算与云存储[1-2]、访问控制[3-4]、多核问题[5-6]、程序缺陷检测验证[7]、有界模型检测[8-9]、RTL验证[10]、优化问题求解[11-12]、静态分析[13-14]、程序验证[15-16]等等.这些领域中待解决的实际问题都可以建模为约束可满足问题,SMT在这类问题的表述和求解上有突出优势.
计算机科学和数理逻辑中的SAT(satisfiability)问题是命题逻辑公式的可满足性问题.1971年,Cook[17]证明了SAT问题是非确定性多项式完全(non-deterministic polynomial-time complete, NPC)问题,SAT问题也是第1个被证明了的NPC问题.
起初,人们注重研究SAT在硬件测试、电路验证等领域中的应用,SAT求解技术的发展对自动电子设计(electronic design automation, EDA)领域中相关问题的研究起到了重要作用.随后SAT被广泛地应用于各个新兴领域,例如静态程序分析[18-20]、测试用例生成[21-23]等.SAT只面向命题逻辑公式,表达能力有较高的局限性,因此将实际问题转化为SAT问题时会丢失很多高层级(high-level)信息.例如在RTL验证中,SAT使用位向量描述原问题会导致大量逻辑信息的丢失,降低了结果的准确性.
由于上述缺点,人们将SAT扩展为SMT.SMT面向一阶逻辑公式,在命题逻辑的基础上补充了量词和项,具有更强的表达能力.SMT融合了多种背景理论,公式中的命题变量可以是理论公式,能够直接描述问题中的高层级信息.例如SMT的数组理论能直接描述数组定义和相关操作.实际应用中的理论不仅限于单一理论,通常是多个理论的组合.比如线性逻辑约束公式优化问题求解[11]需要线性实数理论和未解释函数理论等理论的支持;有界模型检[7]测需要数组理论、未解释函数理论和位向量等理论的支持;验证条件分析和定理证明[24]需要数组理论、未解释函数和线性整数算术理论等理论的支持.
SMT求解技术的具体实现被称为SMT求解器(SMT solvers).最初的SMT求解器[25-27]是研究人员为形式化方法设计的判定算法,直到1990年,可以处理大规模实际问题的SMT求解器[28-32]成为了新的研究热点.近年来,SMT求解技术的发展情况如下:
1) 核心算法、数据结构以及现代微处理器的发展使得SAT求解器[33]可以处理含有数万变量的公式,以SAT求解器为基础的SMT求解技术随之提升;
2) SMT求解技术的广泛应用前景使得各个科研机构积极开发SMT求解器;
3) 年度SAT竞赛*http:www.satcompetition.org和SMT竞赛*http:www.smtcomp.org推动了SMT求解技术的发展;
4) SMT-LIB(satisfiability modulo theories library)标准的出现使得SMT求解器开发变得更加容易.人们研发了很多SMT求解器,比较成熟的有Z3[34],CVC4[35],Yices2[36],MathSAT4[37],Boolector[38].SMT求解器也被集成到一些大型工具中,例如微软开发的PEX[39]工具,其主要功能是研究和分析托管代码.Henzinger等人[40]开发的BLAST工具是一个C语言软件模型检测工具,其实现主要依赖于谓词抽象和插值技术.
国内外研究人员对SMT进行了相关的研究和总结.王建新等人[41]给出了SAT问题定义和分类的综述,对各类衍生SAT问题进行了阐述和举例说明;Sheini等人[42]阐述了SAT和SMT的基本概念,介绍了基于SAT技术的SMT问题及求解方法等内容;Moura等人[43]对SMT求解技术和背景理论进行了详细地介绍;金继伟等人[44]对SMT求解技术进行了简述,包括SMT的部分背景理论、SMT判定算法及优化,重点介绍了SMT的基础知识及SMT求解器的基本情况.
SMT的实际应用是目前的研究热点,但是缺乏对SMT最新应用及最新进展进行综述的文章,也缺乏对SMT竞赛进行归纳和分析的文章.本文试图全面地介绍SMT在工业界和学术界中的最新主流应用,并根据目前SMT领域中公认度最高的SMT-COMP(international satisfiability modulo theories competition),比较主流SMT求解器的综合性能及支持背景理论的数量.为了文章的完整性以及易于后续研究人员理解,本文从SMT的起源,即SAT问题开始,简洁而又力求全面地介绍SMT的发展过程,详细阐述SAT,SMT判定算法及理论组合判定算法,分析算法的原理及实现过程,希望对程序分析与验证、软件缺陷检测等领域的研究提供支持.
1 SAT问题及判定算法
1.1 SAT问题
SAT问题是命题逻辑公式(propositional logical formula)的可满足性判定问题,下面先介绍有关命题逻辑的一些必要概念.命题逻辑中的逻辑运算符号(又称二元连接符)是指定义在布尔集合上的逻辑运算,包括∧(与),∨(或),(非),→(蕴含),↔(等价),⊕(异或).命题变元的取值为真或为假,在取值意义上等价为布尔变量.命题逻辑公式的形成规则为
1) 命题逻辑公式f(或SAT公式f)可以是单独的命题变元,也称为原子公式;
2) 如果f是命题逻辑公式,那么f也是命题逻辑公式;
3) 如果f1和f2是命题逻辑公式,那么f1⊥f2也是命题逻辑公式,其中⊥∈{∧,∨,,→,↔,⊕}.原子公式f与其否定命题f统称为文字,而1个子句由若干个文字析取而成.
基于命题逻辑,SAT问题可以进一步被描述为:给定1个命题逻辑公式f,公式f由子句集S组成,其中S由1组布尔变量V组成,判定是否存在1组对于f的赋值使得f中所有子句取值为真,如果存在,则称公式f可满足;否则,f不可满足.判定f是否可满足是SAT问题的核心.
随着SAT求解技术不断的发展,SAT问题的衍生问题也成为了研究热点,例如带权可满足性问题(weighted satisfiability)[45]、参数化带权可满足性问题(3-CNFSAT,q-CNFSAT)[45]、最大可满足性问题(maximum satisfiability)[46]、带权最大可满足性问题(weighted MAX-SAT)[47]、参数化MAXSAT问题[48]、参数化Almost2-SAT问题(parameterized2-ASAT)[48]等.
1.2 SAT问题判定算法
SAT问题判定算法可以分为2类:局部搜索算法和完备算法(回溯搜索算法).局部搜索算法基于随机搜索策略,对于任意给定的问题,它不一定能判断该问题是否可解;而完备算法基于穷举和回溯的思想,可以判断给定的问题是否可满足,对于无解问题拥可给出无解的证明.判定SAT问题时,需要确定给出的问题是否可满足,因此完备算法是研究的重点.
基于搜索回溯的SAT问题判定算法由Davis和Putnam在1960年提出,称为DP(Davis-Putnam)算法[49].该算法不适用于大规模命题公式的可满足性问题判定,因此Davis,Putnam,Logemann,Loveland对DP算法进行了改进,改进后的算法称为DPLL(Davis-Putnam-Logemann-Loveland)算法[50].
DPLL算法包括的主要操作为推理(unit-propagation)、纯文字(pure-literal)、决策(decide)、不可满足(fail)和回溯(backtrack).
unit-propagation对于子句取值未定义并且只含1个取值未定义的变量,可以直接令该变量取值为真并加入到赋值中,并根据当前赋值情况对搜索空间进行裁剪.若文字l在赋值中被判定为真,则公式f中所有含有l的子句都可以从搜索空间中删除,含有l的子句可以将l去掉.
pure-literal规则用于化简公式f中的变量,若f中仅存在l或l中的1种形式,则l的值可以立即被判定并从搜索空间中删除包含l的子句.
decide通过一些策略来选取1个尚未赋值的变量,并将它的值指定为真或假.
fail用于检测公式f在当前搜索空间下的可满足性以及是否存在冲突.
backtrack在fail检测到公式f在当前搜索空间不可满足时进行回溯,返回到上1层搜索空间并通过decide重新寻找赋值变量.
DPLL算法的输入是SAT公式f,输出为真(true)或者假(false),主要步骤如下:
1) 使用fail操作判断f的可满足性,如果不可满足则返回false;
2) 使用decide操作对f中1个未赋值的变量进行赋值;
3) 使用unit-propagation操作裁剪搜索空间;
4 )使用pure-literal规则化简f;
5) 使用fail判断f的可满足性,若f可满足,则返回true;
6) 使用fail判断f是否存在冲突,如果f不存在冲突,则返回步骤2,否则使用backtrack进行回溯;
7) 如果回溯失败,则返回false,否则执行回溯并返回步骤2.
现代DPLL搜索算法均是在此基础上进行改进的,典型的基于冲突检测的子句学习求解算法CDCL(conflict-driven clause learning SAT solver, CDCL)描述如下所示:
算法1. CDCL求解算法.
CDCL(f,v)
UnitPropagation(f,v)
if (ConflictDetection()=Conflict)
returnunsatisfiable;
end if
DecisionLevel=0;
while (notAllVariableAssigned())
(x,v)=FindBranchingVariable(f,v);
DecisionLevel=DecisionLevel+1;
UnitPropagation(f,v);
if(ConflictDetection()=Conflict)
ConflictLevel=ConflictAnalysis(f,v);
if(ConflictLevel<0)
returnunsatisfiable;
else
Backtrack(f,v,ConflictLevel)
dl=ConflictLevel;
end if
end if
end while
returnsatisfied.
CDCL算法与DPLL算法的最大区别在于每当UnitPropagation执行完成后,ConflictDetetction便会检测是否存在冲突,若存在冲突,则调用ConflicAnalysis分析冲突产生的原因并进行子句学习,以此确定回溯的层次.
现代SAT求解器采用了加速搜索的相关策略,例如启发式变量决策提升了decide操作的效率,学习子句删除减少了内存的消耗和性能的损失,搜索重启有利于对变量的决策顺序进行调整.研究人员也提出了一些改进的求解算法,比如Prestwich[51]在2006年提出的RANGER算法结合了贪心随机算法,求解速度比回溯算法快.Audemard等人[52]在2007年提出了GUNSAT算法,该算法的核心是局部搜索算法,可以求解不可满足问题.许道云等人[53]在2007年提出了带文字改名策略的DPLL算法,使用文字改名规则、消解规则、子公式规则和重复规则完成不可满足公式的反驳证明工作.
2 SMT问题及判定算法
2.1 SMT问题及背景理论
SMT问题的基础是一阶逻辑公式,在命题逻辑的基础上补充了项和量词,公式中的函数和谓词符号需要用对应的背景理论解释.通常情况下,SMT公式是无量词(存在、任意)的一阶逻辑公式(quantifier free formula),判定公式可满足性的问题称为SMT问题.
使用SMT描述实际问题并将问题等价的转化为SMT公式时,需要将一些数学理论、数据结构理论与公式相结合,这些理论称为SMT背景理论,可以增强SMT公式的表达能力.基于背景理论的SMT问题可以进一步被描述为:给定1个背景理论T和1个SMT公式F,F是T-可满足的(T-satisfiable)[54]当且仅当存在1个赋值使得公式F和背景理论T同时满足,即F∪{T}是可满足的.
SMT-LIB[55]是公认程度较高的SMT研究标准,主要包括:
1) 规定了SMT求解器标准输入输出的语言规范;
2) 建立了格式严格统一的背景理论知识测试集,用来评价和比较SMT求解器的求解能力;
3) 提出了SMT背景理论的规范,主要分为未解释函数理论(quantifier free_uninterpreted function, QF_UF)、数组理论(quantifier free_arrays, QF_AQF_AX)、整数集实数集上的线性算数理论(quantifier free_linear integer arithmeticquantifier free_linear real arithmetic, QF_LIAQF_LRA)、整数集实数集上的非线性算数理论(quantifier free_non_linear integer arithmeticquantifier free_non_linear real arithmetic, QF_NIAQF_NRA)、整数差分逻辑理论(quantifier free-difference logic over the integers, QF_IDL)、实数差分逻辑理论(quantifier free_difference logic over the reals, QF_RDL)、位向量理论(QF_BV)等.
在目前的实际应用中,主流SMT求解器支持并实现的主要理论有6个:
规则1. 如果i=j,则有select(store(array,i,v),j)=v.
规则2. 如果i≠j,则有select(store(array,i,v),j)=select(a,j).
数组背景理论中的相等关系需要通过未解释函数理论进行定义,例如(array=array′∧i=j)被等价地定义为(select(array,i)=select(array′,j)).基于QF-UF可以对数组背景理论可以进行如下扩展:
规则3. 对于2个相等的数组array和array′,任意1个整数(并且是数组的下标)i使得等式select(array,i)=select(array′,i)成立.
规则4. 对于2个不相等的数组array和array′,存在1个整数(并且是数组的下标)i使得等式select(array,i)≠select(array′,i)成立.
2) QF_IDL和QF_RDL.这2种理论的公式通常表示为
x1-x2⊙J,
(1)
其中,x1和x2表示实数或者整数变量,⊙∈{=,≥,≤,≠},J是1个常量.
3) QF_UF.此背景理论中主要包含没有经过解释的函数符号,比如f(x,y),g(h(z))等,每个函数符号都可以被赋予不同的含义.
4) QF_BV.此理论主要用于处理位向量相关操作,例如左移、右移等.
c1x1+c2x2+…+cixi+…+cnxn⊙J,
(2)
其中,c1,c2,…,cn为常系数,x1,x2,…,xn为整数变量(在理论QF_LIA中)或实数变量(在理论QF_LRA中),⊙∈{=,≥,≤,≠}.
求解线性不等式集是QF_LIA或QF_LRA理论的1个主要应用,比如F=x>3∧y<4,令x=6∧y=3可使F为真.
以上介绍了目前应用较为广泛的主流理论,SMT-LIB目前支持的理论及相互之间的关系如图1所示.
一些主流SMT求解器(比如Z3,CVC3,Boolector)对线性、非线性、位向量等背景理论的描述为[7,55]

(3)

(4)

(5)

(6)

Extract(B,i,j)|SignExt(B,k)|ZeroExt(B,k),
(7)

(8)

Fig. 1 SMT-LIB background theories and their relations with each other[55]图1 SMT-LIB理论之间的关系[55]
其中,L代表布尔值表达式,由A和L组成,代表逻辑运算符非.con是逻辑连接符,包括合取(∧)、析取(∨)、蕴含(→)、等价(↔)、异或(⊕).B代表由整数、实数、位向量构成的项,~代表补运算,Const表示常量,Id表示变量.ite(cb,t1,t2)表示if-then-else,如果布尔表达式cb的值为真,则执行t1,否则执行t2.Extract(B,i,j)表示抽取位向量B的第i到第j位,产生1个新的长度为i-j+1的位向量.SignExt(B,k)表示用k个0扩展位向量B,形成新的长度增加了k位的带符号位向量.ZeroExt(B,k)跟SignExt(B,k)操作类似,区别在于ZeroExt(B,k)生成不带符号的位向量.op代表操作符,包括与(&)、或(|)、四则运算符(+,-,*,)、右移(≫)、左移(≪)、位向量的级联(@).
2.2 组合背景理论求解方法
由实际应用问题等价转化而成的SMT问题通常包含多种理论,需要结合数组、整数线性算数、实数差分逻辑等多种背景理论才能解释SMT公式F中每一项的含义,这种情况下单理论判定方法无法满足判定需求,需要组合理论判定方法的支持,主要方法有:Nelson-Oppen(NO)方法[58]、Delayed Theory Combination(DTC)方法[59]和Ackerman方法[60].

Fig. 2 The difference between NO and DTC图2 NO方法和DTC方法的区别
Nelson等人[58]于1979年提出的Nelson-Oppen方法是最为经典的组合理论求解方法,其他方法都是以此为基础改进而成的.Nelson-Oppen方法的前提是各个背景理论符号集不相交且各理论之间相互独立,每个背景理论Ti中的无量词SMT公式都需要有1个可满足赋值Mi(基于理论的模型).Nelson-Oppen方法首先在各个理论间传递含有共享变量的等式,称为接口等式(interface equation),然后各个理论将此接口等式加入到自己的约束条件中并进行可满足性判定.如果出现不可满足的理论,则此SMT公式是不可满足的,否则重复上述步骤直至没有新的接口等式可以传递.如果此时没有不可满足的理论,则此SMT公式是可满足的.Nelson-Oppen方法的缺点是过于依赖于共享变量的传递,并且提取共享变量又需要求解器进行纯化操作,需要各个背景理论间相互传递接口等式.负责的算法框架使得Nelson-Oppen方法求解效率低下.
Delayed Theory Combination方法由Bozzano等人[59]提出,避免了各个背景理论间的接口等式传递步骤,将组合理论的可满足性判定请求统一交给顶层求解器处理,简化了求解框架,求解效率好于Nelson-Oppen方法.Nelson-Oppen方法和Delayed Theory Combination方法的区别如图2所示.
Ackerman方法是Nelson等人[60]基于Nelson-Oppen方法提出的改进算法,主要用于求解含有未解释函数理论的组合背景理论问题,通常和DTC方法结合使用.但是此方法具有局限性,仅提升在未解释函数理论下SMT的求解效率.
2.3 SMT问题判定算法
2.3.1 求解SMT问题的积极类算法
积极类算法直接将SMT公式转化为可满足性意义上等价的SAT公式[61],然后利用SAT求解器进行求解工作.这个方法的好处在于它可以充分利用高效的SAT求解器,不用针对SMT的复杂背景理论去开发特定理论求解器,积极类算法是早期求解SMT问题的主要方法,主要包括Per-Constraint Encoding[62-63]方法和Small-Domain Instantiation[64-65]方法.
Per-Constraint Encoding方法是指:对于SMT公式F,如果F含有未解释函数,则通过Goel等人[66]提出的方法将SMT公式F转化为基于可满足意义上等价的SAT公式,主要思想是将F中的所有形如ai=aj的项用1个新的变元bij来表示,再用SAT求解器对公式F进行求解.bij需要满足传递性,即(bij∧bjk)→bik.
Small-Domain Instantiation方法是指:对于SMT公式F,如果F中的项只包含变元,则用布尔变量组成的位向量代替公式中的变元,将SMT公式转化为基于可满足性意义上等价的SAT公式,利用SAT求解器求解公式F的可满足性,达到求解原SMT公式可满足性的目的.如果公式F除了变元外还包含未解释函数,则需要利用Ackerman方法将公式F转化为只包含等式逻辑的公式,然后判定F的可满足性.
积极类算法的求解效率依赖于实际问题建模为SAT问题的效率和SAT求解器自身的效率.随着实际应用问题规模的不断增大,建模为SAT问题后得到的SAT公式长度呈现指数级增长的趋势,算法的时间开销难以接受.因此,这类算法并不适用于求解工业界的大规模实际应用问题.
2.3.2 求解SMT问题的惰性算法
惰性算法[29]是目前大多数SMT求解器采用的算法[67-69],算法主要步骤如下:
1) 对SMT公式进行预处理,把公式中的命题变量替换为布尔变量,再将SMT公式转化为可满足性意义上等价的SAT公式;
2) 检查此SAT公式是否可满足,如果不可满足,那么SMT公式也不可满足,算法结束;
3) 如果SAT公式可满足,则结合SMT背景理论去判断SMT公式的可满足性,返回判断结果,算法结束.
此算法的优势在于,若算法在步骤2中已判定SAT公式不可满足,则无需进行后续判定工作,提高了求解效率.惰性算法是SAT求解器与对应的背景理论相结合的产物,典型的惰性算法是DPLL(T)[70-71]算法.
DPLL(T)算法伪代码如下:
算法2. DPLL(T).
输入:SMT公式F;
输出:true(真)或者false(假).
预处理公式F得到F的SAT形式的公式f
if (f是不可满足的)
return false;
else
for (每个f的模型M)
检查M是否与背景理论一致;
if (存在一个与背景理论一致的模型M)
return true;
end if
end for
if (每一个模型M都与背景理论不一致)
return false;
end if
end if
DPLL(T)算法的基础是通用求解架构DPLL(X),此架构独立于具体的背景理论,将X替换为某个具体的背景理论T即可成为针对此背景理论的具体求解算法.但是在求解过程中,背景理论求解器的参与程度较小,通过理论预处理、选择分支、理论冲突分析、理论推导等技术可以提升背景理论求解器的参与程度,从而获得更高的求解效率[67-68,71-72],Sebastiani[73]使用优化技术同样达到了提高求解效率的目的.
一些研究人员注重于如何将SAT求解器与背景理论更好地结合以获得更高的求解效率,并做了相关的研究[67,74-75].
3 SMT求解器及性能比较
随着SMT背景理论的逐渐成熟以及SMT问题判定算法的不断发展,许多SMT求解器能够满足学术界的研究需求,一些成熟的SMT求解器也能处理大规模工业化的应用问题.目前主要的求解器有:Z3[34],CVC3[57],CVC4[35],Boolector[38],Yices2[36],MathSAT[76],Mathsat4[37],Verifun[75],Beaver[77],TSAT[78],Barcelogic[79],VeriT[80]等.下面重点介绍4个有代表性的SMT求解器.
Z3以其优秀的综合求解能力被业界所认可,是目前为止在扩展性、表达能力以及求解效率等方面都较为出色的SMT求解器.Z3的求解框架集成了基于DPLL的SAT求解器,并支持未解释函数、算术运算、数组等背景理论,核心求解算法是DPLL(T)算法和DTC方法.许多工业界的项目都用到了Z3,例如Pex[39],HAVOC[81],Yogi[82],SLAMSDV[83],Vigilante[84]等.
CVC3和CVC4是纽约大学和爱荷华大学联合开发的SMT求解器,使用SAT求解器和理论求解器的Search Engine作为核心求解框架,支持支持多种理论的求解.与CVC3相比,CVC4能更好地支持SMT-LIB并且优化了求解框架.
Yices2是SRI International计算机科学实验室开发的SMT求解器,前身是Yices,支持数组理论、线性算数运算理论、位向量理论,核心求解算法是优化后的同余闭包算法.在组合理论的求解方面,Yices使用位移等式改进了传统的Nelson-Oppen方法,并结合动态Ackerman方法进行求解.在实际应用领域,Yices作为定理证明的核心部件被整合到了SRI International开发的定理证明器PVS中.Yices2对Yices进行了优化和改进,减少了复杂类型的数量,只含有整数、实数、位向量和布尔变量4种原子类型并简化了类型的表示,例如将int(整数)类型视为real(实数)类型的子类型.Yices2提供了符合SMT-LIB标准的接口,增加了对元组和标量等数据类型的支持.
其他SMT求解器也都有各自的特点.例如,Barcelogic的核心求解算法为Ackerman方法、DTC方法以及位移等式策略.MathSAT4在结合了Ackerman方法和DTC方法的基础上,使用了动态Ackerman方法求解可满足性问题.Boolector可以求解含有位向量理论和可扩展的数组理论的可满足性问题.VeriT是基于改进的Nelson-Oppen方法开发的SMT求解器,仅支持无量词理论和整数差分理论的可满足性问题求解.
为了推动SMT求解技术及SMT求解器的进步,可满足性理论及应用国际学术年会自2005年开始,每年举办SMT-COMP竞赛,到2015年为止共成功举办了11届比赛.用于评判各个求解器求解能力的标准测试集来源于SMT-LIB,其数量从最初的1 400个增加到如今的10 000多个.标准测试集是由各个背景理论测试集组成的,例如线性算数测试集(LIA)、位向量(QF_BV)测试集等.表1包含了自2005年开始到目前为止每一届SMT-COMP的比赛结果.表1以每个SMT求解器所支持背景理论的数量、在不同背景理论测试集上的排名以及综合评分作为依据,在Winner一栏中列出了每一届比赛的冠军,并在Background Theories一栏中给出了对应SMT求解器在参赛时所用到的背景理论测试集,在这些测试集上该SMT求解器综合的求解效率要好于其他SMT求解器.由表1可以看出,Barcelogic获得了第1届竞赛的冠军,并在QF_UF等4个背景理论测试集上有着突出的表现.在随后的比赛中,Yices和Yices2也获得了冠军,支持背景理论的数量远远大于Barcelogic.在SMT-COMP2010中,CVC3也取得了不错的成绩.最近5年中,Z3始终排在第1位,支持背景理论的数量也在逐年增加,在大多数理论测试集上的求解速度快于其他求解器,综合性能较好.
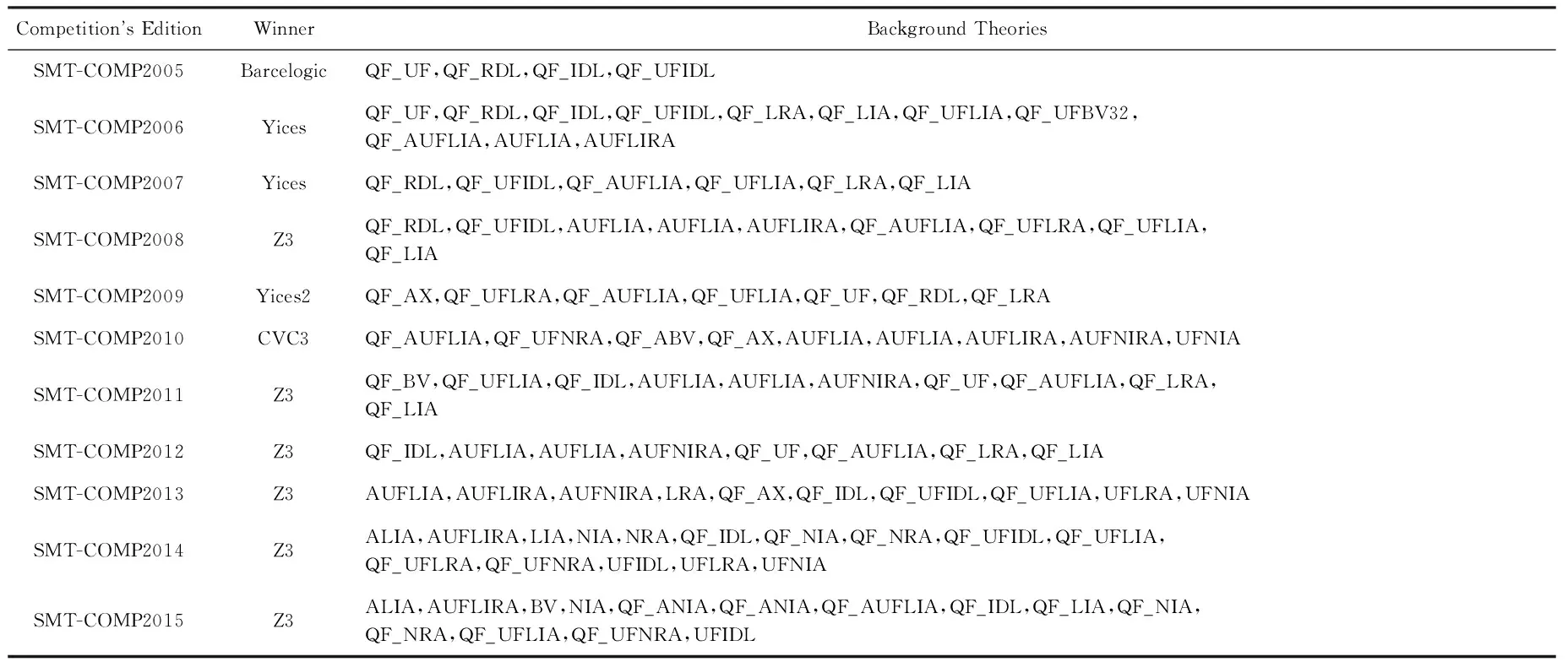
Table 1 Winners of the Each SMT-COMP Editions表1 历届SMT-COMP的冠军
表2是2015年SMT-COMP的比赛结果,Sequential Performances代表顺序性能的评分,Parallel Performances代表并行性能的评分,Normal和Industrail分别代表各个SMT求解器在标准测试集和工业测试集上的评分,以求解速度、支持的背景理论数量等因素为依据,在Rank一栏中给出了每个求解器的综合排名.
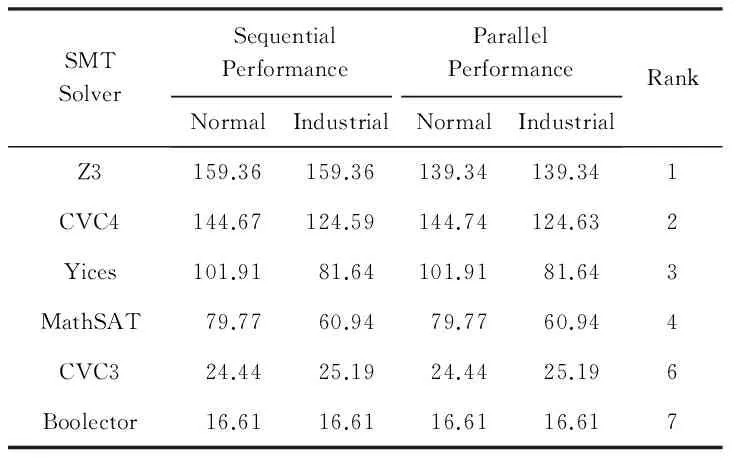
Table 2 Ranking of SMT-COMP 2015表2 SMT-COMP2015综合排名
由表2可以看出,无论是在标准集测试上还是在工业测试集上测试,Z3求解器的综合性能都要比其他SMT求解器好.Z3在标准测试集和工业测试集上的评分相同,说明Z3具有较好的稳定性,Z3的Sequential Performance的评分高于Parallel Performance的评分.排名第2的CVC4的评分与Z3相差不大,唯一的区别是在标准测试集和工业测试集上Parallel Performance的评分都略高于Sequential Performance的评分,是为数不多的在Parallel Performance的评分上取得较好成绩的求解器之一.Yices和MathSAT求解器评分低于Z3和CVC4,在2个测试集上的Sequential Performance的评分和Parallel Performance的评分均保持不变,较为稳定.CVC3和Boolecter的评分与其他求解器相差过大,无论是在标准测试集上还是在工业测试集上,求解大规模可满足性问题的能力都要低于其他求解器.
在2015年SMT-COMP中,举办方提供了40种不同的背景理论测试集,基于每个SMT求解器在各个测试集上的综合评分,表3给出了主流SMT求解器在不同背景理论测试集中的排名.其中LIA表示整数线性算数理论,QF_ABV表示无量词固定位向量数组理论,QF_IDL表示无量词整数差分逻辑理论,QF_NIA表示无量词整数非线性算数理论,QF_UFLIA表示无量词未解释函数的整数线性算数理论,“ ”代表此SMT求解器不支持对应理论的求解.从表3中可以看出,Z3求解器支持主流的背景理论数量最多.

Table 3 Ranking of SMT Solvers Based on Different Background Theory’s (SMT-COMP 2015)表3 不同背景理论下的SMT求解器排名 (SMT-COMP 2015)
4 SMT应用
随着SMT判定算法的不断发展以及SMT求解器的逐渐成熟,人们开始使用SMT解决一些实际问题,例如测试用例自动生成、程序缺陷检测、RTL验证、程序分析与验证、线性逻辑约束公式优化问题求解等.
4.1 测试用例自动生成
4.1.1 基于SMT的测试用例自动生成
测试用例自动生成是设计和编写软件测试用例一种方法,也是软件测试的一种重要手段,常用于检测程序缺陷.基于SMT的测试用例自动生成技术主要分为获取程序执行路径和检查路径可满足性这2个部分.获取程序的执行路径主要依赖于动态符号执行,即在不执行程序的前提下,使用具体数值代替程序变量作为程序的输入,模拟程序的执行,分析1条指定路径会触发程序中哪些代码的执行,并记录下此路径.检查路径可满足性需要将程序执行路径转化为SMT公式,然后使用SMT求解器判断公式的可满足性.具体思想如下:首先利用基于动态符号执行的代码模拟执行器模拟一条具体的程序执行路径,同时记录路径中的条件语句和赋值语句,再通过SMT背景理论将这些语句转化为SMT公式F,例如可以用未解释函数背景理论将赋值语句表示为等式的合取形式,而数组赋值语句则需要数组理论的支持,利用SMT求解器对判断F的可满足性,此时会出现2种情况:
1) 如果F可满足,F的具体可满足性赋值可作为该条路径的输入(测试用例).通过修改F中的某个条件,例如将分支语句if(a=0)中的表达式(a=0)改为(a!=0),可以构建出1条新的执行路径,将新的路径转化为公式F′,通过SMT求解器求解F′,得到新的输入(测试用例),利用新的输入再进行新一轮的路径构造、约束求解.通过这种迭代的路径生成方法,动态符号执行可以持续遍历程序的可执行路径,直到所得到的测试用例数量达到预期值,从而实现了测试用例的自动生成.
2) 当F不可满足时,说明当前执行路径不正确,修改某一分支语句的分支条件后进行新一轮的路径构造、约束求解.
4.1.2 具体示例
图3(a)中函数addition()是1个加法函数,函数输入choice的不同取值会产生不同的执行路径,从而影响sum的取值.图3(b)是addition()的2条执行路径.
基于SMT的测试用例自动生成的过程如下:首先使用代码模拟执行器得到addition()的1条执行路径,即图3(b)中的路径1,将路径1转化为SMT公式,记为
F1=(a=0)∧(choice>1)∧(sum=2),
(9)
利用SMT求解器判断出F1是可满足的,且可满足解为(choice=2),从而得到了第1个测试用例.然后将if语句中的表达式取反,得到图3(b)中的路径2,将路径2转化为SMT公式,记为
F2=(a=0)∧(choice≤1)∧(sum=2),
(10)
利用SMT求解器判断出F2是可满足的,且可满足解为(choice=1),达到了测试用例自动生成的目的.

Fig. 3 Record the number of requests
图3 记录请求次数
4.1.3 SMT在测试用例自动生成中的应用
许多成熟的工具中都用到了基于SMT的测试用例自动生成方法,例如Pex[39]工具将.Net组件和基于SMT的测试用例自动生成技术相结合,使用Z3求解路径的可满足性,可以自动生成.Net程序的测试用例,例如C#程序.Pex也为含有复杂数据结构的程序提供测试用例自动生成的功能.
SAGE[85]是1个白盒测试工具,使用代码覆盖率检查工具Nirvana和约束产生工具TruScan将程序路径转化为SMT公式,利用Z3求解公式的可满足性并自动生成新的测试用例,结合微软模糊测试的基础框架,SAGE可以找出程序中的大多数错误.
JPF-SE[86]工具利用符号执行技术获取程序的执行路径并转化为SMT公式,使用Yices求解路径的可满足性并生成测试用例并作为输入提供给工具内的其他组件.
Yogi[82]是1个基于SMT的C语言静态分析和测试工具,该工具使用Z3求解程序路径的可满足性并产生测试用例,被集成到微软的静态驱动检测框架中,完成了69个Windows Vista的驱动检测工作.
Arcaini等人[87]提出了一种使用区分配置(dis-tinguishing configuration)检查特征模型错误的方法.该方法利用Yices求解测试谓词(test predicate)的可满足性,如果可满足,则具体的可满足赋值即为区分配置(distinguishing configuration),使用区分配置作为测试用例进行特征模型的错误检查工作,实现了测试用例的自动生成;如果不可满足,则产生特征模型的突变(mutated)模型.
4.2 程序缺陷检测
4.2.1 基于SMT的程序缺陷检测
程序缺陷检测的目的是检查程序是否违反了给定的安全属性,例如是否有死锁、是否存在安全漏洞等.软件测试是检测嵌入式程序缺陷的一种常用方法,所需的测试用例可以由人工编写或者使用动态符号执行等技术自动生成.当程序规模很大时,很难获取覆盖程序所有执行路径的全部测试用例,时间开销也是难以接受的.因此,软件测试只适用于寻找软件的缺陷,无法保证程序不含有某个指定的缺陷.基于模型检测[88]的程序缺陷检测方法是一种自动检测技术,通过对程序进行抽象得到1个有限的状态空间,减少了缺陷检测带来的时间开销,在一定程度上减小了缺陷检测的难度.但是程序规模的不断增大导致状态空间也随之增大,状态空间爆炸是模型检测不可避免的问题.
基于SMT的有界模型检测(bounded model checking,BMC)方法成为了新的研究热点.主要思想是检测程序在界限K内是否满足给定的安全属性(property),给定系统I,1个安全属性P,以及1个界限(bound)K,BMC会将系统I展开K次得到验证条件V,V是可满足的当且仅当P在界限K内有1个反例.这里的界限K是指将源程序中的循环结构(比如for循环)展开K次.V是源程序所转化成的等价SMT公式F.基于SMT的有界模型检测是指将上述F与P的反(F∧P)送入SMT求解器,如果(F∧P)可满足,证明程序的某一条执行路径会违反安全属性,通过SMT求解器返回的具体可满足赋值可以得到使得程序出错的具体输入,如果(F∧P)不可满足,则证明程序在界限K内不违反安全属性.
4.2.2 具体示例
下面用1个例子说明SMT求解器在程序缺陷检测中的应用.图4(a)是1个C语言程序,其功能是计算斐波那契数列第n项的数值,并将结果存在整型数组result[0]中.斐波那契数列是指这样1个数列:数列的第0项为0,第1项为1,第2项为1,并且从第2项起,每一项都是前2项的数字之和,例如,斐波那契数列的前6项为:0,1,1,2,3,5.图4(b)表示函数Fib(intn)的静态单赋值(static single assignment, SSA)形式,SSA形式与源程序的区别在于2点:1)SSA形式中的每个变量名仅被赋值1次.对于同一变量的多次赋值采用“原变量名+赋值次数”的形式来取代原变量名;2)SSA形式中消去了原程序中的循环结构(比如while),利用循环体展开的形式等价表示循环结构.图4(b)是将源程序中的while循环展开3次的结果.图4(c)是将SSA形式中的语句进行合取得到的等价表示形式,称为SMT公式F.程序中存在数组result,需要检查是否存在数组越界问题,由于数组只含有1个元素,因此安全属性P可以被表示为(j=0).SMT求解器将逻辑公式(F∧P)作为输入,通过结合相应的背景理论(例如本程序需要用到未解释函数理论)对公式F的可满足性进行求解,可知(F∧P)不可满足,程序不存在数组越界问题,没有违反给定的安全属性.

Fig. 4 Converting the source code into the SMT formula
图4 源程序转化为SMT公式
4.2.3 SMT在程序缺陷检测中的应用
基于SMT的有界模型检测方法中的界限K使得此方法在医疗、通信等嵌入式程序的验证中有着很大的优势.原因在于相对于一般软件,嵌入式程序的代码量小,且嵌入式程序不鼓励使用大量的递归和循环语句,很少见到循环次数超过K的循环体,只需要证明程序在K步内满足安全属性即可.
Cordeiro等人[7]在2012年提出了一种基于有界模型检测的嵌入式软件缺陷检测方法.此方法先将嵌入式程序的ANSI-C语言源文件转化为控制流图(control flow graph,CFG),再把CFG对应的GOTO-Program转化为SSA形式,对SSA进行处理并提取出用户断言和安全属性后得到与源程序等价的SMT公式,然后使用Z3或者Boolecter求解公式的可满足性,根据求解结果判定该嵌入式程序是否满给定的安全属性.此方法在软件ESBMC(efficient SMT-based context-bounded model checker)中得以实现,图5是ESBMC的结构图,描述了ESBMC进行有界模型检测的步骤.ESBMC支持ANSI-C语言中许多数据结构、变量的检查,其中包括标量数据类型(比如整型、长整型等)、固定点算数、算术溢出、数组、结构体、指针、动态内存分配等.ESBMC会将它们转化为与SMT背景理论相符合的公式,再将公式送入SMT求解器求解.

Fig. 5 Overview of the ESBMC architecture图5 ESBMC结构概览
Ramalho等人[89]在2013年提出了基于SMT的C++程序缺陷检测方法,可以检测C++语言中的标准库函数以及C++特有的模板、容器、继承、异常的缺陷.C++库函数在有界模型检测中会产生大量复杂而又冗余的验证条件,因此,Ramalho等人[89]为C++的库函数建立C++操作模型(C++ operational model, COM),作为C++库函数的简单表示,在保证有界模型检测的正确性的同时减少了产生的验证条件的数量,并使用Z3等SMT求解器判定验证条件的可满足性,提高了验证效率.COM中包含ANSI-C库函数,保证了对ANSI-C语言检测的支持.
Cordeiro等人[90-91]提出了基于SMT的多线程软件上下文界限模型检测方法,可以检测多线程软件的缺陷.文中把多线程并发视为以不同顺序激活不同线程的线性序列,将程序的所有可达状态记为状态空间W,将线性序列、可达状态已经安全属性转化为SMT公式,利用Z3等SMT求解器求解公式的可满足性,判断每一个状态是否会违反安全属性.通过可达树(reachability tree, RT)、惰性方法(lazy approach)、调度算法以及下近似和展开方法(under-approximation and widening approach)完成了多线程软件的模型检测工作.文中还对Pthread library[92]进行了建模,包括互斥锁操作、条件等待等操作.
Pereira等人[93]在2016年提出了基于SMT的统一计算设备架构(computer unified device architecture,CUDA)程序上下文界限模型检测方法,CUDA是由NVIDA[94]开发的1个并行编程平台和应用编程接口模型,目的是为了充分利用GPU(graphics processing unit)的能力.他们在ESBMC的基础上开发了ESBMC-GPU,能很好地对CUDA函数库进行建模,并利用SMT进行模型检测工作.为了缓解多线程环境下状态复杂的问题,他们将单调偏序规约(monotonic partial order reduction,MPOR)应用到CUDA程序中来消除冗余的程序执行路径和RT[95]中的冗余状态.
基于SMT的模型检测工具在工业界也得到了应用,Ball等人[96]使用SLAM工具对Windows NT驱动程序进行了模型检测工作,检测了其中是否存在死锁等问题.
4.3 RTL验证
4.3.1 基于SMT的RTL验证
RTL验证是检验集成电路功能性错误的方法.随着集成电路规模的不断增大,普通模拟验证已经无法满足大规模集成电路验证的需要,因此,形式化验证受到了高度的关注.目前工业界采用了一些SAT求解器处理求解门级电路的问题,比如Minisat和BerkMin等.研究人员也对SAT求解器在电子电路验证中的应用做了相关研究[97],并提出了自动测试图样产生(automatic test pattern generation, ATPG)、整数线性规划(integer linear programming, ILP)、超图划分等求解方法[98].但是这些方法求解门级电路所需要的时间开销让人难以接受,因此,基于SMT的RTL混合可满足性求解方法是目前的研究热点.
4.3.2 具体示例
下面用1个简单的例子来说明SMT在RTL验证中的应用.如图6所示,电路E只含有1个与门和1个或门,需要验证是否存在1组输入使得电路输出结果Z为1(真).具体步骤如下:首先根据电路图结构将E转化为等价的SMT公式F=(a∧b)∨c,再利用SMT求解器求解F的可满足性,可知当a=1,b=1,c=0时,F可满足:即Z=1,达到了验证的目的.
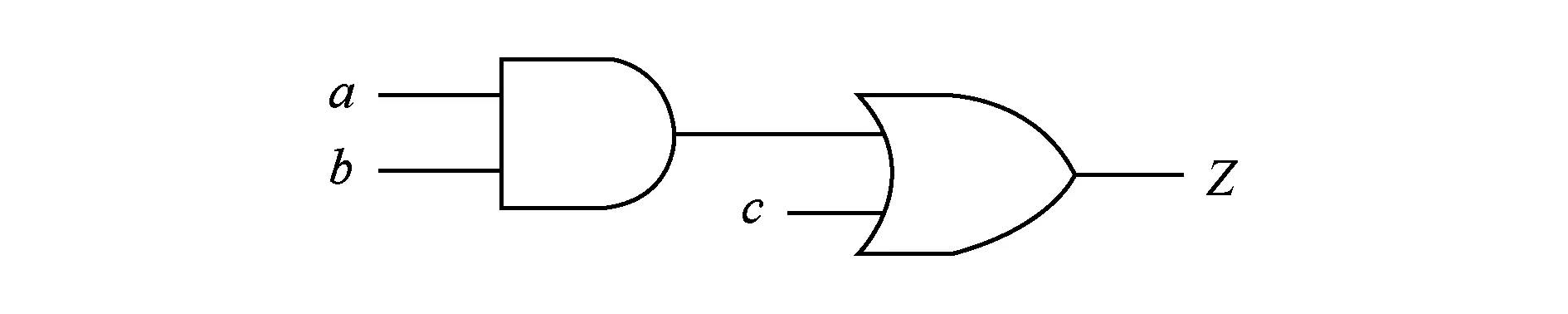
Fig. 6 Circuit diagram E图6 电路图E
4.3.3 SMT在RTL验证中的应用
许多形式化验证工具,包括一些工业界采用的工具都是通过位级模型实现RTL验证,主要思想是将高层级的RTL设计转化为位级信息,再对位级信息进行展开验证工作.这种方法不能充分利用高层级所含的结构,在转换中会丢失高层级的信息,可扩展性低.
Kroening等人[99]提出了一种利用高层级信息模型进行RTL验证的方法,该方法利用谓词抽象技术和SMT求解器进行位级以及字级的验证(word-level verification).结合了反例指导的抽象框架[100](counterexample guided abstraction refinement frame)的谓词抽象技术将系统的实际状态空间映射到1个抽象的、状态数较少的空间中,并在系统表现出的特性上与原有系统保持一致.图7是RTL Verilog谓词抽象技术的大体框架.

Fig. 7 The predicate abstraction techniques of RTL verilog图7 RTL verilog的谓词抽象技术
Puri等人[101]提出了基于SMT的自动RTL测试生成器SI-SMART(swarm intelligence-SMART),目的是解决传统有界模型检测方法和基于符号执行的检测方法对循环处理能力不足的问题.在DUT(design under test)中,循环是很常见的,但是有界模型检测或者基于符号执行的检测方法只能将循环展开至多K次,再进行RTL验证工作.此方法不适用于DUT.SI-SMART先对DUT中的循环进行抽象,再找出直接或间接影响目标分支条件的变量,分析它们之间的递推关系技术并以此消除控制流图中的循环展开,从而解决了需要按照一定界限展开循环的问题.
Brady等人[102]提出了硬件设计的自动项级(term-level)抽象技术,是一种基于形式化逻辑的、针对字级设计的抽象技术,所有数据用抽象的项、功能函数和未解释函数等形式表达,解决了目前大多数抽象技术所面临的抽象等价性问题,即是否可以把组件C等价的抽象为另一个表示C′.此抽象技术先利用随机模拟技术检验功能模块是否可以用未解释函数来抽象,再利用静态分析技术计算抽象条件,最后利用SMT求解器验证项级抽象结果的可满足性.目前这种技术已经成功的应用于处理器设计验证、接口逻辑验证等领域.
赵燕妮等人[103]利用SMT求解RTL的可满足性问题,其主要思想是将RTL电路视为1个超图,然后基于超图划分的方法得到1个割集最小的等量超图划分,形成有限个超图子问题,再利用Yices求解子问题的可满足性.
Gent等人[104]提出了基于有界模型检测和群体智能的RTL功能测试方法,该方法使用HYBRO[105](hybrid analysis and branch coverage optimizations)抽取特定的程序执行路径并将其转化SMT公式,利用Z3求解这些SMT公式的可满足性,再结合有界模型检测的方法进行RTL验证.
Kunapareddy等人[10]对LPSAT和SMT在RTL验证中的应用进行了比较,结论表明:基于Z3的RTL验证方法在代码复杂度、执行时间和迭代次数上的表现均优于LPSAT方法.
4.4 程序分析与验证
4.4.1 基于SMT的程序分析与验证
基于SMT的程序分析与验证是一种形式化方法,基础思想来源于Floyd和Hoare提出的弗洛伊德-霍尔逻辑(Floyd-Hoare logic).该方法将前置条件(pre-condition)、循环不变量(loop invariant)和后置条件(post-condition)以断言(assert)的形式引入程序验证中,三者分别判断程序在运行前、运行中以及运行结束时的正确性,通过判定断言得成立情况检验程序的正确性.
4.4.2 具体示例
用1个简单的程序来说明SMT在程序分析与验证中的应用.图8(a)是1个求最大公约数的程序GCD,x和y是程序的输入,m是程序中的辅助变量.为该程序加上pre-condition,loop invariant以及post-condition后得到的程序如图8(b)所示.具体过程如下:1)程序GCD的2个输入为正数是求解最大公约数的基本条件,即F1=(x≥0)∧(y>0).运算过程中的被除数要大于除数,即F2=(x≥y).将F1和F2加入到pre-condition中.2)在while循环中,x,y和m需要恒大于0且x要始终大于等于y,即F3=(x≥0)∧(y>0)∧(x≥y)∧(m≥0),将F3加入到loop invariant中.3)最大公约数是1个整数,即F4=(y≥0),将F4加入到post-condition中.然后通过动态符号执行技术遍历程序GCD的所有执行路径,再将这些路径转化为SMT公式F,然后将pre-condition,loop invariant以及post-condition转化为SMT公式并与F合并,记为F′,通过SMT求解器求解F′的可满足性,若F′不可满足,说明程序中含有错误,若F′可满足,说明在所有断言得到满足性的情况下,程序是正确的,验证了程序的部分正确性.本例中的程序GCD是正确的.

Fig. 8 Greatest common divisor program
图8 求最大公约数程序
4.4.3 SMT在程序分析与验证中的应用
2005年,Leroy[15]研发了1个C语言编译器CompCert,该编译器是经过形式化验证的优化编译器,主要功能是将C语言编译为PowerPC汇编代码,Leroy对编译的每一步操作给出了严格的数学证明,大大提高了CompCert的可信度.但是这种基于数学证明的程序分析与验证方法难度大、耗时长,因此,基于SMT的程序分析与验证成为了新的研究热点.
何炎祥等人[106]提出了使用SMT求解器进行路径敏感程序验证的方法,主要思想是通过最大强连通分量压缩循环路径并使用基于布尔表达式的方法对路径空间进行抽象,减少了待验证程序路径的规模,再结合动态符号执行技术和抽象解释技术将压缩后的程序路径转化为SMT公式,使用Z3求解公式的可满足性,如果可满足,证明路径是正确的,达到了程序验证的目的,否则说明路径会触发程序的某个错误.
在计算机编程中,需要在编译前确定变量的类型(例如float或double),变量精度会受到类型的影响,在程序输入不变的情况下,改变变量类型在某些情况下会使程序输出不同的结果.但是,在程序运行之前很难判断所选变量类型是否符合计算的精度.Paganelli等人[107]提出了一种通过增加精确度验证浮点数程序稳定性的方法,证明了增加变量精度会使得结果产生微小的变化.该方法首先分析程序中变量的类型以及用户的断言,计算出程序的最弱前置条件(weakest precondition),然后将最弱前置条件转化为SMT公式F并使用Z3求解F的可满足性,如果F可满足,则具体的可满足赋值可以作为程序的1个测试用例,作为后续证明过程的输入.如果不可满足,便需要用户对程序进行调整.
克雷格插值(craig interpolation)方法在程序验证领域取得了不错的成绩,例如Kroening等人[108]开发了基于克雷格插值的软件验证工具Wolverine.但当插值规模很大时,程序验证的效率可能会受到影响,因此Pigorsch等人[109]提出了一种基于SMT的减小interpolation规模的算法,可以提升克雷格插值方法的效率,MathSAT负责算法中公式的不可满足性的证明工作.
工业界的验证工具也用到了SMT求解器,例如,VCC[110](verifying C compiler)是1个低层级并发系统(low-level concurrent system)代码验证工具,集成了SMT求解器Z3,可以根据程序中的注释(比如函数功能、状态断言等)验证程序的正确性.微软使用VCC验证了虚拟化产品Hyper -V的正确性.
4.5 线性逻辑约束公式优化问题求解
4.5.1 SMT与线性逻辑约束公式优化问题求解
SMT在线性逻辑约束公式优化问题求解中的主要应用是:结合背景理论(例如线性实数理论),利用SMT求解器找到满足目标公式及约束条件的最优解.具体来说,首先根据实际问题的约束条件和优化目标抽象出约束表达式φ和目标函数H,再利用SMT求解器求出满足φ的可行解集G,然后找出G中使H达到最大值(或最小值)的可行解,即为最优解.
4.5.2 具体示例
结合Li等人[111]提出的基于SMT的线性逻辑约束公式优化问题求解方法,举1个简单的例子,给定基于线性实数算术理论的公式:
φ≡(1≤y≤3)∧(1≤x≤3∨x≥4),
(11)
其中,φ的可行域表示二维坐标系上的一片区域,x和y均为实数变量,分别位于坐标系的横轴和纵轴上,(x,y)代表坐标系中的1个点记为p=(x,y).目标函数为H={y,x+y}.需要在满足约束条件φ的情况下求出使目标函数H达到最大值的x和y,即(xopt,yopt),基于SMT的线性逻辑约束公式优化问题求解步骤如下:
1) 假设最优解为optT(φ),根据约束条件φ可将最优解的最小上界(under-approximation, UA)初始化为
UA≡y≤-∞∧x+y≤-∞,
(12)
最大上界(over-approximation, OA)初始化为
OA≡y≤∞∧x+y≤∞.
(13)
2) 将φ∧UA送入SMT求解器,求得可行解为(x=2)∧(y=2),记为p1=(2,2),更新最小上界为
UA≡y≤2∧x+y≤4,
更新最大上界为
OA≡y≤3.
3) 将φ中每个原子公式中的不等号替换为等号,得到的集合记为
ε(φ)={l=k|l≤k∈φ},
例如,此时ε(φ)={x=1,x=3,x=4,y=1,y=3}.点p的边界类定义为[p]=e∈ε(φ)|p|=e.[p1]=∅,因为此点不接触任一边界.提取目标函数H的第1个元素y,判断在满足y≤3的基础上,是否存在优于可行解p1的另1个可行解p2,即:
S≡[p1]⊂[p2]∧y(p2)≥y(p1),
其中,y(pi)代表点pi的y值.使用SMT求解器判断可行解p2是否存在,得到p2=(3,3),由ε(φ)可知x和y的取值都达到了各自的上界,因此,更新最优解的最小上界为
UA≡y≤3∧x+y≤6.
4) 将φ∧UA送入SMT求解器,求得可行解为(x=5)∧(y=3),记为p3=(5,3),更新最小上界为
UA≡y≤3∧x+y≤8.
5) 提取目标函数H的第2个元素x+y,在满足x+y≤∞的基础上,使用SMT求解器求得优于p3的可行解p4=(6,3),重复此求解步骤,发现x+y的值可以无限的增大,求解过程无法终止,判定此最优解为无穷大,即x+y是无上界的,因此,更新最优解的最小上界为
UA≡y≤3,
此时,UA≡OA,求解结束,得到最优解为
optT(φ)≡y≤3.
因此,xopt=∞∧yopt≤3.
4.5.3 SMT在线性约束优化问题求解中的应用
Sebastiani等人[11]提出了求解线性实数算术问题全局最优解的方法,主要思想是通过可行解测试(feasibility test)、查找关键点(critical finding)、全局检查(global checking)三个步骤来找到全局最优解.在可行解测试中,算法利用SMT求解器求出符合约束条件的可行解,然后在这些可行解中找出局部最优解作为全局最优解的候选解.在全局检查步骤中,算法利用SMT求解器MathSAT对每个候选解进行测试,检查其是否为最优解.该算法被集成到基于SMT的优化求解器OPT-MathSAT中.
Li等人[111]研发的SYMBA求解器也可以获取线性实数算术问题的全局最优解,求解步骤主要分为全局推送(GLOBALPUSH)和检测是否无界(UNBOUNDED)2个阶段.在GLOBALPUSH阶段,SYMBA使用Z3判断是否存在1个新的可行解优于当前最优解,如果存在,调整当前最优解的最小下界,如果不存在,则说明当前最优解即为全局最优解.在UNBOUNDED阶段,SYMBA会检测当前最优解是否无界,并调整其最大上界和最小上界.SYMBA会重复这2个阶段直至找到全局最优解为止.
微软研发的νZ[112]可以求解基于SMT公式的线性优化问题.νZ求解线性实数算术问题的方法与OPT-MathSAT的方法类似,区别在于νZ使用SMT求解器MaxSMT求解约束可满足性问题(constraint-satisfaction problem)并利用OptSMT模块优化线性算数目标函数.微软在Z3中也实现了相同的功能.
4.6 基于SMT的其他应用
Arkoudas等人[19]提出了一种访问控制策略自动分析方法.该方法使用可编程定理证明系统Athena实现了策略的框架表示,并把策略转化为SMT公式,调用Athena中的SMT求解接口smt-solve求解公式的可满足性,再对策略进行分析.
Malozemoff等人[113]提出了一种分组密码加密安全性的自动分析与检测方法,该方法首先将加密步骤抽象为含有不同种类节点的有向无环图,图中不同节点代表不同的操作,边代表节点的输入或输出.需要将图中的点和边转化为约束可满足性问题并使用Z3求解问题的可满足性,根据结果判断模式(mode)是有效的(valid)、解密的(decryptable)还是安全的(secure).
李舟军等人[114]对安全漏洞检测技术进行了较为全面的总结,并且介绍了SMT在自动化白盒模糊测试中的应用:首先利用文中提出的轻量级动态符号执行方法获取程序的执行路径,再借助SMT求解器对路径约束求解,用于检测程序的漏洞.
5 结论与展望
SMT以其丰富的背景理论和高效的组合背景理论求解技术成为了可满足性问题求解领域的核心.SMT求解器可以求解含有组合背景理论的一阶逻辑公式,直接处理一些含有高层级信息的可满足问题,成为了许多实际应用的基础.
本文力图详尽地介绍SMT原理、求解方法、工具及最新的应用进展.详细地阐述了SAT,SMT判定算法及理论组合判定算法的实现.根据近11年SMT-COMP竞赛的结果,比较了能够处理大规模工业化应用问题的主流SMT求解器的综合求解能力.从应用的角度阐述了SMT在测试用例自动生成、程序缺陷检测、RTL验证、程序分析与验证以及线性逻辑约束公式优化问题求解等领域中的具体应用.
对于SMT在各个领域中的实际应用而言,还存在着许多新的研究热点和难点.例如,基于有界模型检测的程序缺陷检测受限于界限K,如果想证明程序不违反安全属性要确保:1)程序在界限K内不违反安全属性;2)程序中循环的次数≤K,那么如何验证循环次数远大于K的程序正确性是1个新的研究热点.
基于SAT的门级电路验证会产生状态爆炸问题,将SMT与RTL验证相结合可以很好地缓解这个问题,因此许多学者对此做了相关的研究[10,101],但如何利用SMT验证RTL电路的完全正确性也是未来研究的难点.
对于SMT求解器本身而言,大多数SMT求解器只接受无量词一阶逻辑公式作为输入,实际问题中经常会含有全称量词(∀),求解此类问题是目前SMT求解器的难点之一,仅有少数几个主流的SMT求解器支持带有全称量词问题的求解,比如Z3,CVC4等.求解方法主要分为2种:1)基于模式(pattern-based)的量词实例化方法,主要是将带有全称量词的变量实例化为带有存在量词(∃)的变量,比如将(∀x,x>1)实例化为(∃x=2,x>1).但是如何选取x的具体实例化数值是有待研究的问题.2)基于饱和定理证明(saturation theorem proving),此方法使用了叠加演算的思想解决公式中的量词问题.含有全称量词的一阶逻辑公式可满足性求解算法将是今后的研究热点.
[1]Johnson K, Calinescu R. Efficient re-resolution of SMT specifications for evolving software architectures[C]Proc of the 10th Int ACM Sigsoft Conf on Quality of Software Architectures. New York: ACM, 2014: 93-102
[2]Malik S U R, Khan S U, Srinivasan S K. Modeling and analysis of state-of-the-art VM-based cloud management platforms[J]. IEEE Trans on Cloud Computing, 2013, 1(1): 50-63
[3]Cotrini C, Weghorn T, Basin D, et al. Analyzing first-order role based access control[C]Proc of the 28th IEEE Computer Security Foundations Symp. Piscataway, NJ: IEEE, 2015: 3-17
[4]Arkoudas K, Chadha R, Chiang J. Sophisticated access control via SMT and logical frameworks[J]. ACM Trans on Information and System Security, 2014, 16(4): 1-31
[5]Voss S, Schatz B. Deployment and scheduling synthesis for mixed-critical shared-memory applications[C]Proc of the 20th IEEE Int Conf and Workshops on the Engineering of Computer Based Systems. Piscataway, NJ: IEEE, 2013: 100-109
[6]Huang Yu, Mercer E, Mccarthy J. Proving MCAPI executions are correct using SMT[C]Proc of the 28th IEEE Int Conf on Automated Software Engineerin. Piscataway, NJ: IEEE, 2013: 26-36
[7]Cordeiro L, Fischer B, Marques-Silva J. SMT-based bounded model checking for embedded ANSI-C software[J]. IEEE Trans on Software Engineering, 2012, 38(4): 957-974
[8]Barnat J, Bauch P, Havel V. Model checking parallel programs with inputs[C]Proc of the 22nd Euromicro Int Conf on Parallel, Distributed and Network-Based Processing(PDP). Piscataway, NJ: IEEE, 2014: 756-759
[9]Liu Leyuan, Kong Werqiang, Ando T, et al. A survey of acceleration techniques for SMT-based bounded model checking[C]Proc of 2013 Int Conf on Computer Sciences and Applications (CSA). Piscataway, NJ: IEEE, 2013: 554-559
[10]Kunapareddy S, Turaga S D, Sajjan S S T M. Comparision between LPSAT and SMT for RTL verification[C]Proc of Int Conf on Circuit, Power and Computing Technologies. Piscataway, NJ: IEEE, 2015
[11]Sebastiani R, Tomasi S. Optimization in SMT with LA()cost functions[G]LNAI 7364: Automated Reasoning. Berlin: Springer, 2012: 484-498
[12]Chen Li, Wang Yongji, Wu Jingzheng, et al. Rate-Monotonic optimal design based on tree-like linear programming search[J]. Journal of Software, 2015, 26(12): 3223-3241 (in Chinese)(陈力, 王永吉, 吴敬征, 等. 基于树状线性规划搜索的单调速率优化设计[J]. 软件学报, 2015, 26(12): 3223-3241)
[13]Blackham B, Liffiton M, Heiser G. Trickle: Automated infeasible path detection using all minimal unsatisfiable subsets[C]Proc of Real-Time and Embedded Technology and Applications Symp. Piscataway, NJ: IEEE, 2014: 169-178
[14]Eldib H, Wang Chao, Taha M, et al. Quantitative masking strength: Quantifying the power side-channel resistance of software code[J]. IEEE Trans on Computer-Aided Design of Integrated Circuits and Systems, 2015, 34(10): 1558-1568
[15]Leroy X . Formal verification of a realistic compiler[J]. Communications of the ACM, 2009, 52(7): 107-115
[16]Klein G. Operating system verification—An overview[J]. Sadhana, 2009, 34(1): 27-69
[17]Cook S A. The complexity of theorem-proving procedures[C]Proc of the 3rd Annual ACM Symp on Theory of Computing. New York: ACM, 1971: 151-158
[18]Cousot P, Cousot R, Feret J, et al. The ASTRéE analyzer[G]LNCS 3444: Programming Languages and Systems. Berlin, Springer, 2005: 21-30
[19]Arkoudas K, Loeb S, Chadha R, et al. Automated policy analysis[C]Proc of 2012 IEEE Int Symp on Policies for Distributed Systems and Networks(POLICY). Piscataway, NJ: IEEE, 2012
[20]Nuzzo P, Puggelli A, Seshia S A, et al. CalCS: SMT solving for non-linear convex constraints[C]Proc of the 2010 Conf on Formal Methods in Computer-Aided Design. Piscataway, NJ: IEEE, 2010: 71-80
[21]Chimisliu V, Wotawa F. Category partition method and satisfiability modulo theories for test case generation[C]Proc of the 7th Int Workshop on Automation of Software Test Piscataway, NJ: IEEE, 2012: 64-70
[22]Riener H, Bloem R, Fey G. Test case generation from mutants using model checking techniques[C]Proc of the 4th IEEE Int Conf on Software Testing, Verification and Validation Workshops (ICSTW). Piscataway, NJ: IEEE, 2011: 388-397
[23]JoöBstl E, Weiglhofer M, Aichernig B K, et al. When bdds fail: Conformance testing with symbolic execution and SMT solving[C]Proc of the 3rd Int Conf on Software Testing, Verification and Validation(ICST). Piscataway, NJ: IEEE, 2010: 479-488
[24]Ansótegui C, Bofill M, Manyà F, et al. Building automated theorem provers for infinitely-valued logics with satisfiability modulo theory solvers[C]Proc of the 42nd IEEE Int Symp on Multiple-Valued Logic(ISMVL). Piscataway, NJ: IEEE, 2012: 25-30
[25]Shostak R E. An algorithm for reasoning about equality[J]. Communications of the ACM, 1978, 21(2): 583-585
[26]Shostak R E. Deciding combinations of theories[J]. Journal of the ACM, 1984, 31(1): 209-222
[27]Shostak R E. A practical decision procedure for arithmetic with function symbols[J]. Journal of the ACM, 1979, 26(2): 351-360
[28]Armando A, Giunchiglia E. Embedding complex decision procedures inside an interactive theorem prover[J]. Annals of Mathematics & Artificial Intelligence, 1993, 8(34): 475-502
[29]Armando A, Castellini C, Giunchiglia E. SAT-based procedures for temporal reasoning[G]LNAI 1809: Proc of the 5th European Conf on Planning: Recent Advances in AI Planning. Berlin: Springer, 2000: 97-108
[30]Bryant R E, German S, Velev M N. Exploiting positive equality in a logic of equality with uninterpreted Functions[C]Proc of the 11th Int Conf on Computer Aided Verification. Berlin: Springer, 1999: 470-482
[31]Giunchiglia F, Sebastiani R . Building decision procedures for modal logics from propositional decision procedures: The case study of modalK(m)[J]. Information & Computation, 2000, 162(1): 158-178
[32]Zhang Jian. Specification analysis and test data generation by solving Boolean combinations of numeric constraints[C]Proc of the 1st Asia-Pacific Conf on Quality Software. Piscataway, NJ: IEEE, 2000: 267-274
[33]Malik S, Zhang Lintao. Boolean satisfiability from theoretical hardness to practical success[J]. Communications of the ACM, 2009, 52(8): 76-82
[34]De Moura L, Bjørner N. Z3: An efficient SMT solver[G]LNCS 4936: Tools and Algorithms for the Construction and Analysis of Systems. Berlin: Springer, 2008: 337-340
[35]Barrett C, Deters M, Conway C L, et al. CVC4[G]LNCS 6806: Proc of the 23rd Int Conf on Computer Aided Verification. Berlin: Springer, 2011: 171-177
[36]Dutertre B. Yices2.2[G]LNCS 8559: Proc of the 16th Int Conf on Computer Aided Verification. Berlin: Springer, 2014: 737-744
[37]Bruttomesso R, Cimatti A, Franzén A, et al. The mathsat4 smt solver[G]LNCS 5123: Proc of the 20th Int Conf on Computer Aided Verification. Berlin: Springer, 2008: 299-303
[38]Brummayer R, Biere A. Boolector: An efficient SMT solver for bit-vectors and arrays[G]LNCS 5505: Proc of Tools and Algorithms for the Construction and Analysis of Systems. Berlin: Springer, 2009: 174-177
[39]Godefroid P, De Halleux P, Nori A V, et al. Automating software testing using program analysis[J]. IEEE Software, 2008, 25(5): 30-37
[40]Henzinger T A, Jhala R, Majumdar R, et al. Lazy abstraction[J]. ACM SIGPLAN Notices, 2002, 37(1): 58-70
[41]Wang Jianxin, Guan Lina, Jiang Guohong. A survey of algorithms for SAT problem[J]. Computing Technology and Automation, 2009, 28(4): 138-143 (in Chinese)(王建新, 管利娜, 江国红. 可满足性问题的研究综述[J]. 计算技术与自动化, 2009, 28(4): 138-143)
[42]Sheini H M, Sakallah K A. From propositional satisfiability to satisfiability modulo theories[G]LNCS 4121: Proc of the 9th Int Conf Seattle. Berlin: Springer, 2006
[43]Moura L, Dutertre B, Shankar N. A tutorial on satisfiability modulo yheories[G]LNCS 4590: Proc of the 19th Int Conf on Computer Aided Verification. Berlin: Springer, 2007: 20-36
[44]Jin Jiwei, Ma Feifei, Zhang Jian. Brief introduction to SMT solving[J]. Journal of Frontiers of Computer Science & Technology, 2015, 9(7): 769-780 (in Chinese)(金继伟, 马菲菲, 张健. SMT求解技术简述[J]. 计算机科学与探索, 2015, 9(7): 769-780)
[45]Singer D. Parallel Resolution of the Satisfiability Problem: A Survey[M]. New York: John Wiley & Sons, 2006: 123-148
[46]Hansen P, Jaumard B. Algorithms for the maximum satisfiability problem[J]. Computing, 1990, 44(4): 279-303
[47]Bistarelli S, Montanari U, Rossi F, et al. Semiring-based CSPs and valued CSPs: Frameworks, properties, and comparison[J]. Constraints, 1999, 4(3): 199-240
[48]Mahajan M, Raman V. Parameterizing above guaranteed values: Maxsat and maxcut[J]. Journal of Algorithms, 1999, 31(2): 335-354
[49]Davis M, Putnam H. A computing procedure for quantification theory[J]. Journal of the ACM, 1960, 7(3): 201-215
[50]Davis M, Logemann G, Loveland D. A machine program for theorem-proving[J]. Communications of the ACM, 1962, 5(7): 394-397
[51]Prestwich S. Lynce I: Local search for unsatisfiability[G]LNCS 4121: Proc of Theory and Applications of Satisfiability Testing-SAT 2006. Berlin: Springer, 2006: 283-296
[52]Audemard G, Simon L. GUNSAT: A greedy local search algorithm for unsatisfiability[C]Proc of 2007 Int Joint Conf on Artificial Intelligence. San Francisco: Morgan Kaufmann, 2007: 2256-2261
[53]Xu Daoyun Liu Changyun. DPLL algorithm with literal renaming strategy[J]. Journal of Frontiers of Computer Science & Technology, 2007, 1(1): 116-125 (in Chinese)(许道云, 刘长云. 带文字改名策略的 DPLL 算法[J]. 计算机科学与探索, 2007, 1(1): 116-125)
[54]Nieuwenhuis R, Oliveras A, Rodríguez-Carbonell E, et al. Challenges in satisfiability modulo theories[G]LNCS 4533: Proc of Term Rewriting and Applications. Berlin: Springer, 2007: 2-18
[55]Barrett C, Stump A, Tinelli C. The satisfiability modulo theories library (smt-lib)[EBOL]. 2010[2016-04-03]. http:www.SMT-LIB.org
[56]Mccarthy J. Towards a Mathematical Science of Computation[M]. Berlin: Springer, 1993: 35-56
[57]Barrett C, Tinelli C. Cvc3[G]LNCS 4590: Proc of the 19th Int Conf on Computer Aided Verification. Berlin: Springer, 2007: 298-302
[58]Nelson G, Oppen D C. Simplification by cooperating decision procedures[J]. ACM Trans on Programming Language System, 1979, 1(2): 245-257
[59]Bozzano M, Bruttomesso R, Cimatti A, et al. Efficient satisfiability modulo theories via delayed theory combination[G]LNCS 3676: Proc of Computer Aided Verification. Berlin: Springer, 2005: 335-349
[60]Nelson G, Oppen D C. Fast decision procedures based on congruence closure[J]. Journal of the ACM, 1980, 27(2): 356-364
[61]Huang Zhuo, Zhang Jian. Generating SAT instances from first-order formulas[J]. Journal of Software, 2005, 16(3): 327-335
[62]Seshia S A, Lahiri S K, Bryant R E. A hybrid SAT-based decision procedure for separation logic with uninterpreted functions[C]Proc of the 40th Annual Design Automation Conf. New York: ACM, 2003: 425-430
[63]Bryant R E, Lahiri S K, Seshia S A. Modeling and verifying systems using a logic of counter arithmetic with lambda expressions and uninterpreted functions[G]LNCS 2404: Proc of the 2002 Int Conf on Computer Aided Verification. Berlin: Springer, 2002: 78-92
[64]Pnueli A, Rodeh Y, Shtrichman O, et al. Deciding equality formulas by small domains instantiations[G]LNCS 1633: Proc of the 1999 Int Conf on Computer Aided Verification. Berlin: Springer, 1999: 455-469
[65]Talupur M, Sinha N, Strichman O, et al. Range allocation for separation logic[G]LNCS 3114: Proc of the 2004 Int Conf on Computer Aided Verification. Berlin: Springer, 2004: 148-161
[66]Goel A, Sajid K, Zhou H, et al. BDD based procedures for a theory of equality with uninterpreted functions[C]Proc of the 1998 Int Conf on Computer Aided Verification. Berlin: Springer, 1998: 244-255
[67]Barrett C W, Dill D L, Stump A. Checking satisfiability of first-order formulas by incremental translation to SAT[C]Proc of the 2002 Int Conf on Computer Aided Verification. Berlin: Springer, 2002: 236-249
[68]Wolfman S A, Weld D S. The LPSAT engine & its application to resource planning[C]Proc of the 16th Int Joint Conf on Artificial Intelligence. San Francisco: Morgan Kaufmann, 1999: 310-317
[69]Ball T, Cook B, Lahiri S K, et al. Zapato: Automatic theorem proving for predicate abstraction refinement[G]LNCS 3114: Proc of Computer Aided Verification. Berlin: Springer, 2004: 457-461
[70]Bruno D, Leonardo D M. A fast linear-arithmetic solver for DPLL(T)[G]LNCS 4144: Proc of Computer Aided Verification. Berlin: Springer, 2006: 81-94
[71]Ganzinger H, Hagen G, Nieuwenhuis R, et al. DPLL(T): Fast decision procedures[G]LNCS 3114: Proc of Computer Aided Verification. Berlin: Springer, 2004: 175-188
[72]Bozzano M, Bruttomesso R, Cimatti A, et al. Efficient theory combination via Boolean search[J]. Information and Computation, 2006, 204(10): 1493-1525
[73]Sebastiani R. Lazy satisfiability modulo theories[J]. Journal on Satisfiability, Boolean Modeling and Computation, 2007, 3(9): 141-224
[74]Nieuwenhuis R, Oliveras A, Tinelli C. Solving SAT and SAT modulo theories: From an abstract davis-putnam-logemann-loveland procedure to DPLL (T)[J]. Journal of the ACM, 2006, 53(6): 937-977
[75]Flanagan C, Joshi R, Ou X, et al. Theorem proving using lazy proof explication[G]LNCS 2725: Proc of Computer Aided Verification. Berlin: Springer, 2003: 355-367
[76]Bozzano M, Bruttomesso R, Cimatti A, et al. An incremental and layered procedure for the satisfiability of linear arithmetic logic[G]LNCS 3440: Proc of Tools and Algorithms for the Construction and Analysis of Systems. Berlin: Springer, 2005: 317-333
[77]Jha S, Limaye R, Seshia S A. Beaver: Engineering an efficient smt solver for bit-vector arithmetic[G]LNCS 5643: Proc of Computer Aided Verification. Berlin: Springer, 2009: 668-674
[78]Armando A, Castellini C, Giunchiglia E, et al. A SAT-based decision procedure for the Boolean combination of difference constraints[G]LNCS 3542: Proc of Theory and Applications of Satisfiability Testing. Berlin: Springer, 2005: 16-29
[79]Bofill M, Nieuwenhuis R, Oliveras A, et al. The barcelogic SMT solver[G]LNCS 5123: Proc of the 20th Int Conf on Computer Aided Verification. Berlin: Springer, 2008: 294-298
[80]Bouton T, De Oliveira D C B, Déharbe D, et al. VeriT: An open, trustable and efficient SMT-solver[G]LNAI 5663: Proc of 2009 Int Conf on Automated Deduction. Berlin: Springer, 2009: 151-156
[81]Lahiri S, Qadeer S. Back to the future: Revisiting precise program verification using SMT solvers[J]. ACM SIGPLAN Notices, 2008, 43(1): 171-182
[82]Gulavani B S, Henzinger T A, Kannan Y, et al. SYNERGY: A new algorithm for property checking[C]Proc of the 14th ACM SIGSOFT Int Symp on Foundations of Software Engineering. New York: ACM, 2006: 117-127
[83]Ball T, Rajamani S K. The SLAM project: Debugging system software via static analysis[C]Proc of ACM SIGPLAN Notices. New York: ACM, 2002: 1-3
[84]Costa M, Crowcroft J, Castro M, et al. Vigilante: End-to-end containment of internet worms[C]Proc of 2005 ACM SIGOPS Operating Systems Review. New York: ACM, 2005: 133-147
[85]Godefroid P, Levin M Y, Molnar D. SAGE: Whitebox fuzzing for security testing[J]. Communications of the ACM, 2012, 55(3): 40-44
[86]Anand S, Păsăreanu C S, Visser W. JPF-SE: A symbolic execution extension to Java pathfinder[G]LNCS 4424: Proc of Tools and Algorithms for the Construction and Analysis of Systems. Berlin: Springer, 2007: 134-138
[87]Arcaini P, Gargantini A, Vavassori P. Generating tests for detecting faults in feature models[C]Proc of the 8th IEEE Int Conf on Software Testing, Verification and Validation. Piscataway, NJ: IEEE, 2015
[88]Lin Huimin, Zhang Wenhui. Model checking: Theories, technigues and applications[J]. Acta Electronica Sinica, 2002, 30(12): 1907-1912 (in Chinese)(林惠民, 张文辉. 模型检测: 理论, 方法与应用[J]. 电子学报, 2002, 30(12): 1907-1912)
[89]Ramalho M, Freitas M, Sousa F, et al. SMT-based bounded model checking of C++ programs[C]Proc of the 20th IEEE Int Conf and Workshops on Engineering of Computer Based Systems(ECBS). Piscataway, NJ: IEEE, 2013: 147-156
[90]Cordeiro L. SMT-based bounded model checking of multi-threaded software in embedded systems[C]Proc of the 32nd ACMIEEE Int Conf on Software Engineering. Piscataway, NJ: IEEE, 2011: 373-376
[91]Cordeiro L, Fischer B. Verifying multi-threaded software using smt-based context-bounded model checking[C]Proc of the 33rd Int Conf on Software Engineering. Piscataway, NJ: IEEE, 2011: 331-340
[92]Mueller F. A library implementation of POSIX threads under UNIX[C]Proc of the USENIX Conf. Berkeley, CA: USENIX Association, 1993: 29-42
[93]Pereira P A, Albuquerque H F, Marques H M, et al. Verifying CUDA programs using SMT-based context-bounded model checking[EBOL]. [2016-04-02]. http:svlab.hussamaismail.eti.brpaperssac2016.pdf
[94]Cheng J, Grossman M, Mckercher T. Professional Cuda C Programming[M]. New York: John Wiley & Sons, 2014
[95]Morse J. Expressive and efficient bounded model checking of concurrent software[D]. Southampton: University of Southampton, 2015
[96]Ball T, Rajamani S K. Automatically validating temporal safety properties of interfaces[G]LNCS 2057: Proc of the 8th Int SPIN Workshop on Model Checking of Software. Berlin: Springer, 2001: 103-122
[97]Lingappan L, Ravi S, Jha N K. Satisfiability-based test generation for nonseparable RTL controller-datapath circuits[J]. IEEE Trans on Computer-Aided Design of Integrated Circuits and Systems, 2006, 25(3): 544-557
[98]Duraira V, Kalla P. Exploiting hypergraph partitioning for efficient Boolean satisfiability[C]Proc of the 9th IEEE Int High-Level Design Validation and Test Workshop. Piscataway, NJ: IEEE, 2004: 141-146
[99]Kroening D, Seshia S A. Formal verification at higher levels of abstraction[C]Proc of IEEEACM Int Conf on Computer -Aided Design. Piscataway, NJ: IEEE, 2007: 572-578
[100]Clarke E, Grumberg O, Jha S, et al. Counterexample-guided abstraction refinement[G]LNCS 1855: Proc of Computer Aided Verification. Berlin: Springer, 2000: 154-169
[101]Puri P, Bradley M S H. SI-SMART: Functional test generation for RTL circuits using loop abstraction and learning recurrence relationships[C]Proc of the 33rd IEEE Int Conf on Computer Design. Piscataway, NJ: IEEE, 2015: 38-45
[102]Brady B, Bryant R E, Seshia S, et al. ATLAS: Automatic term-level abstraction of RTL designs[C]Proc of the 8th IEEEACM Int Conf on Formal Methods and Models for Codesign. Piscataway, NJ: IEEE, 2010: 31-40
[103]Zhao Yanni, Bian Jinian, Deng Shujun. Constraints decomposition for RTL verification by SMT[J]. Journal of Computer-Aided Design & Computer Graphics, 2010, 22(2): 234-239 (in Chinese)(赵燕妮, 边计年, 邓澍军. 利用 SMT 约束分解方法求解 RTL 可满足性问题[J]. 计算机辅助设计与图形学学报, 2010, 22(2): 234-239)
[104]Gent K, Hsiao M S. Functional test generation at the RTL using swarm intelligence and bounded model checking[C]Proc of the 22nd Asian Test Symp. Piscataway, NJ: IEEE, 2013: 233-238
[105]Liu L, Vasudevan S. Efficient validation input generation in RTL by hybridized source code analysis[C]Proc of Design, Automation and Test in Europe Conf & Exhibition. Piscataway, NJ: IEEE, 2011
[106]He Yanxiang, Wu Wei, Chen Yong, et al. Path sensitive program verification based on SMT solvers[J]. Journal of Software, 2012, 23(10): 2655-2664 (in Chinese)(何炎祥, 吴伟, 陈勇, 等. 基于SMT求解器的路径敏感程序验证[J]. 软件学报, 2012, 23(10): 2655-2664)
[107]Paganelli G, Ahrendt W. Verifying (in-)stability in floating-point programs by increasing precision, using SMT solving[C]Proc of the 15th Int Symp on Symbolic and Numeric Algorithms for Scientific Computing. Piscataway, NJ: IEEE, 2013: 209-216
[108]Kroening D, Weissenbacher G. Interpolation-based software berification with WOLVERINE[G]LNCS 6806: Proc of the 23rd Int Conf on Computer Aided Verification. Berlin: Springer, 2011: 573-578
[109]Pigorsch F, Scholl C. Lemma localization: A practical method for downsizing SMT-interpolants[C]Proc of the Conf on Design, Automation and Test in Europe. San Jose, CA: EDA Consortium, 2013: 1405-1410
[110]Cohen E, Dahlweid M, Hillebrand M, et al. VCC: A practical system for verifying concurrent C[G]LNCS 5674: Proc of Theorem Proving in Higher Order Logics. Berlin: Springer, 2009: 23-42
[111]Li Yi, Albarghouthi A, Kincaid Z, et al. Symbolic optimization with SMT solvers[C]Proc of the 41st ACM SIGPLAN-SIGACT Symp on Principles of Programming Languages. New York: ACM, 2014: 607-618
[112]Bjørner N, Phan A-D, Fleckenstein L. νZ-an optimizing SMT solver[G]LNCS 9035: Proc of Tools and Algorithms for the Construction and Analysis of Systems. Berlin: Springer, 2015: 194-199
[113]Malozemoff A J, Katz J, Green M D. Automated analysis and synthesis of block-cipher modes of operation[C]Proc of the 27th IEEE Computer Security Foundations Symp. Piscataway, NJ: IEEE, 2014: 140-152
[114]Li Zhoujun, Zhang Junxian, Liao Xiangke, et al. Survey of software vulnerability detection techniques[J]. Chinese Journal of Computers, 2015, 38(4): 717-732 (in Chinese)(李舟军, 张俊贤, 廖湘科, 等. 软件安全漏洞检测技术[J]. 计算机学报, 2015, 38(4): 717-732)

Wang Chong, born in 1991. PhD candidate. Student member of CCF. His main research interests include satisfiability modulo theories, multicore scheduling algorithm, bounded model checking.

Lü Yinrun, born in 1991. PhD candidate. His main research interests include satisfiability modulo theories, optimization algorithm.

Chen Li, born in 1989. PhD candidate. His main research interests include satisfiability modulo theories, real-time system, optimization algorithm.

Wang Xiuli, born in 1997. Associate professor and PhD supervisor. His main research interests include information security and game theory.

Wang Yongji, born in 1962. Professor and PhD supervisor. Senior member of CCF. He is the winner of the 2002 One-Hundred-Talent People Program sponsored by the Chinese Academy of Sciences. His main research interests include computer-controlled real-time systems, network optimization theory, intelligent software engineering, nonlinear optimization theory, real-time hybrid control theory, real-time embedded operating system, etc.
Survey on Development of Solving Methods and State-of-the-Art Applications of Satisfiability Modulo Theories
Wang Chong1,2,3, Lü Yinrun1,2,3, Chen Li1,2,3, Wang Xiuli4, and Wang Yongji1,3
1(NationalEngineeringResearchCenterforFundamentalSoftware(InstituteofSoftware,ChineseAcademyofSciences),Beijing100190)2(UniversityofChineseAcademyofSciences,Beijing100049)3(StateKeyLaboratoryofComputerScience(InstituteofSoftware,ChineseAcademyofSciences),Beijing100190)4(SchoolofInformation,CentralUniversityofFinanceandEconomics,Beijing100081)
The satisfiability modulo theories (SMT) problem is a decision problem for the satisfiability of first-order logical formula with respect to combinations of background theories. SMT supports many background theories, so it can describe a lot of practical problems in industrial fields or academic circles. Also, the expression ability and the efficiency of decision algorithms of SMT are both better than those of SAT (satisfiability). With its efficient satisfiability decision algorithms, SMT has been widely used in many fields, in particular in test-case generation, program defect detection, register transfer level (RTL) verification, program analysis and verification, solving linear optimization over arithmetic constraint formula, etc. In this paper, we firstly summarize fundamental problems and decision procedures of SAT. After that, we give a brief overview of SMT, including its fundamental concepts and decision algorithms. Then we detail different types of decision algorithms, including eager and lazy algorithms which have been studied in the past five years. Moreover, some state-of-the-art SMT solvers, including Z3, Yices2 and CVC4 are analyzed and compared based on the results of the SMT’s competition. Additionally, we also focus on the introduction for the application of SMT solving in some typical communities. At last, we give a preliminary prospect on the research focus and the research trends of SMT.
satisfiability modulo theories (SMT); SMT solver; decision algorithms of SMT; test-case generation; program defect detection; cloud computing
2016-04-26;
2016-07-14
国家自然科学基金项目(61170072,61303057);中国科学院、国家外国专家局创新团队国际合作伙伴计划 This work was supported by the National Natural Science Foundation of China (61170072,61303057) and the CASSAFEA International Partnership Program for Creative Research Teams.
王永吉(ywang@itechs.iscas.ac.cn)
TP301
