供应中断下第三方物流安全性网络设计模型与算法

李 锐 孙福明

(辽宁工业大学电子与信息工程学院 辽宁 锦州 121001)



供应中断下第三方物流安全性网络设计模型与算法

李 锐 孙福明

(辽宁工业大学电子与信息工程学院 辽宁 锦州 121001)

物流网络是第三方物流(3PL)运作的基础，对3PL的有效运作起到重要作用。事实上，3PL服务网络会受到各种因素的影响而发生供应中断。为了使3PL能够提供安全、有效的物流服务，研究3PL安全性网络设计问题。建立3PL安全性网络设计优化模型，在满足供应中断水平约束的条件下，最小化物流总成本。根据问题模型的NP-hard特点，设计差分进化(DE)算法进行求解。最后，通过仿真实验对模型和算法进行测试，仿真实验结果表明模型具有合理性，并且DE算法能够对问题有效求解。

第三方物流 网络设计 供应中断 安全性 差分进化

0 引 言

随着市场竞争的日益加剧，企业开始意识到物流管理是控制成本的有效途径。然而，由于管理技术和专业能力的不足，企业很难发展自己的物流系统。因此，许多企业为了提高市场竞争力，逐渐将物流业务外包给专业的第三方物流(3PL)公司，进而集中优势来发展自己的核心业务。3PL是指在物流业务外包的基础上，由专业的物流服务企业以契约或合同的方式对有物流需求的企业提供物流服务的一种运作方式[1]。

物流网络是物流系统运作的基础，所以设计一个高效的物流服务网络是3PL管理者必须考虑的问题。目前，国内外学者已经对3PL网络设计问题进行了一定的研究。高阳等[2]研究考虑多运营周期情况下的3PL多目标回收物流网络设计问题。何波等[3]对基于3PL的回收网络设计问题的模型及算法进行了研究。KO等[4]基于混合优化仿真方法研究3PL配送网络设计问题。KO等[5]研究多周期的3PL正逆向集成网络设计问题，并设计遗传算法进行求解。Min等[6]则对多周期下的3PL的逆向物流网络设计问题进行了研究。Mahmoudzadeh等[7]对用于伊朗报废车辆回收的3PL逆向网络设计问题进行了研究。Baligil等[8]研究了3PL配送网络优化问题，并设计两阶段的求解方法。Suyabatmaz等[9]基于一种混合仿真分析建模方法研究3PL逆向网络设计问题。

值得注意的是，以上关于3PL网络设计问题的研究并没有考虑安全性。现实中，3PL物流设施和运输线路会受到火灾、飓风、泥石流、恐怖袭击等各种自然或人为因素的影响而发生供应中断，进而影响3PL网络的正常运作。因此，设计一个安全的3PL服务网络具有现实意义。最近，考虑安全性的物流网络设计问题成为研究热点[10-13]。目前，考虑供应中断的3PL安全性网络设计问题还没有得到关注。

本文研究供应中断下3PL安全性网络设计问题。与已有3PL网络设计问题不同，在3PL网络设计的同时考虑供应中断的发生，建立带有供应中断水平约束的3PL网络设计优化模型，根据模型NP-hard特性设计差分进化算法进行求解。最后，通过仿真实验对模型的合理性和算法的有效性进行验证。

1 问题描述及模型

考虑3PL承担某一区域内的物流配送任务。如图1所示，3PL网络由供应点、需求点、3PL仓库、3PL物流中心和运输线路组成，并且采用单源供应网络结构[10]，即每个物流节点都由单一的上级节点来供应。

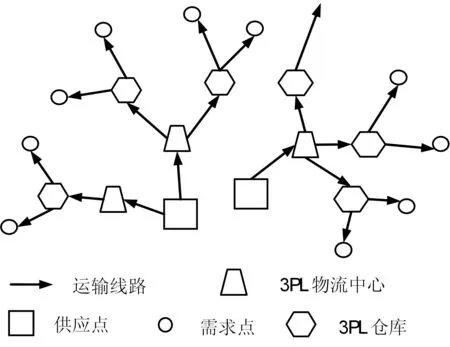
图1 3PL网络结构

由于自然或人为因素的影响，供应点、3PL物流中心、3PL仓库可能发生供应中断。安全性描述3PL服务网络对供应中断的抵御能力，具体来说是指3PL网络的供应点、3PL物流中心、3PL仓库在发生供应中断的情况下其供应产品的损失比率不超过一定的水平。

供应中断下3PL安全性网络设计问题是指通过选择开设3PL物流中心和3PL仓库来构建3PL服务网络，最小化物流总成本，同时使网络满足供应中断水平要求。

1.1 符号说明

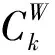
1.2 决策变量定义

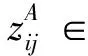
1.3 优化模型

基于以上符号说明和变量定义，建立供应中断下3PL安全性网络设计优化模型如下：

(1)

s.t.

(2)

(3)

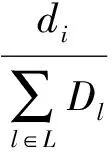
(4)

(5)

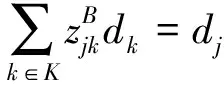
(6)

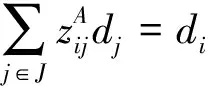
(7)

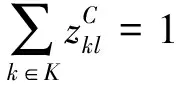
(8)

(9)

(10)

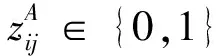
(11)

(12)

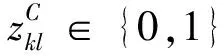
(13)

xj∈{0,1} ∀j∈J

(14)

yk∈{0,1} ∀k∈K

(15)

目标函数式(1)最小化物流总成本，包括3PL物流中心、3PL仓库、运输线路的开设成本，以及产品的运输处理成本；式(2)、式(3)和式(4)分别为3PL仓库、3PL物流中心和供应点的供应中断水平约束，即要求3PL仓库、3PL物流中心和供应点在发生供应中断的情况下，其供应产品的损失比率不超过要求的水平β1、β2和β3，变量dk、dj和di分别为3PL仓库、3PL物流中心和供应点的产品流通量；式(5)、式(6)和式(7)分别为3PL仓库、3PL物流中心和供应点的产品流通量约束；式(8)-式(10)分别为需求点、3PL仓库、3PL物流中心的单源供应约束；式(11)-式(15)表示二值的决策变量。

2 差分进化算法

供应中断下3PL安全性网络设计问题是经典NP-hard问题——固定费用网络设计问题——的扩展，因此也属于NP-hard问题，所以智能优化方法更适合对该问题进行求解。

差分进化DE(Differential Evolution)算法是由Storn等[15]提出的一种基于群的随机搜索算法。DE利用变异、交叉操作产生新种群，通过选择操作保存优秀个体，通过反复迭代，实现不断进化。目前，DE算法已经在各个领域得到了应用，如炼钢-连铸生产调度问题[16]、多目标优化问题[17]、任务调度问题[18]、复杂网络社区发现问题[19]等，并且算法性能也已得到了验证。

此外，标准DE算法的个体采用实数编码方式，能够很好地解决问题模型中各决策变量之间的相互关系和约束条件的限制。因此，本文设计DE算法对问题进行求解。其中，供应中断水平约束作为惩罚项加入到个体评价函数中进行处理，而按照本文所设计的个体编码方式，模型中的其他约束则可自动满足。

2.1 DE算法的总体步骤

DE算法的主要步骤如下：

Step1根据2.2节的个体编码方式随机产生初始种群。

Step2对当前种群的每个个体Xi(t)，i=1,2,…,N按式(16)产生对应的变异个体：

Vi(t+1)=Xr1(t)+F×(Xr2(t)-Xr3(t))

(16)

其中Xr1(t)、Xr2(t)、Xr3(t)表示种群中随机选取的互不相同的个体，且不同于个体Xi(t)，F为缩放因子，用于控制差向量的大小，t表示当前代数。

Step3将目标个体Xi(t)与变异操作产生的扰动个体Vi(t+1)按照式(17)进行交叉，生成新的实验个体：

(17)

其中rand表示[0,1]之间的随机数，CR∈[0,1]为交叉概率。

Step4对个体Ui(t+1)和Xi(t)进行评价(详见2.3节)，并按式(18)选择较优的个体作为子代个体：

(18)

其中f1和f2分别为和Xi(t)所对应的评价函数值。

Step5如果算法达到最大循环代数，则转到Step6；否则，转到Step2。

Step6选择目标值最小的解输出。

2.2 个体的编码与解码

如图2所示，个体(问题的解)由实数向量表示。向量由需求节点、3PL仓库和3PL物流中心三个部分组成。向量的维数是所有需求节点、3PL仓库和3PL物流中心的数量之和。向量每一位的取值表示对应节点的上一级节点的选择情况。其中，需求节点部分每一位的取值范围为[1,nK]，nK表示3PL仓库数量；3PL仓库部分每一位的取值范围为[1,nJ]，nJ表示3PL物流中心数量；3PL物流中心部分每一位的取值范围为[1,nS]，nS表示供应点数量。例如，需求节点部分某一位的取值为“2.3”，四舍五入取整为“2”，表示对应的需求节点由3PL仓库“2”提供服务。

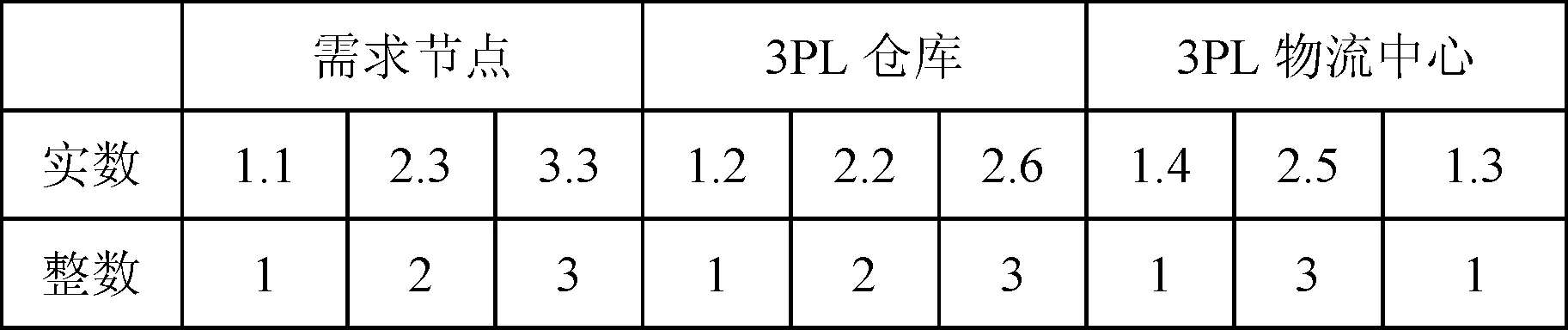
图2 个体向量的表示

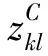
2.3 个体的评价

对个体进行解码得到解(X,Y)，然而一个解还可能不满足供应中断水平约束式(2)、式(3)和式(4)，将其作为惩罚项加入评价函数中，按式(19)计算个体的适应值：

(19)

其中C(X,Y)表示目标函数式(1)；λ1、λ2和λ3分别为供应中断水平约束式(2)、式(3)和式(4)的惩罚系数；(·)+表示：如果括号内为正数，则取该值。

3 实验及结果分析

为了测试DE算法的有效性，对数据随机生成的算例进行仿真实验。算法采用Matlab语言编程，实验环境为Intel Core 2 CPU 1.83 GHz，内存2.00 GB。

3.1 实验算例

表1 算例的规模

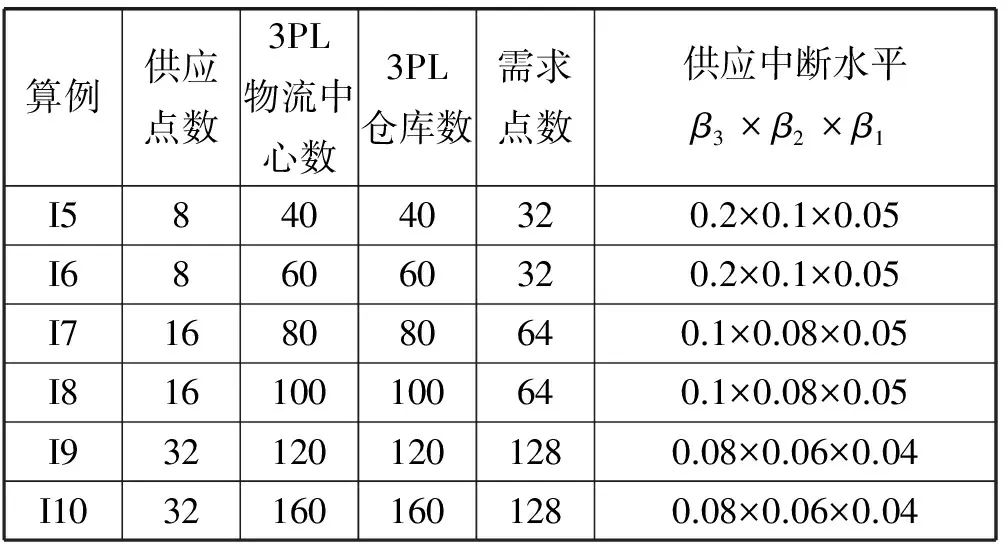
续表1

3.2 结果及分析

首先对不同规模的算例进行求解来测试DE算法的性能。DE算法的参数设置如下：种群规模为30，循环代数为500，交叉概率CR为0.1，缩放因子F为0.3。对于每个算例算法分别运行20次，表2给出最好值、最差值、平均值、平均偏差率(((平均值-最好值)/最好值)×100%)、标准方差百分比((标准方差/平均值)×100%)和平均运行时间。由表2可见，随着算例规模的增大，平均偏差率在1%～7%范围内变化，标准方差百分比保持在1%～4%之间。可见，随着算例规模的增大，DE算法仍然能够保持稳定的性能。表3给出算例I1-I10的详细结果，包括目标值、物流节点开设成本、运输线路开设成本、运输和处理成本。

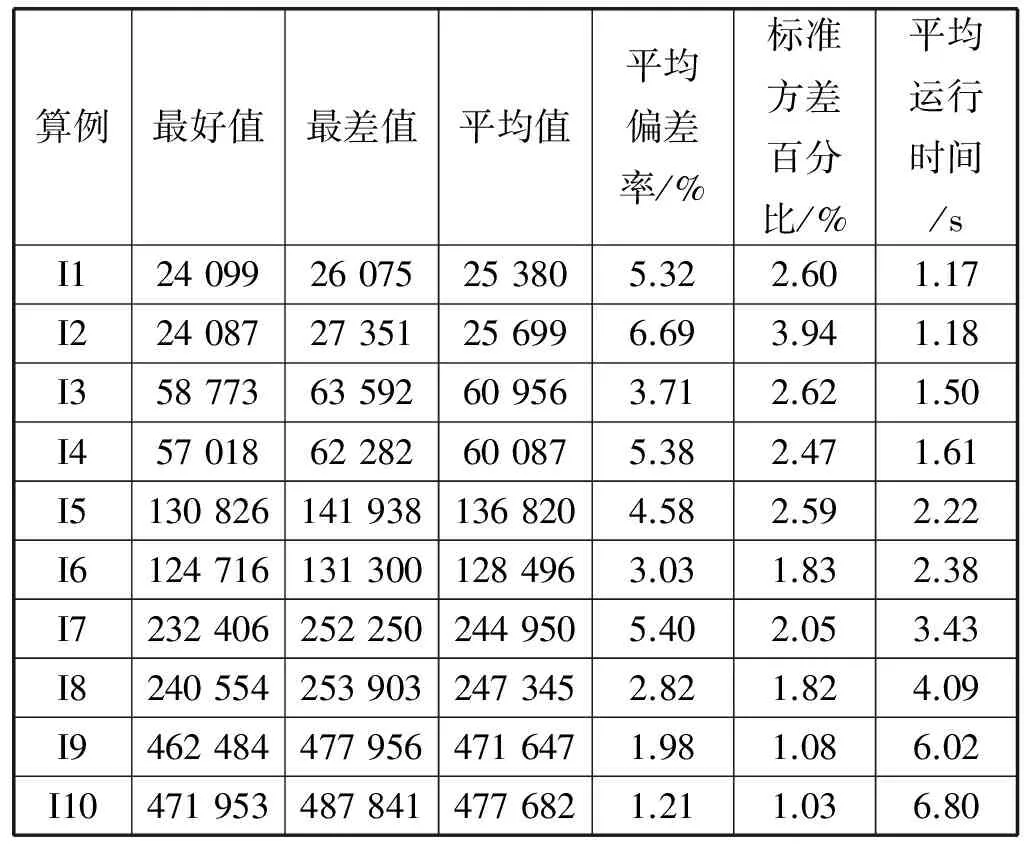
表2 不同规模算例下DE算法的求解结果

续表3

为了分析供应中断水平β1、β2和β3对算例结果的影响，分别以算例I5和I10为例进行实验。表4给出不同供应中断水平下，算例I5和I10的详细结果。由表4可见，随着β1、β2和β3值的减小，算例I5和I10的目标值、物流节点和运输线路的开设成本、运输和处理成本整体上都呈现增加的趋势。可见，要得到对供应中断抵御能力较强的网络，即安全性较好的网络，需要投入更多成本来构建更多的3PL仓库、3PL物流中心和运输线路，分散供应源，进而减小供应中断所导致的供应产品损失。

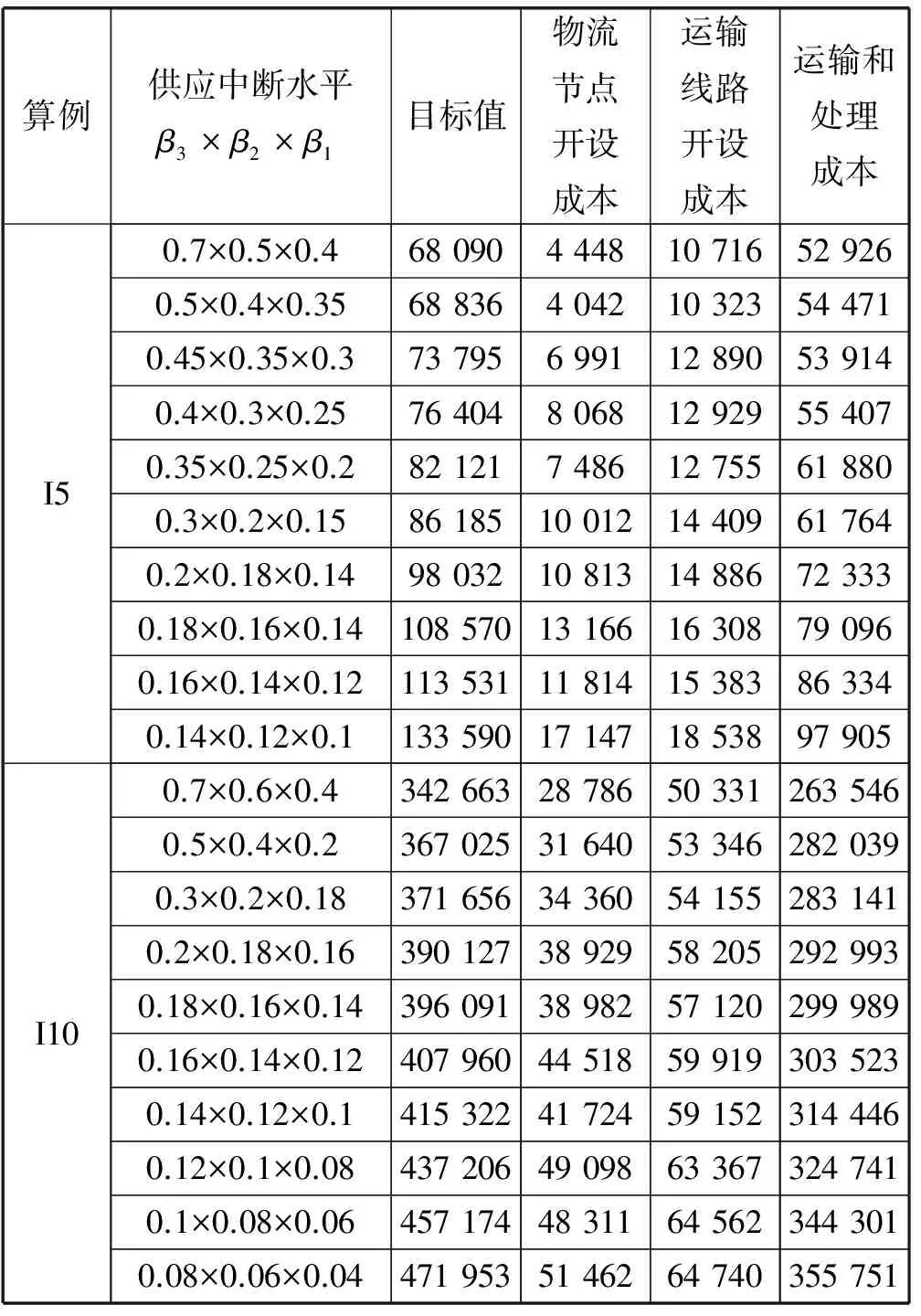
表4 不同供应中断水平下算例I5和I10的详细结果

为了分析DE算法的两个重要参数交叉概率CR和缩放因子F对算法性能的影响，以算例I1为例进行实验。其中，CR和F的取值范围分别为0.1～0.9之间。图3给出不同交叉概率CR取值下，平均偏差率随缩放因子F的变化曲线。由图3可见，交叉概率取值为0.1，缩放因子取值在0.1～0.5之间，算法能够获得较优的性能。

图3 交叉概率和缩放因子对算法性能的影响

4 结 语

研究了供应中断下第三方物流安全性网络设计问题，使3PL服务网络具有抵御供应中断的能力。建立了带有供应中断水平约束的3PL网络设计优化模型。由于问题模型NP难的特点，设计差分进化算法进行求解。最后，通过仿真实验对模型的合理性及算法的有效性进行了验证，仿真实验结果表明模型能够对供应中断下的3PL安全性网络设计问题进行合理描述，并且DE算法能够对问题进行有效求解。此外，分析了供应中断水平对网络设计中各种成本的影响，结果表明要得到安全性较好的网络需要增加成本。

[1] Marasco A.Third-party logistics:a literature review[J].International Journal of Production Economics,2008,113(1):127-147.

[2] 高阳,詹沙磊.基于第三方物流的多周期多目标产品回收网络设计[J].控制与决策,2010,25(8):1164-1168.

[3] 何波,杨超,任鸣鸣.基于第三方物流的产品回收物流网络优化模型及算法[J].计算机集成制造系统,2008,14(1):39-44.

[4] Ko H J,Ko C S,Kim T.A hybrid optimization/simulation approach for a distribution network design of 3PLS[J].Computers & Industrial Engineering,2006,50(4):440-449.

[5] Ko H J,Evans G W.A genetic algorithm-based heuristic for the dynamic integrated forward/reverse logistics network for 3PLs[J].Computers and Operations Research,2007,34(2):346-366.

[6] Min H,Ko H J.The dynamic design of a reverse logistics network from the perspective of third-party logistics service providers[J].International Journal of Production Economics,2008,113(1):176-192.

[7] Mahmoudzadeh M,Mansour S,Karimi B.To develop a third-party reverse logistics network for end-of-life vehicles in Iran[J].Resources,Conservation and Recycling,2013,78:1-14.

[9] Suyabatmaz A Ç,Altekin F T,ahin G.Hybrid simulation-analytical modeling approaches for the reverse logistics network design of a third-party logistics provider[J].Computers & Industrial Engineering,2014,70:74-89.

[10] Peng P,Snyder L V,Lim A,et al.Reliable logistics networks design with facility disruptions[J].Transportation Research Part B,2011,45(8):1190-1211.

[11] Meepetchdee Y,Shah N.Logistical network design with robustness and complexity considerations[J].International Journal of Physical Distribution & Logistics Management,2007,37(3):201-222.

[12] Vahdani B,Tavakkoli-moghaddam R,Modarres M,et al.Reliable design of a forward/reverse logistics network under uncertainty:a robust-M/M/c queuing model[J].Transportation Research Part E:Logistics and Transportation Review,2012,48(6):1152-1168.

[13] Hatefi S M,Jolai F.Reliable forward-reverse logistics network design under partial and complete facility disruptions[J].International Journal of Logistics Systems and Management,2015,20(3):370-394.

[15] Storn R,Price K.Differential evolution-a simple and efficient heuristic for global optimization over continuous spaces[J].Journal of Global Optimization,1997,11(4):341-359.

[16] Tang L,Zhao Y,Liu J.An improved differential evolution algorithm for practical dynamic scheduling in steelmak-ing-continuous casting production[J].IEEE Transactions on Evolutionary Computation,2014,18(2):209-225.

[17] 刘红平,黎福海.面向多目标优化问题的自适应差分进化算法[J].计算机应用与软件,2015,32(12):249-252.

[18] 董丽丽,黄贲,介军.云计算中基于差分进化算法的任务调度研究[J].计算机工程与应用,2014,50(5):90-95.

[19] 张英杰,龚中汉,陈乾坤.基于免疫离散差分进化算法的复杂网络社区发现[J].自动化学报,2015,41(4):749-757.

MODELANDALGORITHMSAFETYNETWORKDESIGNOFTHIRD-PARTYLOGISTICSUNDERSUPPLYDISRUPTIONS

Li Rui Sun Fuming
(CollegeofElectronicandInformationEngineering,LiaoningUniversityofTechnology,Jinzhou121001,Liaoning,China)

As the operation basis of the third party logistics (3PL), the logistics network plays an important role in the efficient operation of 3PL. In reality, supply disruption may happen in 3PL service network due to the influence of various factors. In order to offer secure and efficient logistics service, we study the design problem of 3PL safety network. Therefore, an optimization model of 3PL safety network design was established, which minimized the total logistics costs subjective to the constraints of supply disruption level. And according to the NP-hard characteristic of model, a differential evolution (DE) algorithm was developed. Through simulation experiment, the proposed model and algorithm are reasonable and the DE can solve the problem effectively.

Third party logistics Network design Supply disruption Safety Differential evolution

2016-11-17。国家自然科学基金项目(61572244)；辽宁省教育厅科学研究一般项目(L2015232)。李锐，讲师，主研领域：物流优化，智能计算。孙福明，教授。

TP29

A

10.3969/j.issn.1000-386x.2017.08.006