基于SVD —形态降噪的TKEO故障诊断方法研究*
2017-08-09黄刚劲范玉刚
黄刚劲, 范玉刚, 冯 早, 齐 鹏
(1.昆明理工大学 信息工程与自动化学院,云南 昆明 650500;2.云南省矿物管道输送工程技术研究中心,云南 昆明 650500)
基于SVD—形态降噪的TKEO故障诊断方法研究*
黄刚劲1,2, 范玉刚1,2, 冯 早1,2, 齐 鹏1,2
(1.昆明理工大学 信息工程与自动化学院,云南 昆明 650500;2.云南省矿物管道输送工程技术研究中心,云南 昆明 650500)
针对强噪声干扰背景下微弱故障特征信息难以提取的问题,提出了一种基于奇异值分解(SVD)—形态降噪的Teager能量算子(TKEO)故障诊断方法。首先对轴承振动信号进行SVD,对得到的分量信号进行形态滤波,以滤除噪声干扰;然后利用峭度准则对分量信号进行筛选,并对其进行重构;最后利用TKEO计算重构信号的瞬时能量,得到信号的能量谱,提取振动信号的特征。将提出的方法应用于滚动轴承故障分析,结果表明该方法能清晰地提取故障特征信息。
奇异值分解; 形态学滤波; 峭度准则; Teager能量算子; 故障诊断
0 引 言
滚动轴承是旋转机械中最容易发生故障的一个部件,其运行状态往往直接影响整机的性能,因此对其进行故障监测和诊断的研究有着重要意义[1]。由于轴承在运行过程中难免会受到外界环境的噪声干扰,其早期微弱故障特征的冲击特征往往会被淹没而不易被发现。如何在强噪声背景下有效提取轴承的微弱故障特征信息,对滚动轴承进行故障监测与诊断成为该领域研究的一个热点[2]。
由于奇异值分解(singular value decomposition,SVD)是一种代数特征提取方法,具有良好的数值稳健性,被广泛应用于故障诊断等领域[3]。目前,SVD主要用于信号的降噪[3]、信号的特征提取[4]和奇异谱分析[5]等。文献[3]利用基于差分谱的SVD方法对车削力信号进行降噪处理,但滤除的主要是随机噪声,对脉冲噪声滤除效果不明显,影响故障特征信息的有效提取。形态学滤波器能够在强噪声背景下抑制脉冲干扰,并且保留信号的冲击特征。该算法针对信号的形态特征对信号进行处理,具有算法简单、运算量小等优点[6]。文献[7]先对信号进行SVD,然后对其形态学滤波,分别剔除随机噪声和脉冲噪声,但文中没有考虑噪声对SVD分量的影响。 针对上述问题,本文提出了基于SVD—形态降噪的Teager能量算子(Teager-Kaiser energy operator,TKEO)故障诊断方法,提取轴承故障信号的特征频率,进行故障检测。首先,通过奇异值贡献率确定分解维数,对故障信号构造Hankel矩阵进行奇异值分解,对得到的分量信号通过形态学滤波器进行滤波,以滤除噪声干扰;然后,利用峭度准则对分量信号进行筛选,并对其进行重构;最后,通过TKEO计算重构信号的瞬时能量,得到故障信号的能量频谱,从而有效地提取故障特征信息,判断故障类型。
1 SVD分量形态降噪
SVD是指[3]:对于一个实矩阵A∈Rm×n,不管其行列是否相关,必定存在正交矩U∈Rm×m,V∈Rn×n,使得
A=USVT
(1)
成立,其中S=[diag(σ1,σ2,…,σk)0]或者其转置,取决于m≤n还是m>n,S∈Rm×n。0为零矩阵x,k=min(m,n),且有σ1≥σ2≥…≥σk>0,称为A的奇异值。
1.1 构建Hankel矩阵与维数确定
将SVD应用于处理信号必须构造合适的矩阵A。常用构造矩阵的方法包括Hankel矩阵、Toeplitz矩阵、Cycle矩阵等,研究表明,使用Hankel矩阵构建分析矩阵,SVD可以有效去除振动信号中噪声成份[8]。因此,为了在强噪声背景下提取出微弱故障特征信息,本文采用Hankel矩阵进行SVD。
假定某含噪声信号为X=[x1,x2,… ,xn],使用此信号构造Hankel矩阵如下
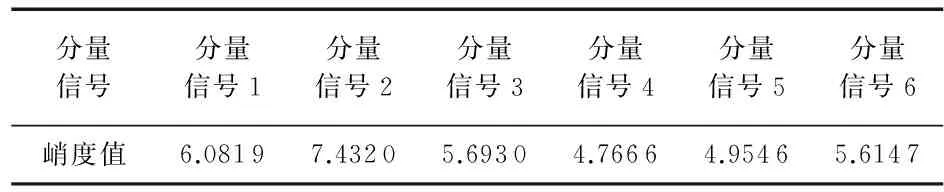
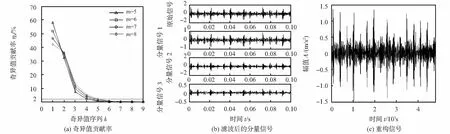
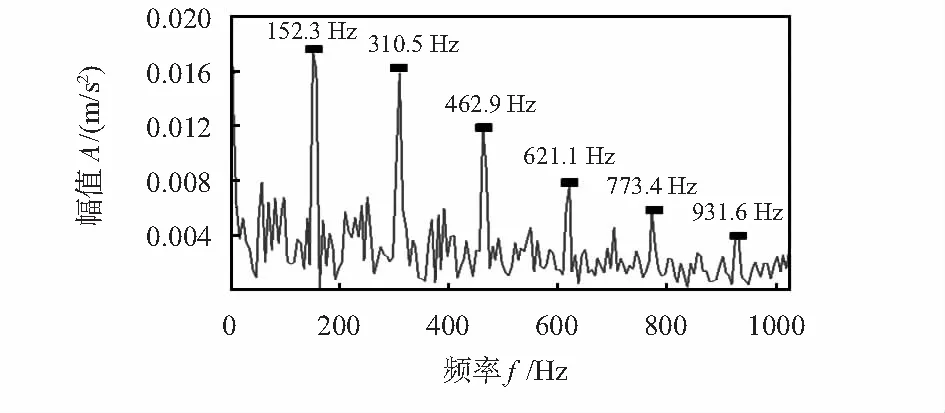
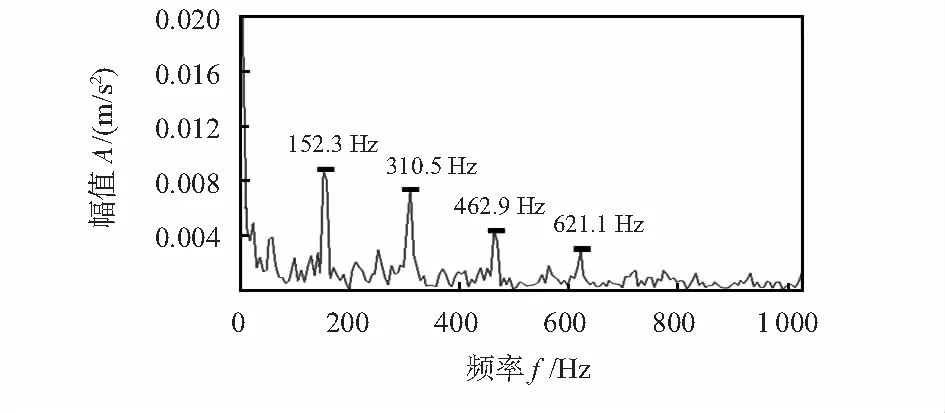
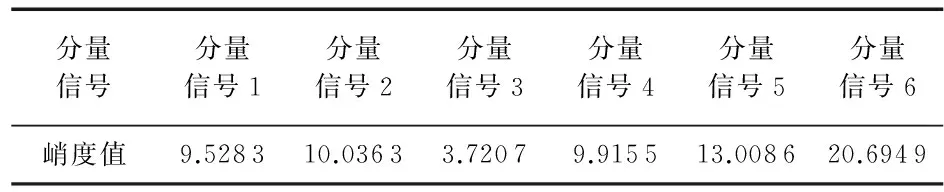
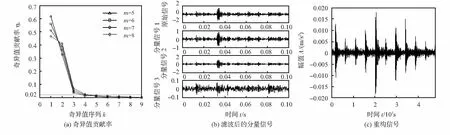
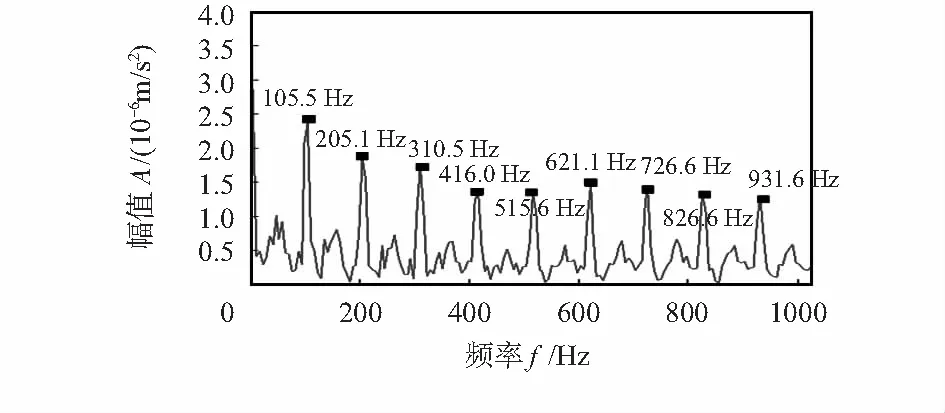
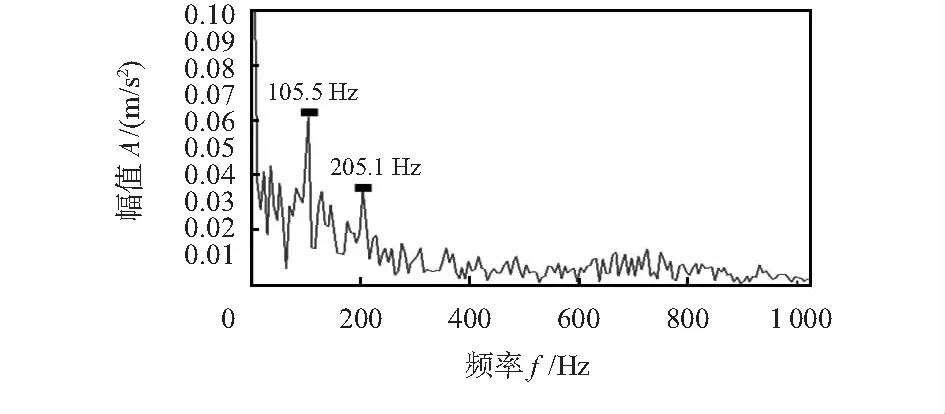
式中 1 1.2 形态学滤波器及结构元素的选择 形态学滤波是一种非线性的滤波方法,利用预先定义的结构元素作为探针,对信号进行探测,以达到保存原信号的形状特征和抑制脉冲干扰的作用。形态学滤波器包括膨胀、腐蚀、开、闭4种基本运算[6]。 设时间序列信号f(n)和一维结构元素序列g(n)的定义域分别为Df={0,1,2,...,N-1}和Dg={0,1,2,...,M-1},其中N和M分别为f(n)和g(n)的长度,且N>M。 1)膨胀运算f(n) (f⊕g)(n)=max[f(n-m)+g(n)],m∈Dg (2) 2)腐蚀运算 (fΘg)(n)=max[f(n-m)+g(m)],m∈Dg (3) 3)开运算 (f°g)(n)=(fΘg⊕g)(n) (4) 4)闭运算 (f·g)(n)=(f⊕gΘg)(n) (5) 其中,形态开运算可去除信号边缘的毛刺,滤除信号上方的峰值噪声;形态闭运算用于填补信号的漏洞和裂纹,平滑信号下方的波谷噪声。为了同时滤除正负脉冲噪声,采用形态开—闭和闭—开组合形态滤波器,定义如下 Foc(f(n))=(f°g·g)(n) (6) Fco(f(n))=(f·g°g)(n) (7) 由于开—闭和闭—开滤波器虽然可同时滤除信号中的正负脉冲,但因开运算的收敛性导致开—闭滤波器的输出偏小,闭运算的扩张性导致闭—开滤波器的输出偏大,存在统计偏倚现象。为了有效地抑制噪声的干扰,采用开—闭和闭—开运算级联的方式来组合滤波器,即 y(n)=[Foc(f(n))+Fco(f(n))]/2 (8) 形态滤波的效果不仅取决于变化形式还取决于结构元素。考虑到滚动轴承故障信号的特点,为了有效地滤除脉冲干扰,本文选用的是半圆型结构元素,文献[10]认为半圆型结构元素适合用于滤除滚动轴承故障信号中的脉冲噪声干扰。 1.3 峭 度 峭度[11]用于反映振动信号分布的数值统计量,其值大小可用于分析振动信号中所包含冲击成份的多少,数学描述如下 (9) 式中μ为信号x的均值;σ为信号x的标准方差。 峭度作为无量纲参数,对冲击信号十分敏感,特别适合轴承表面损伤类故障诊断。峭度值越大,说明信号中的冲击成份所占的比例越重,故障冲击成份越明显,故障信息越容易提取[12]。 对于任意连续信号x(t),TKEO表达式为 (10) 而对于离散信号x(n),可用离散差分方程代替连续时间量的导数,得离散信号x(n)的TKEO表达式如下 ψd[x(n)]=x2(n)-x(n-1)x(n+1) (11) 由于TKEO在分析信号瞬时变化具有良好的自适应能力,能有效地提取故障信号的瞬时频率和瞬时幅值[13]。因此,本文将其用于计算轴承故障信息的瞬时能量,此方法可凸显故障冲击特征,有利于故障信息的有效提取。 根据上述理论分析,本文提出了基于SVD—形态降噪的TKEO故障诊断方法。该方法首先对轴承故障信号进行奇异值分解,对得到的分量信号进行形态滤波;然后利用峭度准则选取峭度值最大和次大的分量信号进行重构[12];最后通过TKEO计算重构信号的瞬时能量,得到故障信号的能量谱,提取故障信号的特征频率,判断故障类型。 具体步骤如下: 1)对轴承故障信号以固定的采样频率进行采样。 2)对采集到的轴承故障信号X构建m=2的Hankel矩阵A,对其进行SVD分析,得奇异值矩阵S1=[diag(σ1,…,σm-1) 0],并求解奇异值贡献率N1=[η1,…,ηm-1]。 3)令m=m+1,重复执行步骤(1),得奇异值贡献率Nm-1,若Nk~Nm-1中总有ηk小于某一特定值η(本文取η=2 %),则循环结束,并由此确定m=k;否则,重复执行本步骤,直至满足循环结束条件。 4)对已确定维数的分析矩阵进行SVD分解,对得到的分量信号进行形态学滤波,以滤除信号中的噪声干扰;通过峭度准则选取峭度值最大和次大的分量信号进行重构。 5)通过TKEO计算重构信号的瞬时能量,并对其进行频谱分析,提取故障特征信息。 6)根据能量谱特征得出诊断结果。 4.1 实验应用 为了进一步验证本文提出的方法对滚动轴承故障特征信息提取的有效性,采用来自美国凯斯西储大学电气工程实验室的数据[14]对轴承的外圈和内圈进行分析。实验采用的轴承型号为6205—2RSJEMSKF,滚动体径7.94mm,滚动轴承节径39.04mm,滚动体个数为9个,接触角为0°,轴承负载2.237kW,转频1 730r/min,采样频率为48kHz,采用长度为4 800点。在轴承内圈、外圈上各加工直径为0.177 8mm,深0.279 4mm的小槽模拟轴承内圈、外圈局部裂纹故障。 根据轴承特征振动理论,计算得轴承内圈故障基频fi=156.14Hz;外圈故障基频fo=103.36Hz。 4.2 实验分析 应用本文的方法对轴承内圈进行故障诊断。根据奇异值贡献率确定Hankel矩阵维数,曲线如图1(a)所示,由图可以看出:当维数大于6时,奇异值均趋近于零,其贡献率小于本文所设阈值(2 %),由此确定m=6作为构建SVD分析矩阵的维数。SVD分解得到6个分量信号,将其进行形态学滤波,滤波后的分量信号的波形如图1(b)所示(受篇幅限制,本文仅给出前3个分量信号的图形),由图可以看出通过形态滤波后的分量信号,基本上消除了脉冲干扰,保留信号的冲击特征。滤波后的6个分量信号的峭度值如表1所示,选取峭度最大分量信号(分量信号1,峭度值为7.432)和次大分量(分量信号6,峭度值为6.081 9)进行信号重构,重构信号如图1(c)所示,可以看出冲击成份特别明显,适合用于作为故障特征信号的提取。通过TKEO计算重构后的瞬时能量,进而对其进行频谱分析,其能量谱如图2所示,图中清晰定位到了内圈故障的基频152.3Hz(与理论故障频率156.14Hz接近),倍频可有效定位到6倍频,因此可准确判断轴承处于内圈故障状态。将本文方法与文献[3]中采用的方法进行对比,文献[3]内圈特征提取结果如图3所示。可以看出,虽然能提取到基频,但其幅值较小且高频处没有明显的故障特征频率。 表1 内圈故障分量信号的峭度指标 图1 内圈故障信号的SVD分析结果 图2 本文方法TKEO能量频谱 图3 文献[3]内圈特征提取结果 应用本文方法对轴承外圈进行故障诊断。根据奇异值贡献率确定Hankel矩阵维数,其曲线如图4(a)所示,由图可以看出当维数大于6时,奇异值均趋近于零,其贡献率小于本文所设阈值(2 %),由此确定m=6作为构建SVD分析矩阵的维数。SVD分解得到6分量信号,将其进行形态滤波,滤波后的分量信号波形如图4(b)所示(篇幅限制,仅给出前3个分量信号的图形),由图可以看出通过形态滤波后的分量信号,基本消除了脉冲干扰,保留了信号的冲击特征。滤波后的6个分量信号的峭度值如表2所示,选取峭度最大分量(分量信号6,峭度值为20.694 9)和次大分量(分量信号5,峭度值为13.008 6)进行信号重构,重构信号如图4(c)所示,可以看出,冲击成份特别明显,适合用于作为故障特征信号的提取。通过TKEO计算重构后的瞬时能量进而对其进行频谱分析,其能量谱如图5所示,图中清晰定位到了外圈故障的基频105.5 Hz(与理论故障频率103.36 Hz接近),倍频可有效定位到9倍频,因此,可准确判断轴承处于外圈故障状态。将本文的方法与文献[3]中采用的方法进行对比,文献[3]外圈特征提取结果如图6所示。可以看出虽然能提取到基频,但高频的故障特征频率不明显,高频部分难免夹杂着部分噪声信息,倍频信息易被噪声所掩盖,效果较图5差。 表2 外圈故障分量信号的峭度指标 图4 外圈故障信号的SVD分析结果 图5 本文方法TKEO能量谱 图6 文献[3]外圈特征提取结果 针对强噪声干扰背景下微弱故障特征信息难以提取的问题,提出了基于SVD—形态降噪的TKEO故障诊断方法。通过奇异值贡献率选择Hankel矩阵的维数,对确定维数的Hankel矩阵进行奇异值分解;对得到的分量信号通过形态学滤波器进行滤波,并利用峭度准则,筛选出峭度故障特征明显的SVD分量,用于信号重构。TKEO计算突变信息的瞬时能量,得到故障信号的能量谱,从而提取振动信号的特征。轴承诊断实例的结果表明,该方法能够获得清晰的轴承故障特征,提高了故障诊断的准确性。 [1] 马文龙,吕建新,吴虎胜,等.多传感器信息融合在滚动轴承故障诊断中的应用[J].传感器与微系统,2013,32(7):132-135. [2] 张金敏,翟玉千,王思明.小波分解和最小二乘支持向量机的风机齿轮箱故障诊断[J].传感器与微系统,2011,31(1):41-43. [3] 赵学智,叶邦彦,陈统坚.奇异值差分谱理论及其在车床主轴箱故障诊断中的应用[J].机械工程学报,2010,46(1):100-108. [4] 杨本娟,黎小平.基于核主成分分析的图像模糊篡改检测算法[J].传感器与微系统,2015,34(11):137-139. [5] 王奉涛,陈守海,闫达文,等.基于流形—奇异值熵的滚动轴承故障特征提取[J].振动.测试与诊断,2016(2):288-294. [6] Raj S,Murali N.Early classification of bearing faults using morphological operators and fuzzy inference[J].IEEE Transactions on Industrial Electronics, 2013,60(2):567-574. [7] 汤宝平,将永华,张详春.基于形态奇异值和经验模态分解的滚动轴承故障特征提取方法[J].机械工程学报,2010,46(5):37-48. [8] Jiang Huiming,Chen Jin,Dong Guangming,et al.Study on Hankel matrix-based SVD and its application in rolling element bearing fault diagnosis[J].Mechanical Systems and Signal Processing,2015,53:338-359. [9] 赵学智,叶邦彦,陈统坚.矩阵构造对奇异值分解信号处理效果的影响[J].华南理工大学学报:自然科学版,2008,36(9):86-93. [10] 赵 昭,刘利林,张承学,等.形态学滤波器结构元素选取原则研究与分析[J].电力系统保护与控制,2009,37(14):21-25. [11] 杜 钊,李宏伟,张建忠.L-DACS中的信号分离算法的研究[J].传感器与微系统,2012,31(6):45-48. [12] 吴小涛,杨 锰,袁晓辉,等.基于峭度准则EEMD及改进形态滤波方法的轴承故障诊断[J].振动与冲击,2015,34(2):38-44. [13] 武 哲,杨绍谱,张建超.基于LMD自适应多尺度形态学和Teager能量算子方法在轴承故障诊断中的应用[J].振动与冲击,2016(3):7-13. [14] Case Western Reserve University,Bearing Data Center.Bearing data center fault test data.[EB/OL].[2009—10—01].http:∥www.eecs.case.edu/laboratory/bearing. Research on TKEO fault diagnosis method based on SVD-morphological noise reduction* HUANG Gang-jin1,2, FAN Yu-gang1,2, FENG Zao1,2, QI Peng1,2 (1.Faculty of Information Engineering & Automation,Kunming University of Science and Technology,Kunming 650500,China;2.Engineering Research Center for Mineral Pipeline Transportation,Yunnan Province,Kunming 650500,China) Aiming at problem of extracting weak characteristics from the fault signals containing strong background noise,a method based on singular value decomposition(SVD)-morphological noise reduction for Teager-Kaiser energy operator(TKEO) fault diagnosis is proposed.Firstly,bearing vibration signal is decomposed by SVD,the component signals are filtered by morphological filter to remove the noise; Secondly,the component signals are screened and reconstructed using kurtosis criterion;Finally,the instantaneous energy of reconstructed signals are calculated by using the TKEO,the energy spectrum of the signals are then obtained,from which the characteristics of the vibration signals are extracted.The experimental results show that the proposed method is capable of extracting fault features and has offered an approving performance on fault diagnosis of rolling bearing. singular value decomposition(SVD); morphological filtering; Kurtosis criterion; Teager-Kaiser energy operator(TKEO);fault diagnosis 10.13873/J.1000—9787(2017)07—0029—04 2016—08—02 国家自然科学基金资助项目(61563024,51169007);云南省中青年学术和技术带头人后备人才培养计划项目(2011CI017) TH 165.3 A 1000—9787(2017)07—0029—04 黄刚劲(1992-),男,硕士研究生,主要研究方向为信号处理、模式识别、机械故障诊断。2 Teager能量谱的构建

3 基于组合SVD —形态降噪的TKEO故障诊断方法
4 滚动轴承故障诊断实验
5 结 论
