爆轰流体力学模型敏感度分析与模型确认∗
2017-08-09梁霄1王瑞利1
梁霄1)2) 王瑞利1)†
1)(北京应用物理与计算数学研究所,北京 100094)
2)(山东科技大学数学学院,青岛 266590)
爆轰流体力学模型敏感度分析与模型确认∗
梁霄1)2) 王瑞利1)†
1)(北京应用物理与计算数学研究所,北京 100094)
2)(山东科技大学数学学院,青岛 266590)
(2017年1月14日收到;2017年3月13日收到修改稿)
验证、确认与不确定度量化(V&V&UQ)是评估物理模型可信度和量化复杂工程数值模拟结果置信度的系统方法.验证是要回答数值模拟程序是否正确求解了物理模型和程序是否正确实施或给出求解模型的误差、不确定性大小及使用范围,确认是要通过数值结果回答物理模型是否反映了真实客观世界或反映真实客观世界的可信程度.文章围绕爆轰流体力学模型,剖析了模型中不确定性因素,给出了影响模拟结果不确定性的关键因素清单,并对其开展了敏感度分析,确认了模型的适应性.
爆轰流体力学模型,不确定度量化,敏感度分析,模型确认
1 引言
爆轰是极为复杂物理化学过程,同时在极小时间和空间尺度发生,且炸药具有复杂的物质构成,是爆炸力学研究的重点也是难点.实验、理论、数值模拟是现代爆轰研究的三种支柱.三种方法相互依存,并各有千秋.目前的症结在于:化学反应过程的精密化实验研究能力不足,物理建模本身先进性不足.并且爆轰实验成本过于昂贵,仅能提供有限的数据;或炸药感度过高,使得研究人员处于一种危险的操作环境;或理论无法解释的复杂多物理过程,数值模拟成为研究爆轰的一种快捷经济的途径.
人们希望逼真建模与精确仿真,研制高可信度的爆轰数值模拟软件,再现爆轰发生的过程.但在爆轰数值模拟过程中,由于炸药爆轰过程的复杂性和人们认知的局限性,在物理建模过程中不仅含有抽象、简化和近似,而且在数值模拟过程中有很多不确定性因素.爆轰流体力学过程采用的物理模型含有数十个不确定性参数和难以用统一形式描述的唯象反应率、产物状态方程等多种唯象模型,严重影响数值模拟结果的置信度,使得决策承担很大风险,主要原因是模型不确定性未得到有效量化,数值模拟结果的可信度难以把握,此问题一直未得到很好的解决[1−4].模型验证与确认(veri fi cation and validation,V&V)源自于美国,于1979年由美国计算机模拟协会正式提出.主要通过科学方法、标准流程、专业算法、精密层级试验,不断为数值模拟程序的正确性和物理模型的适应性进行证明,并据此建立模型的可信度[5−7].不确定度量化(uncertainty quanti fi cation,UQ)是将物理实验和数值模拟有效结合,是V&V的核心,其充分利用实验的价值,不断认识物理模型的不确定度,逐渐缩小物理模型再现过程与实际演化过程的差距[8−12],完善物理模型,发展高可信度数值模拟软件,最终达到基于科学模拟这条最佳途径和有限实验,为复杂系统可靠性认证、性能评估和事故分析提供有效证据.2001年,隶属于美国的Sandia实验室、Los Alamos实验室、Lawrence Livermore实验室将UQ用于核武器库存安全管理,并给出了认知不确定度和偶然不确定度量化在核反应堆故障排除和放射性核废料处理中的应用[13].敏感度分析是指从众多不确定性因素中找出对现象、事件、过程中某特量指标有重要影响的敏感性因素,分析其对特量指标的影响程度,进而判断现象、事件、过程的承受风险能力的一种不确定性分析方法.本文主要是针对计算模型、计算参数、数值方法等输入不确定性,对输出模拟结果的影响程度,以确认物理模型的参数或形式.
美国国家核安全局对火星探测器再入系统通过6000次数值计算和敏感性分析,将系统初始417个独立变量消减至不足10个核心参数,并对每个核心参数进行了UQ,为系统性能优化和全系统试验节省了大量成本.目前,国际上爆炸领域的敏感度研究侧重于炸药起爆的难易,强调炸药物性的敏感程度[14],简称“感度”,对于爆轰数值模拟输入参数不确定性对输出响应量影响程度的敏感度分析尚未见报道.Romick等[15]给出了黏性氢-空气爆轰的验证与确认,Bdzil和Stewart[16]给出了包覆惰性材料的凝聚炸药的模型确认.当爆轰系统不确定性参数较多时,本文探讨了含有大量不确定性输入参数的爆轰模型的有效性和可靠性的确认问题.
2 爆轰流体力学模型与不确定度
2.1 爆轰流体力学方程组
炸药爆轰过程所使用的模型为守恒原理的双曲型偏微分方程组,表征炸药化学反应的常微分方程以及复杂非线性函数关系式耦合方程组如下:
质量方程

动量方程

能量方程

状态方程

炸药反应率
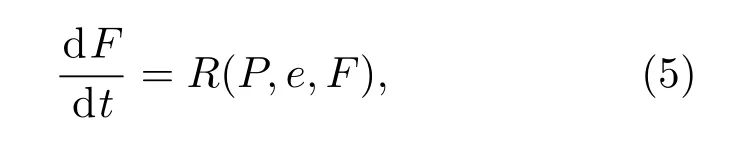
其中:ρ,u,E,e,P分别表示密度、速度、总能、内能与压力;uu为并矢张量;u·u是内积;为爆轰产物的燃烧函数.(5)式求解上没什么困难,主要问题是提供一个能正确反映炸药化学反应特性的函数关系式R(P,e,F).
2.2 炸药反应率唯象模型
爆轰是极为复杂物理化学过程,同时在极小的时间和空间尺度发生.因此从理论上严格建立反应率方程是很困难的,目前只能采用唯象近似.常用模型如Arrhenius反应率模型、Cochran反应率模型、Lee反应率模型、Forest Fire反应率模型、Wilkins反应率模型等.
本文采用Wilkins反应率模型研究爆轰.F=0为凝固炸药(未反应)区;0 其中:F1为CJ比容燃烧函数,F2为时间燃烧函数,nb是可调参数. 其中v=1/ρ表示比容,v0是初始比容,vJ=γv0/(γ+1)是CJ比容,γ是多方指数(理想气体常数),tb是起爆时间[10];∆L=rb∆R/DJ,∆R表示网格宽度,DJ是爆速,rb可调. 由于反应率模型是唯象的,并没有坚实的物理基础,我们需要大量的实验评估模型的应用范围和局限. 2.3 物态方程(EOS)唯象模型 爆炸产物常采用Jones-Wikins-Lee(JWL)形式的物态方程,其形式为[17−21] 其中PJ,VJ是炸药CJ状态下的爆压、比容,VJ=是爆热. 2.4 爆轰流体力学建模与模拟中的不确定性 不确定性是研究物理模型在有准确输入或不准确输入条件下的模拟问题,以及由建模与模拟本身的随机性、模型认知缺陷以及近似求解导致的不确定性问题.爆轰流体力学多物理耦合建模与模拟中的不确定性分类见文献[3].这些不确定性问题直接影响了建模与模拟的置信度.即使采用上述确定性数学模型及求解方法求解时,其ρ,u,E,e,p不仅是时间t和空间位置(x,y,z)的函数,还是随机变量ξ的函数.计算区域网格划分尺度∆R和计算时间步长∆t以计算收敛稳定为准,初始物理量如初始密度ρ0也可当成随机变量,表1简单罗列了爆轰流体力学建模与模拟下输入参数不确定性的因素. 表1 爆轰流体力学中的不确定性因素Table 1.Sources of uncertainty in detonation CFD coupled with multi-physics. 在复杂工程建模与模拟的确认活动中,通过确认技术及不确定度量化方法可以给出数值模拟的不确定度Usimulation,但物理模型(单一过程、基准模型)或模拟过程(子系统模拟、全系统模拟)是否刻画客观实际,最终还必须依靠确认试验.确认试验是模型形式、参数和取值范围以及多物理耦合过程中多模型匹配确认的核心(如图1). 3.1 模型形式中关键参数清单 针对复杂工程单一模型,其中有可能存在几个参数或几十个参数,有的对结果的影响不敏感,有相关.利用爆轰波阵面上的守恒关系以及CJ爆轰条件,推出的对结果影响很大,甚至影响不可接受.在确认的过程中,首先必须对参数做敏感度分析,给参数的影响建立清单,梳理出关键的影响参数. 假设某模型涉及参数为:p1,p2,···,pn,经代入确定性程序计算,针对某些响应量数值模拟结果进行敏感度分析,敏感度为sp1,sp2,···,spn.由此选出关键影响参数为b1,b2,···,bn. 同样针对此模型实施单一试验或基准试验,针对响应量测量数据,开展敏感度分析,敏感度为sp1,sp2,···,spn.由此选出关键影响参数为a1,a2,···,an. 图1 (a)模型适应性确认方法及流程;(b)敏感度分析及关键因素不确定度量化流程Fig.1.(a)Validation methods and procedure for model adaptation;(b)sensitivity analysis and uncertainty quanti fi cation procedure for key factor. 3.2 模型形式中关键参数值及影响范围确认 模型形式中关键参数值及影响范围确认涉及两个方面. 1)试验不确定度量化.根据试验关键影响参数a1,a2,···,an,假设实验测试数据为˜σexperiment,它的不确定度为˜uuncertainty.假设由试验不确定度量化方法得到每个参数的不确定度为∆a1,∆a2,···,∆an,则 对于试验的不确定度,有时分为三种类型: a)试验是确定的,即˜uuncertainty=0; b)由于信息不完备,˜uuncertainty̸=0,需要发展量化方法; c)即(13)式能确定的不确定度. 2)数值模拟不确定度量化.根据数值模拟关键影响参数b1,b2,···,bn,假设数值模拟结果为σvalue,它的不确定度为uuncertainty.假设由数值模拟不确定度量化方法得到每个参数的不确定度为∆b1,∆b2,···,∆bn,则 数值模拟结果的不确定度uuncertainty包括两个方面:物理模型的不确定度umodel和数值计算的不确定度ucomputation.这样(14)式可表示为 数值计算可能涉及几个或多个因素,不妨假设为c1,c2,..,cn,由数值模拟可得到每个因素影响的不确定度∆c1,∆c2,···,∆cn,即可得到 由(14)—(16)式就可以得到模型参数的不确定度. 但由于数值计算有些因素的不确定度很难量化,如计算机舍入误差,有时可以忽略,有时不能忽略,这样对(17)式要考虑一个修正项∆ucomputation,即得 由(13)式与(18)式就可以确认模型关键参数的值与范围.这里分为如下几种情况: a)如果˜uuncertainty≈umodel,就直接确定了模型参数值和范围; b)如果umodel∈˜uuncertainty,工程设计认为在多大范围内能接受,也就确定了模型参数值和范围; c)如果˜uuncertainty∈umodel一般是可接受的,但要确认模型参数值和范围,需要改进试验; d)如果˜uuncertainty∩umodel̸=0,且不存在包含关系,则由它们之间夹的面积衡量是否可接受.如果不能接受,需要调整参数; e)如果˜uuncertainty∩umodel=0,˜uuncertainty/∈umodel,必须通过调整参数值和范围,达到等价或包含关系,然后确定模型参数值和范围. 3.3 模型最佳形式的确认 通过对单个模型参数和范围的确定,然后不同模型形式之间进行对比,就可以确定那种模型形式好,以选取最佳模型形式. 3.4 多过程(多模型)确认 从上面可以看出,在复杂工程理论研究中,模型参数与形式的确认,单一试验很重要.实际上复杂系统除了单一模型和基准模型外,还有子系统级和系统级模型的确认,即多物理过程耦合(多模型组合)的确认,类似于单一模型,需要子系统级和系统级的确认试验,确定了多物理过程模型.这也就是在建模与模拟确认阶段确认层级中四个层级的确认过程. 4.1 敏感度分析的爆轰计算模型 从第3节可以看出,敏感度分析在爆轰模型确认中非常重要.为了确定爆轰模型的输入参数,一般进行“圆筒试验”.对于不同的炸药,要确定其JWL参数,不论是圆筒试验还是进行数值模拟,都会花费大量的人力、财力、物力,对于昂贵或新研制的炸药则更加困难,因此,需要一种更为方便快捷的方法来确定JWL的待定参数. 圆筒试验几何形状和尺寸如图2所示.炸药为TNT,性能参数:γ=3.1,ρ0=1.634 g/cm3,DJ=6.932 km/s.紫铜物性参数:γ=3.68,ρ0=8.93 g/cm3,c0=3.94 km/s.在O点起爆或者面爆.计算采用拉氏自适应流体动力学软件LAD2D[12]. 图2 圆筒试验模型结构Fig.2.Model structure of cylinder test. 4.2 参数敏感度分析及关键参数量化 表2给出了各因素敏感性分析结果.计算参数除了因素栏说明外,其余均按统一计算条件取值.其中JWL参数取R1=4.6,R2=1.3,ω=0.38;燃烧函数中参数取nb=1.3,rb=2.1;采用压缩比起爆时取σ=1.03,采用时间起爆时,按惠更斯原理计算起爆时间. 表2 各因素敏感性分析结果Table 2.Sensitivity analysis results of di ff erent factor. 从表2,根据响应量爆压、爆速及管壁位置的影响范围,可以看出12个因素影响大小排序为:1)体积起爆燃烧函数nb;2)体积起爆燃烧函数rb;3)体积起爆σ阈值;4)起爆方式;5)时间起爆燃烧函数nb;6)时间起爆燃烧函数rb;7)时间起爆JWL-EOS中R1;8)时间起爆JWL-EOS中R2;9)体积起爆JWL-EOS中R1;10)体积起爆JWLEOS中R2;11)体积起爆JWL-EOS中ω;12)时间起爆JWL-EOS中ω.根据敏感度分析,可认为爆轰模型的关键参数是基于体积起爆下燃烧函数中参数nb和参数rb.由经验取nb∈[0.85,2.20],rb∈[1.65,3.00],利用PC方法,对关键参数进行了不确定度量化.图3给出了nb∈[0.85,2.20],rb∈[1.65,3.00]均匀抽样4次PC给出空间压力的期望值及方差.图4给出了爆轰模型计算出的爆压、爆速随时间变化的期望值及方差.图5给出了圆筒管壁位置随时间变化的期望值及方差. 图3 (网刊彩色)不同时刻压力空间分布的期望值与方差Fig.3.(color online)Spatial distribution of expectation and variance of pressure at di ff erent times. 图4 (网刊彩色)爆轰模型模拟爆压、爆速与解析解比较Fig.4.(color online)Comparison between analytical solution and simulation result for detonation pressure,detonation velocity from detonation model. 图5 (网刊彩色)圆筒管壁按时间的期望值与方差(其中点为试验数据)Fig.5.(color online)Expectation and variance of position of cylindrical wall versus time(dotted line represents the experiment data). 4.3拐角绕爆 拐角效应的数值模拟对研究炸药性能和合理设计弹体等有着十分重要的意义,为了有效模拟拐角绕爆问题,对此问题开展了模型确认.图6是此问题的模型结构,炸药取PBX-9404炸药,性能参数为ρ0=1.842g/cm3,DJ=8.88 km/s.炸药采用JWL状态方程和Wilkins反应率模型.为了开展此问题计算敏感度的分析,我们在计算模型中选取了A和B两个(距离拐角分别是0.466667 cm,0.033333 cm)拉氏参考点. 图6 绕爆模型结构及计算条件(A和B为拉氏参考点)Fig.6.Computational structure and conditions for detonation wave behind a backward-facing step(Lagrangian reference point A and point B). 图7 (网刊彩色)拉氏参考点A位置和速度随时间的变化Fig.7.(color online)The position and velocity for Lagrangian reference point A versus time. 图8 (网刊彩色)拉氏参考点B位置和速度随时间的变化Fig.8.(color online)The position and velocity for Lagrangian reference point B versus time. 在拐角效应的数值模拟中,网格尺度与JWL状态方程系数对其计算结果影响比较大.为此我们对此两个因素开展了敏感度分析.计算网格规模选取6750单元,27000单元,108000单元的三种网格规模,JWL状态方程系数R1,R2选取(R1=5.95,R2=1.845),(R1=4.9,R2=1.39),(R1=4.9,R2=2.3),(R1=7.0,R2=2.3)的四组参数,w=0.38,A和B由(10)—(12)式关系式确定,Wilkins反应率中参数分别为nb=1.1,γb=2.1.图7和图8分别给出了计算网格和JWL参数对拉氏参考点A和B位置和速度随时间变化的敏感程度. 从图7和图8可以看出,当计算网格规模为6750时,JWL状态方程参数不确定性对计算结果的分散度比较大(蓝线),当计算网格规模为27000时,JWL状态方程参数不确定性对计算结果的分散度很小(绿线),在继续增加计算网格规模到108000时,JWL状态方程参数不确定性对计算结果的分散度(粉线)与计算网格规模为27000时基本一致,达到稳定.这样,通过敏感度分析,确定了拐角效应的数值模拟时爆轰的计算模型. 1)基于圆筒试验通过敏感度分析,对爆轰计算模型进行了确认,可以看出TNT的压力期望为16 GPa,标准差为2.2 GPa,位置与爆速基本与实验一致.说明采用的JWL状态方程和Wilkins反应率模型计算的爆轰模型基本适应. 2)将其敏感度分析方法应用于拐角效应的模拟,确认了JWL状态方程参数与计算网格规模.JWL状态方程参数不确定性对计算结果的影响与计算网格尺度关系很大,当计算网格尺度到一定程度时,JWL状态方程参数的不确定性对计算结果的影响逐渐缩小,逐渐趋于稳定. 本文给出了应用程序M&S的V&V的含义,明确了验证与确认的基本内容,着重描述了复杂工程M&S适应性确认方法,包括物理模型、实(试)验、参数梳理、数值模拟与参数不确定度量化,以及模拟结果与实验一致性,给出了模型适应性.后续的工作需要注意以下问题: 1)爆轰模型形式及参数梳理是保证爆轰流体力学建模与模拟适应性确认的重要前提,对于复杂工程应用程序,必须开展敏感度分析,给出响应量影响大小排序是确认模型的关键; 2)对参数首先必须开展不确定性量化,其次是需要结合相关实验/试验数据,判断模型形式及参数值或范围; 3)围绕爆轰流体力学模型,剖析了模型中的不确定性因素,给出了影响模拟结果不确定性的关键因素清单,并对其开展了敏感度分析,确认了模型的适应性. [1]Zhang G R,Chen D N 1991 Detonation Dynamics of Agglomerate Detonator(Beijing:National Defense Industry Press)(in Chinese)[张冠人,陈大年1991凝聚炸药起爆动力学(北京:国防工业出版社)] [2]Sun J S 1995 Adv.Mech.25 127(in Chinese)[孙锦山1995力学进展25 127] [3]Wang R L,Jiang S 2015 Sci.Sin.:Math.45 723(in Chinese)[王瑞利,江松2015中国科学数学45 723] [4]Wang C,Shu C W 2015 Chin.Sci.Bull.60 882(in Chinese)[王成,Shu Chi-Wang 2015科学通报60 882] [5]Oberkampf W L,Roy C L 2010 Veri fi cation and Validation in Scienti fi c Computing(New York:Cambridge University Press)p229 [6]Liang X,Wang R L 2016 Expl.Shock Waves 36 509(in Chinese)[梁霄,王瑞利2016爆炸与冲击36 509] [7]Wang R L,Liang X,Lin W Z,Liu X Z,Yu Y L 2016 Defect&Di ff usion Forum 366 40 [8]Wang R L,Zhang S D,Liu Q 2014 AIP Conf.Proc.1648 [9]Wang R L,Liu Q,Wen W Z 2015 Expl.Shock Waves 35 9(in Chinese)[王瑞利,刘全,温万治2015爆炸与冲击35 9] [10]Tang T,Zhou T 2015 Sci.Sin.:Math.45 891(in Chinese)[汤涛,周涛2015中国科学数学45 891] [11]Wang R L,Lin Z,Wei L,Liu X Z 2015 Chin.J.High Pressure Phys.29 286(in Chinese)[王瑞利,林忠,魏兰,刘学哲2015高压物理学报29 286] [12]Wang R L,Lin Z,Wen W Z 2014 Comput.Aided Engin.23 1(in Chinese)[王瑞利,林忠,温万治2014计算机辅助工程23 1] [13]Liang X,Wang R L 2016 Chin.J.High Pressure Phys.30 223(in Chinese)[梁霄,王瑞利2016高压物理学报30 223] [14]Ng H,Ju Y,Lee J 2007 Int.J.Hydrogen Energy 32 93 [15]Romick C,Aslam T,Powers J 2015 J.Fluid Mech.769 154 [16]Bdzil J,Stewart D 2007 Anna.Rev.Fluid Mech.39 263 [17]Wang Y J,Zhang S D,Li H,Zhou H B 2016 Acta Phys.Sin.65 106401(in Chinese)[王言金,张树道,李华,周海兵2016物理学报65 106401] [18]Zhou H Q,Yu M,Sun H Q,Dong H F,Zhang F G 2014 Acta Phys.Sin.63 224702(in Chinese)[周洪强,于明,孙海权,董贺飞,张凤国2014物理学报63 224702] [19]Song H,Tian M,Liu H,Song H,Zhang G 2014 Chin.Phys.Lett.31 016402 [20]Zhou Z,Nie J,Guo X,Wang Q 2015 Chin.Phys.Lett.32 016401 [21]Chang Z,Meng X,Lu X 2016 Physica A 472 103 PACS:64.30.–t,82.20.Wt,87.16.A–DOI:10.7498/aps.66.116401 Sensitivity analysis and validation of detonation computational fl uid dynamics model∗ Liang Xiao1)2)Wang Rui-Li1)† 14 January 2017;revised manuscript 13 March 2017) Veri fi cation,validation and uncertainty quanti fi cation(V&V&UQ)is a method of assessing the credibility of physical model and quantifying the con fi dence level of numerical simulation result in complex engineering.Veri fi cation is used to answer the question whether the physical model is well solved or the program is implemented correctly,and it will give the ranges of error and uncertainty.Validation is used to answer the question whether the physical model re fl ects the real world or the con fi dence level of the physical model.This article deals with the detonation computational fl uid dynamics model,and analyses the uncertainty factor in modeling,then presents the key factor which a ff ects the accuracy of the simulation result.Due to the complexity of the explosive detonation phenomenon,there are a huge number of uncertainty factors in the detonation modeling.The sensitivity analyses of these uncertainty factors are utilized to distinguish the main factors which in fl uence the output of the system.Then uncertainty quanti fi cation is conducted in these uncertain factors.After comparing the simulation result with the experiment data,the adaptation of the model is validated.This procedure is applied to the cylindrical test with TNT explosive.From the result,we can see that the parameters in the JWL EOS are calibrated and the accuracy of the model is validated.By the way,through conducting the uncertainty quanti fi cation of this system,we obtain that the expectation and standard deviation of detonation pressure for TNT are 1.6 and 2.2 GPa respectively.Detonation velocity and position of the cylindrical wall accord well with the experiment data.That means that the model is suited in this case.This technique is also extended to the detonation di ff raction phenomenon.We can conclude that simulation result is greatly a ff ected by the scale of the cell.From these examples,we can infer that this method also has a wide application scope. detonation computational fl uid dynamics model,uncertainty quanti fi cation,sensitivity analysis,model validation 10.7498/aps.66.116401 ∗国家自然科学基金(批准号:11372051,91630312,11475029)、中国工程物理研究院科学基金(批准号:2015B0202045)、山东省自然科学基金(批准号:ZR2015AQ001)和国防科工局国防基础科研计划(批准号:C1520110002)资助的课题. †通信作者.E-mail:wang_ruili@iapcm.ac.cn ©2017中国物理学会Chinese Physical Society http://wulixb.iphy.ac.cn *Project supported by the National Natural Science Foundation of China(Grant Nos.11372051,91630312,11475029),the Fund of the China Academy of Engineering Physics(Grant No.2015B0202045),the Natural Science Foundation of Shandong,China(Grant No.ZR2015AQ001),and the Defense Industrial Technology Development Program,China(Grant No.C1520110002). †Corresponding author.E-mail:wang_ruili@iapcm.ac.cn


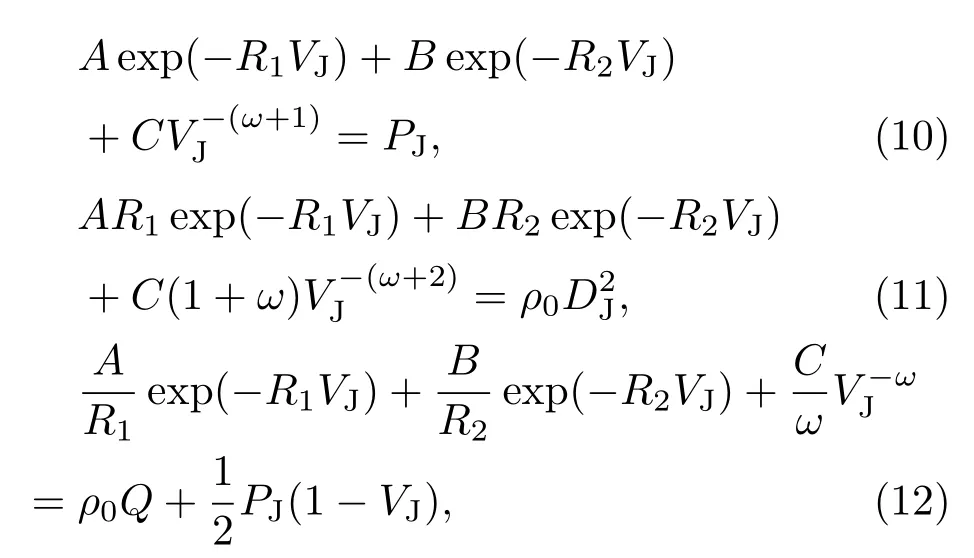

3 爆轰流体力学模型适应性确认方法


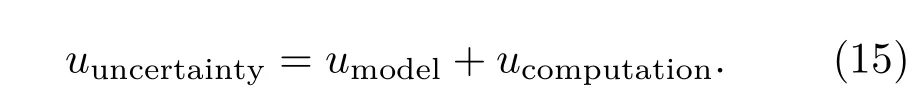


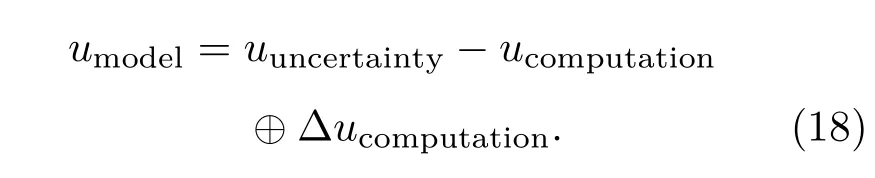
4 爆轰流体力学模型中参数敏感度分析
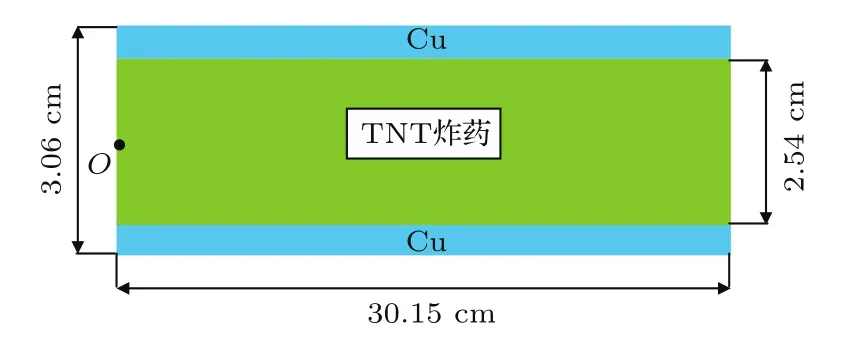
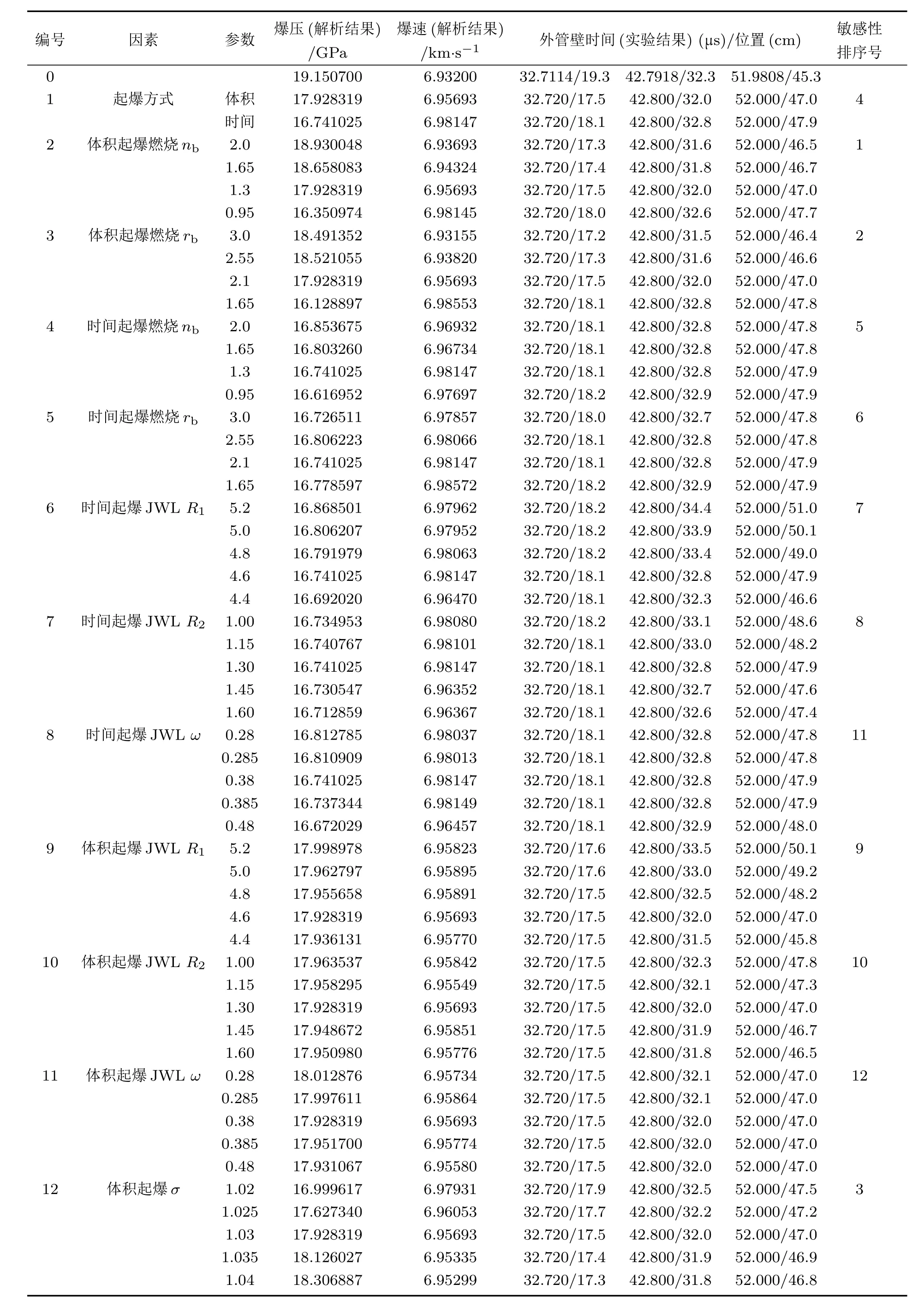
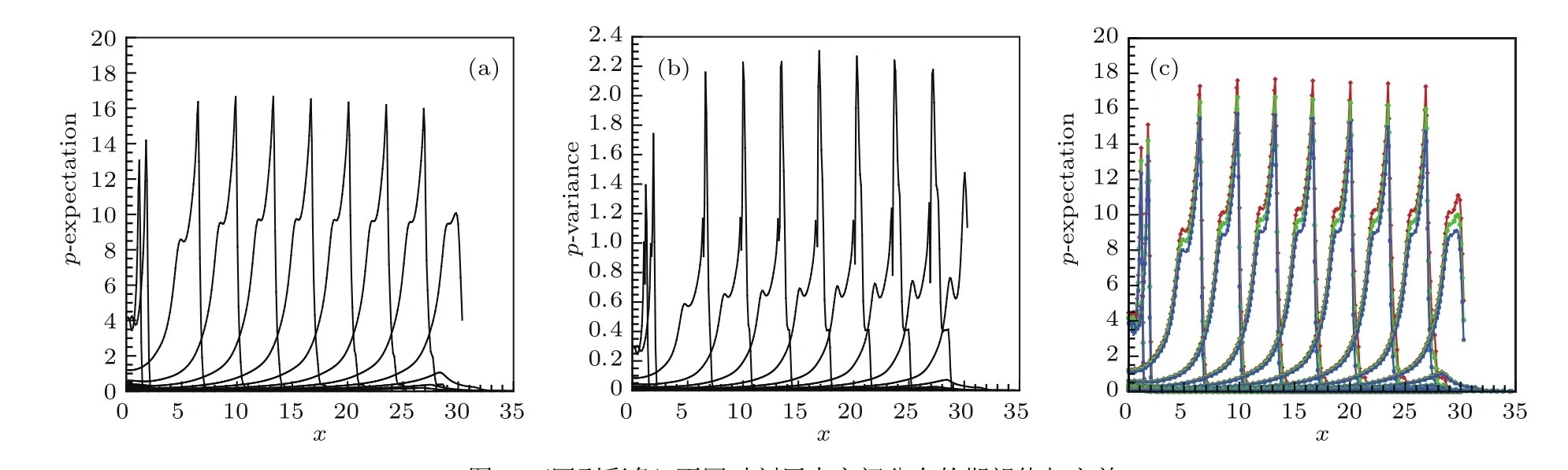


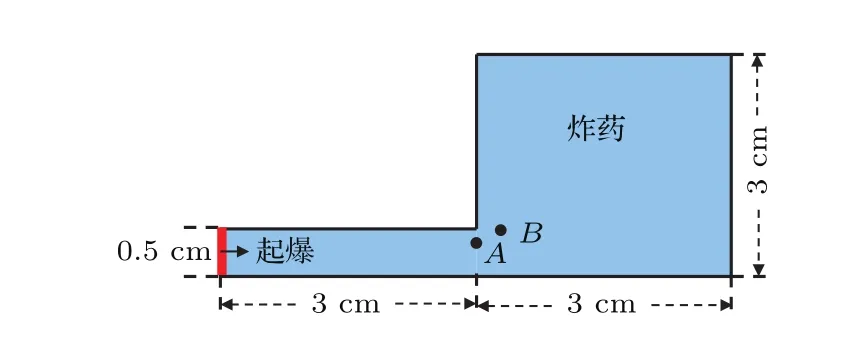
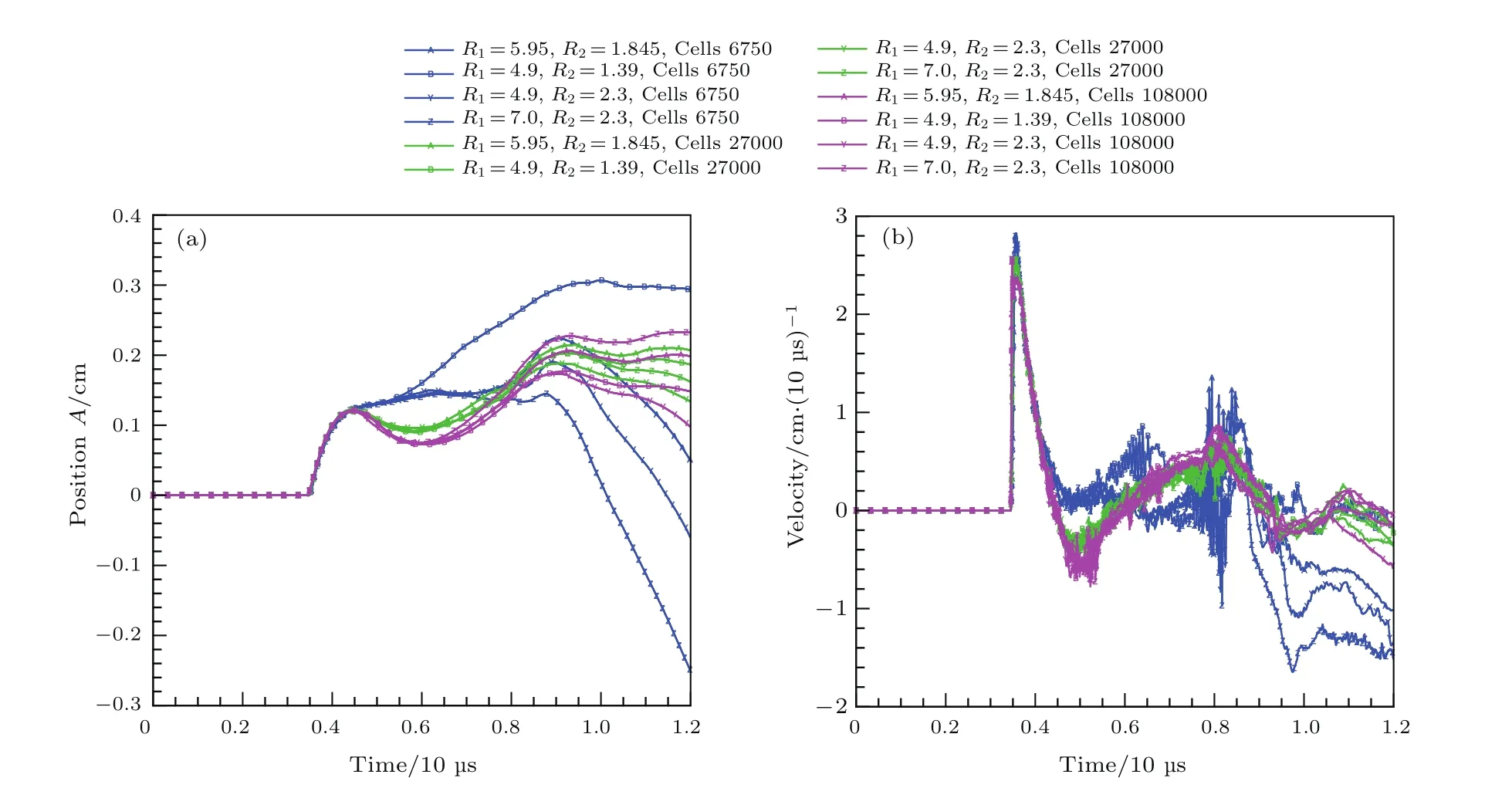
5 结论
1)(Institute of Applied Physics and Computational Mathematics,Beijing 100094,China)
2)(College of Mathematics,Shandong University of Science and Technology,Qingdao 266590,China)
