基于光纤光栅的振动检测系统设计
2017-08-09作者魏晨吉林大学珠海学院
作者/魏晨,吉林大学珠海学院
基于光纤光栅的振动检测系统设计
作者/魏晨,吉林大学珠海学院
本文以光纤布拉格光栅为传感器件,采用长周期光纤光栅线性边缘滤波动态解调法,以LabVIEW为软件开发平台,实现了等强度悬臂梁的低频率微小振动测量。实验表明,在振动频率小于1kHz,振幅在12~28mm范围内,测量具有较好的准确度和重复性。
振动;光纤光栅;动态解调;LabVIEW
引言
光纤光栅传感器具有抗电磁干扰能力强、灵敏度高、体积小、质量轻、易于实现分布式传感的优点,广泛应用于应变、温度、压力、振动等物理量的测量。光纤光栅是波长调制型传感器,中心波长解调是关键技术,常见的解调方法有光谱分析法、可调谐光源检测法、非平衡迈克尔逊干涉仪解调法[1]等。本文采用长周期光纤光栅线性边缘滤波解调法,实现振幅和频率参数的测量。
1. 光纤光栅的传感特性
光纤光栅是纤芯折射率周期性变化的光纤器件。当宽带光源入射到光纤布拉格光栅(FBG)上时,会反射回一个窄带光波,其中心波长称为布拉格波长,记为λB,满足下式[2]:

其中nef为纤芯模的有效折射率,Λ为光栅周期。应变和温度是引起nef和Λ变化的最直接的因素,进而使布拉格波长产生偏移,通过测量偏移量可以间接测得外界物理量。基于光纤光栅传感器的传感过程是通过外界参量对光纤光栅中心波长的调制来获得传感信息,实质上是一种波长调制型光纤传感器。
2. 长周期光纤光栅的线性边缘滤波解调法
长周期光纤光栅(LPG)透射光的中心波长记为λL,满足下式:

其中,nc0和nc1(m)分别为纤芯模和m阶包层模的有效折射率,Λ为光栅周期。
LPG的透射特性类似于带阻滤波器,中心波长两边的曲线线性度较好,可作为滤波区间。解调时要保证FBG的中心波长落在长周期光纤光栅的线性区域中。图1为长周期光纤光栅解调示意图。振动使悬臂梁偏移原来的平衡位置,粘在悬臂梁上的FBG受到应力,发生形变。当形变增大时,布拉格波长向长波方向移动,由原来的位置a移到位置b,经过LPG滤波后,光强变强;当形变减小时,布拉格波长向短波方向移动,LPG输出端光强变弱。通过光强的变化可以得知布拉格波长的变化,从而间接得知振幅。

图1 长周期光纤光栅解调示意图
3. 系统设计
系统硬件由光纤布拉格光栅传感、长周期光纤光栅解调、光电转换、信号调理电路、数据采集卡和计算机组成,结构如图2所示。光纤布拉格光栅粘贴在等腰悬臂梁上,用以感知悬臂梁的振动。光电探测选用InGaAsPIN光纤耦合输出探测器,将长周期光纤光栅透射的光信号转换为电信号,该电信号为电流信号。信号调理电路包括I/V转换电路和放大电路。数据采集卡选用NI公司的USB6009,具有14Bit分辨率和48KS/s的采样率,实现模拟量到数字量的转换,并传送到计算机中。
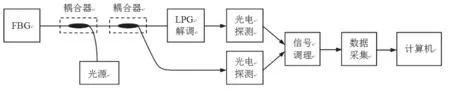
图2 振动测试系统硬件结构框图
软件部分以LabVIEW为开发平台,主要完成滤波和数据处理。考虑到测量装置在静态标定、校准时应使用低通滤波器,动态测量时应使用带通滤波器,若用模拟滤波器实现较为复杂,因此选用LabVIEW中的软件滤波器,更换滤波器类型、参数十分方便。先对采集到的数据进行进制转换;再经巴特波斯滤波器滤波,消除噪声;每40个数据取均值消除不稳定因素的影响,数据个数的选择可根据采样频率进行设定;最后将测试结果的图像和数值显示在前面板。
4. 实验设计
4.1 线性标定
线性标定采用螺旋测微仪改变悬臂梁末端位移量,模拟振动振幅,如图3所示。等腰悬臂梁在同一轴线上所受应力强度相等。根据材料力学原理,悬臂梁表面沿中心轴方向的应变ε与末端位移x在一定范围内呈线性关系[3]。已知波拉格波长λB与轴向应变ε成正比关系,故波拉格波长与螺旋测微仪的进给量成正比关系。将FBG的一个接头与光源连接,另一个与光谱仪连接,调节螺旋测微仪,悬臂梁受到应力,带动粘在悬臂梁上的光纤布拉格光栅产生应变,记录下螺旋测微仪在不同位置时由光谱仪测得的布拉格波长。拟合直线方程为λB=0.109x+1546.8,灵敏度为109pm/mm,相关指数R2=0.9993,直线与原数据点拟合度好。其中波长单位为纳米,位移单位为毫米。
按照线性边缘滤波法原理图连接光路,光源经耦合器进入光纤布拉格光栅,经光纤布拉格光栅反射后的光通过耦合器分成两路,一路与长周期光纤光栅相连,长周期光纤光栅的另一端与光功率计相连。调节螺旋测微仪到前一过程记录的位置,分别记录下光功率计的示数P。光功率和波拉格波长λB的拟合直线为P=7.37λB—11373.05,光功率随波长的变化率为7.37nW/nm,相关指数R2=0.9989,拟合度好。其中光功率单位为毫瓦。
光功率与电路输出电压成正比,参考光路的光功率始终保持不变,对应输出电压也保持不变。数据采集卡对两路电压信号进行采集,经过LabVIEW数据处理,传感电压值与参考电压值之比称为θ。调节螺旋测微仪到前一过程记录的位置,分别记录下比值θ。拟合直线方程为λB=10.17θ+1544.9,二者成正比关系。
通过实验我们可以得出这样的结论:在线性边缘滤波解调法中,电压比值θ与悬臂梁末端位移x成正比关系,x=93.30θ—17.43。
4.2 振动试验
将标定的悬臂梁装置换为BZ8002等强度梁试验台。并对LabVIEW程序略微调整:将低通滤波器改为带通滤波器,截止频率由所设定电机转速的快慢决定,振动信号的频率由LabVIEW自带“信号的时间与瞬态特征测量”函数直接计算显示结果。图4所示为频率为50Hz,布拉格波长的变化过程。实验表明在振动频率小于1KHz,振幅在12~28mm范围内,测试系统具有较好的准确度和重复性。

图3 等腰悬臂梁装置结构示意图

图4 振动频率为50Hz时布拉格波长的变化
5. 结论
本文选用光纤波拉格光栅检测振动,具有抗干扰能力强、质量轻等优点;利用长周期光纤光栅的透射特性,设计了动态解调系统,该方法具有分辨率高、准确度高、体积小等特点;以LabVIEW为开发平台,实现了数据处理显示的功能。当振动频率小于1kHz,振幅在12~28mm范围内时,该测试系统具有较好的准确度和重复性。
* [1] 王宏亮,张晶,乔学光等.光纤光栅传感解调系统的研究进展[J].半导体技术,2007, 32(3):191
* [2] 饶云涛,王义平,朱涛.光源光栅原理及应用[M].北京:科学出版社,2006
* [3] 沈小燕,林玉池,付鲁华等.LabVIEW实现光纤光栅传感解调[J].传感技术报,2008, 21(1): 61—65.
