基于有效磁链滑模观测器的IPMSM直接转矩控制
2017-08-08张兴华刘伟
张兴华,刘伟
(南京工业大学电气工程与控制科学学院,江苏 南京 211816)
基于有效磁链滑模观测器的IPMSM直接转矩控制
张兴华,刘伟
(南京工业大学电气工程与控制科学学院,江苏 南京 211816)
提出了一种有效磁链滑模定子磁链观测器。与一般滑模磁链观测器不同的是该观测器并不包含转速自适应环节,从而避免了由于转速估计误差所导致的磁链观测性能下降。采用Lyapunov稳定性理论证明了观测器渐近收敛。通过实时估计有效磁链信息,间接计算出电机转速,从而实现内置式永磁同步电机(ΙPMSM)的无速度传感器直接转矩控制。仿真结果表明了该方法的有效性。
内置式永磁同步电机;有效磁链;滑模观测器;无速度传感器;直接转矩控制
自20世纪80年代德国学者Depenbrock和日本学者Takahashi提出直接转矩控制方法以来[1-2],该方法一直是电机驱动控制技术领域里的一个研究热点。与矢量控制通过坐标变换,控制定子电流的励磁分量和转矩分量来间接控制转子磁链和转矩不同,直接转矩控制是根据转矩和磁链误差,在定子坐标系中直接对转矩和磁链进行调节,无需进行复杂的坐标变换,具有控制结构简单、鲁棒性强和转矩动态响应快等优点。直接转矩控制最初只是应用于感应电机的控制,直到20世纪90年代末,才被用于永磁同步电机驱动控制[3-4]。
近年来,无速度传感器控制技术受到人们的广泛关注。由于省略了在电机转轴上安装速度传感器,不仅降低了驱动系统实现成本,而且能够减小系统体积,提高运行可靠性。无速度传感器控制系统中的转速估计方法主要有2种基本类型:1)基于反电动势检测的状态观测器[5-6];2)利用磁极凸性的高频信号注入方法[7]。
基于反电动势的状态观测器依据电机动态模型进行设计,在中高速区具有优良的性能,但在低速区,由于反电动势正比于电机转速,该方法的应用受到限制。此外,由于状态观测器是基于电机模型进行设计,其估计性能受电机模型参数变化的影响大;高频信号注入法是将高频旋转或脉冲电压信号注入定子绕组,利用转子磁极凸性,从高频电流响应信号中提取转子位置信息。该方法在电机低速运行区甚至零速时有很好的估计性能,其主要缺点是需额外增加高频信号源和设计合适的滤波器,系统实现的硬件和软件结构复杂。此外,注入的高频信号还会产生谐波转矩脉动,增加功耗。
目前,常用的基于反电动势检测的状态观测器的转速估计方法包括模型参考自适应观测器[8]和扩展的卡尔曼滤波器[9]等。这类估计方法的性能很大程度上依赖于电机模型参数。为降低参数变化和扰动对转速估计影响,人们将滑模变结构控制方法引入到无速度传感器电机驱动系统。由于滑模控制对干扰和摄动的不变性,当系统状态到达滑模面时,观测器将完全不受参数变化和负载扰动的影响,从而大大增强了驱动系统的鲁棒性[10-11]。
本文提出了一种内置式永磁同步电机的滑模磁链观测器。与以往的滑模观测器不同,该观测器的实现并不需要任何转速自适应机制,从而避免了由于转速估计偏差导致的磁链观测误差。通过引入有效磁链概念,在获得有效磁链的位置估计值后,可间接计算出转速。将设计的滑模观测器与内置式永磁同步电机直接转矩控制相结合,提出了一种基于有效磁链滑模观测器的内置式永磁同步电机无速度传感器直接转矩控制系统的实现方案。仿真结果表明,提出的滑模观测器能够精确给出转子和定子磁链信息。即使在电机低速运行时,观测器依然有良好的估计性能。
1 IPMSM的数学模型与有效磁链
1.1 IPMSM的数学模型
在转子磁链坐标系(d-q)中,ΙPMSM的电压方程为
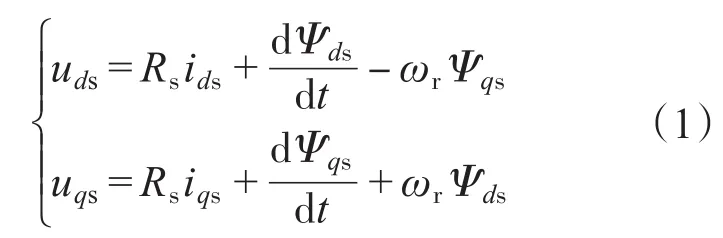
磁链方程为
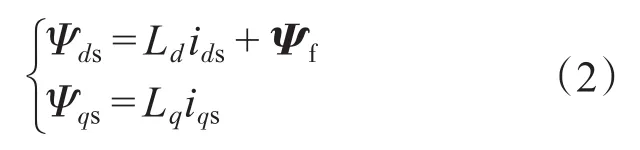
转矩方程为
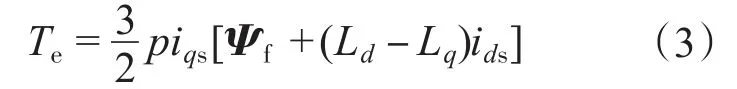
式中:uds,uqs,ids,iqs,Ψds,Ψqs分别为转子磁链坐标系中的定子电压、定子电流和定子磁链的d,q轴分量;Rs为定子电阻;ωr为转子电角速度;Ld,Lq为d,q轴电感;p为极对数;Ψf为转子永磁磁链。
1.2 有效磁链
定义有效磁链(active flux)Ψa为乘以1.5Piqs后等于电磁转矩的磁链值[12],即
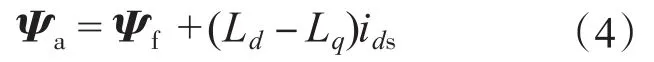
该有效磁链包括转子永磁体磁链和凸极磁链2部分,有效磁链矢量Ψa和定子磁链矢量Ψs、转子磁链矢量Ψf在静止坐标系(α-β)和转子磁链旋转坐标系(d-q)中的关系如图1所示。

图1 IPMSM的磁链矢量Fig.1 Flux linkage vectors of IPMSM
由图1可见,有效磁链矢量Ψa与转子磁链Ψf同向,即与旋转坐标系的d轴方向一致。由有效磁链的定义式(4)可得:

在静止坐标系(α-β)中可写成:
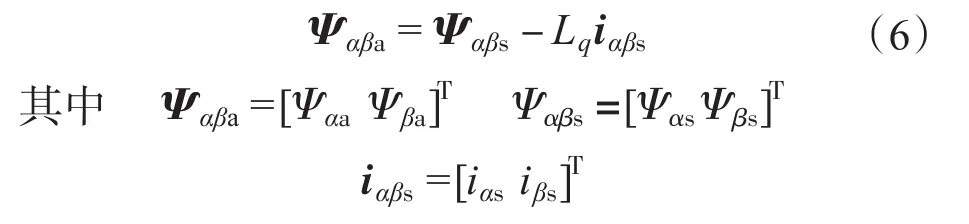
因此,转子位置角和定子磁链角的估计值和,可分别表示成:
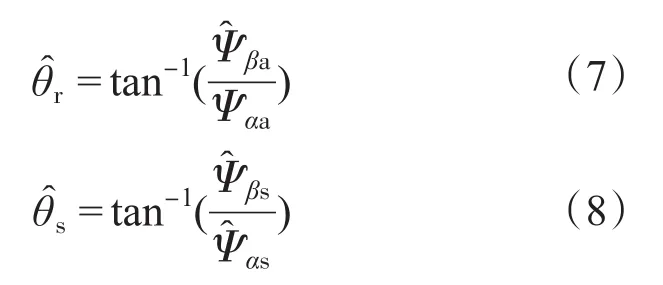
若能准确估计转子位置角,则对式(7)两边求导,可得如下的转子角速度估计值:

2 滑模磁链与转速观测器设计
2.1 滑模磁链观测器结构
根据静止坐标系下的电压方程:
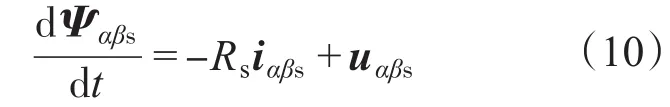
可构造定子磁链滑模观测器
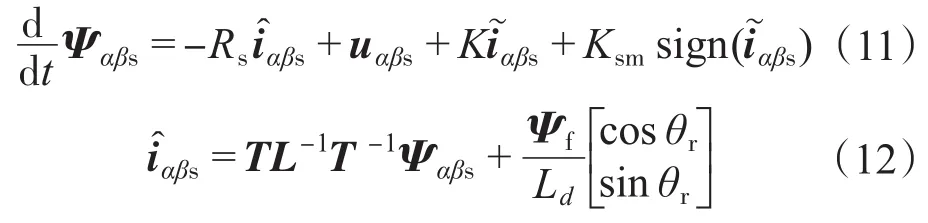
观测器方程式(11)右边包括1个线性Luenberger观测器反馈项,用于校正定子磁链估计值;1个符号函数项,用于改善观测器的鲁棒性。
图2所示为滑模磁链观测器的结构。

图2 滑模磁链观测器结构图Fig.2 Sliding-mode flux linkage observer
该观测器可以同时给出定子磁链和有效磁链的估计值,进而可由式(7)~式(9)得到转子位置角、定子磁链角和转速的估计值。转矩估计值可由下式计算得到:
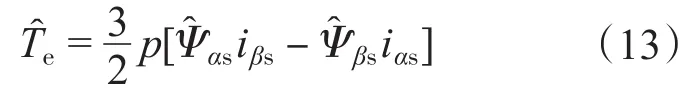
2.2 稳定性分析
由式(12)可得定子电流估计误差为
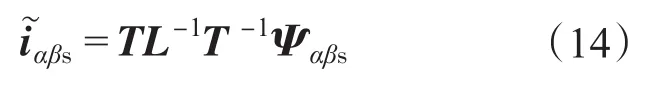
式(10)减去式(11),可得定子磁链误差动态方程:

定义如下的Lyapunov函数:

对V求导则有

将式(14)和式(15)代入式(17)有:

2.3 IPMSM无速度传感器驱动控制系统的实现
图3所示为基于滑模磁链观测器的ΙPMSM无速度传感器直接转矩控制系统结构图。以下对其主要功能模块的实现进行详细的说明。

图3 IPMSM的无速度传感器控制系统结构图Fig.3 Speed-sensorless control system of IPMSM
图3中的MTPA(maximum torque per ampere)是最大转矩电流比控制模块,其功能是计算在一定的电机运行工况下,使Te/is最大的定子磁链参考值。在满足MTPA控制条件时有[12]:
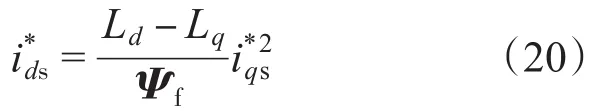
将式(20)代入式(3)可得:
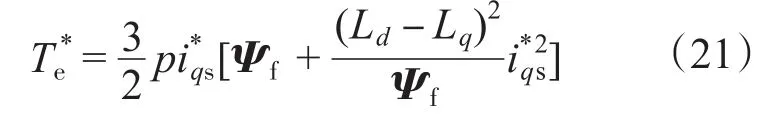

利用式(22)及式(20)、式(2)可计算出在MTPA控制策略下,给定参考转矩T*e后的定子磁链参考值Ψ*s。
图3中静止坐标系(α-β)中的定子电流iαβs由测得的相电流ia和ib经3/2变换后得到;定子电压uαβs先由测得的直流母线电压Udc和逆变器开关状态(Sa,Sb,Sc)计算得到三相电压ua,ub,再经3/2变换后得到定子电流iαβs和定子电压uαβs,作为滑模观测器的输入量。控制系统内环转矩控制器和定子磁链控制器均为滞环比较器,其输入分别是转矩误差 ΔTe=T*e-Te和磁链误差ΔΨs=Ψ*s-Ψs,输出是逻辑变量CT和CΨ,CT=1表示实际转矩小于参考转矩,反之CT=0则表示实际转矩大于参考转矩。对于磁链控制,CΨ取值有同样的含义。这2个逻辑变量与表示定子磁链矢量所处扇区的变量θ(i),(i=1,2,…,6)共同作为开关逻辑表的查表变量,通过查表来确定逆变器的开关状态(Sa,Sb,Sc),即所需的电压矢量Ui(i=1,2,3,4,5,6;不用零矢量U0,U7)。表1是逆变器开关逻辑表,定子磁链所处空间区域及逆变器开关状态所对应的电压矢量如图4所示。

表1 逆变器开关逻辑表Tab.1 Switching states for the inverter

图4 空间电压矢量Fig.4 Space voltage vectors
3 仿真结果
为验证本文提出的定子磁链与转速估计方法的有效性,采用Matlab/SimPowerSystems建立了系统仿真模型。
仿真中采用的ΙPMSM电机参数为:额定功率PN=1.3 kW,额定转速nrN=2 500 r/min,极对数np=4,直轴电感Ld=7.66 mH,交轴电感Lq= 17 mH,转子永磁磁链Ψf=0.158 Wb,转子惯量J=0.008 kg·m2,定子电阻RsN=1.35Ω,粘滞摩擦阻尼系数B=0.001,输出转矩额定值TeN=5 N·m。设置转矩滞环控制器的带宽为ΔTb=0.1 N·m,磁链滞环控制器的带宽ΔΨb=0.01 Wb,PWM采样周期Ts=100 μs,定子磁链观测器的滑模增益Ksm=0.001,定子磁链给定值采用MTPA计算。转速控制器参数Kp=0.2,Ki=10,输出转矩限幅Temax=±5N·m,转速控制周期取为10Ts。
图5是转速初始给定值为n*r=1 000 r/min,1 s时转速再跳变为n*r=-1 000 r/min时的控制仿真曲线。电机运行时空载启动,0.5 s时突加TL=2 N·m的负载,1.5 s负载变为TL=-2 N·m。图5中从上至下依次为定子相电流、转速和转矩。可见,电机启动时直接转矩控制系统的转矩动态响应很快,转速上升平稳,转速控制的稳态误差较小,当负载发生跳变时,电机的转速波动较小。滑模观测器可以很好地估计定子磁链和转速信息,驱动系统的控制性能优良。
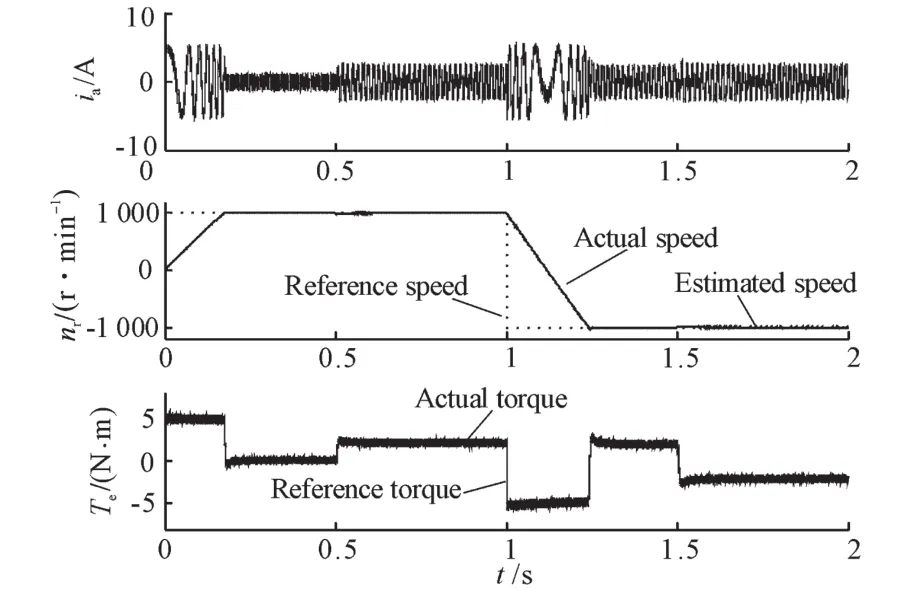
图5 中速区运行的控制仿真结果Fig.5 Simulation results in medium speed range
图6是低速运行时的控制仿真结果。电机空载启动,转速初始给定值n*r=10 r/min,0.5 s时跳变为n*r=-10 r/min,0.3 s时突加TL=1 N·m的负载,0.6 s时突加TL=-1 N·m的负载。从中可见,驱动系统在低速时依然有良好的控制性能,从而验证了该方法的有效性。

图6 低速区运行的控制仿真结果Fig.6 Simulation results in low speed range
4 结论
提出了一种内置式永磁同步电机直接转矩控制系统的滑模磁链与转速观测器设计方法。以定子电流估计误差构成滑模面,采用Lyapunov稳定性理论证明了观测器渐近收敛。该观测器可以在宽调速范围内提供精确的磁链与转速估计值,且对电机参数变化和负载扰动具有较强的鲁棒性。
[1]Takahashi I,Naguchi T.A New Quick-response and High-effi⁃ciency Control Strategy of an Induction Motor[J].IEEE Trans⁃actions on Industry Applications,1986,22(5):820-827.
[2]Depenrock M.Direct Self-control of Inverter-fed Machine[J].IEEETransactionsonPowerElectronics,1988,3(4):420-429.
[3]Zhong L,Rahman M F,Hu W Y,et al.Analysis of Direct Torque Control in Permanent Magnet Synchronous Motor Drives[J].IEEETransactionsonPowerElectronics,1997,12(3):528-536.
[4]Zhong L,Rahman M F,Hu W Y,et al.A Direct Torque Control⁃ler for Permanent Magnet Synchronous Motor Drives[J].IEEE Transactions on Energy Conversion,1999,14(3):637-642.
[5]Fabio Genduso,Rosario Miceli,Cosimo Rando,et al.Back EMF Sensorless-control Algorithm for High-dynamic Perfor⁃mance PMSM[J].IEEE Transactions on Industrial Electron⁃ics,2010,57(6):2092-2100.
[6]Shinji Ichikawa,Mutuwo Tomita,Shinji Doki,et al.Sensor⁃less Control of Synchronous Reluctance Motors Based on Ex⁃tended EMF Models Considering Magnetic Saturation with On⁃line Parameter Identification[J].IEEE Transactions on Indus⁃try Applications,2006,42(5):1264-1274.
[7]王莉娜,郝强.基于高频方波信号注入的PMSM无传感器低速运行研究[J].电气传动,2015,45(6):20-25.
[8]Khlaief A,Boussak M,Chaari A.A MRAS-based Stator Resis⁃tance and Speed Estimation for Sensorless Vector Controlled IPMSM Drive[J].Electric Power Systems Research,2014(3): 1-15.
[9]Shehata E G.Speed Sensorless Torque Control of an IPMSM Drive with Online Stator Resistance Estimation Using Re⁃duced Order EKF[J].International Journal of Electrical Pow⁃er&Energy Systems,2013,47(5):378-386.
[10]Xu Zhuang,Rahman M F.An Adaptive Sliding Stator Flux Ob⁃server for a Direct-torque-controlled IPM Synchronous Motor Drive[J].IEEE Transactions on Industrial Electronics,2007,54(5):2398-2406.
[11]Gilbert Foo,Rahman M F.Sensorless Sliding-mode MTPA Control of an IPM Synchronous Motor Drive Using a Slid⁃ing-mode Observer and HF Signal Injection[J].IEEE Trans⁃actions on Industrial Electronics,2010,57(4):1270-1278.
[12]Ion Boldea,Mihaela Codruta Paicu,Gheorghe-Daniel Andrees⁃cu,etal."Activeflux"DTFC-SVMSensorlessControlofIPMSM[J].IEEE Transactions on Energy Conversion,2009,24(2): 314-322.
Direct Torque Control of Interior Permanent Magnet Synchronous Motors Based on Sliding-mode Active Flux Observers
ZHANG Xinghua,LIU Wei
(College of Electrical Engineering and Control Science,Nanjing Tech University,Nanjing 211816,Jiangsu,China)
A sliding-mode observer based on"active flux"concept was proposed.Different from the conventional stator flux linkage observer,this observer was not consisted of the speed adaptive loop.Therefore,it was immune to estimate of speed error which would make the performance of the observer worsen.The Lyapunov stability theory was employed to prove that the observer was asymptotically stable.By using the estimated active flux angle,the motor speed could be calculated.As a result,the speed sensor-less IPMSM direct torque control drive was achieved.Simulation results are presented to validate the effectiveness of the proposed method.
interior permanent magnet synchronous motor;active flux;sliding-mode observer;speed sensor-less;direct torque control
TP273
A
10.19457∕j.1001-2095.20170702
2016-06-27
修改稿日期:2016-09-29
国家自然科学基金(51477073);江苏省自然科学基金(BK20161549)
张兴华(1963-),男,博士,教授,Email:zxhnjut@163.com
