并联型有源电力滤波器的复合电流控制方法
2017-08-08田飞燕高云广宋建成郑丽君杨健康康勤根
田飞燕,高云广,2,宋建成,郑丽君,杨健康,康勤根
(1.煤矿电气设备与智能控制山西省重点实验室(太原理工大学),山西 太原 030024;2.太原科技大学电子与信息工程学院,山西 太原 030024;3.山西晋城无烟煤矿业集团有限责任公司,山西 晋城 048000)
并联型有源电力滤波器的复合电流控制方法
田飞燕1,高云广1,2,宋建成1,郑丽君1,杨健康3,康勤根3
(1.煤矿电气设备与智能控制山西省重点实验室(太原理工大学),山西 太原 030024;2.太原科技大学电子与信息工程学院,山西 太原 030024;3.山西晋城无烟煤矿业集团有限责任公司,山西 晋城 048000)
针对非线性负荷对电网电能质量的影响,研究一种并联型有源电力滤波器拓扑结构。根据此拓扑结构,建立其在三相静止坐标系下和两相同步旋转坐标系下的数学模型,推导模型的传递函数,设计基于PΙ控制的电流控制器。通过分析PΙ控制器在有源电力滤波器电流跟踪控制中存在的局限性,提出将PΙ控制与重复控制并联的复合控制策略,以改善系统的稳态性能。通过实验对所提出的控制方法进行研究,结果表明该复合控制方法具有很高的稳态补偿精度,能够有效地抑制由非线性负载引起的谐波电流,大大改善电网电流波形。
谐波治理;有源电力滤波器;PΙ控制;重复控制;复合控制
随着电力电子装置的普遍应用,大量的谐波和无功电流注入到电网中[1],导致各种电力设备无法正常工作,甚至会引起设备损坏和事故发生。因此谐波治理技术的研究被广泛关注。
目前,有源电力滤波技术受到广泛的研究。有源电力滤波器(active power filter,APF)能够抵消电网中由非线性负载引起的谐波和无功电流,改善电网电流波形。与无源滤波器相比,APF占用空间小,不受电网阻抗的影响,能够有效跟踪频率和幅值均变化的谐波电流,并且还可以消除滤波器阻抗和网络阻抗之间可能存在的谐振[2-4]。
有源电力滤波器是通过控制逆变器的输出电流来快速地跟踪由非线性负载引起的谐波电流,实现对谐波电流的有效补偿。在此过程中,要使逆变器的输出电流快速精确地跟踪上谐波电流的变化,关键在于电流跟踪控制算法的实时性和有效性。电流跟踪控制方法主要有:滞环比较控制、三角载波控制、无差拍控制等。其中三角载波控制较为简单易行,且动态响应好、开关频率固定,其将电流的偏差经放大器后再与三角波比较,比较所得的矩形脉冲作为控制信号来控制逆变器的开关元件。放大器通常采用PΙ控制器,而PΙ控制只有当给定是直流量时才能实现系统的无静差跟踪[5-7]。因为有源电力滤波器控制的给定值是含有多次谐波的交流量,因此,单独PΙ控制无法对谐波信号实现无静差跟踪。
本文在传统PΙ控制的基础上,结合重复控制思想,提出将PΙ控制和重复控制相结合的电流控制方法,以提高APF的补偿性能,降低电网电流的总谐波失真(total harmonics distortion,THD)。
1 APF数学模型及控制系统
系统主要有3部分:电源、非线性负载和APF。其中APF包括:电压源逆变器、直流母线电容和三相输出电感。图1所示为三相并联型有源电力滤波器的结构原理图,主电路为三相电压型PWM变换器,非线性负载为带阻性负载的三相不控整流桥。

图1 SAPF系统原理图Fig.1 The system schematic of three-phase SAPF
1.1 APF数学模型
由图1可得,三相有源电力滤波器在三相坐标系下的数学模型为
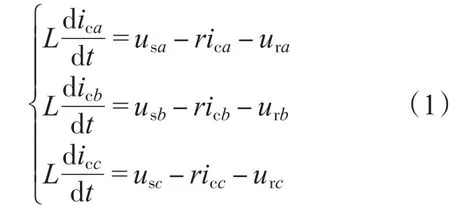
式中:usa,usb,usc为电网电压;ura,urb,urc为PWM变换器输出电压;ica,icb,icc为补偿电流;r为输出电感及开关损耗的等效电阻。
为了便于对有功和无功分量进行独立控制,将式(1)通过abc/dq坐标变换,转换到d-q坐标系中,下式即为APF在d-q坐标系中的数学模型:

根据此模型即可以进行PΙ控制器的设计。
1.2 APF的控制系统
在有源滤波器的控制中,不仅需要对电流进行快速地跟踪和补偿,而且还需对PWM变换器直流侧电压进行稳定控制,以维持系统特有的稳定性。根据补偿电流快速性要优于直流侧电压控制的特点,采用电压外环电流内环的控制方法。
图2是SAPF控制结构图,电压环采用PΙ控制,其作用是保证APF的直流侧电压稳定在给定值,使电流内环能够有效地补偿谐波[8-11]。本文所研究的电流环控制器为PΙ控制器和复合控制器,电流环的作用是控制APF输出与给定谐波电流大小相等方向相反的电流。

图2 SAPF控制结构图Fig.2 Control structure diagram of SAPF
2 传统PI控制方法
由式(2)可知,d,q轴变量之间相互耦合,为了简化控制器设计,可采用带有电压前馈和输出电流交叉解耦项的PΙ控制器。urd,urq的控制方程如下:
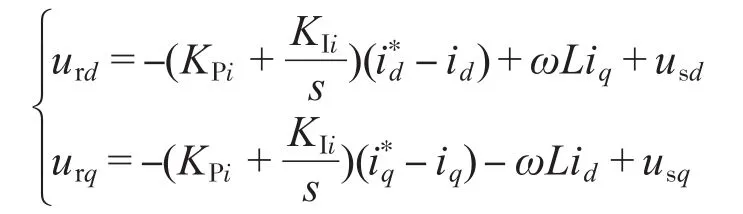
将式(3)带入式(2)可得:

式中:KPi为电流内环比例系数;KIi为积分系数;i*d,i*q分别为id,iq的谐波电流给定值。
从式(4)可以看出,通过控制i*d-id和i*q-iq可以对id,iq进行独立控制。由式(4)可知,控制对象实际上是一阶惯性环节。图3为采用PΙ控制器对电流进行调节时,电流环的简化控制框图。

图3 d-q坐标系下的电流环简化控制图Fig.3 Simplified current control block diagram of APF in d-q frame
根据图3可知,电流闭环控制系统传递函数为
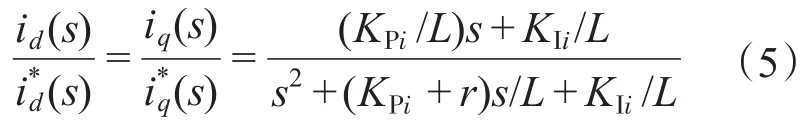
采用零极点对消法,即令

则式(5)可以简化为

式中:Td为d,q轴电流闭环系统电流响应延时时间常数。

由式(8)可知,Td与电流控制器的比例系数KPi成反比,与输出电感L成正比。当电感一定的情况下,若增大KPi,则延时时间会减小。但是KPi不能无限制地增大,过大的KPi会导致系统振荡。单独的PΙ控制在控制谐波电流时受到带宽范围的限制,难以消除指令延迟的影响,补偿效果不理想。
3 APF复合控制器设计
针对有源电力滤波器电流环单独PΙ控制补偿性能有限,本文提出基于PΙ控制和重复控制的复合控制系统来满足系统对稳态性能的要求。重复控制的基本思想源于控制理论中的内模原理,即把系统外部信号的动态模型植入控制器内,在稳定的闭环系统中包含外部输入信号的数学模型,以构成高精度的反馈控制系统[11-13]。
在有源电力滤波器中,给定信号为检测到的谐波交流信号,其由许多不同频率的交流量叠加而成。若要实现无差跟踪,则要求控制模型中的内模能够构建出每一种交流信号。虽然检测到的谐波信号含有很多不同频率的交流量,但是在每一个基波周期谐波信号的波形都是重复出现的。因此,可以将基波周期作为这些谐波信号的重复周期。
3.1 APF重复控制器的内模
图4为APF重复器内模,其中N=T/Ts,T为基波周期,Ts为控制器离散过程中的采样周期,z-N为纯延时环节。

图4 重复信号发生器内模模型Fig.4 Internal model of repetitive signal generator
从图4可以得到y(z)和e(z)的关系,如下式:
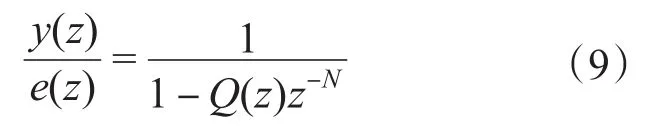
由式(9)可以看出,每隔1个周期(N步),则将上周期输出量的削弱值与当前的输入量累加,该累加值作为当前周期的输出。根据谐波的周期性特点,采用重复控制可以提高跟踪信号的准确性和稳定性。
3.2 APF重复控制器结构
图5是重复控制器结构,其中P(z)为控制对象,要求其本身是稳定的;Q(z)和C(z)分别为重复控制辅助补偿器和针对受控对象的补偿器,C(z)=KrzkS(z),Kr为重要控制器增益,k为相位补偿系数;r为需要跟踪的重复性指令。重复控制器检测指令r与实际输出y之间的误差e,内模对误差e进行周期性积分,以便在误差消失或变得较小时控制器仍能输出相应的控制量。在周期延迟环节和补偿器的作用下,根据内模积分的结果,重复控制器将在下一周期的适当时刻输出控制量ur,以减小误差e。

图5 重复控制器结构Fig.5 The structure of the repetitive controller
3.3 APF复合控制策略
重复控制器对误差信号是以基波周期为步长进行的累加,它无法将动态响应时间减小到1个基波周期内。而PΙ控制策略动态响应速度很快,因此将传统PΙ控制策略和重复控制策略并联使用,构成新的控制系统,同时兼顾系统的稳态性能和动态性能。复合控制框图如图6所示。
图6中,GPI(z)是PΙ控制器,通过对控制对象进行频域分析并校正,可得到PΙ控制下稳定运行参数。在PΙ控制的稳定系统下,重复控制器的参数具体计算步骤如下:
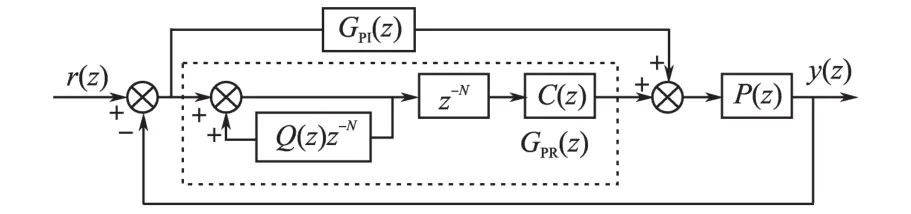
图6 PI控制和重复控制的并联式复合控制框图Fig.6 Parallel compound control block diagram of the PI control and repetitive control
1)计算1个周期的采样次数N;
2)选取Q(z)。Q(z)=1时,重复控制系统的稳态误差可达到零,但是要使系统保持稳定,则必须有Q(z)<1。考虑稳定性和稳态误差两方面的要求,Q(z)取常数为0.98;
3)S(z)由控制对象的幅频特性选择,一般补偿器S(z)可选二阶低通滤波器。当补偿50次以内的谐波电流时,截止频率设为fc=2 800 Hz,则所设计的二阶低通滤波器:

4)为了简化,设计k估算值为3即z3,主要作用是补偿S(z)和控制对象在中低频段的相位滞后;
5)Kr越小系统稳定性越好,但收敛速度变慢且稳态误差上升,Kr通过实验选取为0.7。
4 实验结果
为了验证上述控制策略的有效性,在实验室搭建了APF实验平台进行特性实验。实验系统主要包括3部分:电源系统、三相二极管整流装置和并联型有源电力滤波器。不控桥负载电阻为20 Ω,并联型有源电力滤波器的系统组成框图如图7所示。

图7 并联型有源电力滤波器系统组成框图Fig.7 Diagram of shunt active power filter system
主电路ΙGBT参数为100 A/1 200 V,控制器DSP采用TΙ公司的TMS320F28335,谐波测量仪器采用Fluke公司的Fluke434电能质量分析仪,HDO6104示波器以及Tektronix P5210电压测量探头和HOKΙ 3274电流测量探头等。APF实验主要参数为:电源相电压110 V,电网频率50 Hz,APF输出电感2 mH,APF直流侧电容3 300 μF,APF直流侧电压110 V,开关频率9 kHz。
4.1 实验波形
图8为负载(带阻性负载的三相不控整流桥)电流波形频谱分布情况,单独采用PΙ控制器时得到的电网电流频谱和波形如图9和图10所示。

图8 负载电流波形频谱图Fig.8 Spectrum waveform of load current
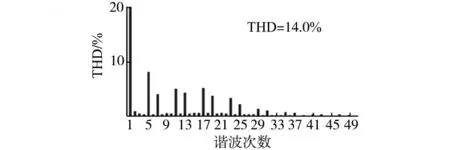
图9 PI控制补偿后电网电流频谱图Fig.9 Spectrum waveform of grid current with PI controller

图10 单独PI控制时电流波形Fig.10 Current waveforms with PI controller
采用PΙ与重复控制相结合的复合控制策略对电流进行跟踪控制时,电网电流谐波分布及频谱如表1和图11所示,电流波形如图12所示。
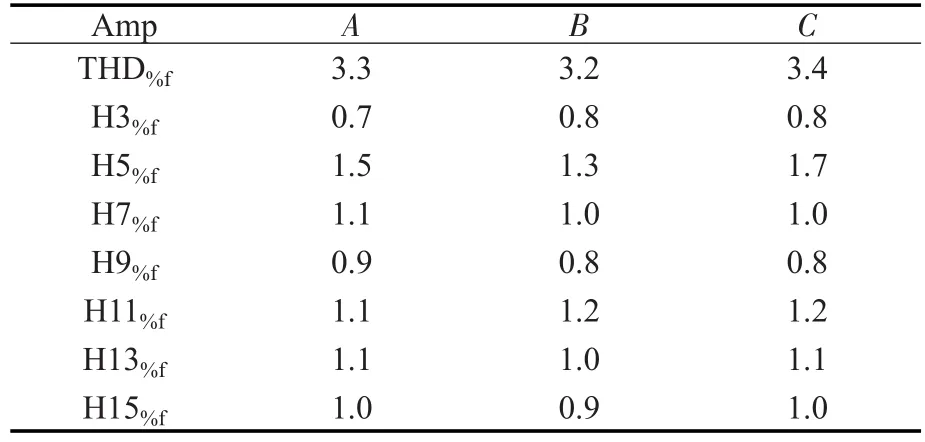
表1 复合控制补偿后电网电流谐波分布Tab.1 The harmonic distribution of grid current with compound controller

图11 复合控制补偿后电网电流频谱Fig.11 Spectrum waveform of grid current with compound control
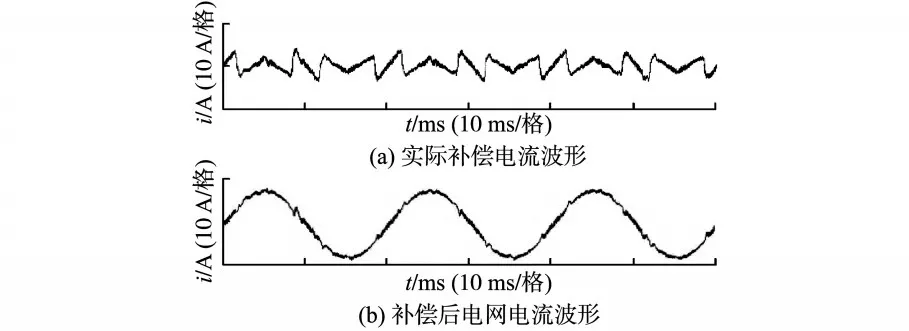
图12 复合控制时电流波形Fig.12 Current waveforms with compound control
4.2 实验结果分析
从图9可看到,采用PΙ控制进行补偿后,电网电流THD从28.6%降低到了14.0%,补偿效果不理想。这是由于在系统稳定的前提下PΙ控制的补偿能力有限,即PΙ控制器无法对交流信号实现无差调节。图10中补偿后的网侧电流波形有周期性尖脉冲出现,其原因是三相不控整流在换相时,一相电流瞬时发生跳变,在陡变的地方,电流频谱较为复杂,含有不确定的高频分量,导致检测到的电流指令超出电流环PΙ调节器能够控制的带宽范围。此外,数字控制中总有一拍延迟,APF无法实时地输出需要的谐波以抵消这些陡变量,造成实际系统电流波形上出现了这些尖脉冲。从图11和图12可以看出,采用PΙ+重复控制算法进行补偿后,网侧电流波形有明显改善,电流THD值降低到了3.3%。从图12可以看出,加入重复控制器后,电网电流波形的正弦度大大改善,在固定位置上的尖冲也得到了有效抑制,这是因为重复控制器实际上是一种以基波周期为步长对误差信号进行累加的积分控制,通过对波形误差进行逐周期的补偿,即可达到很高的稳态精度。
5 结论
本文针对非线性负荷对电网质量的影响,对非线性负荷特性、并联型有源滤波器的拓扑结构、数学模型、控制策略和特性试验进行了系统研究,研究结论如下:1)提出的将PΙ控制与重复控制并联使用的复合控制策略,有效解决了单独采用PΙ控制时补偿精度不高的问题,提高了系统稳态精度,实现了实时准确跟踪补偿电流的目的;2)设计了基于复合控制的并联型有源电力滤波器,有效抑制了由非线性负载引起的谐波电流。采用APF进行补偿后,电网电流波形正弦度大大提高,近似于正弦波,电流THD减小到5%以下,达到了谐波抑制的国家标准。
[1]王兆安,杨君,刘进军.谐波抑制和无功功率补偿[M].北京:机械工业出版社,2006.
[2]魏学良,戴珂,方昕,等.三相并联型有源电力滤波器补偿电流性能分析与改进[J].中国电机工程学报,2007,27(28):113-119.
[3]Chen B,Zha X,Gong J,et al.Realization and Improvement of Repetitive Control in Rotating Frame for Active Power Filter System[J].Applied Power Electronics and Exposion,2010:887-894.
[4]杨新华,谢斌.基于电流环复合控制的有源电力滤波器研究[J].电气传动,2014,44(2):55-58.
[5]Rshmani S,Hamadi A,AL-Haddad K.A Lyapunov-func⁃tion-based Control for a Three-phase Shunt Hybrid Active Fil⁃ter[J].IEEE Transactions on Industrial Electronics,2012,59(3):1418-1429.
[6]郭伟峰,武健,徐殿国,等.新型滑模控制的并联混合有源电力滤波器[J].中国电机工程学报,2009,29(27):29-35.
[7]魏学良.三相三线并联型APF电流环数字化控制研究[D].武汉:华中科技大学,2007.
[8]于晶荣,粟梅,孙尧.有源电力滤波器的改进重复控制及其优化设计[J].电工技术学报,2012,27(2):235-242.
[9]Asiminoaei L,Aeloiza E,Enjeti P N,et al.Shunt Active-pow⁃er-filter Topology Based on Parallel Interleaved Inverters[J].IEEE Transactions on Industrial Electronics,2008,55(3):1175-1189.
[10]Xie C,Wang Y,Zhong X,et al.A Novel Active Damping Method for LCL-filter-based Shunt Active Power Filter[C]∕∕IEEE In⁃ternational Symposium on Industrial Elcetronics,2012:64-69.
[11]宫金武,查晓明,陈佰锋.一种快速重复控制策略在APF中的实现和分析[J].电工技术学报,2011,26(10):110-117.
[12]许明夏,林平,张涛,等.有源电力滤波器重复控制方法的设计[J].电源学报,2012(2):16-20.
[13]刘飞,宫金武,彭光强,等.一种复合式重复控制在并联型有源电力滤波器设计中的应用[J].电工技术学报,2012,27(12):138-145.
[14]Zou Z,Wang Z,Cheng M,et al.Active Power Filter for Harmo⁃nie Compensation Using a Digital Dual-mode-structure Repeti⁃tive Control Approach[C]∕∕IEEE International Symposium on Power Electronics for Distributed Generation Systems,2012:161-166.
Compound Current Control Method for Shunt Active Power Filters
TIAN Feiyan1,GAO Yunguang1,2,SONG Jiancheng1,ZHENG Lijun1,YANG Jiankang3,KANG Qingen3
(1.Shanxi Key Laboratory of Coal Mine Electrical Equipment and Intelligent Control,Taiyuan University of Technology,Taiyuan 030024,Shanxi,China;2.School of Electronics and Information Engineering,Taiyuan University of Science and Technology,Taiyuan 030024,Shanxi,China;3.Shanxi Jincheng Anthracite Coal Mining Group Co.,Ltd.,Jincheng 048000,Shanxi,China)
Aiming at the influence of nonlinear load on the quality of power grid,a shunt active power filter(SAPF)topology was researched.According to this topology,the mathematical model of the SAPF was established in the three-phase static coordinate system and the two-phase d-q synchronous rotating coordinate system.The transfer function of the model was deduced,and the current controller based on PI control was designed.By analyzing the limitation of PI controllers in current tracking control for active power filters,a compound control strategy combining repetitive control with PI control was proposed to improve steady state performance of the system.Experimental results demonstrate that the current control method combining PI control method with repetitive control method has a high steady-state compensation accuracy.It is able to effectively suppress harmonic currents caused by nonlinear loads and greatly improve grid current waveform.
harmonics suppression;active power filter;PI control;repetitive control;compound control
TM72
A
10.19457∕j.1001-2095.20170713
2016-06-15
修改稿日期:2016-08-20
晋煤集团科技攻关项目(JSYJ-JSKF-2014-0050);山西省重点实验室开放课题(MEI-201501)
田飞燕(1991-),女,硕士,Email:feiy0218@163.com
