基于STM32四轴飞行平台

易 凡， 邓 方，张培健，滕璇璇

（武汉轻工大学 电气与电子工程学院，湖北 武汉430040）

基于STM32四轴飞行平台

易 凡， 邓 方，张培健，滕璇璇

（武汉轻工大学 电气与电子工程学院，湖北 武汉430040）

本设计以STM32F407为控制核心，四轴飞行器为载体。硬件上由飞控电路，电源管理，通信模块，动力系统，机架，云台伺服系统组成。算法上采用简洁稳定的四元数加互补滤波作为姿态解算算法，PID作为控制器，实现飞行，云台增稳等功能。具有灵活轻盈，延展性，适应性强好等特点。

四旋翼飞行器；STM32；捷联式惯性导航；四元数姿态解算

四轴飞行器是一种利用4个旋翼作为飞行引擎来进行空中飞行的飞行器。进入20世纪以来，电子技术飞速发展四轴飞行器开始走向小型化，并融入了人工智能，使其发展趋于无人机，智能机器人。在实际应用方面，四轴飞行器可以在复杂、危险的环境下可以完成特定的飞行任务，也可以用于监控交通，环境等。本设计主要研究了四轴飞行器的姿态结算和飞行控制，并设计制作了一架四轴飞行器，对关键传感器做了标定，并利用用matlab分析数据，设计算法，还进行了单通道平衡试验调试，进行试飞实验取得了一定的效果。

1 系统方案

本设计采用STM32F4作为核心处理器，该处理器内核架构ARM Cortex-M4，具有高性能、低成本、低功耗等特点。主控板包括传感器MPU6050电路模块、无线蓝牙模块、电机启动模块，电源管理模块等；遥控使用商品遥控及接收机。控制芯片捕获接收机的PPM命令信号，传感器与控制芯片之间采用IIC总线连接，MCU与电调之间用PWM传递控制信号。软件算法才用基于四元数的互补滤波解算姿态角，控制算法采用经典PID控制器控制云台舵机和四轴电机。图1为本设计总体框图。

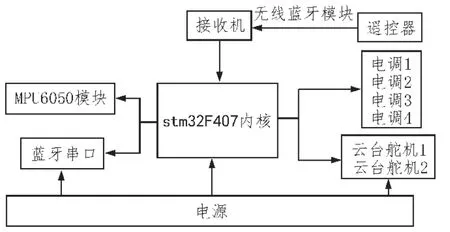
图1 系统总体框图

2 系统硬件设计

针对前面提出的整体设计方案，本设计采取模块化策略，将各个功能部分开来设计，最后组合起来。

表1 四轴飞行器硬件清单

3 系统软件设计

软件设计上由控制核心STM32F4读取传感器信息，解算姿态角，以姿态角为被控制量融合遥控信息后，输出到4个电机及两个舵机以完成四轴飞行控制和云台的稳定补偿。下图是软件流程：

图2 系统软件流程

3.1 四元素计算姿态角的实现

根据前面给出的姿态解算方程与四元数，即可得到姿态计算系统的计算原理如下图。

图3 姿态计算系统计算原理图

本设计基于互补滤波的思想上完成的四元素算法，其核心思路为利用加速度测得的重力向量与估计姿态得到重力向量的误差来矫正陀螺仪积分误差，然后利用矫正后的陀螺仪积分得到姿态角。

首先不妨设处理后的加速度数据为：ax，ay，az，单位 m/s^2。加速度计的向量为陀螺仪数据为：gx，gy，gz，单位 rad/s。 陀螺仪向量，由载体到导航坐标系的四元数形式转换矩阵为：。根据余弦矩阵和欧拉角的定义，地理坐标系的重力向量，转到机体坐标系，是中的第三列的3个元素。所以加速的向量与估计重力向量叉积：

然后利用向量的叉积，e→可视为误差向量，这个叉积向量仍旧是位于机体坐标系上的，而陀螺积分误差也是在机体坐标系，而且叉积的大小与陀螺积分误差成正比，正好拿来纠正陀螺。由于陀螺是对机体直接积分，所以对陀螺的纠正量会直接体现在对机体坐标系的纠正。用上面得到的结果校正陀螺仪：

此处k为一个常量系数。再利用二阶毕卡法解四元数微分方程，更新四元数为下一次计算做准备。毕卡二阶算法为：

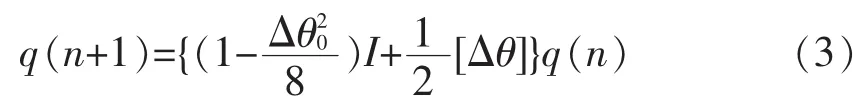
其中Δθ为角增量

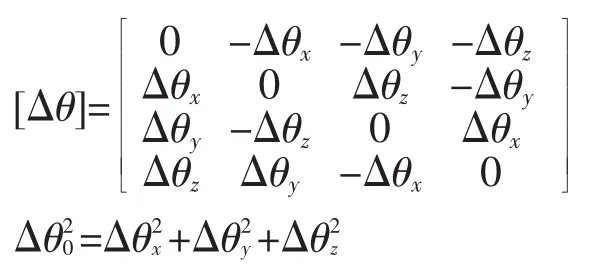
最后将四元数转变为欧拉角：

Q_ANGLE.Pitch=asin（-2*q1*q3+2*q0*q2）

Q_ANGLE.Rool=atan2（2*q2*q3+2*q0*q1-2*q）

Q_ANGLE.Yaw=atan2（2*q1*q2+2*q0*q3，-2*q2*q2-2*q3*q3+1）

通过以上算法本文成功得出了飞行器的姿态角，在开启电机的情况下，角度误差在+/-2°以内，满足了控制要求。姿态计算效果如下图所示，其中红色和蓝色是直接由加速度计算出的俯仰角和横滚角，青色和黄色为姿态结算后的俯仰角和横滚角。由图中数据可看出，解算的姿态角不仅能即时的反应角度变化切曲线平滑，说明姿态解算算法有效。

3.2 控制设计

由于四轴飞行器独特的机械结构，即结构上的对称设计，使得四轴在俯仰角的控制欲横滚角的控制上有这近乎相同的控制特性，且两者相对独立。四轴飞行器的俯仰，横滚，偏航，升降可以通过四个输入量来控制。通过设定一个期望角度，调整电机转速，使得测得的姿态角稳定在期望角。控制律的设计主要采用是闭环控制。以姿态角作为被控制量，采用经典的PID控制算法。四轴飞行器系统是一个时变且非线性的系统，采用传统PID算法的单一的反馈控制会使系统存在不同程度的超调和振荡现象，无法得到理想的控制效果。文中将前馈控制引入到了四轴飞行器系统的控制中，有效地改善了系统的实时性，提高了系统的反应速度；并且根据四轴飞行器系统的特点，对数字PID算法进行了改进，引入了微分先行环节，改善了系统的动态特性；使得控制器能够更好地适应四轴飞行器系统的实际情况。在姿态角的控制中，本设计将控制器捕获到的遥控器信号转换为一个角度，作为期望角，与解算出来的测量角作差，得到偏差error。将error乘以一个比例系数kp。在只有kp作用下，系统会有静差所以考虑利用积分ki控制消除稳态误差。但积分控制会降低系统的动态性能，甚至造成闭环系统不稳定，因此要对积分进行限幅，防止积分过大。对于微分，如果采用传统的D方法，在人为操纵四轴时会产生输入的设定值变化频繁且幅度较大，从而造成系统的振荡。对人为控制十分不利，为了解决设定值的频繁变化给系统带来的不良影响，本文在姿态角控制上引入了微分先行PID算法，其特点是只对输出量进行微分，即只对陀螺仪角速度测量值进行微分，而不对姿态角的设定值进行微分。这样，在设定值发生变化时，输出量并不会改变，而被控量的变化相对是比较缓和的，这就很好地避免了设定值的频繁变化给系统造成的振荡，明显地改善了系统的动态性能。控制周期定为4 ms，姿态控制系统示意图如下：

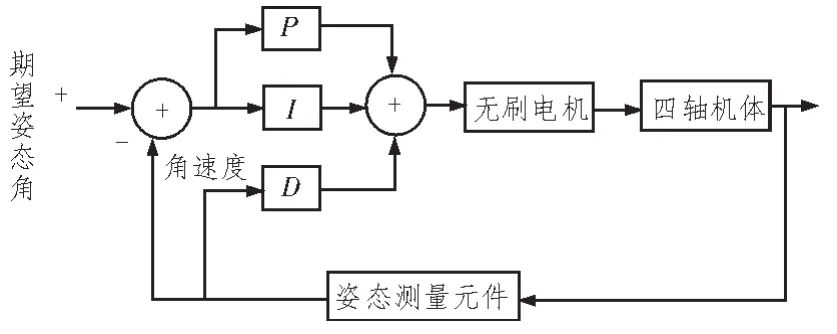
图4 姿态控制系统示意图

通过前面一章的介绍我们已经的达到了俯仰，横滚，航向3个控制量，然后将它们分别输入3个独立的如上图所示的PID控制器，我们可以得到3个PID 输出：pid_roll，pid_pitch，pid_yaw 将这 3 个输出量做简单的线性运算输出给电机。部分代码如下：

3.3 PID参数调节

1）确定比例增益P

确定比例增益P时，首先去掉PID的积分项和微分项，一般是令Ti=0、Td=0（具体见PID的参数设定说明），使PID为纯比例调节。输入设定为系统允许的最大值的60%～70%，由0逐渐加大比例增益P，直至系统出现振荡；再反过来，从此时的比例增益P逐渐减小，直至系统振荡消失，记录此时的比例增益P，设定PID的比例增益P为当前值的60%～70%。比例增益P调试完成。

2）确定积分时间常数Ti

比例增益P确定后，设定一个较大的积分时间常数Ti的初值，然后逐渐减小Ti，直至系统出现振荡，之后在反过来，逐渐加大Ti，直至系统振荡消失。记录此时的Ti，设定PID的积分时间常数Ti为当前值的150%～180%。积分时间常数Ti调试完成。

3）确定积分时间常数Td

积分时间常数Td一般不用设定，为0即可。若要设定，与确定 P和Ti的方法相同，取不振荡时的30%。

4）系统空载、带载联调，再对PID参数进行微调，直至满足要求。

最终调试好的标准应该是，PID输出曲线在有一个阶跃响应来是，响应一大一小两个波，小波是大波的四分之一。

3.4 调试与实验

在完成控制器底层的硬件驱动后，开始姿态角算法的调试。利用蓝牙模块将解算出的姿态角数据发回上位机，摇动四轴机体，观察上位机数据曲线与姿态演示立方块。

图中①和②为直接由加速度计算出的俯仰与横滚角，③和④为姿态解算后的姿态角，可明显看出直接由加速度计算出的姿态角噪声大，不平滑，不能真实反映姿态角的变化。而由四元数算法解算后的姿态角反应快，噪声小，足以满足控制要求。光观察曲线并不直观，还可以观察上位机中的立方块，当小立方块的姿态与四轴机体能够保持一致变化时说明姿态解算良好。通过以上手段可知姿态角解算满足需求。

图6 用于演示姿态的上位机立方块

4 结 论

当前面的各项调试都完成了之后，就准备要进行试飞实验。将4种飞行器放在水平地面上，开始启动姿态初始化程序，听到电调提示音后，缓慢增加油门，螺旋桨转速上升，将飞机拉离地面。由实际情况可看出当姿态发生倾斜时，姿态解算及PID控制能够及时调整电机转速，稳定飞行姿态。飞行器还能根据遥控指令的变化完成相应的动作。本此设计的四轴飞行器可实现垂直升降的要求，能保持姿态的稳定，机体晃动小，在微风的干扰下能够自动调整姿态，确保平稳飞行，且系统响应快，续航时间大概在8分钟。因此本次的设计是有效的。

[1]全国大学生电子设计竞赛组委会.全国大学生电子设计竞赛获奖作品精选[M].北京：北京理工大学出版社，2013.

[2]李俊.四轴飞行器的动力学模型及PID控制[J].辽宁工程技术大学学报：自然科学版，2012，31（1）：114-117.

[3]岳基隆．微小型四旋翼无人机研究进展及关键技术浅析[J].电光与控制，20l0，17（10）：46-52.

[4]刘峰，吕强，等．四轴飞行器姿态控制系统设计[J].计算机测量与控制，2011，19（3）:583-585.

[5]张东伟，张晓斌，郑先成.基于MP0566的飞机电源控制器系统设计[J].机械与电子，2010（6）:84-86.

[6]刘杰.四轴飞行器研究与设计[D].南京邮电大学，2013.

[7]解伟，张晓斌，张朋松，等.飞机电源控制器PCU测试仪的设计与实现[J].计算机测量与控制，2010，18（9）2207-2209.

[8]陆伟男，蔡启仲，李刚，等.基于四轴飞行器的双闭环PID控制[J].科学技术与工程，2014，14（33）：127-133.

[9]徐华中，余飞，何家俊，等.卡尔曼滤波在四轴飞行器导航中的应用[J].武汉理工大学学报，2012，34（3）:265-267.

[10]关萍萍，翟正军，姜红梅，等.基于LabWindows/CVI测控系统通用报表的设计与实现[J].计算机工程与设计，2010，31（1）:203-205.

[11]孙骅.基于GPS和AHRS的四轴飞行器悬停算法研究[J].机械科学与技术，2013，32（4）：481-487.

[12]王楠楠.不确定非线性系统的输出反馈控制[D].曲阜:曲阜师范大学，2010.

[13]王东来，吕强，刘峰，等.小型四轴飞行器动力学参数测定方法设计 [J].科技导报，2011，29（36）：42-45.

[14]成怡，金海林，修春波，等.四轴飞行器组合导航非线性滤波算法[J].计算机应用，2014（A01）:341-344.

[15]庞庆霈.四旋翼飞行器设计与稳定控制研究[D].合肥:中国科学技术大学，2011.

Four-rotor aircraft platform based on the STM32

YI Fan，DENG Fang，ZHANG Pei-jian，TENG Xuan-xuan
（School of Electric and Electronic Engineering ，Wuhan Polytechnic University，Wuhan 430040，China）

This design ，using a STM32F407 as the control core，uses a four-rotor aircraft as the carrier.Hardware consists of flight control circuit，power management，communication module，power system，aircraft frame，cloud deck.In algorithmic concept，the design uses the concise stable quaternion and complementary filter as a gesture decoding algorithm，taking PID as a controller to realize flight adjustments and other functions.The designer possesses qualities of flexible lightsome，ductility，good adaptability.

quad rotor； STM32； strap down inertial navigation； quaternion pose calculation

TN79

：A

：1674－6236（2017）14-0179-04

2016-06-07稿件编号：201606057

易 凡（1995—），男，湖北武汉人。研究方向：信号与信息处理、计算机测控。