玄碳混杂增强树脂基复合材料混杂比优化设计

徐 虹， 卢 岩， 张 可， 刘 栓， 王祥辉， 窦艳丽

(吉林大学 材料科学与工程学院，长春130025)



玄碳混杂增强树脂基复合材料混杂比优化设计

徐 虹， 卢 岩， 张 可， 刘 栓， 王祥辉， 窦艳丽

(吉林大学 材料科学与工程学院，长春130025)

对碳纤维-玄武岩纤维混杂增强树脂基复合材料最优混杂比范围进行研究。以碳纤维与玄武岩纤维平纹织物为增强体，制备9种具有不同混杂比的混杂纤维复合材料(Hybrid Fiber Reinforced Polymer，HFRP)试样，并进行拉伸实验。依据平纹织物结构特点，计算得出平纹织物单胞性能参数，在ANSYS中，以SHELL181壳单元体建立HFRP有限元模型。该模型对试样刚度的模拟值与实验值近似。分析模型受力时的应力云图发现，存在将HFRP破坏形式分为一次破坏与二次破坏的临界混杂比。有限元模拟研究树脂含量为45%时，不同混杂比的HFRP刚度、强度和拉伸极限应变。当混杂比为60%时，可保证HFRP强度无折减的情况下，较玄武岩复合材料(Basalt Fiber Reinforced Polymer，BFRP)刚度提高93.4%，较碳纤维复合材料(Carbon Fiber Reinforced Polymer，CFRP)拉伸极限应变提高11.3%。

混杂纤维复合材料；碳纤维；玄武岩纤维；平纹织物；混杂比

轻质高强型复合材料是航空航天、汽车、船舶、化工、电子和建筑等领域都极其需要的。纤维增强树脂基复合材料是其中应用范围最广、最具研究意义的一种。美国波音公司、欧洲空客集团已大力开展CFRP在民用飞机上的应用，波音787的CFRP用量高达50%，波音B767油耗降低17%[1-3]。

混杂纤维复合材料(HFRP)最早被日本的Hayashi[4]提出，认为其可综合两种、甚至多种纤维性能上的优点。有关HFRP最为典型的研究为掺杂玻璃纤维来改善碳纤维的断裂韧性。但近期发现，玻璃纤维对人体危害极大，不宜再大量生产应用。玄武岩纤维力学性能优良，适宜与碳纤维混杂，但相关研究较少[5-6]。

近年来，国内外学者对HFRP力学性能的改进主要通过对混杂比与铺层结构进行设计。为得出HFRP的强度与刚度，除测试方法外，还有很多学者依靠混合定律、断裂力学模型、微观力学模型、随机临界核模型等来计算。除此之外，有限元模拟可以更加准确的预测材料的力学性能，减少实验工作量[7-13]。

目前，对于HFRP的研究多集中于以单向纤维为增强体的复合材料，以平纹织物为增强体的HFRP刚度与强度预测模型以及有限元模拟还很少见。事实上，单向纤维复合材料易于发生纤维间的劈裂，不能实际投入生产应用，平纹织物复合材料才更具优良的力学性能，大量应用于高强度结构制品中[14-17]。

本工作以力学性能优良的碳纤维与玄武岩纤维平纹织物为增强体，制备碳纤维-玄武岩纤维层间混杂增强树脂基复合材料。在ANSYS中，通过计算平纹织物的单胞参数，提供一种较为简便而准确的以平纹织物为增强体的HFRP建模方式。将模型与平纹织物复合材料细观结构模型比较，将其模拟所得值与实验值比较；凭借应力云图明确混杂比对HFRP拉伸时的破坏机制的影响，最终给出HFRP的最优混杂比范围。

1 实验设计

1.1材料

碳纤维平纹织物，吉林丰帆特种纤维有限公司；玄武岩纤维平纹织物，浙江石金玄武岩纤维有限公司；凤凰牌环氧树脂E51，南通星辰合成材料有限公司；2-乙基-4-甲基咪唑，天津市化学试剂厂。碳纤维及玄武岩纤维编织参数见表1。

表1 碳纤维及玄武岩纤维编织参数Table 1 Weaving parameters of carbon fiber and basalt fiber

1.2试件制备与拉伸实验

按照GB/T 3354—2014定向纤维增强聚合物基复合材料拉伸性能试验方法制备9组具有不同混杂比的碳纤维-玄武岩纤维层间混杂增强树脂基复合材料层合板，并且以织物经向为试样长度方向进行切割，每组5件试件，均采用对称嵌层式铺层结构(见表2)。试件采用XLB50X2型平板硫化机热压法成型、WDW-200型电子万能试验机进行拉伸实验。试样沿长度方向拉伸，在试样居中位置安装50 mm标距引伸计，实验加载速率控制为3 mm/min，直至试件断裂。

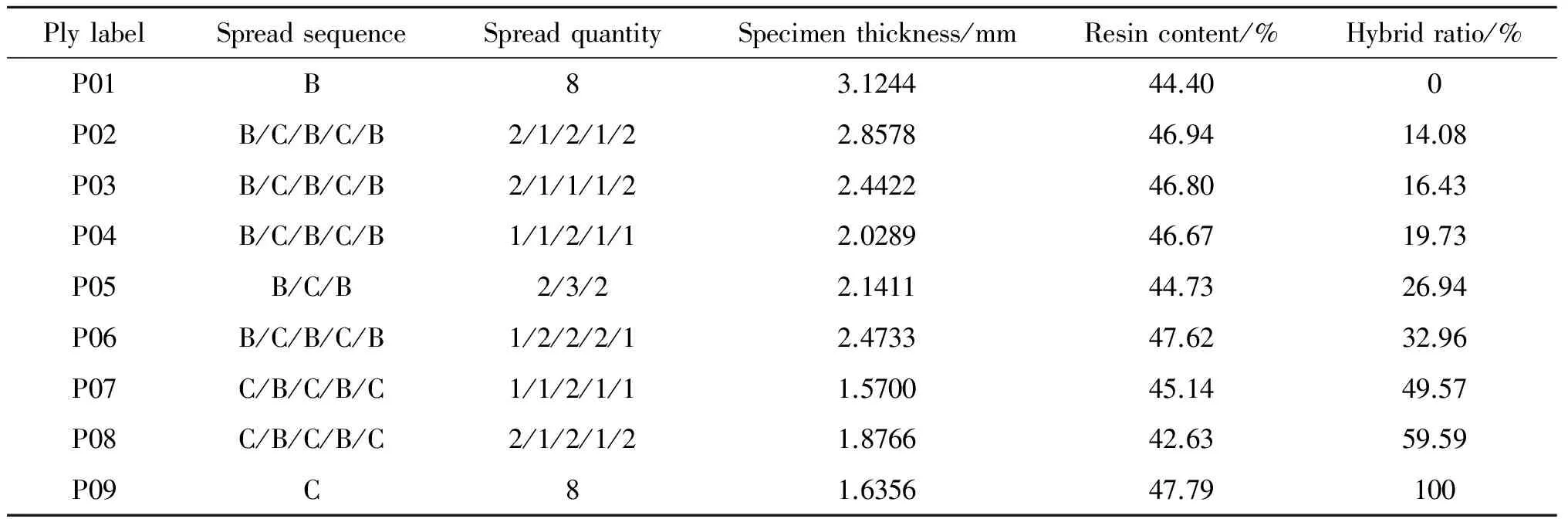
表2 碳纤维-玄武岩纤维混杂增强树脂基复合材料分组Table 2 Groups of carbon/basalt hybrid fiber reinforced resin matrix composites

2 HFRP有限元模型

2.1平纹织物细观结构分析

以往的单向纤维增强复合材料有限元建模方法是以ANSYS中专为复合材料所设计的壳单元体划分实体模型，输入树脂与纤维纱线性能参数并设定层厚、层数以及铺层角度,这显然不适用于平纹织物复合材料。平纹织物包含经、纬两向纱线，在受拉方向上，经向纱线承受主要载荷，纬向纱线起稳固连接作用。

Vandeurzen等[18]提出的纱线轴线为正弦曲线，截面为凸透镜的双凸模型，可以非常直观地表现出平纹织物的细观结构，图1所示为平纹织物的单胞形态。

图1 平纹织物的单胞模型Fig.1 Unit cell of plain weave

如果将一层平纹织物简单化为壳单元体中经、纬两层，并赋予不同性能参数，则会丧失织物原本结构特征，大大降低模拟精准度。因为这种建模方式将原本起稳固连接作用的纬向纤维全部抽离出来，转化为承载部分。纬向纤维力学参数在受拉方向上低于经向纤维两个数量级， HFRP在受拉过程中各部分等位移延伸，这将导致模拟过程中材料过早失效。因此，必须准确计算出平纹织物单胞各方向上的性能参数，将其输入为壳单元体平纹织物层的材料属性，完成有限元建模。

2.2模型建立

根据混合定律，以经、纬纱线不同方向的弹性模量乘以相应体积含量求得平纹织物单胞各方向上的弹性模量：

(1)

式中：表示弹性模量；表示纤维含量，可根据织物编制参数求得；下角标c，b分别表示碳纤维和玄武岩纤维;i,j分别表示平纹织物经向方向与纬向方向；l,t分别表示纤维纱线轴线方向和径向方向。其他性能参数，如剪切模量G、泊松比可以用同样方法求得。

确定平纹织物单胞参数后，创建有限元模型。根据模型中的纤维与实际纤维的体积相等，得到SHELL单元中碳纤维的片层厚度和玄武岩纤维的片层厚度：

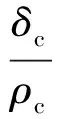
(2)

式中：δ表示织物的面密度；ρ表示纤维的密度。树脂层厚度Hm为：

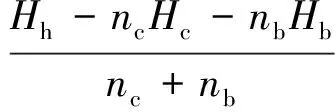
(3)

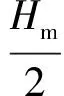
在ANSYS中选定四节点三维壳单元SHELL181定义单元类型，按照上述计算，赋予纤维体正交各向异性属性，树脂为各向同性属性，按表2设置层数与层厚，铺层角为0°。在GUI界面中完成试件实体模型建立并划分网格，至此完成HFRP有限元模型的建立。

2.3模型结构精准度检测

事实上，以壳单元体建立有限元模型仍然简化了平纹织物复合材料的真实结构。目前，有学者提出了单层平纹织物复合材料细观模型的建立方法。但HFRP结构较为复杂，其中包含铺层数目，铺层角度，混杂比例等多个变量。如考虑细观模型建立方法则需建立多层复合材料，为保证正弦曲线结构不至于失真，当中所创建的节点数目之多，将使得计算机运算极为困难，运算周期较长。

通过图1可以看出，平纹织物复合材料是极为扁平的结构，其内部极微小的形状波动对最终模拟结果影响不大。为验证建立的模型对复合材料结构的还原程度，建立了相同尺寸的单层碳纤维平纹织物复合材料的细观结构模型与壳单元体模型，细观结构模型如图2所示。分别固定模型单侧端面，对另一侧端面进行等伸长拉伸，施加位移载荷。通过对节点反力的面内积分，求出受力面的等效拉伸应力。结果显示,细观结构模型等效拉伸应力为123.302 MPa，根据E=δ/ε求得刚度为61.651 GPa。壳单元体模型等效拉伸应力为121.898 MPa，换算为刚度为60.949 GPa。证明本工作建立的模型适用于一般情况下对以平纹织物为增强体的HFRP力学性能的预测。这保证了模拟的精准度，又大大减轻了计算负担。

图2 细观结构模型Fig.2 Model of mesostructure

2.4模型数值精准度检测

为进一步检测本工作所建模型的准确性，将有限元模拟值与实验值进行了比对，对模拟精准度进行检测。按照表2所示信息对试件进行有限元建模，同样方式施加位移载荷。根据E=σ/ε求得复合材料的拉伸刚度。HFRP刚度的实验值与模拟值对比见图3。

图3 碳纤维-玄武岩纤维混杂增强树脂基复合材料弹性模量实验值与模拟值对比Fig.3 Comparison of experimental values and simulated values of elasticity modulus for carbon/basalt hybrid fiber reinforced resin matrix composites

由图3可以看出，实验值与模拟值基本近似，实验所测得数值略小于有限元模拟数值是因为试件制备难以避免孔隙等缺陷。

3 HFRP层合板破坏机制分析

3.1HFRP的强度分析

为确定材料的最优混杂比范围，必须明确材料的破坏机制。实验所测HFRP强度如图4所示，碳纤维含量低于25%左右时，HFRP的抗拉强度随着碳纤维含量的增加而减小，碳纤维含量高于25%左右时，趋势相反。强度值在碳纤维含量为25%左右时出现了最小值，此值被称为临界混杂比。产生此现象的原因是，碳纤维的伸长率小，在HFRP受拉时，其先承受大部分载荷并断裂。这时，若玄武岩纤维含量较多，碳纤维断裂后，其仍具备一定承载能力，HFRP可以继续承载，直至玄武岩纤维失效HFRP才彻底失效。最终HFRP发生二次破坏，强度仅为玄武岩纤维这部分所能承担的极限强度，如式(4)，其中Vc表示混杂比。因此，随着碳纤维含量的增加，HFRP的抗拉强度随之降低。若碳纤维断裂时，玄武岩纤维的含量较少，其不能单独承载，便与碳纤维一起断裂失效，最终HFRP为一次破坏，强度为碳纤维与玄武岩纤维共同承载可经受的极限强度，如式(5)。因此，随着碳纤维含量的增加，HFRP强度也随之增加。

σH=(1-Vc)σb

(4)

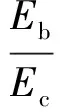
(5)

图4 碳纤维-玄武岩纤维混杂增强树脂基复合材料抗拉强度与混杂比的关系Fig.4 Relationship between tensile strength and hybrid ratio of carbon/basalt hybrid fiber reinforced resin matrix composites

3.2HFRP层合板破坏机制分析

为验证以上结论，基于ANSYS对HFRP进行有限元分析。实际上，以平纹织物为增强体的复合材料中，纤维层的抗拉强度为经向纱线轴向强度与纬向纱线径向强度的叠加，但纱线径向强度要比轴向强度小两个数量级，所以可以忽略纬向纱线的作用。纤维层的抗拉强度可以近似考虑为：

σ≈λi×El

(6)

已知碳纤维纱线抗拉强度为2600 MPa，玄武岩纤维纱线抗拉强度为2200 MPa，根据式(6)可以得到HFRP中碳纤维层和玄武岩纤维层的抗拉强度分别为1266 MPa和905 MPa。

图5显示临界混杂比发生在试样5(混杂比26.94%左右)。实验测得试样5最大可经受335.31 MPa的应力，在其有限元模型上一端施加全约束，一端施加最大应力可得到图5(a)所示的应力云图。可见碳纤维所受应力刚好达到其抗拉强度，将碳纤维层退化，使其作用与树脂一样，可以得到如图5(b)的应力云图，此时玄武岩纤维所受应力也超过了其抗拉强度。可见在碳纤维破坏之后玄武岩纤维也无法继续承载，HFRP发生一次断裂。

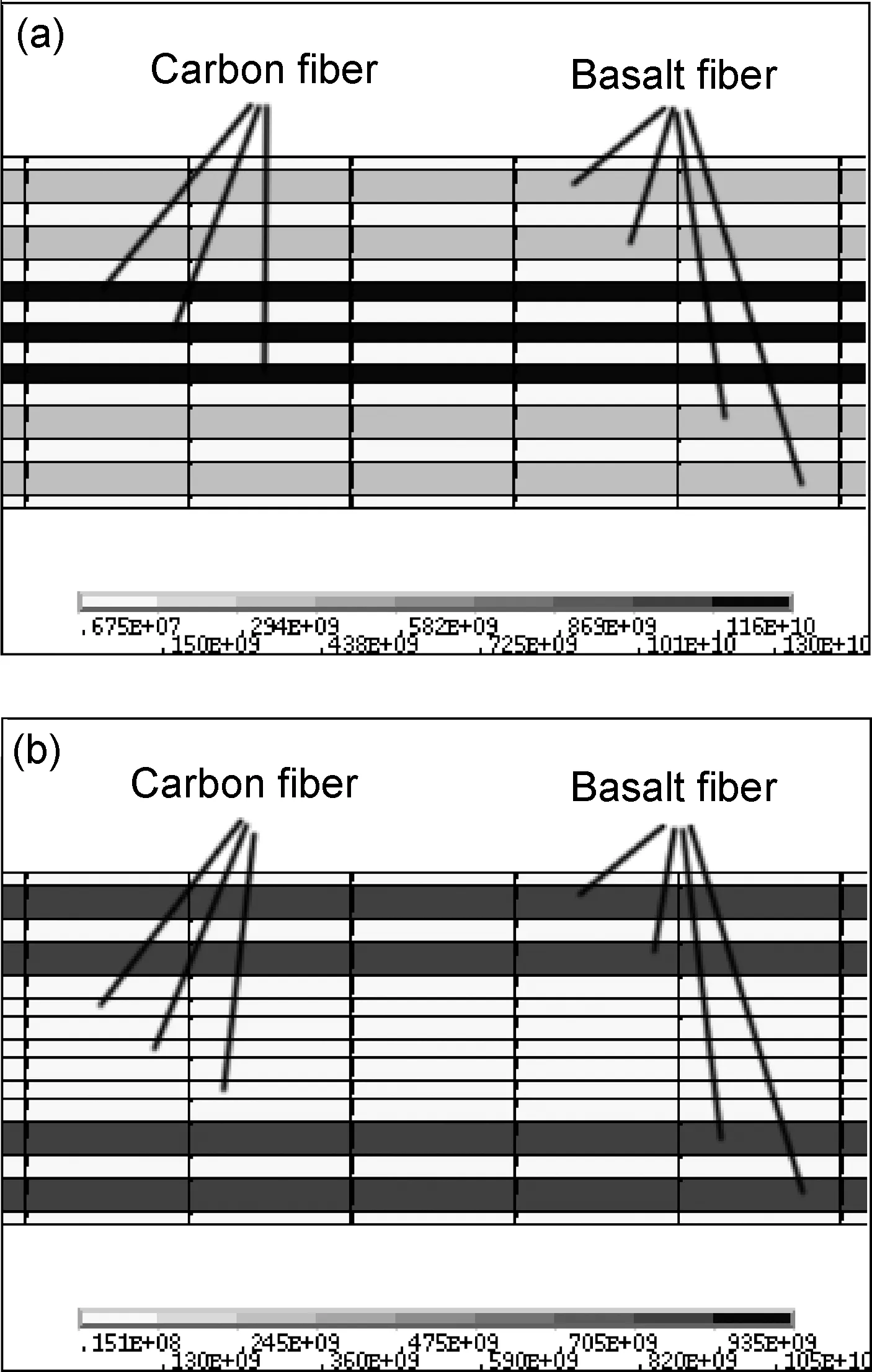
图5 试样5应力云图 (a)碳纤维未失效；(b)碳纤维失效Fig.5 Stress nephogram of P05 (a)carbon fiber does not lose efficacy;(b) carbon fiber loses efficacy

再来考察试样4(见图6)。实验测得试样4最大可经受387.19 MPa的应力。对其加载可以得到图6(a)所示的应力云图。可见碳纤维层的应力已达到1280 MPa，超过了抗拉极限，此时碳纤维应已失效，将碳纤维层退化可以得到如图6(b)所示的应力云图，此时玄武岩层所受应力刚好达到抗拉强度。显然，试样4断裂时是碳纤维先发生断裂，载荷继续由玄武岩纤维承担，最终HFRP发生二次破坏。

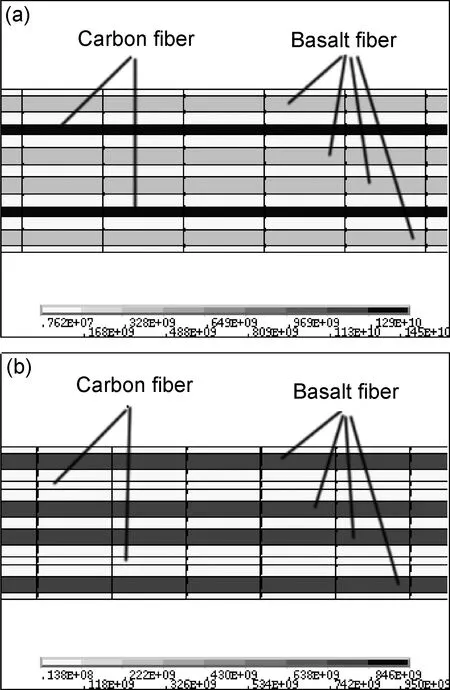
图6 试样4应力云图 (a)碳纤维未失效;(b)碳纤维失效Fig.6 Stress nephogram of P04 (a)carbon fiber does not lose efficacy;(b)carbon fiber loses efficacy

4 混杂比的优化设计

根据以上分析，确实存在一个临界混杂比值，HFRP的强度与极限拉伸应变必将会在此值处存在转折点。此临界混杂比区分HFRP层合板发生一次破坏还是二次破坏。二次破坏是实际应用中不被允许的，最优混杂比范围不得将其包含其中。

ANSYS模拟可以排除孔隙率，制备工艺，树脂含量不同等影响因素所带来的实验误差，在理论上给出准确结论。因此，模拟得出HFRP的刚度、强度、拉伸极限应变与混杂比的关系曲线。模拟时将树脂含量定为45%。

按2.3节所述即可对刚度进行模拟。强度模拟则按照Hashin破坏准则通过UPFs自行编译,用户自定义失效准则。在ANSYS中不断对HFRP增加应力载荷直至纤维层全部失效，即输出强度模拟结果，同时可获得材料的拉伸极限应变。最终模拟曲线见图7。

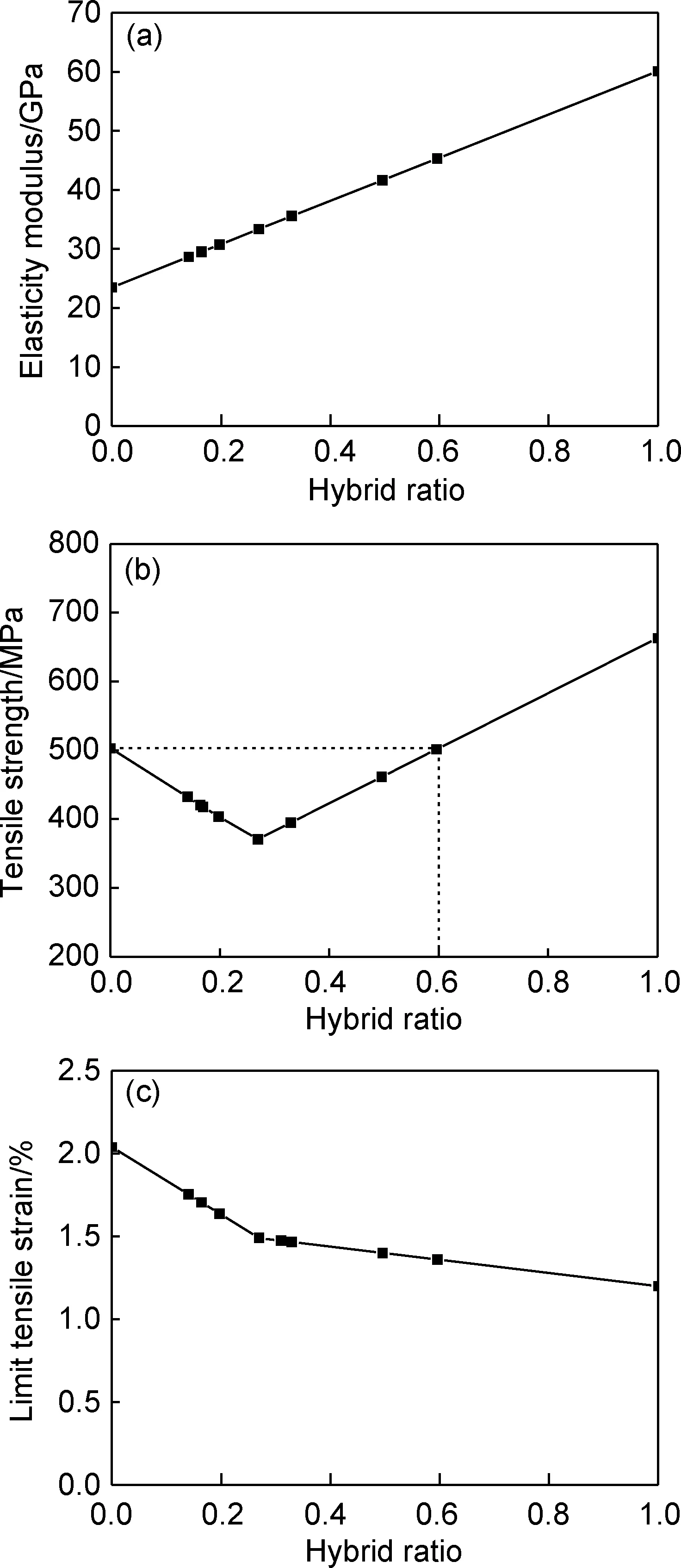
图7 碳纤维与玄武岩纤维混杂增强树脂基复合材料树脂含量为45%时力学性能模拟曲线 (a)弹性模量与混杂比的关系；(b)抗拉强度与混杂比的关系；(c)拉伸极限应变与混杂比的关系Fig.7 Simulation curve of mechanical property for carbon/basalt hybrid fiber reinforced resin matrix composites with 45% resin content (a) relationship between elasticity modulus and hybrid ratio；(b)relationship between tensile strength and hybrid ratio；(c)relationship between limit tensile strain and hybrid ratio

由图7可见，在排除HFRP发生二次破坏范围(0%

5 结 论

(1)对以平纹织物为增强体的HFRP的有限元建模方式可以准确预测HFRP的各项性能。碳纤维与玄武岩纤维混杂增强树脂基复合材料刚度随混杂比(碳纤维含量)增加而增加，符合混合定律；强度在混杂比为25%左右时出现最小值，这种现象与HFRP破坏机制有关。提供的ANSYS分析方法可以验证不同混杂比对HFRP的破坏机制的影响。

(2)当混杂比大于60%且不等于100%时，可保证HFRP强度、刚度、拉伸极限应变均有提高。当混杂比为60%时可保证HFRP强度无折减的情况下，刚度较玄武岩纤维复合材料提高93.4%，拉伸极限应变较碳纤维复合材料提高11.3%。

[1] VALENZA A，FIORE V，DI BELLA G．Effect of UD carbon on the specific mechanical properties of glass mat composites for marine applications[J]．Journal of Composite Materials，2010，44(11)：1350-1364．

[2] SUN X S，CHEN Y，TAN V B C，etal．Homogenization and stress analysis of mutilayered composite offshore production risers[J]．Journal of Applied Mechanics，2014，81(3)：1-11．

[3] KOTHA S P，CUZELSU N．Tensile behavior of corti-cal bone：dependence of organic matrix material properties on bone mineral content[J]．Journal of Biomechanics，2007，40(1)：35-45．

[4] HAYASHI T．On the improvement of mechanical properties of composites by hybrid composition [C]∥ Proceedings of the 8th International Reinforced Plastics Conference.Brighten,UK:[s.n.],1972．

[5] ZHANG Y，LI Y，MA H，etal．Tensile and interfacial properties of unidirectional flax/glass fiber reinforced hybrid composites[J]．Composites Science and Technology，2013，88(14)：172-177．

[6] 张普，朱虹，孟少平，等．CFRP/BFRP混杂效应试验研究和理论分析[J]．工业建筑，2011，41(3)：103-107．

(ZHANG P，ZHU H，MENG S P，etal．Theoretical analysis and test research on hybrid effect of CFRP/BFRP hybrid fiber[J]．Industrial Construction，2011，41(3)：103-107．)

[7] SWOLFS Y，GORBATIKH L，VERPOEST I．Fiber hybridisation in polymer composites：a review[J]．Composites Part A：Applied Science and Manufacturing，2014，67(12)：181-200．

[8] 张小东，王耀杰，邓宗才．混杂纤维片材拉伸性能研究[J]．国防交通工程与技术，2010，8(1)：21-25. (ZHANG X D，WANG Y J，DENG Z C．An experimental study of the tensile properties of IHFRP[J]．Traffic Engineering and Technology for National Defence，2010，8(1)：21-25．)

[9] 范赋群，曾庆敦，黄小清．复合材料的统计断裂理论[J]．力学与实践，2000,22(2)：1-5．

(FAN F Q，ZENG Q D，HUANG X Q．Probabilistic fracture theories for composites[J]．Mechanics in Engineering，2000，22(2)：1-5．)

[10] 李卫东，曹海琳，魏斌，等．BF/CF层间混杂结构对复合材料性能影响[J]．热固性树脂，2009，24(5)：39-43.

(LI W D，CAO H L，WEI B，etal．Effect of CF/BF interlaminated hybrid structure on composite properties[J]．Thermosetting Resin，2009，24(5)：39-43．)

[11] QU P，GUAN X J．JIA Y X，etal．Effective elastic properties and stress distribution of 2D biaxial nonorthogonally braided composites[J]．Journal of Composite Materials，2012，46(8)：997-1008．

[12] AYRANCI C and CAREY J P．Predicting the longitudenal elastic modulus of braided tubular composites using a curbed unit-cell geometry[J]．Composites Part B：Engineering，2010，41(3)：229-235．

[13] NASU S，OHTANI A，NAKAI A，etal．Deformation behavior and mechanical properties of braided rectangular pipes[J]．Composite Structures 2010：92(3)：752-756．

[14] PAPANICOLAOU G C，MOUZAKIS D E，KOSMIDOU T V．Static and dynamic behavior of single-edge notched glass fabric composites[J]．Polymer Composites．2006．27(2)：177-183．

[15] 魏广恒．基于变分原理的机织复合材料细观力学模型[D]．天津：天津工业大学，2006．

(WEI G H．The micro-mechanics model of the woven fabric composite based on variational principle[D]．Tianjin：Tianjin Ploytechnic University，2006．)

[16] SHROTRIYA P，SOTTOS N R．Viscoelastic response of woven composite substrates[J]．Composites Science and Technology，2005，65(3/4)：621-634．

[17] 左中鹅，王瑞，徐磊．基于有限单元法的平纹织物复合材料强度预测：1．RVE的有限元模型[J]．纺织学报，2009，30(12)：45-49．

(ZUO Z E，WANG R，XU L．Mechanical strength prediction of plain woven fabric composite 1．finite element model of composite RVE[J]．Journal of Textile Research，2009，30(12)：45-49．)

[18] VANDEURZEN P，IVENS J，VERPOEST I．Structure performance analysis of two-dimensional woven fabric composites[J]．Polymers & Polymer Composites，1996，4(5)：361-367．

(责任编辑：徐永祥)

OptimalDesignforHybridRatioofCarbon/BasaltHybridFiberReinforcedResinMatrixComposites

XU Hong， LU Yan， ZHANG Ke， LIU Shuan， WANG Xianghui， DOU Yanli

(School of Materials Science and Engineering, Jilin University, Changchun 130025, China)

The optimum hybrid ratio range of carbon/basalt hybrid fiber reinforced resin composites was studied. Hybrid fiber composites with nine different hybrid ratios were prepared before tensile test.According to the structural features of plain weave, the unit cell’s performance parameters were calculated. Finite element model was established by using SHELL181 in ANSYS. The simulated values of the sample stiffness in the model were approximately similar to the experimental ones. The stress nephogram shows that there is a critical hybrid ratio which divides the failure mechanism of HFRP into single failure state and multiple failure state. The tensile modulus, strength and limit tensile strain of HFRP with 45% resin are simulated by finite element method. The result shows that the tensile modulus of HFRP with 60% hybrid ratio increases by 93.4% compared with basalt fiber composites (BFRP), and the limit tensile strain increases by 11.3% compared with carbon fiber composites(CFRP).

hybrid fiber composites； carbon fiber； basalt fiber；plain weave； hybrid ratio

2017-04-10；

2017-05-24

吉林省“双十”重大科技成果转化项目(3D515AI92416)；吉林大学大学生创新创业训练计划(2016A43127)

窦艳丽(1979—)，女，博士，副教授，研究方向为混杂纤维制备与性能，(E-mail)douyl@jlu.edu.cn。

10.11868/j.issn.1005-5053.2017.000047

TB332

： A

： 1005-5053(2017)04-0007-07