一个具有Logistic增长和CTL免疫反应的乙肝病毒感染模型

陈志伟 代安华

重庆轻工职业学院

一个具有Logistic增长和CTL免疫反应的乙肝病毒感染模型

陈志伟 代安华

重庆轻工职业学院

本文建立了一个考虑Logistic增长和CTL免疫反应的乙肝病毒感染模型. 模型有三个平衡点. 由 Routh-Hurwitz判据分别得到无感染平衡点，无免疫平衡点和正平衡点的局部渐近稳定性. 用数学分析以及比较原理证明无病平衡点的全局渐近稳定性。

Logistic增长 CTL免疫反应 稳定性

1996年，Nowak等[1]借鉴仓室模型的建模思想提出一个三维乙肝病毒感染模型：

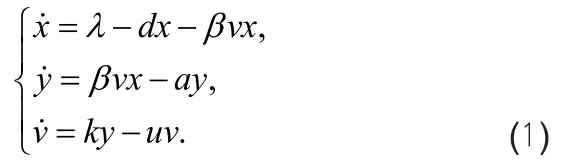
2008年，闵乐泉等[2]将标准发生率代替简单质量作用律发生率：

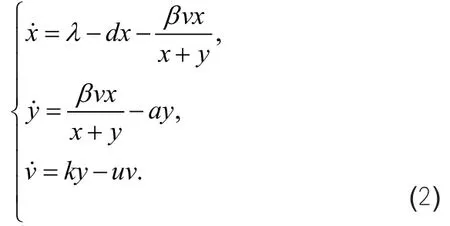
2010年，Hews等[3]假设未感染细胞繁殖遵循Logistic 生长规律，建立了带标准发生率的乙肝病毒感染模型：

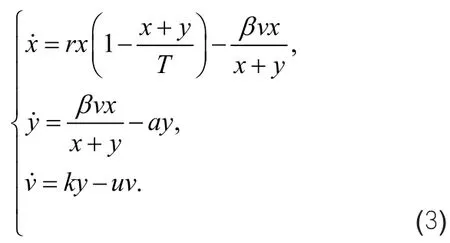
本文在文献[3]基础上加入CTL免疫反应，建立以下乙肝病毒感染模型：

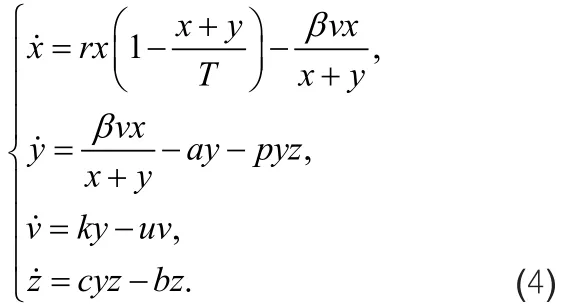
其中：x 是未感染细胞数量，y是感染细胞的数量，v 是自由病毒数量，表示免疫细胞的数量，T 是指细胞的最大承载量，是未感染细胞的内禀增长率，是标准发生率，ay 是感染细胞的死亡速率，ky是病毒的产生速率，uv 是病毒的死亡速率，pyz 表示免疫机制引起的感染细胞的死亡率，cyz 是免疫细胞产生速率，bz是免疫细胞的死亡率。

一、平衡点和基本再生数

系统(4)总是存在一个无感染平衡点：

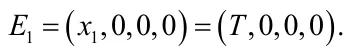
系统(4)的病毒基本再生数定义为：

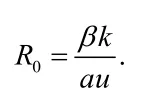
定义两个新的阈值：

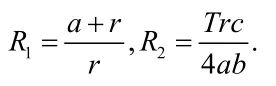
当R1＞R0＞1时，存在一个无免疫平衡点:

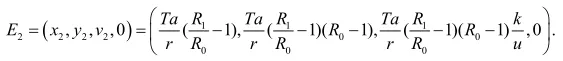
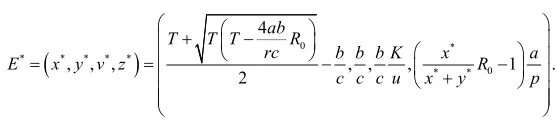
二、稳定性分析

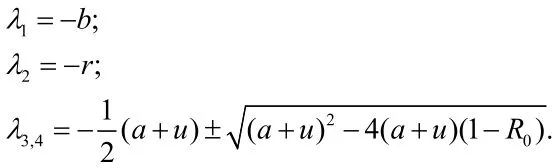
证明 由系统(4)易知

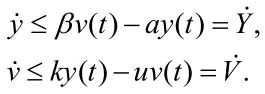
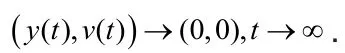
定理3 令

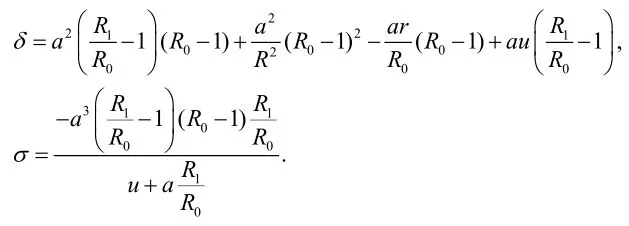
三、结论

本文研究了一个具有Logistic增长项和CTL免疫反应的乙肝病毒感染模型. 模型有三个平衡点：无感染平衡点，无免疫平衡点和正平衡点. 根据Routh-Hurwitz判据得到了三个平衡点的局部稳定性的条件. 根据比较原理得到了无感染平衡点的全局渐近稳定性. 免疫反应分两类，除了CTL免疫还有抗体免疫，因此可以在系统(4)上再加一项进行研究，这将是我们今后的工作.

[1] Nowak M A, Bonhoeffer S, Hill A M,et al. Viral dynamics in hepatitis B virus infection[J]. Proceedings of the National Academy of Science of the Uinited States of America, 1996, 93: 4398-4402.

[2]Min L Q, Su Y M, Kuang Y.Mathematical analysis of a basic virus infection model with application to HBV infection[J]. Rocky Mountain Journal of Mathematics, 2008, 38(5): 1573-1585.

[3] Hews S, Eikenberry S, Nagy J D, et al. Rich dynamics of a hepatitis B viral infection model with logistic hepatocyte growth [J]. Journal of Mathematical Biology, 2010, 60(4): 573-590.