输电导线建模方法及舞动研究

芮静敏，刘丽红，姚佳

（北京电子科技职业学院汽车工程学院，北京100176）

输电导线建模方法及舞动研究

芮静敏，刘丽红，姚佳

（北京电子科技职业学院汽车工程学院，北京100176）

架空输电导线的舞动给输电线路安全造成了重大威胁。在对导线舞动的模拟研究中，目前，常采用的有限元建模方法不能很好地进行导线舞动的动力学分析。因此，结合有限元化和ADAMS柔性理论建立输电导线的柔性体模型，对输电导线进行舞动模拟，更加方便和精确地得到了导线舞动过程中动力学特性以及两端塔杆的受力情况，为输电导线类大型柔性体的动力学模拟提供了依据，同时，为输电导线防舞动研究提供了新思路。

导线模型；柔性体；动力学特性；大跨越线路

架空输电线路在冻雨、雨凇或大风天气时，导线表面覆冰易形成非圆横截面，在一定的条件下，会诱发输电线产生低频率（0.1～3 Hz）、大振幅（可达10 m以上）的舞动（Dancing）。舞动振幅通常较大，导致引起相间闪络、跳闸、金具损坏甚至断线倒塔，成为输电线路尤其是超高压、大跨越线路的重大灾害之一。因此，深入开展导线舞动研究，对保证我国输电线路安全意义重大。

在对导线舞动的模拟研究中，输电导线模型的建立至关重要。然而，目前的模拟研究通常采用流体计算类软件，比如FLUENT等进行，基于输电塔线体系静动力特性，通常采用整体有限元的方法。其中，导线通常采用简化的模型，比如采用LINK10杆单元，特有的双线性刚度矩阵特性可以模拟轴向仅受拉或仅受压的情况，但是该单元不包括弯曲刚度，且模拟钢缆静态的效果较好。

输电导线的舞动属于导线的变形，是相对于物体坐标系的弹性小变形，同时，物体坐标系又经历了大的非线性整体移动和转动，与ADAMS中柔性体属性相符合。有限元分析软件对包含大位移运动的系统动力学分析无能为力，因此，本文运用ADAMS柔性理论建立输电导线柔性体模型，进行导线舞动模拟研究，相比将输电塔线体系整体有限元化，以及直接在ADAMS中直接生成柔性体（刚体铰接）的方法，可以更加方便和精确地研究导线舞动过程中动力学特性以及舞动过程中两端塔杆的受力情况。

1 输电导线模型的建立

根据邓哈托垂直舞动机理，不考虑横向运动以及自身扭转，单根导线的舞动可简化为正弦运动，设初始位置为0，运动方程式可表示为：

式（1）中：A为导线振动振幅；ω为其振动频率。

ADAMS可以与大多数主流有限元软件ANSYS、NASTRAN、ABAQUS接口，通过有限元软件生成表示物体柔性体模型的模态中性文件（MNF），再通过接口将该柔性体模型导入ADAMS/View或ADAMS/Solver中。流程如图1所示。

在ADAMS中导入模态中性文件后，柔性体会被放在整体惯性坐标系的原点上，与模型中其他部分没有任何关系。

图1 生成模态中性文件流程图

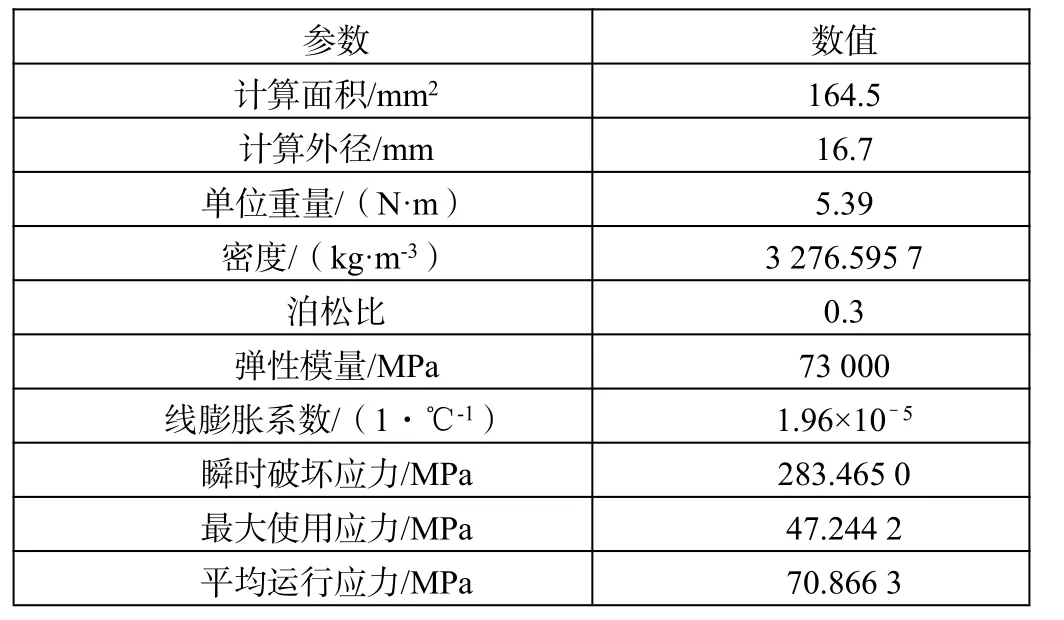
表1 导线结构特性参数

需要在柔性体与其他刚体或柔性体之间建立运动副约束关系，还需要在柔性体上施加载荷等。如果直接在柔性体与刚形体之间建立连接关系，由于理论等条件的限制，很多连接无法建立。比如，柔性体与刚形体之间不能建立柔性连接，当柔性体是施力物体时才能在其上施加具有6个分量的广义力向量、具有3个分量的力向量、具有3个分量的力矩向量等。如果柔性体是被加载物体，不能在柔性体上施加多分量力和力矩，不能施加滑移副约束和平面副约束等。此时，可以通过建立一种虚构件（Dummy Part）去掉物体的几何体或将构件的质量和惯性矩等质量信息设置为0，并通过虚构件建立柔性体与其他件之间的连接。

在ADAMS中对LGJ-150/20导线建模，导线结构特性参数如表1所示。

输电导线两端悬挂点间距往往较长，其刚性对悬挂时的几何外形影响很小，通常将其假定为1根各个节点铰接的链条。另外，假设导线作用的荷载均指向同一方向并且沿着导线长度均匀分布。以上假定即为导线悬挂后呈现“悬链线”状态的最基本假定。因此，根据悬链线法计算出导线的垂度和导线上各点的坐标值，两个悬挂点不等高或高差系数较大时，常采用斜抛物线方程；两个悬挂点等高或者高差系数较小时，常采用平抛物线方程。导线的斜抛物线方程为：

档距中央的最大弧垂为：

导线任意一点的弧垂为：

式（2）（3）（4）中：h为两悬挂点的高差，即两悬挂点间在比载作用方向的比值；β为导线悬挂点的悬高差；σ0为初始应力，即单位截面积作用张力；γ为比载，即导线单位长度单位截面所承受的载荷；l为垂直于比载作用方向的投影距离。

建立100 m等高档距导线模型，所建立单档距的输电导线模型均为两端等高悬挂，以导线中点所在的竖直方向直线对称舞动。其中，点弧垂如表2所示。导线模型如图2所示。其中，采用旋转副模拟导线与输电杆塔的连接。

表2 导线弧垂

2 输电导线舞动模拟

输电导线舞动是一种复杂的流固耦合振动，其舞动成因复杂，现有模拟软件不能完全从舞动机理上再现舞动的真实情况。本文对输电导线的舞动模拟不从舞动机理上进行，而是从其舞动本质-受力角度出发。以导线中点为测量点，测得的舞动振幅表示舞动状态。

进行稳定舞动模拟，测得导线中点Y方向、X方向和Z方向位移曲线如图3、图4、图5所示。

图2 等高档距输电导线模型

图3 100 m档距导线稳定舞动时中点Y方向位移时程图

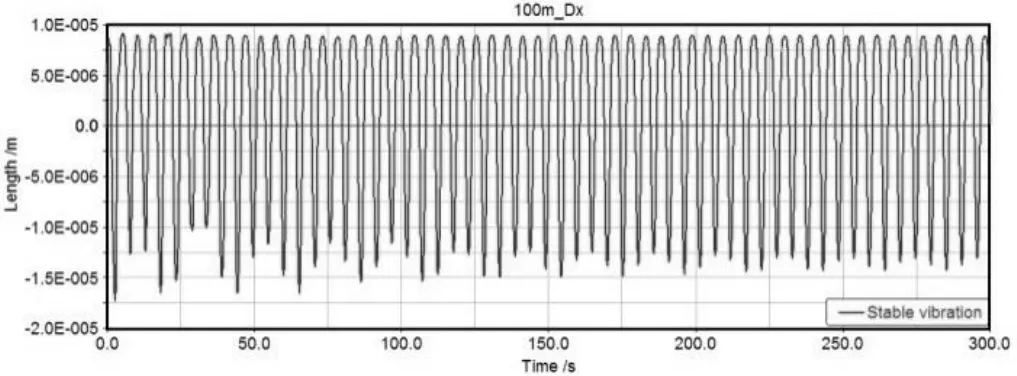
图4 100 m档距导线稳定舞动时中点X方向位移时程图

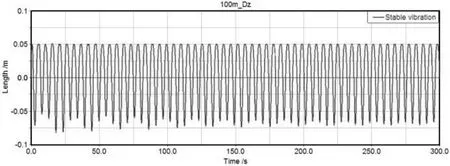
图5 100 m档距导线稳定舞动时中点Z方向位移时程图

测量杆塔X方向、Y方向受力曲线如图6、图7所示。从图3、图4、图5中可以看出，输电导线稳定舞动时，X方向和Z方向舞动振幅极小，可以忽略，仅考虑垂直舞动。Y方向舞动振幅均值为9.62 m，振幅幅值9.96 m，舞动周期为5.2 s，频率为0.19 Hz，符合频率0.1～3 Hz的低频舞动。

图6 100 m档距导线稳定舞动时杆塔X方向受力时程图

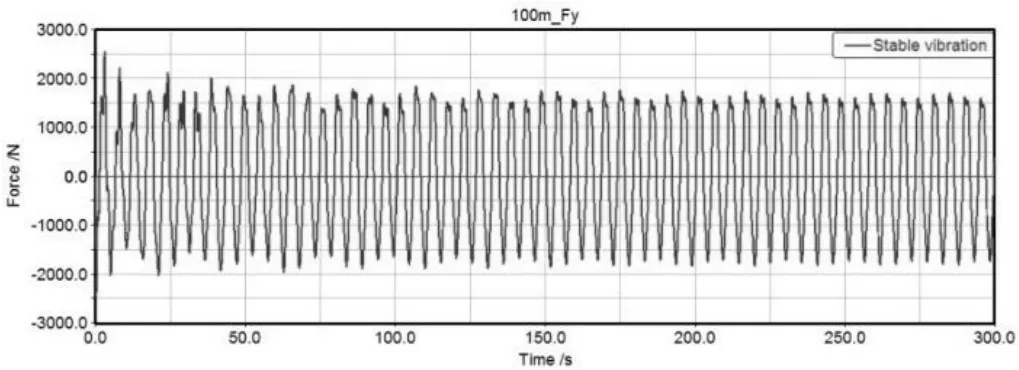
图7 100 m档距导线稳定舞动时杆塔Y方向受力时程图

3 结束语

本文基于邓哈托垂直舞动机理，不考虑导线横向运动以及自身扭转，建立了单根导线舞动的数学模型，运用ADAMS柔性理论建立100 m等高档距导线柔性体模型，成功地进行了导线稳定舞动过程的模拟，测得导线中点X方向、Y方向和Z方向位移，并测得了导线两端杆塔在X方向、Y方向的受力情况。为输电导线类大型柔性体的动力学模拟提供了成功的范例，同时为输电导线防舞动的研究提供了新思路。

〔编辑：张思楠〕

TM75

：A

10.15913/j.cnki.kjycx.2017.15.003

2095-6835（2017）15-0003-03

芮静敏（1988—），女，硕士，毕业于北京理工大学，主要研究安全技术。