电动汽车无刷直流电机能量回馈制动系统设计

赵景波, 王代超, 李 卉, 师 琦

(青岛理工大学 自动化工程学院，山东 青岛 266520)

电动汽车无刷直流电机能量回馈制动系统设计

赵景波, 王代超, 李 卉, 师 琦

(青岛理工大学 自动化工程学院，山东 青岛 266520)

就电动汽车能量回馈制动效率较低的问题提出了一种恒转矩模糊控制策略。首先分析了无刷直流电机能量回馈制动的基本原理，对不同的回馈控制策略进行了对比分析，设计了一个三维模糊控制器，再以该控制器为核心，在MATLAB/Simulink环境中搭建了无刷直流电机能量回馈制动系统的仿真模型，并进行仿真。仿真结果显示提出的控制策略对电机制动转矩以及能量回收达到了很好的控制效果。

汽刷直流电机； 能量回馈; 恒转矩; 三维模糊控制器; 电动汽车

0 引 言

目前，世界各国政府都制定了利于本国电动汽车中长期发展的战略规划。关于电动汽车能量回馈制动方面，国内外的企业和学者做了各种研究，如清华大学联合北京客车总厂等单位研制的燃料电池城市客车，采用燃料电池与动力电池的混合驱动型式，运行考核总里程超过10 000 km；在国外，日本东京R&D公司在电动汽车上使用超级电容实现回馈制动，可将电动汽车行驶里程提高20 km，动力电池的使用寿命也延长1.5倍。但是，在整车技术上，国外研制的电动汽车持续里程比我国大，而且在电动车关键技术蓄电池方面，国外也较国内技术成熟[1-2]。

文献[3-4]介绍了无刷直流电机的工作原理和数学模型;文献[5]提出了一种新型可变电压系统作为电动汽车驱动系统;文献[6-10]介绍了几种常用的控制策略;文献[11]介绍了防抱死技术与能量再生制动的结合，但是该文并未对此作出深入研究；文献[12-14]讲述了能量回馈制动的仿真研究。

本文提出了一种恒转矩模糊控制策略来对电机的能量回馈制动进行控制，设计了一个三维模糊控制器，并以模糊控制器为控制核心，在MATLAB环境中搭建了无刷直流电机能量回馈制动系统的仿真模型，进行了仿真试验，对仿真结果进行了全面分析。

1 能量回馈制动的工作原理

无刷直流电机能量回馈制动的工作原理是指当电动汽车发生制动时，通过控制驱动器中各个电子开关的通断，使电机由电动状态转换到发电状态，从而可以达到向蓄电池反向充电的目的。

能量回馈制动系统主要由蓄电池、电机及控制器三部分组成。图1所示为无刷直流电机驱动电路的原理图[3-4]。

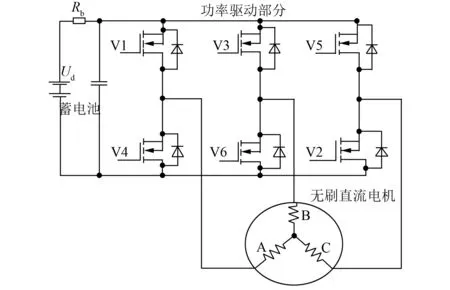
图1 无刷直流电机驱动电路图

在汽车制动的过程中要实现向电池回馈能量而不是向蓄电池中吸取能量的目的，在此可以通过升压斩波的控制方式来实现能量回馈制动。其电路图以及工作波形图分别如图2和图3所示。

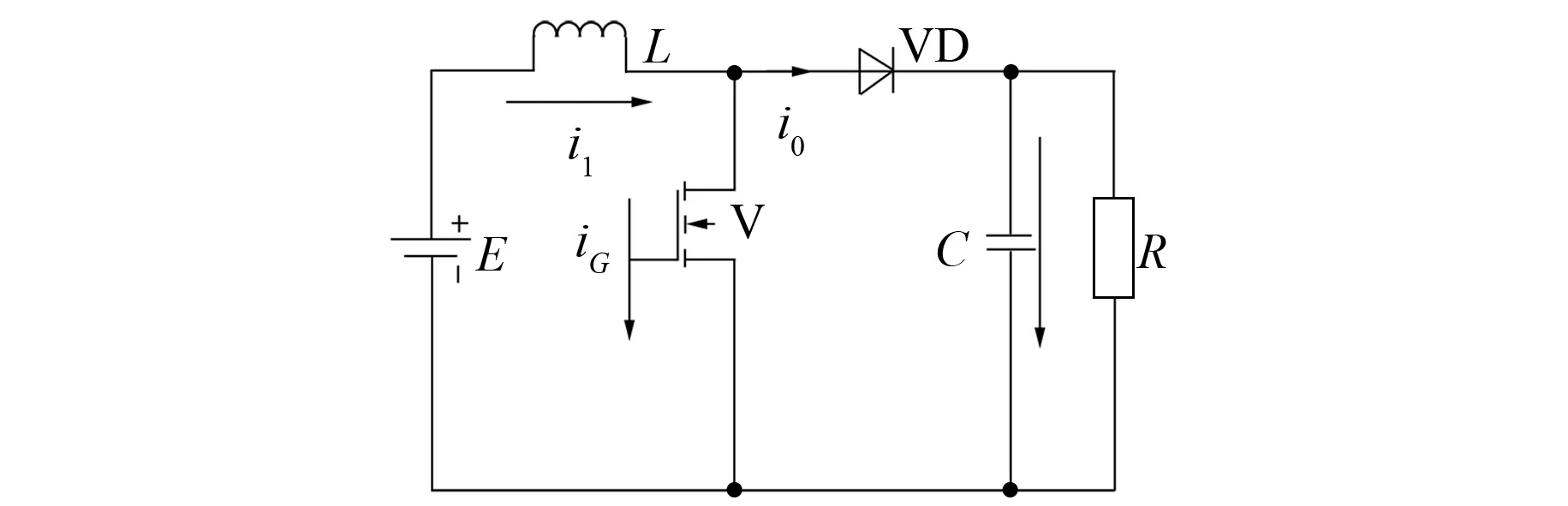
图2 升压斩波电路图

图3 升压斩波电路工作波形图

假设电机中的电感L和电容C都足够大，当功率管V导通时，蓄电池E向电感充电，此时的供电电流为I1。同时电机中的电容向电阻供电，并且由于电容很大，所以电容电压不发生变化，恒为U0。假设功率管开通的时间为ton,则此时蓄电池向电感中充电的能量值为

当功率管关断时，此时蓄电池和电感同时向电容充电并向电阻供电，假设功率管关断的时间为toff，则此时间段内电感释放的能量值为

在稳态状态下，一个周期内电感充电过程中收集的能量和放电过程中释放的能量大小相同,即：

可得

脉宽调制(Pulse Width Modulation,PWM)是通过功率管的开关作用，将恒定的直流电压转换为宽度可调的方波脉冲电压。通过调节脉冲电压的宽度即占空比α，控制输出电压的平均值，是一种基本的电机控制技术。

当电机正向旋转时，在一个周期内，通过对驱动器内的不同功率管进行斩波，就可以生成升压斩波回路，形成制动性质的电机转矩，并向电池充电。在一个周期内，能量回馈过程分为两个阶段，如图4所示。在t1～t2阶段，绕组电感从磁场中获得磁场能量，此时绕组电流变大，这个过程称为续流状态；在t2～t3时间段内，绕组电感中的感应电动势与电路中的反电动势共同向蓄电池充电，导致回路中的电流变小，这个状态称为充电状态[5-6]。

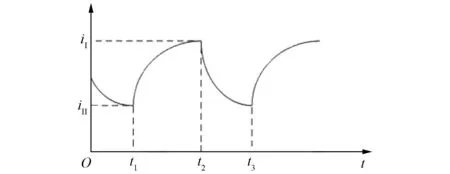
图4 能量回馈制动过程中的电流波形图

2 能量回馈制动的数学模型

2. 1 能量回馈制动的数学模型

当电机转速较快时，系统具有较大的反电动势，此时系统的电枢电流为连续的状态，如图5所示。随着制动过程的进行，电机转速逐渐降低，此时反电动势也逐渐变小；当电机转速下降到某一较低状态时，此时可能导致在一段时间内电机内部无电流通过，电机处于一个断续的工作状态。其电枢电流波形图如图6所示。下面就这两种状态来建立电机回馈制动过程时的数学模型。

图5 能量回馈制动时电机电枢电流连续工作状态时的波形图

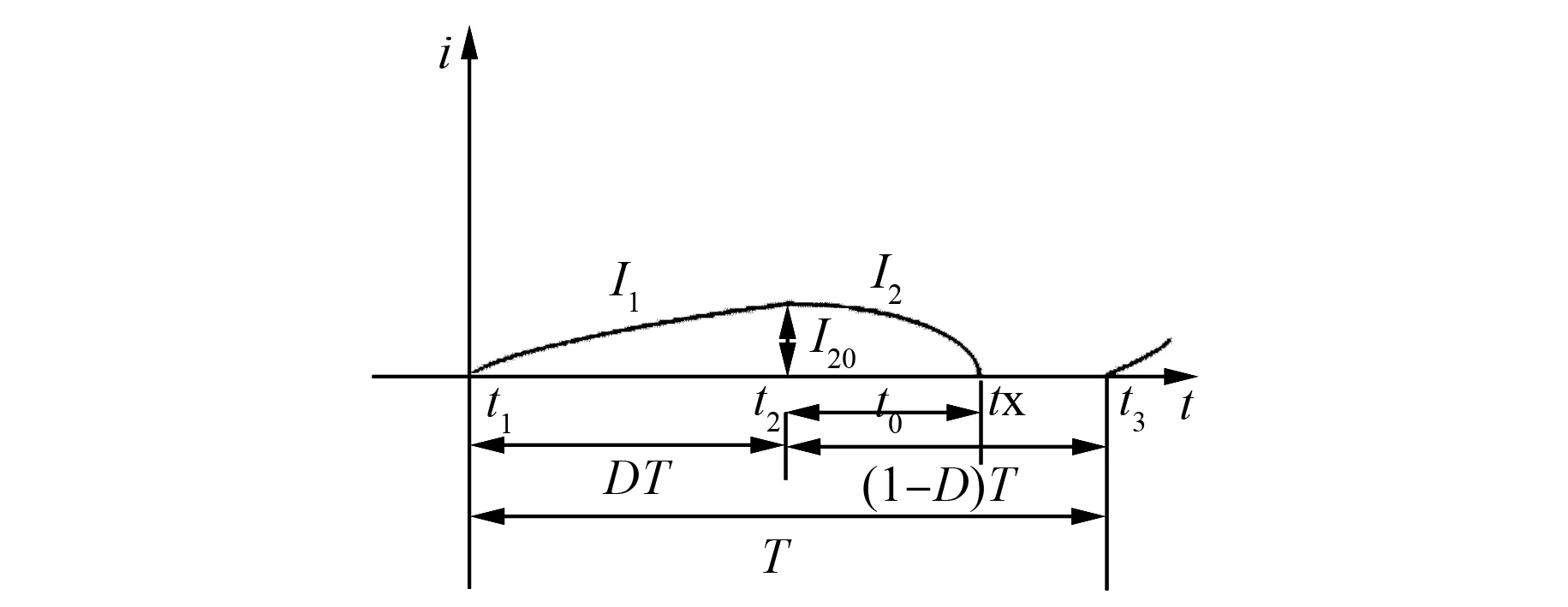
图6 回馈制动时电机电枢电流断续工作状态时的波形图

当电机的电枢电流处于连续的工作状态时，由图5可知其此时电流的数学表达式为

可以求出其上升阶段的电流为

其中:τ=L/R

式中：E——系统的反电动势；R、L——系统的电阻和电感；I1——电流上升阶段的实时电流值；C1——积分常数。

当时间t=t1=0时，此时续流状态电流上升阶段I1的初始值为I10，则可以得出电流上升阶段电流I1的方程表达式为

同理根据图5可以求出电流下降阶段电流I2的方程表达式为

可得出：

式中:Ub——电池的端电压；I2——电流下降阶段的实时电流;C2——积分常数。

令t=t1=0,I20为电流下降阶段的初始值，同时I20也是电流上升阶段的最大值，即电流上升阶段t=t3=(1-D)T时的值，根据式(8)可求得I20。

进而求得在t2～t3时间段内电流下降阶段的方程表达式为

当t=t3=(1-D)T时，此时I2=I10,进而可得

在电流下降阶段，当I10=0时，根据式(13)可以知道，当电流由连续状态到断续状态时所需占空比的临界值。

可以求出电机在连续状态下的能量回馈制动的效率：

电机的电枢电流处于断续的工作状态时，由图6可知其此时电流的数学表达式。其推理过程与连续工作状态时类似。

当电流处于上升阶段时，即t=t1=0，此时I1=0，可得到电流上升阶段的表达式为

得到电流下降阶段的表达式为

当I2=0，可以求得在一个PWM周期内，整个能量回馈制动系统向蓄电池回馈电流的时间：

可以求出电机在断续状态下的能量回馈制动的效率：

当电机电枢电流在连续状态时，假设此时电机电枢电流平均值为I，根据在一个脉冲周期内电机电流上升阶段的上升量等于其下降阶段的下降量原则，可以得到式(20)。其中当电机电流处于断续状态的时间段时，看作电机的电枢电流和回馈电流均为0。

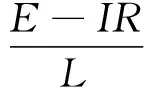
进而得到电流：

其中：α=(1-D)T

式中:r——电池内阻。

在能量回馈制动的过程中，要保证系统向蓄电池充电，就要保证电流I>0，代入式(21)，可得到要进行能量回馈制动时PWM占空比需要满足的要求为

此时在一个PWM周期内回馈电流的平均值为

从而求得回馈制动的功率:

能量回馈制动效率可表示为

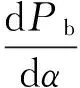
进而可求得能量回馈制动过程中理想模型下的最大回馈电流和最大回馈功率：

2. 2 能量回馈制动的控制策略

当电机转速减小时，控制器检测到减速信号，进而控制PWM波进行能量回馈制动。只有当电机转速、电池荷电状态、制动系统状态都满足特定要求后，才可以进行能量的回馈制动。

根据控制目标的不同，可以把能量回馈制动控制策略分为最大回馈功率控制策略、恒值制动电流的控制策略、最大制动电流控制策略及最大回馈效率制动控制策略。

恒值制动电流控制模式的控制方式是制动电流根据指令的变化来调节制动力矩的大小。由式(21)可知，当占空比发生变化时，要使制动电流保持不变，则就要使电路中回馈电流的最大值等于制动电流，可得出此时的占空比为零。当占空比为1时，回馈电流则为0。电池的承受能力有限，其充电电流不能超过其最大允许充电电流，因此设置最大制动电流等于电池允许的最大充电电流，而这样会导致能量的回收效率降低[7]。

最大回馈效率控制回馈效率高，回馈的能量多，但其必须要考虑到负载阻力矩。在实际的应用过程中，很难实时监测负载阻力矩的大小，就导致其控制方式实现比较复杂，而且该控制方式的制动距离较长，所以在实际的应用中存在一定的缺陷，不太实用。

最大制动电流控制方式制动电流最大，其制动转矩最大，制动距离最短，但是其能量回馈效率几乎为零，因此违背了节能续航的设计初衷[8-11]。

通过对上面各个控制方法优缺点的总结分析，充分考虑到各个部件的电流和电压的承受力以及制动安全等多方面的因素，选择了基于恒转矩模糊控制策略作为无刷直流电机能量回馈制动的控制策略。该控制方式能提高稳定的制动力矩保证汽车的安全性，且具有较大的能量回馈效率。

3 无刷直流电机能量回馈制动系统仿真

3. 1 无刷直流电机能量回馈制动系统仿真

在MATLAB/Simulink环境中对无刷直流电机进行能量回馈制动系统的仿真。系统总结构图如图7所示[12-14]。

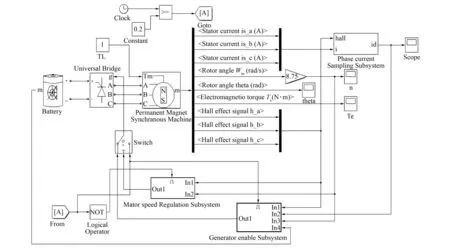
图7 无刷直流电机能量回馈制动系统总仿真模型

其中电机调速模块是电机工作于正转状态下的模块，设定转速为3 000 r/min。此过程主要是为下面能量回馈制动做准备。

本文构造了以给定电流与实际电流的偏差e、电机转速v以及电池的SOC值为输入，以PWM占空比为输出的三输入一输出的三维模糊控制器，来对无刷直流电机能量回馈制动系统进行控制。

能量回馈制动模块是无刷直流电机能量回馈制动系统的核心模块。其内部结构图如图8所示。此模块包含四个输入一个输出：四个输入分别为霍尔信号、电机转速、电机相电流及电池的SOC值，输出为PWM占空比信号。

图8 能量回馈制动模块

其他模块如电机模块、逆变器模块、PWM信号生成模块、逻辑信号和PWM信号整合模块以及相电流取样模块都在以上详细介绍过，在此不再赘述。

3. 2 能量回馈制动系统的仿真结果和分析

在MATLAB/Simulink环境中对建立的无刷直流电机能量回馈制动系统的仿真模型进行仿真。其中电池的初始电压设置为24 V，SOC值设置为30%，设置一个较低的SOC值可以使能量充分进行回收，而不受到电池饱和的限制。在t=0时将电机起动，调节电机的转速，设置电机的转速为3 000 r/min；当t=0.7 s时，控制电机开始降速，降速范围从设定的3 000 r/min降到1 000 r/min，当转速开始降低时，即认为回馈制动状态开起,即在t=0.7 s时，电机由电动状态开始进入能量回馈制动状态。仿真时间设置为1 s,设置制动转矩为2.5 N·m。在此对无刷直流电机进行仿真，结果如图9～图11所示。

图10 电机转矩随时间的变化曲线图

图11 蓄电池SOC值变化曲线图

由图9可以看出，建立的能量回馈制动系统对电机的转速具有良好的调控能力，电机可以按照设置要求在短时间达到目标转速，并且能够在目标转速上保持转速的稳定。设定电机的转速范围为3 000 r/min到1 000 r/min。由图9知道，在t=0 s时控制电机开机旋转，在t=0.3 s左右时达到设定的目标转速3 000 r/min,设置当t=0.7 s时进入电机的制动降速过程，此时电机转速开始下降，并在短时间内降到1 000 r/min。然后保持在1 000 r/min的转速下转动。

由图10可以看出当电机由t=0 s时开起转动，t=0.3 s电机转速在短时间内达到目标转速。加速过程中电机转矩为3 N·m，当达到目标转矩后，电机此时在0.2 s到0.7 s内保持恒转速旋转，此时只需要很小的电机转矩来克服电机内部的摩擦力，从而保持电机在该转速下旋转，如图10所示。此段时间内电机转矩约为0.2 N·m。当t=0.7 s时控制电机降速，此时电机转矩为-2.5 N·m，控制电机降速。其制动转矩如图10中放大图所示。当降速过程结束后，电机保持在1 000 r/min，此时电机转矩又回到0.2 N·m来克服摩擦力保持电机恒速旋转。通过理论对比分析可以发现，仿真得出的电机转矩图与在理论上要求的转矩图完全吻合，说明设计的能量回馈制动系统对电机的转矩具有很强的调控能力。

由图11可知，当电机正转时，电池的电量开始下降，电机加速旋转达到目标转速的过程中，电池电量下降速度较快。当电机保持在目标转矩旋转时，电池电量下降速度略微变慢，这是因为电机加速旋转时，需要较大的加速转矩，此时消耗的能量较大；当电机恒速旋转时，只需要克服电机内部的摩擦力，因此消耗的能量较少。当t=0.7 s时，控制电机降速，此时电池的SOC值停止下降并开始上升，说明能量回馈制动系统开始进行能量回馈。当降速停止时，能量回馈过程结束，此时电池的SOC值停止上升，但电机仍保持旋转，又开始消耗能量，所以电池的SOC值接着开始下降。

通过图9～图11的仿真结果可知，当电机开始降速制动时，本文设计的能量回馈制动系统可以实现恒转矩回馈制动，使得电机的转速可以以较快的速度下降达到设定的转速，并且可以实现高效的能量回收，说明了本文提出的算法和控制策略的可行性和高效性。

4 结 语

本文在对无刷直流电机的回馈制动原理以及控制策略进行深入分析的基础上，采用恒转矩模糊控制策略来对电机能量回馈制动进行控制，设计了一个三维模糊控制器，并在MATLAB环境中用模糊控制器作为控制核心搭建了无刷直流电机能量回馈制动系统的模型。通过仿真可以看出，提出的恒转矩模糊控制策略可以实现能量的回馈制动，并达到了理想的效果。

本文提出的恒转矩模糊控制策略虽然经过仿真验证了理论上可行，但是未考虑到蓄电池最大充电电流、电机工作特性以及各部分的能量传递效率等因素，所以控制策略仍需要进一步完善。

[1] 王成.电动汽车发展对能源与环境影响研究[D].长春: 吉林大学,2007.

[2] 刘卓然,陈健,林凯,等. 国内外电动汽车发展现状与趋势[J].电力建设,2015,36(7): 25-32.

[3] ANONYMOUS. Platform for brushless DC motor driving development[J]. IEEE Trans Electronics Weekly,2010,11(3): 40-44.

[4] GUNDOGDU T, KOMURGOZ G. Self-turning PID control of a brushless DC motor by adaptive interactin[J].IEEE Trans Elec Electron Eng,2014,9(4): 34-37.

[5] 任桂周,常思勤.一种电动汽车能量高效回馈制动方法[J].电网技术,2011,35(1): 164-169.

[6] 苗敬利,李蒙.电动汽车能量回馈制动系统的研究[J].测控技术与仪器仪表,2014,40(8): 94-97.

[7] 瞿道海.电动汽车再生制动能量回馈控制策略的研究[D].长沙: 湖南大学,2014.

[8] LU H P. Research and implementation on control strategy of regenerative braking for pure electric vehicle[J]. IEEE Trans IERI Procedia, 2012,3(10): 26-30.

[9] 刘博,杜继宏,齐国光,等.电动汽车制动能量回收控制策略的研究[J].自动化与仪器仪表,2004,1(1): 34-36.

[10] CORCON P, BUHLER F, NEUMANN I, et al. Energy recapture through deceleration-regenerative braking in electric vehicles from a user perspective[J]. IEEE Trans Ergonomics, 2013,5(68): 57-60.

[11] PENG D, ZHANG Y, YIN C L, et al. Combined control of a regenerative braking and antilock braking system for hybrid electric vehicles[J]. IEEE Trans International Journal of Automotive Technology, 2011,9(6): 58-62.

[12] 查鸿山,李雨桐,刘忠途.电动汽车能量回馈制动仿真研究[J].机械科学与技术,2012,31(4): 572-577.

[13] 刘嘉琦.纯电动汽车能量回馈控制策略与仿真研究[D].长沙: 湖南大学,2013.

[14] 朱慧玲.基于ADVISOR的纯电动汽车制动能量回馈控制策略设计与仿真研究[D].衡阳: 南华大学,2011.

Design on Energy Regenerative Braking System of Brushless DC Motor for Electric Vehicle

ZHAO Jingbo, WANG Daichao, LI Hui, SHI Qi

(College of Automation Engineering, Qingdao Technological University, Qingdao 266520, China)

Put forward a constant torque fuzzy control strategy to solve the problem of low efficiency in electric vehicles energy feedback braking. At first, made the analysis of the basic principles of energy regenerative braking of BLDCM. At the same time, a three-dimensional fuzzy controller through the comparative analysis of the different feedback control strategy was designed, and a BLDCM regenerative braking system simulation model in the MATLAB/Simulink environment was established. Results showed that the control strategy reached good control effects to motor braking torque and energy recuperation.

brushless DC motor; energy regenerative; constant torque; three-dimensional fuzzy controller; electric vehicle

国家自然科学基金项目(51475251)；山东省自然科学基金项目(ZR2013FM014)；山东省高等学校科技计划项目(J12LN37)；青岛市科技计划项目(15-9-2-109-nsh)

赵景波(1971—)，男，博士研究生，副教授，硕士生导师，研究方向为信号处理和控制理论。 王代超(1993—)，男，硕士研究生，研究方向为控制理论。

TM 301.2

A

1673-6540(2017)07- 0129- 07

2016 -12 -19