永磁同步风力发电系统的分数阶比例积分控制算法研究
2017-08-07周小壮王孝洪HOANGTHITHUGIANG
周小壮, 王孝洪, HOANG THI THU GIANG
(华南理工大学 自动化科学与工程学院,广东 广州 510640)
永磁同步风力发电系统的分数阶比例积分控制算法研究
周小壮, 王孝洪, HOANG THI THU GIANG
(华南理工大学 自动化科学与工程学院,广东 广州 510640)
将分数阶比例积分(PIλ)控制器应用于直驱型永磁同步风力发电系统,来达到实现系统高性能控制的目的。重点研究了永磁同步风力发电系统的分数阶PIλ控制器参数设计方法。通过分数阶PIλ控制器系统的仿真研究与试验分析,结果表明:采用分数阶PIλ控制器的系统具有较快的响应速度和较高的功率输出性能,具有一定的发展潜力和实用价值。
分数阶;永磁同步电机;风力发电;最大功率跟踪
0 引 言
在工业控制中,PID控制凭借原理简单、使用方便和适应性强等优点一直占据主导地位。但如果要实现系统的高性能控制,经典的PID控制(整数阶PI控制)就难以实现控制的目标要求。在此背景下,高性能的控制策略成为了研究热点之一。为提高系统控制品质,近年来,分数阶控制器的研究应用吸引了越来越多的关注。在控制领域,可考虑用分数阶控制器来设计整数阶控制对象,从而进一步提高系统的控制性能。分数阶PIλDμ控制器,比经典的PID控制器具有更好的控制性能,这是因为引入了额外的两个参数λ和μ,控制器增加了两个自由度,其对调节系统性能起到了十分重要的作用[1],当μ=0时,即成为分数阶PIλ控制器,是PIλDμ控制器的一种特殊形式。
本文以永磁同步风力发电系统作为控制目标,研究分数阶PIλ控制策略。将三相永磁同步发电机(Permanent Magnet Synchronous Motor,PMSG)作为控制对象,基于分数阶PIλ控制,研究该系统的最大功率跟踪(Maximum Power Point Tracking,MPPT)性能。为了公平地评价分数阶控制器的控制性能,与按照工程整定方法设计的整数阶PI控制器系统的性能进行比较,并进行对比分析,验证设计的有效性。
1 直驱型永磁同步风力发电控制系统构成
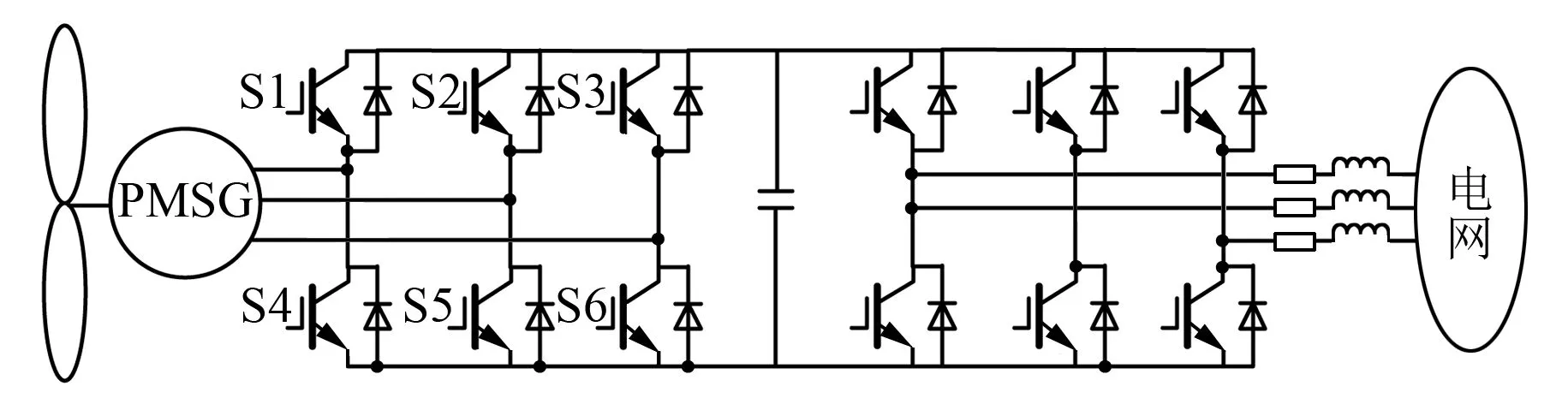
图1 直驱永磁同步风力发电控制系统拓扑结构

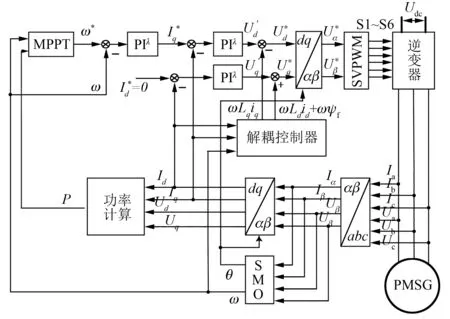
图2 PMSG风力发电控制系统控制原理框图
由式(1)知id和iq之间存在耦合,需进行电流解耦控制,令
将式(2)代入式(1)式,得
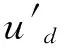
2 分数阶PIλ控制器参数设计
分数阶PIλ控制器的一般形式为
当λ=1时,即成为经典的整数阶PI控制器。
针对永磁同步电机的数学模型,电流内环可等效为一惯性环节:

对于转速外环,可等效为Ⅰ型系统:
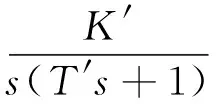
系统开环传递函数为
设系统开环传递函数的截止频率ωc、相位裕度φm均已知,以电流环为例,为了得到良好的系统稳定性和鲁棒性,由截止频率和相位裕度出发,应满足以下三个原则[5]:
FO-PI控制器的频率响应为
其幅值特性和相位特性表示为
arg[C(jω)]=
以电流环为例,根据准则一式(6),有:
根据准则二式(7),有:
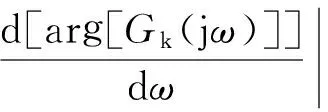
根据准则三式(8),有:

因此可根据式(12)~式(14)来确定Ki、λ、Kp三个参数。
由式(3)解耦后可分别设计电流环和转速环的PIλ控制策略。
系统包含id和iq两个电流环。由于本文采用的是隐极型永磁同步电机,电感Ld=Lq,因此它们的控制对象参数相同,对id和iq可采用相同的分数阶PIλ控制参数,如图3所示,其中具体控制规律为

图3 电流id控制原理图
图3中K=1/Rs,T=Lq/Rs。


图4 转速环控制原理图

本文采用的永磁同步电机参数如下:定子电阻Rs=3 Ω,电感Ld=Lq=40 mH,永磁体磁链ψf=0.53 Wb,极对数p=24,转矩系数KT=1.5pψf。设定系统截止频率ωc=100 rad/s,相位裕度φm=160°,由上述算法得到电流环参数Kpi=5.5,Kii=35,λi=0.8。作出分数阶PIλ控制器下的系统开环bode图如图5所示。由bode图可知,系统在ωc处的相位达到极大值,符合准则二中的鲁棒性要求。
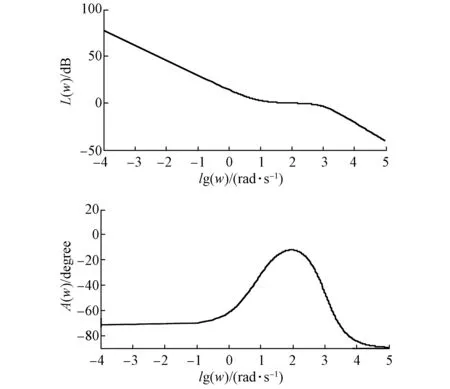
图5 电流环系统开环bode图
由以上设计方法,可先进行电流内环的参数整定,再进行速度外环的参数整定。
3 MPPT设计
为了实现最大功率跟踪的目标,通过判断功率P及转速ω的增量方向输出转速给定ω*[6-9]。整个系统采用功率环、速度环及电流环三闭环控制策略。功率环根据爬山算法输出设定转速,转速环用于实现转速跟踪,电流内环根据转速外环的输出指令完成对电流的控制。
根据风机的运转特性可知,在一定风速ν下,风机输出功率P取决于风能利用系数Cp,在不同的风速下,只有控制风机转速n满足叶尖速比λ=λopt,则Cp(λ)=Cpmax,此时可得到不同风速下的最大功率[10]。功率曲线如图6所示。
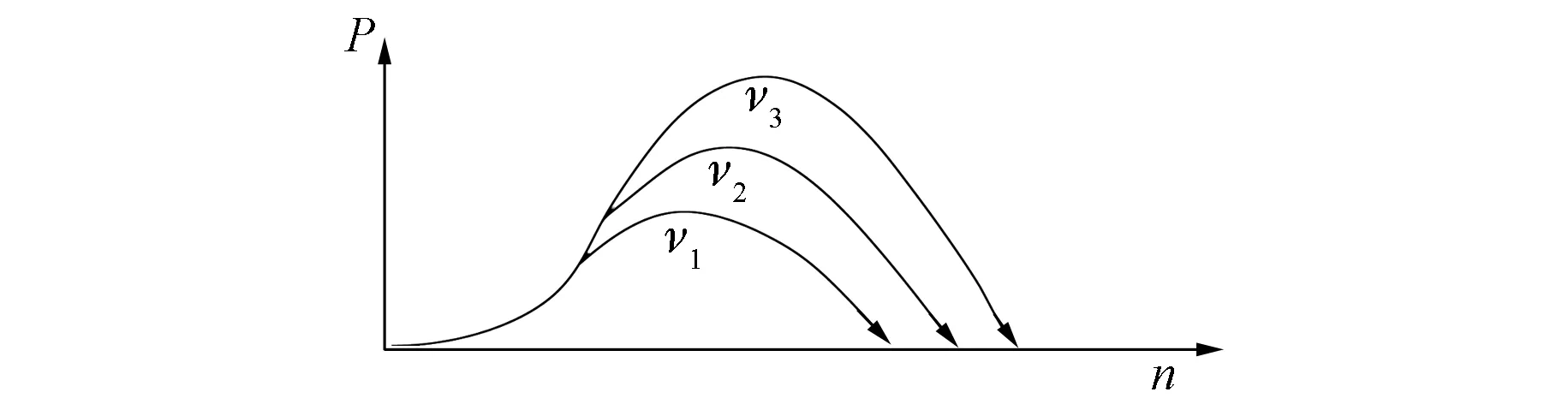
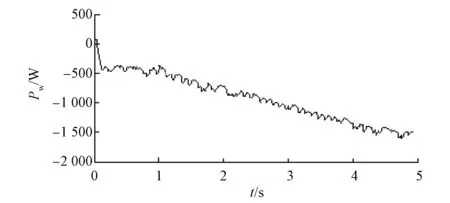
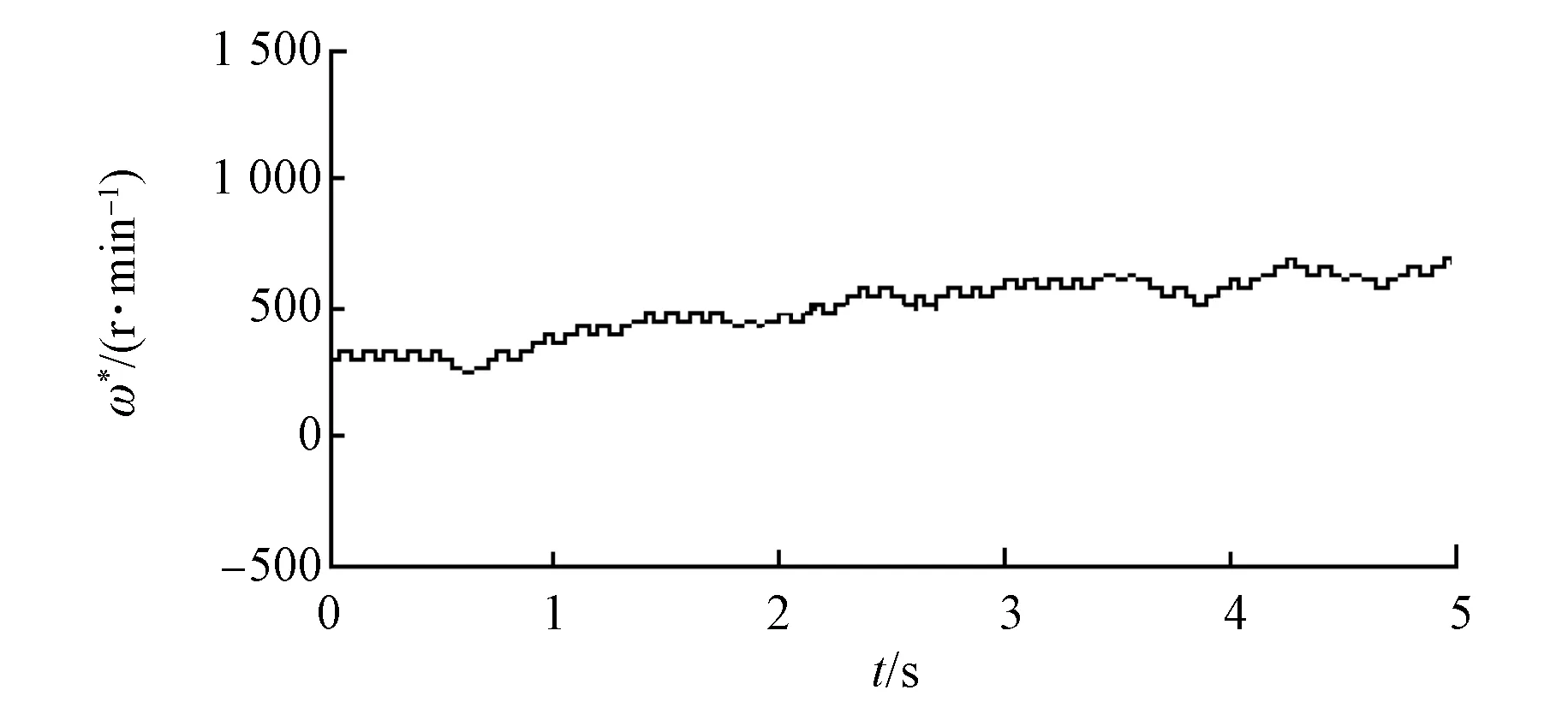
图6 风机特性曲线(v1 本文采用爬山算法来实现最大输出功率跟踪,如图7所示。爬山算法通过对转速给定ω*进行调整,以寻找最佳转速, 然后通过转速控制外环跟踪最佳转速设定值,从而输出最大功率。该算法需要测量功率及转速,从而输出转速控制指令。 图7 爬山算法示意图 图7中功率Pe=1.5(UdId+UqIq),sign为符号函数。 如图6所示,当转速增加,输出功率跟着增加时,可进一步调大转速给定;当转速增加但输出电功率减少时,对转速进行反方向调整。基于爬山法的功率跟踪会使转速输出在最大功率点附近抖动。可通过调整转速变化步长Δω,减少转速抖动,以此来实现最佳效果。 在MATLAB/Simulink环境下进行仿真,检验分数阶PIλ的控制效果。 系统电流环分数阶控制器仿真框图如图8所示。 图8 电流环分数阶控制器 为了测试分数阶控制器的效果,仿真中,观察电机的相电流波形如图9所示。可见电机在 0.05 s内即达到稳定状态,起动速度快,在t=0.15 s时突加负载(50 N·m),电流在0.01 s内到达新的稳定状态,抗扰动性明显,电流调节能力强。 图9 电机起动和突加负载时的相电流波形 为了进一步检验分数阶PIλ控制发电系统的性能,分别在风速不变和风速变化的情况下进行对比仿真试验,观察系统的发电功率输出和转速给定信号。 当模拟风速保持12 m/s恒定不变时,分数阶PIλ控制发电系统功率输出Pw曲线和转速给定ω*曲线分别如图10、图11所示。 图10 风速不变时分数阶PIλ控制系统功率输出 图11 风速不变时分数阶PIλ控制系统转速给定 当模拟风速5 m/s增大到15 m/s(从t=1 s开始增大)时,系统响应曲线分别如图12、图13所示。 图12 风速变化时分数阶PIλ控制系统功率输出 图13 风速变化时分数阶PIλ控制系统转速给定 在风速突变瞬间(t=1 s),系统的功率输出和转速给定波动较小,仅为50 W和50 r/min,随着风速的加大,分数阶系统的输出一直较为平滑,显然,在风速变化等扰动较大的情况,分数阶系统的鲁棒性较强。 分数阶控制系统不仅响应速度快,转速和功率抖动小,而且面对风速变化情况,能较好地结合MPPT模块实现最大功率输出,系统整体输出效能佳,系统鲁棒性强。 图14 发电状态下电机定子电流与位置角 为了检验发电系统的性能,对系统进行发电试验。图14为电机的定子电流与滑模观测器的位置角输出波形,可见定子电流稳定,谐波分量极小,分数阶电流控制器控制效果良好。图15为发电状态下的电网电压与电流波形图。由图15可知,电压与电流反相,发电功率约为2 000 W,尽管此时功率不是太大(额定功率为3 500 W),但是电流正弦度仍然较高,可见尽管在低功率情况下系统仍然具有高性能的电流控制效果。 图15 发电状态下电网电压电流波形 针对直驱型永磁同步风力发电系统,本文设计了基于分数阶PIλ的电流与速度控制器,并进行系统仿真分析与试验。研究表明,基于分数阶的控制系统具有较快的响应速度,基于MPPT时间短,转速给定抖动小,电流控制效果较好,系统的整体性能较高。分数阶PIλ控制器适合于高性能永磁同步风力发电系统,具有一定的实用价值。 [1] 薛定宇,赵春娜.分数阶系统的分数阶PID控制器设计[J].控制理论与应用,2007,24(5): 771-776. [2] 周奕鑫,王孝洪,田联房.双PWM永磁同步风力发电控制器设计[J].电气传动,2014,44(7): 24-29. [3] 陈伯时.电力拖动自动控制系统—运动控制系统[M].3版,北京:机械工业出版社,2009. [4] LI H S, LUO Y, CHEN Y Q. A fractional order proportional and derivative (FOPD) motion controller: tuning rule and experiments[J].IEEE Transactions on Control Systems Technology,2010,18(2): 516-520. [5] 张碧陶,皮佑国.基于分数阶滑模控制技术的永磁同步电机控制[J].控制理论与应用,2012,29(9): 1193-1197. [6] 赵慧敏,李文,邓武.一类分数阶滤波器逼近阶次的选择[J].电机与控制学报,2010,14(1): 90-94. [7] CHEN Y Q. A new discretization method for fractional order differentiators via continued fraction expansion[C]∥2003 ASME International Design Engineering Technical Conferences,Chicago,USA,2003: 1-9. [8] 曹军义,曹秉刚.分数阶控制器的数字实现及其特性[J].控制理论与应用,2006,23(5): 791-794. [9] 白晶.分数阶模型的离散化方法研究[D].大连:大连交通大学,2009. [10] WU B, LANG Y Q, ZARGARI N,等.风力发电系统的功率变换与控制[M].北京:机械工业出版社,2012. Direct-Drive Permanent Magnet Synchronous Generator Wind Turbine System Based on Fractional-Order Controller ZHOU Xiaozhuang, WANG Xiaohong, HOANG THI THU GIANG (College of Automation Science and Engineering, South China University of Technology,Guangzhou 510640, China) In order to achieve high-performance of the control system, fractional-order PIλcontroller was applied to direct-drive permanent magnet synchronous generation (PMSG) wind turbine systems. Focused on the fractional-order PIλcontroller parameters design method of system mentioned above. Through the system simulation and comparative analysis, the result showed that the fractional-order PIλcontroller system had faster response speed and higher power output performance than the integer-order one. The fractional-order PIλcontroller system had certain development potential and practical value in PMSG wind turbine systems. fractional-order; permanent magnet synchronous motor; wind power generation; maximum power point tracking 广东省教育部产学研结合项目(2012B091100299);广东省教育厅科技创新重点项目(2012CXZD0008);广东省高等学校学科与专业建设专项资金(粤财教2010-275);广州市番禺区科技攻关项目(2010-Z-12-04;2011-Z-02-415) 周小壮(1991—),男,硕士研究生,研究方向为自动控制应用。 王孝洪(1976—),男,副教授,硕士生导师,研究方向为电力电子技术及其应用。 HOANG THI THU GIANG(1982—),女,博士研究生,研究方向为电力电子技术及其应用。 TM 315 A 1673-6540(2017)07- 0092- 06 2016 -11 -09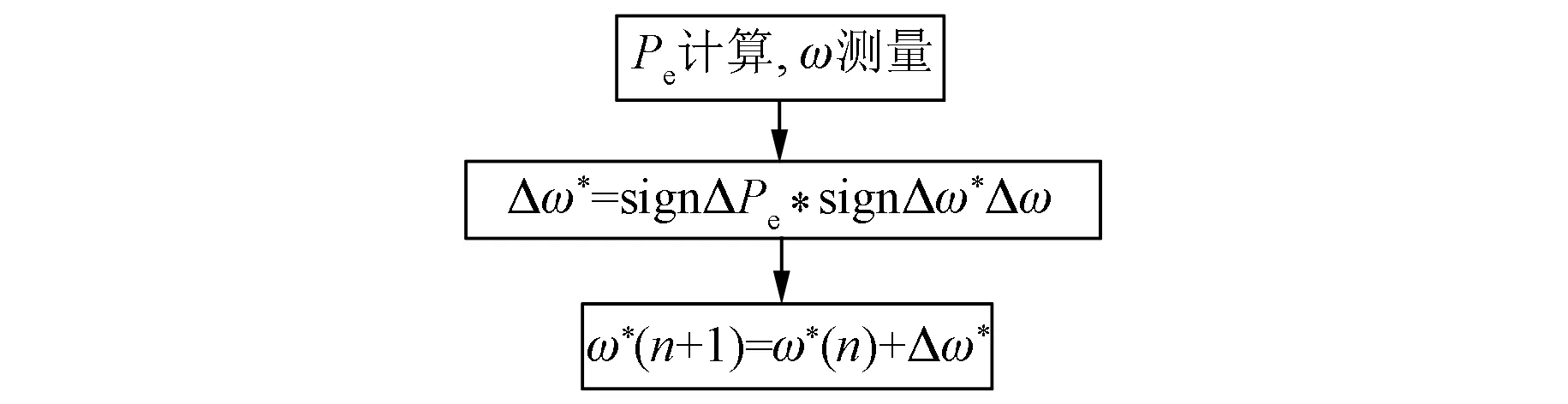
4 系统仿真分析
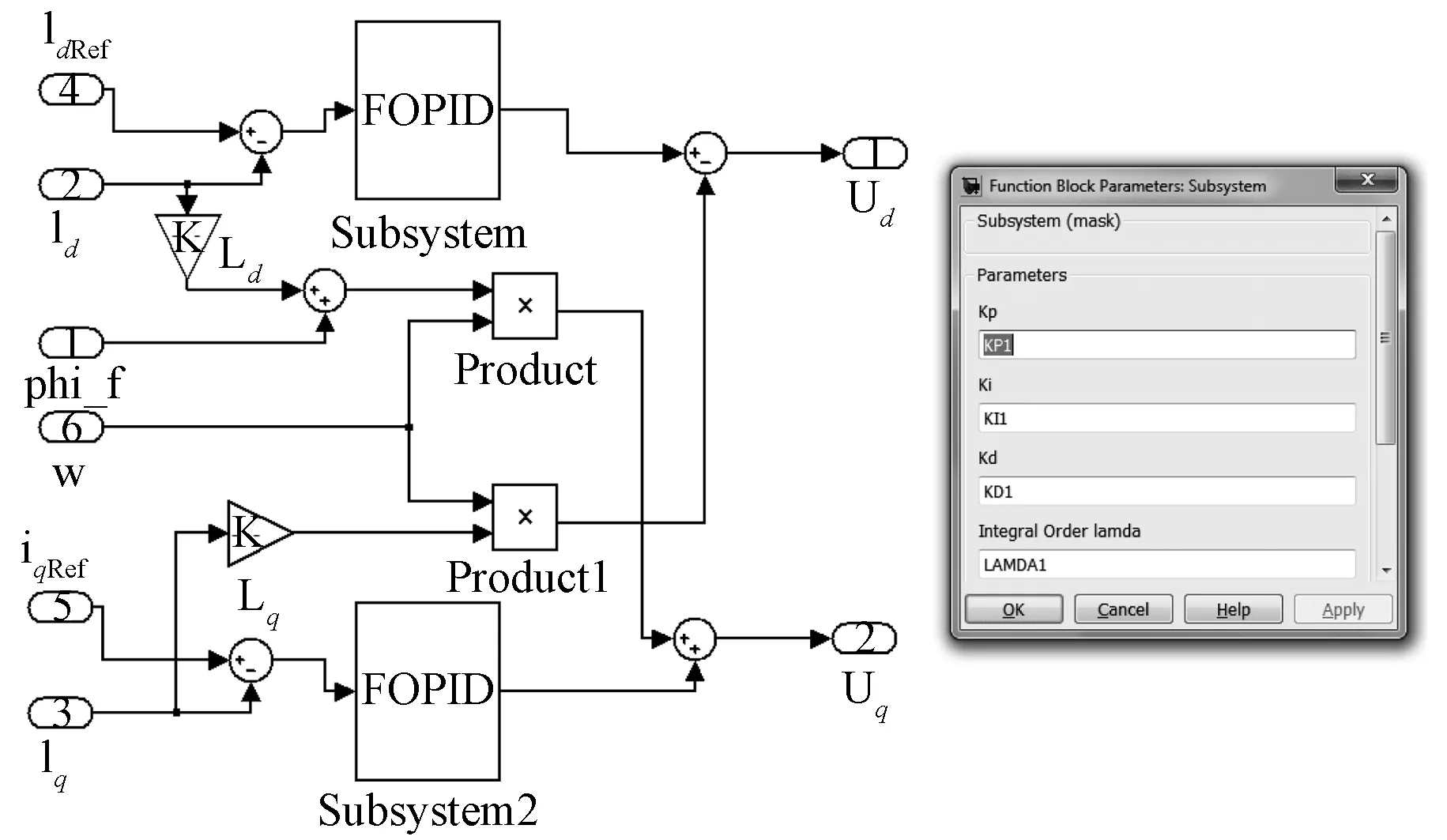

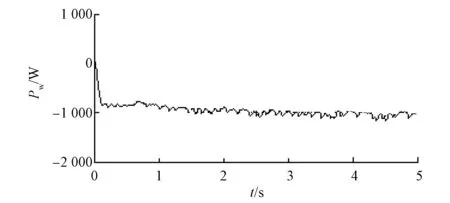
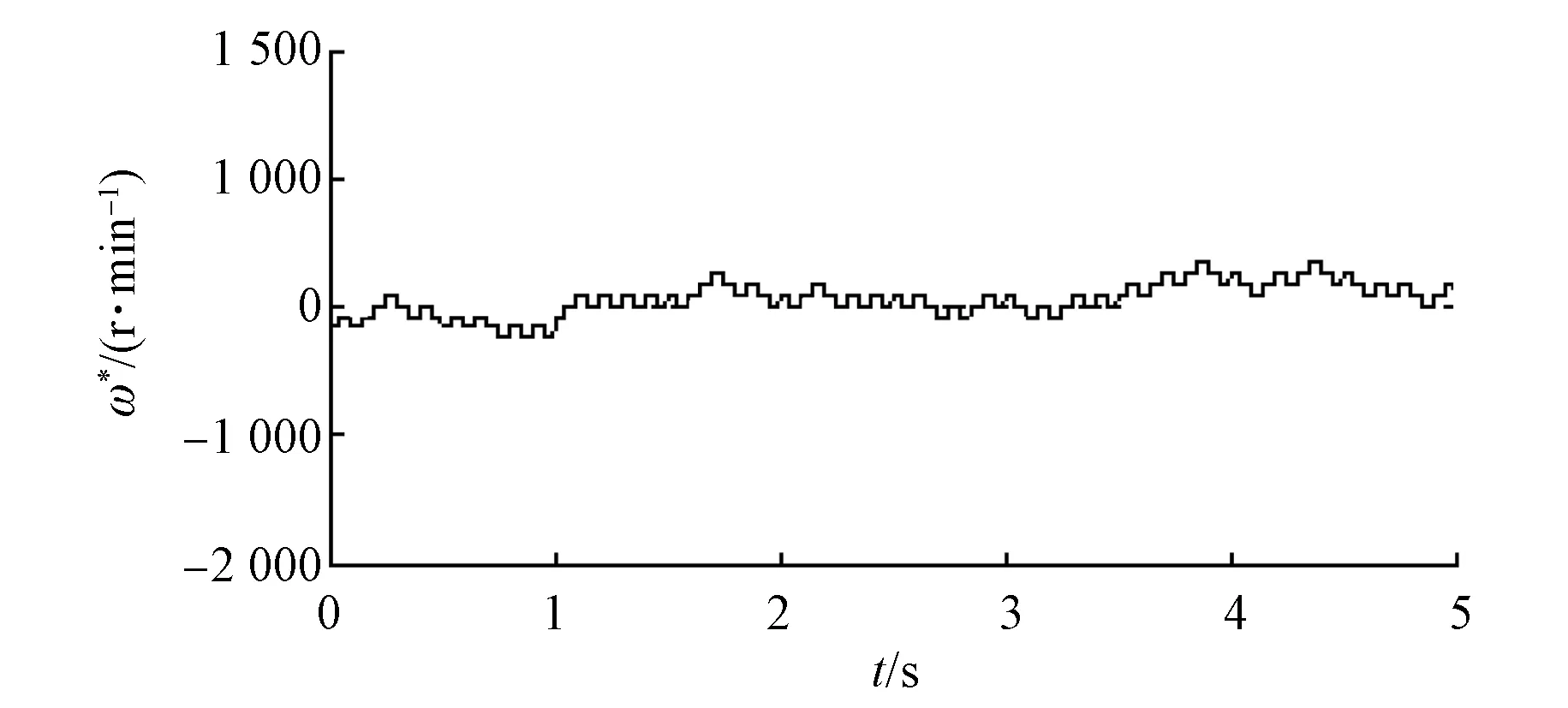
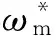
5 系统试验


6 结 语
