基于模型参考自适应参数辨识的永磁同步电机电流预测控制

汪 琦, 王 爽, 付俊永, 李永贵, 冯坚栋

(上海大学 机电工程与自动化学院，上海 200072)

基于模型参考自适应参数辨识的永磁同步电机电流预测控制

汪 琦, 王 爽, 付俊永, 李永贵, 冯坚栋

(上海大学 机电工程与自动化学院，上海 200072)

在永磁同步电机运行过程中，电机参数时变使得电流预测控制器的模型参数和实际电机参数不匹配，导致其控制性能下降。提出了基于模型参考自适应系统(MRAS)的改进电流预测控制方法，利用旋转坐标系下d、q轴电流方程作为参考模型，基于Popov超稳定理论构建永磁同步电机的电感和磁链在线辨识系统，将得到的辨识参数应用于电流预测控制模型中，实现控制模型参数的在线更新。分析与仿真结果表明该方法能够有效地提升在电机参数变化下的电流预测控制性能。

永磁同步电机； 电流预测控制； 辨识参数； 模型参考自适应

0 引 言

永磁同步电机(Permanent Magnet Synchronous Motor，PMSM)拥有高效率、高功率密度、高转矩电流比等优点，被广泛应用于伺服系统[1-2]。PMSM伺服系统需要快速响应的电流内环以保证转速环和位置环的控制性能。传统的电流环控制方式包括滞环控制和比例积分(PI)调节器[3-4]。滞环控制存在开关频率变化大以及纹波较大的问题；PI调节器结构简单，需折衷考虑动态性能与稳态性能，常伴随超调的问题。随着高速数字信号处理技术的发展，需要复杂运算的电流预测控制已经成为PMSM伺服系统研究的热点。

电流预测控制是一种基于电机模型的控制方法，通过选择合适的电压矢量使电流以最优轨迹跟随给定电流，具有响应快、无静差和无超调等优点[5-6]。但电流预测是基于模型的控制方法，对电机参数敏感，而电机在实际运行中，参数会发生改变。文献[7]指出，电机运行时温度及磁路饱和将引起电感以及永磁体磁链的变化，根据永磁材料的不同，永磁体磁链变化幅度将高达20%。文献[8-9]指出，电流预测控制由于控制器模型参数与实际电机参数不匹配会导致电流静差；模型磁链参数不准确会引起q轴电流静差，模型电感参数不准确会引起d轴电流静差。针对电流预测控制模型参数不匹配和实际参数时变的问题，学术界开展了一系列的相关研究。文献[10]提出了一种改进的无差拍预测控制算法，在电机电感参数发生失配的情况下，通过修改电流偏差约束条件和采用输出电压预测方法来提高系统的稳定性。文献[11]在q轴电流预测方程中引入权重因子，使得系统在模型参数不准确时依然保持大范围稳定。文献[12]利用相邻周期的两个预测模型相减来消除恒定项，实现电流的闭环控制，这样可以避免出现稳态误差，同时也消除了磁链失配的影响。文献[13]建立电感、磁链与d、q轴电流之间的函数关系，并通过试验离线测量和绘制出图表形式，应用于参数可调的电流预测控制中，消除了参数不准确的问题。

本文基于模型参考自适应系统(Model Reference Adaptive System，MRAS)对电机的永磁体磁链及电感进行在线辨识，并将辨识结果应用于电流预测控制策略中，实现电流环的自适应预测控制。

1 电流预测控制

PMSM是一个多变量、强耦合、非线性的系统。为了便于分析，假设磁路不饱和，磁场在空间呈正弦分布，不计磁滞及涡流损耗，在dq坐标系下PMSM的电压方程为

式中：ud、uq、id、iq——d、q轴的电压和电流；Ld、Lq、Ψd、Ψq——d、q轴的电感和磁链；Ψf——永磁体磁链；ωe、Rs——转子电角速度和定子电阻。

选取id、iq为状态变量，得到电机的状态方程：

在伺服控制系统中，由于控制周期T很小，因此可认为在每个采样周期T中，输出的转速保持不变。采用一阶欧拉法对式(2)进行离散化，得

式(3)移项后得到离散电压方程：

对于表贴式PMSM有Ld=Lq=L。

假设d轴和q轴的参考给定电流值分别为idr和iqr，则电流预测的目标是使得在一个调制周期后，电流的实际值等于给定值，因此令id(k+1)=idr，iq(k+1)=iqr，将其代入式(4)中得到：

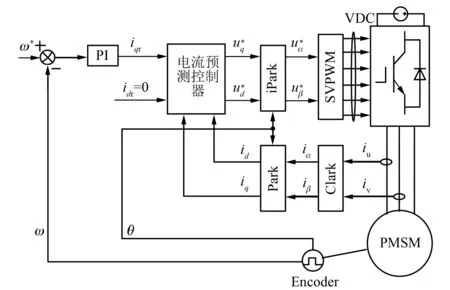
图1 PMSM电流预测控制系统框图

本文所提出的电流预测控制结构如图1所示。其中电流预测控制器根据式(5)搭建，根据电流指令值和当前电机的运行状态计算出使电机电流跟随给定电流所需要的电压矢量uq(k)和ud(k)。将电压矢量通过SVPWM调制，生成所需要的开关信号作用于逆变器。

针对表贴式PMSM，设实际的电机参数为Rs0、Ld0=Lq0=L0、Ψf0，电流预测控制器的参数为Rs、Ld=Lq=L、Ψf。通过式(5)计算的电压矢量uq(k)和ud(k)作用于实际的电机，可用式(3)表示一个控制周期内实际电机电流的响应。把式(5)代入式(3)，有：

式中： ΔRs,ΔL,ΔΨf——控制器参数与实际电机参数的差值,ΔRs=Rs-Rs0，ΔL=L-L0，ΔΨf=Ψf-Ψf0。

实际控制系统中T一般是10-4数量级，Rs一般为10-1数量级，L一般在几到几十mH的数量级，因此认为TΔR≪ΔL，可以忽略电阻变化的影响。

2 基于MRAS的改进电流预测控制

电流预测控制是基于模型的控制方法，因此控制器中模型参数的不准确对控制性能有很大影响。本文基于MRAS对电机参数进行在线辨识，并将辨识结果应用于电流预测控制器模型，从而提升参数变化下电流控制系统性能。

MRAS通过将具有相同输入u的可调模型与参考模型的输出量进行比较产生一个误差信号e，然后将误差信号通过合适的自适应律来不断地调节可调模型中的参数，使其误差信号为零，此时可调参数就逼近参考模型即实际电机的参数。其基本结构如图2所示。

图2 MRAS辨识结构框图

参考模型即实际电机模型如式(2)所示，将其写成矩阵方程并简写为如下形式：

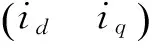
基于状态方程构造PMSM的参数调整模型：

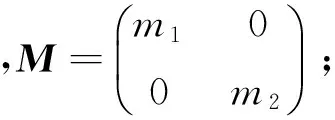
m1、m2——有限的正实数。

将参考模型式(7)减去可调模型式(8)，得到误差状态方程：

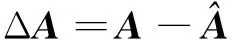
根据误差状态方程式(9)，可以看出这是一个标准的反馈系统，由一个线性定常的正向环节与一个非线性反馈环节组成，如图3所示。为了简化系统的运算，令图3中的D为单位矢量。用一个非线性反馈系统将自适应矢量V和反馈矢量W相连接，这样就组成了等效的反馈系统。其中W=-W1。

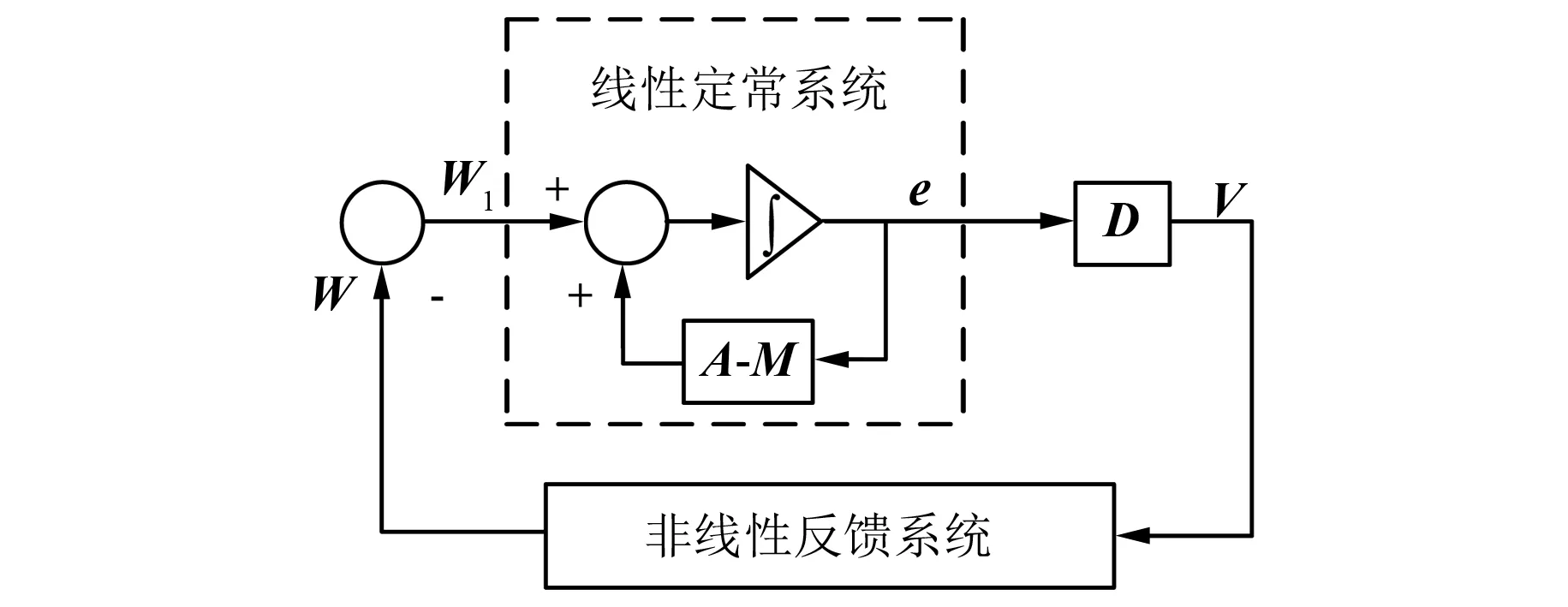
图3 非线性反馈系统框图

为保证系统的全局稳定，利用Popov超稳定理论对MRAS系统进行设计。根据Popov超稳定理论，若使系统逐渐稳定，必须使得非线性反馈系统满足下面的积分不等式[14]：

式中:γ是个有限的正实数，VT=eT。 将V和W代入式(10)中，可以得到:

将式(11)进行展开并分解得到第一个积分项为

为了保证式(12)成立，根据传统形式的自适应规则，一般选择积分加比例的形式，因此整理后可得

式中：L(0)——电感初始值。

同理也可以推导出另外一个积分项的自适应律如式(14)所示。其中Ψ(0)是磁链的初始值。

3 仿真验证

图4 基于MRAS的电流预测控制系统框图

本文提出的基于MRAS的改进电流预测控制算法原理框图如图4所示。转速环采用PI控制策略，电流环采用电流预测控制策略。将MRAS辨识得到的电感和磁链应用于电流环的电流预测控制器中，使得电流预测控制器的模型参数与实际电机参数相匹配。根据图4的控制结构框图，本文通过MATLAB/Simulink搭建离散的仿真模型来验证所提出基于MRAS参数辨识的PMSM电流预测控制算法。

仿真模型中，电机的各项参数如表1所示。

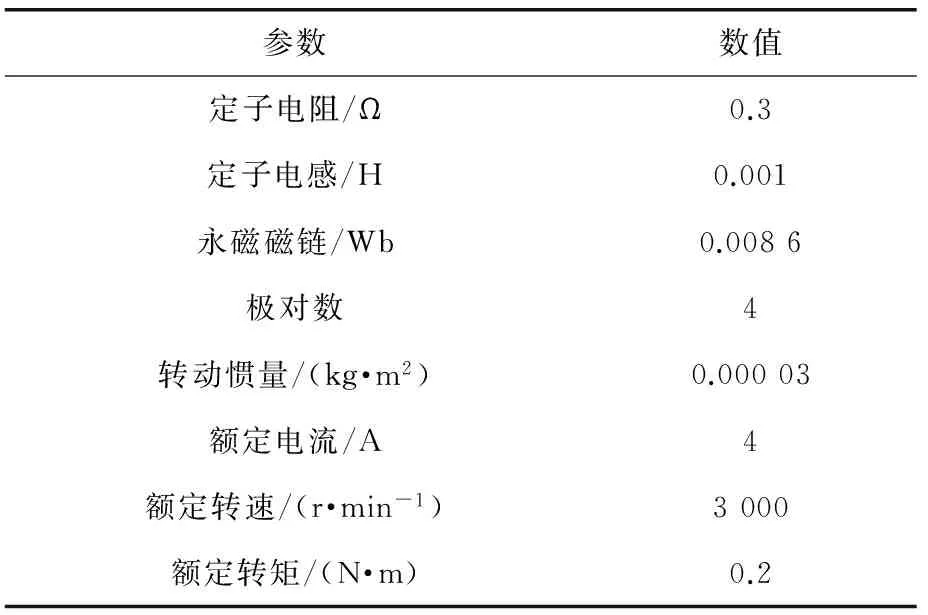
表1 电机参数

设定电机的给定转速为1 000 r/min，逆变器的开关频率是10 kHz。电感及磁链的初始值分别设定为0.002 H、0.01 Wb。

电机电感和磁链的辨识波形如图5～图6所示。可以看出，在t=15 ms左右，电感和磁链的辨识结果收敛于实际值。

图5 电感辨识值与真实值

图6 磁链辨识值与真实值

电机实际运行过程中，根据文献[7]研究发现，电感随着温度上升而增大，磁链随着温度上升而减小，磁链最高会出现20%的变化。模拟实际工况，仿真中在t=0.05 s到t=0.15 s这个时间段内，设置电感从0.001 H变为0.001 2 H，增大20%，设置磁链从0.008 6 Wb变为0.007 74 Wb，减小10%，辨识算法的跟踪特性如图7～图8所示。从图7～图8中可以看出即使电机参数在电机运行过程中发生改变，辨识的结果也能够跟上电机参数的实际值。

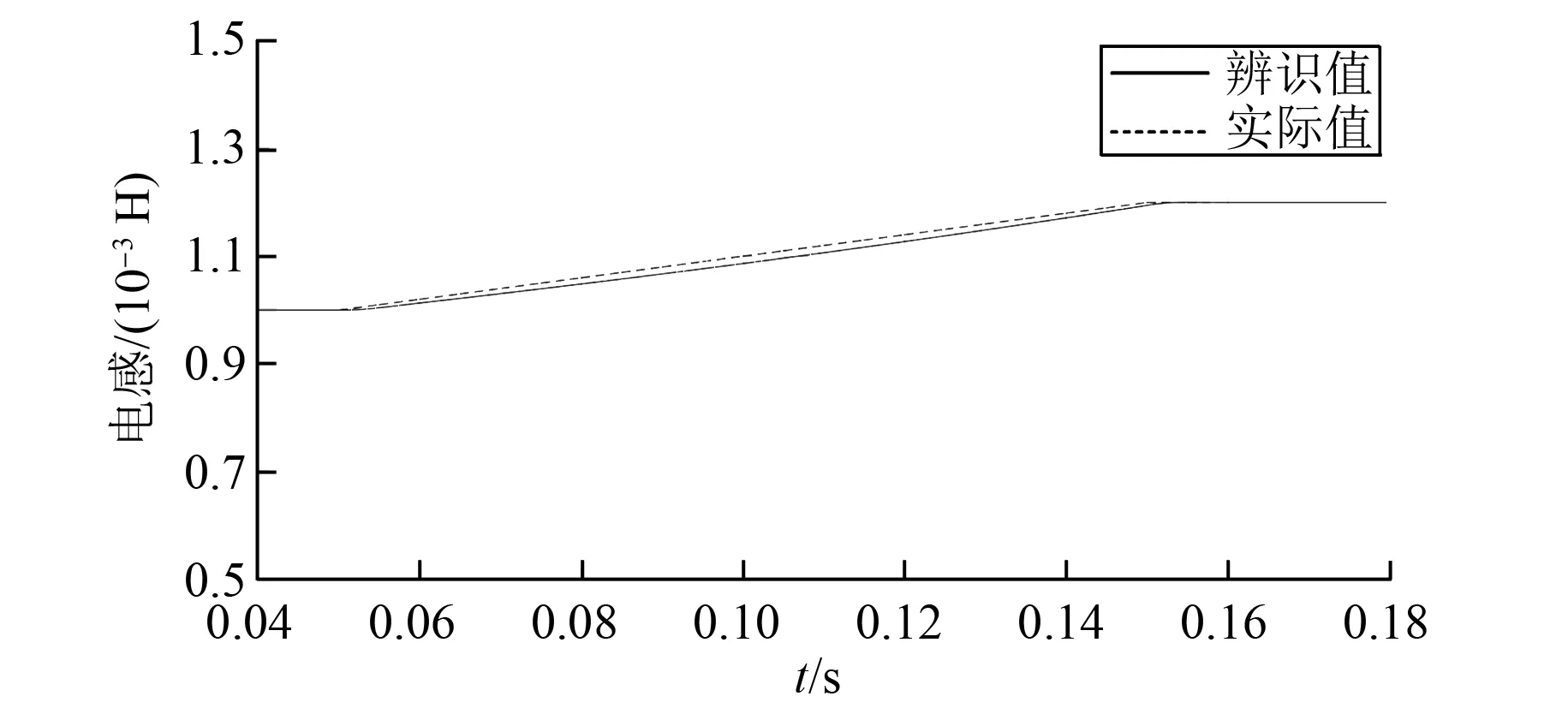
图7 电感变化时跟踪特性

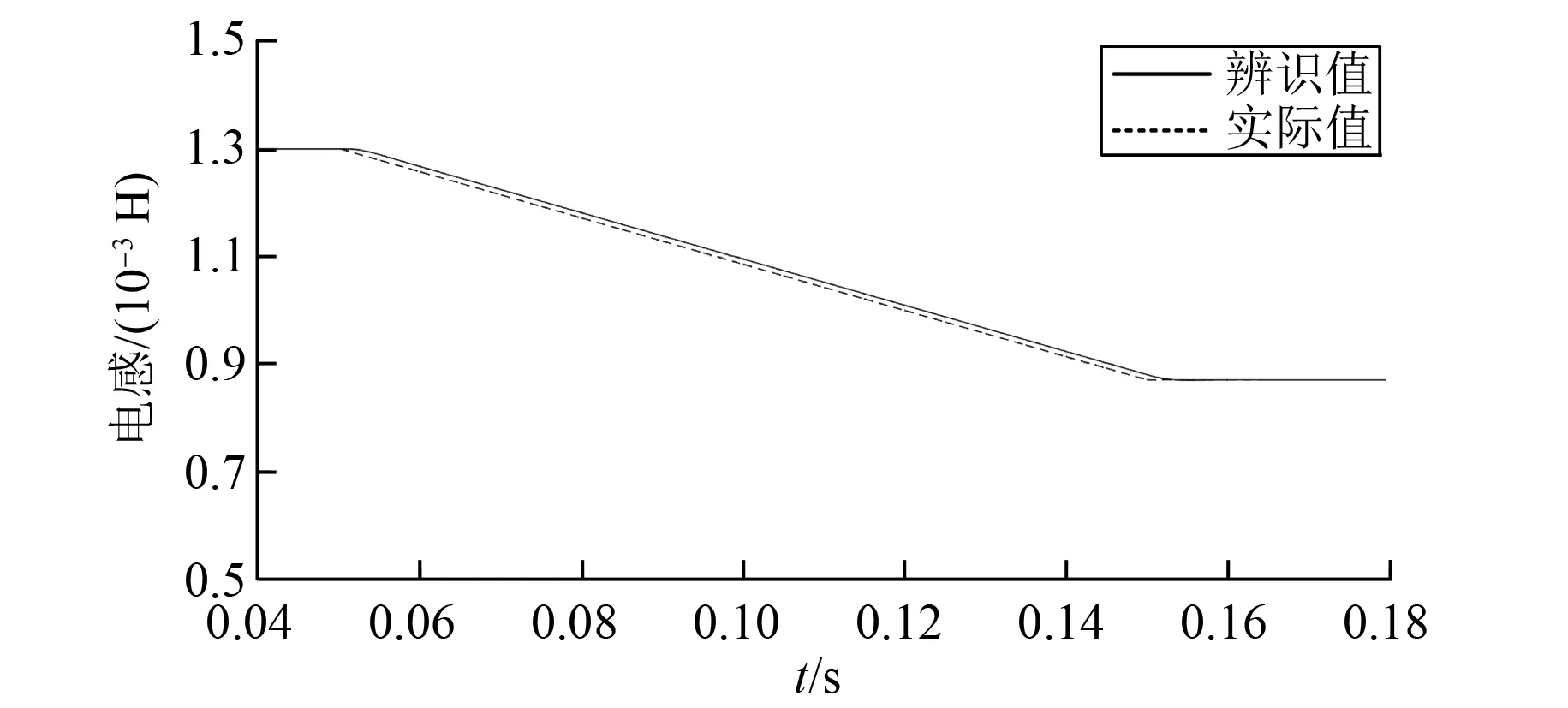
图8 磁链变化时跟踪特性

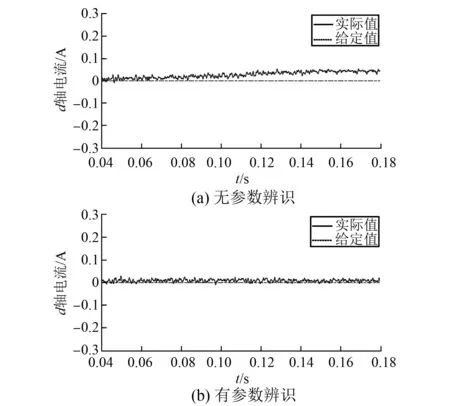
图9 电感改变时d轴电流响应波形

图9(a)、图9(b)与图10(a)、图10(b)分别为电感与磁链发生变化时，电流预测控制无参数辨识与有参数辨识时的电流响应波形。

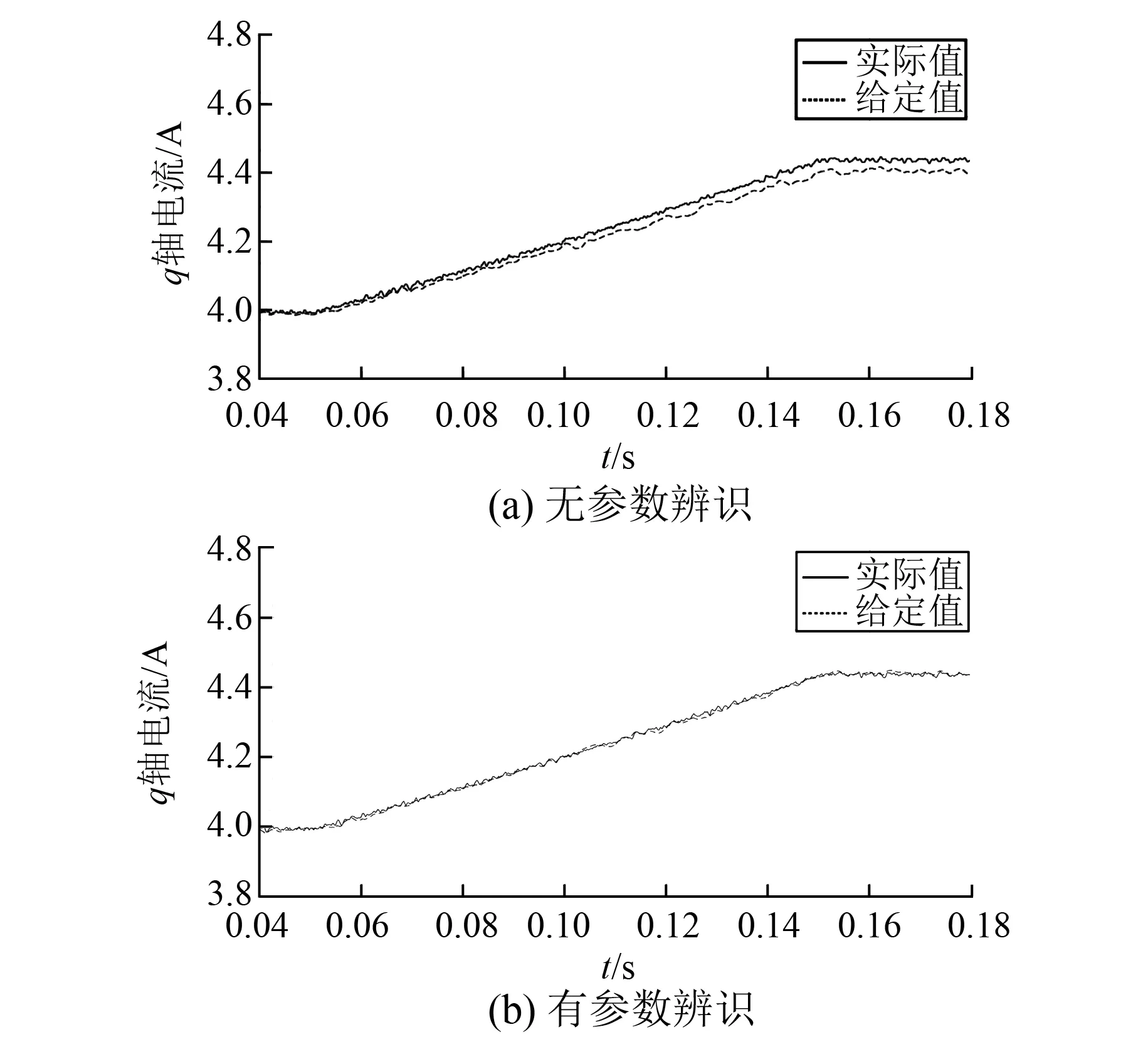
图10 磁链改变时q轴电流响应波形

从图9(a)可以看出，在0.05 s到0.15 s时间段内，电感参数的变化引起电机d轴电流响应出现静差，静差随电感参数增大而变大，0.15 s后电机电感保持不变，静差也保持恒定；图9(b)是采用MRAS算法后d轴电流响应波形，可以看出在参数变化过程中，d轴电流响应没有了静差。

从图10(a)可以看出，在0.05 s到0.15 s时间段内，磁链参数的变化引起电机q轴电流响应出现静差，静差随磁链参数减小而变大，同时由于磁链的减小，会引起q轴电流的变大；0.15 s后电机磁链保持不变，静差也保持恒定；图10(b)是采用MRAS算法后q轴电流响应波形，可以看出在参数变化过程中，q轴电流响应没有了静差。

4 结 语

电流预测控制逐步在永磁伺服驱动中开展应用，运行过程中电机参数的变化限制了基于模型的预测控制算法性能。为此，本文提出了一种基于MRAS参数辨识的改进电流预测控制方案，通过构建电感和磁链的在线辨识算法，实现电流预测控制器的模型参数的实时更新，从而提升电机参数变化下的系统性能。仿真结果验证了该方法的有效性。

[1] 王爽,朱文举,黄苏融,等.采用卡尔曼滤波器的PMSM改进预测函数控制[J].电机与控制学报,2015,19(7): 88-94.

[2] 王伟华,肖曦.永磁同步电机电流增量预测算法参数设计及性能分析[J].电机与控制学报,2013,17(12): 98-105.

[3] 余文涛,胡育文,郝振洋,等.一种改进型永磁电机数字电流滞环控制方法[J].电气传动,2010,40(2): 29-32.

[4] BOLOGNANI S, BOLOGNANI S, PERETTI L, et al. Design and implementation of model predictive control for electrical motor drives[J].IEEE Transactions on Industrial Electronics,2009,56(6): 1925-1936.

[5] MOON H T, KIM H S, YOUN M J. A discrete-time predictive current control for PMSM[J].IEEE Transactions on Power Electronics,2003,18(1): 464-472.

[6] 高丽媛,卢达,赵光宙,等.应用自动微分的永磁同步电机预测控制[J].电机与控制学报,2012,16(10): 38-43.

[7] 李红梅,陈涛.永磁同步电机参数辨识研究综述[J].电子测量与仪器学报,2015,29(5): 638-647.

[8] 王伟华,肖曦.永磁同步电机高动态响应电流控制方法研究[J].中国电机工程学报,2013,33(21): 117-123.

[9] 王庚,杨明,牛里,等.永磁同步电机电流预测控制电流静差消除算法[J].中国电机工程学报,2015,(35)10: 2544-2551.

[10] 王宏佳,徐殿国,杨明.永磁同步电机改进无差拍电流预测控制[J].电工技术学报,2011,26(6): 39-45.

[11] 牛里,杨明,刘可述,等.永磁同步电机电流预测控制算法[J].中国电机工程学报,2012,32(6): 131-137.

[12] 王伟华,肖曦,丁有爽.永磁同步电机改进电流预测控制[J].电工技术学报,2013,28(3): 50-55.

[13] ANGELONE G, PIZZO A D, SPINA I, et al. Model predictive control for PMSM with flux-current nonlinear maps[C]∥ International Symposium on Power Electronics,Electrical Drives,Automation and Motion,2014: 848-853.

[14] 王成元,夏加宽,孙宜标.现代电机控制技术[M].北京: 机械工业出版社,2008.

Predictive Current Control for Permanent Magnet Synchronous Motor Based on Model Reference Adaptive System Parameter Identification

WANG Qi, WANG Shuang, FU Junyong, LI Yonggui, FENG Jiandong

(School of Mechatronics Engineering and Automation, Shanghai University, Shanghai 200072, China)

During the operation of permanent magnet synchronous motor (PMSM), parameter mismatches caused by time-varying motor parameters between real motor and model in predictive current controller lead to the degradation of the control performance. Presented an improved predictive current control method based on the model reference adaptive system (MRAS).d,q-axis current equation in the rotating coordinate system was utilized as a reference model in this method. Based on Popov’s hyper-stability theory, online identification system of inductance and flux for PMSM was established. The identification parameters obtained were used in the predictive current control model, thus online updating of the control model parameters was achieved. Analysis and simulation results showed that this method efficiently improved the performance of predictive current control under the motor parameters change.

permanent magnet synchronous motor (PMSM); predictive current control; identification parameter; model reference adaptive system (MRAS)

汪 琦(1992—)，男，硕士研究生，研究方向为电力电子与电力传动。 王 爽(1977—)，男，博士研究生，研究方向为电力电子与电机驱动控制。

TM 351

A

1673-6540(2017)07- 0048- 06

2016 -12 -12