柯西中值定理“中值点”的渐近性

赵自强, 李冬辉

(河南教育学院 数学与统计学院，河南 郑州 450046)

柯西中值定理“中值点”的渐近性

赵自强, 李冬辉

(河南教育学院 数学与统计学院，河南 郑州 450046)

在较弱条件下讨论了柯西中值定理“中值点”的渐近性，得出了具有一般形式的结果.同时作为推论，得出拉格朗日中值定理“中值点”渐近性具有一般形式的结果.

柯西中值定理；拉格朗日中值定理；中值点；渐近性

0 引言

对于柯西中值定理“中值点”的渐近性，文献[1-5]进行了研究.本文将文献[1]中对具有高阶导数的要求放宽，在较弱条件下研究柯西中值定理“中值点”的渐近性，得出了具有一般形式的结果.作为此结果的一个特例，得出拉格朗日中值定理“中值点”渐近性具有一般形式的结果.首先，引述拉格朗日中值定理和柯西中值定理.

拉格朗日中值定理设函数F(x)在闭区间[a,b]上连续，在开区间(a,b)内可导，则在(a,b)内至少存在一点ξ，使得等式

F(b)-F(a)=F′(ξ)·(b-a)

成立,其中ξ称为拉格朗日中值定理的中值点.

柯西中值定理设函数F(x)和G(x)在闭区间[a,b]上连续，在开区间(a,b)内可导，且在(a,b)内G′(x)≠0，则在(a,b)内至少存在一点ξ，使得等式

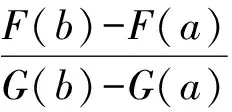
(1)

成立，其中ξ称柯西中值定理的中值点.

1 主要定理

证明构造辅助函数

由洛必达法则和定理条件，得

(2)

又由(1)式及拉格朗日中值定理，得

其中ξ和ζ分别为介于a与x之间的柯西和拉格朗日中值定理的中值点.

由于G′(x)在点a连续且G′(x)≠0，得

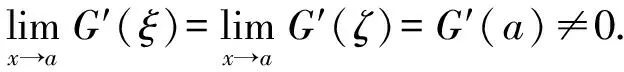
所以

再由定理的条件，得

(3)

所以，由(2)，(3)式，得

2 一些推论

推论1设函数F(x)在a的某邻域U(a,δ)内具有直到n阶导数，

F(i)(a)=0(i=1,2,…,n;n≥1)，

F(n+1)(a)存在，在U(a,δ)内G(x)可导且G′(x)≠0，G′(x)在a处连续，则当F(n+1)(a)≠0时，对于柯西中值定理确定的中值点ξ有

证明由推论的条件，连续应用洛必达法则，得

由定理，得

在定理中，取G(x)=x,则有

[1] 高国成.微分中值定理“中间点”的渐近性[J].工科数学，2001,17(5):102-104.

[2] 刘文武,严忠权.积分型Cauchy中值定理中间点的渐近性[J].数学的实践与认识，2010,40(11):228-231.

[3] 王金花,孙兰香,朱江红.泰劳公式的拉格朗日型余项中值点的研究[J].数学的实践与认识，2010,40(7):221-224.

[4] 戴立辉.刘龙章.积分型Cauchy中值定理中间点的渐近性[J].大学数学，2009,25(3):168-172.

[5] 李冬辉.具有Lagrange型余项的Taylor定理中值点的渐近性[J].河南教育学院学报(自然科学版)，2016,25(3):1-3.

AsymptoticPropertyofIntermediatePointonCauchyMeanValueTheoremforDifferentials

ZHAO Ziqiang， LI Donghui
(SchoolofMathematicsandStatistics,HenanInstituteofEducation,Zhengzhou450046,China)

Studied the asymptotic properties of intermediate point on the mean value theorem for differentials, and the results are obtained.

Cauchy mean-value theorem; Lagrange mean-value theorem; intermediate point; asymptotic property

2017-03-20

河南省教育厅科技项目(16B110056)

赵自强(1981—)，男，河南沈丘人，河南教育学院数学与统计学院讲师.

10.3969/j.issn.1007-0834.2017.02.002

O172.2

：A

：1007-0834(2017)02-0005-03