基于量子随机行走的两光子Bell态测量

李小曼，李大创，杨 名,曹卓良

(1.安徽大学 物理与材料科学学院， 安徽 合肥 230039； 2.合肥师范学院 电子信息工程学院，安徽 合肥 230601)



基于量子随机行走的两光子Bell态测量

李小曼1,2，李大创1,2，杨 名1,曹卓良1,2

(1.安徽大学 物理与材料科学学院， 安徽 合肥 230039； 2.合肥师范学院 电子信息工程学院，安徽 合肥 230601)

量子纠缠态是量子信息和量子通讯领域中的核心资源，实现量子纠缠态中的完全Bell态测量，将对量子信息学的发展有重要的意义。本文，我们基于量子随机行走提出了一种实现双光子Bell态测量的物理方案。基于该方案的操作过程有明显的简化，本方案在实验上具有一定的可行性和指导意义。

量子随机行走；Bell态；量子信息；量子纠缠

在量子信息处理和量子通讯领域中，量子纠缠[1,2,3]具有很重要的地位。量子纠缠，尤其是纠缠光子由于其在传输过程中不易发生退相干，在实现诸如量子纠缠交换[4,5]、量子隐形传态[6,7]和远程态制备[8]之类量子信息处理方案中都起着至关重要的作用。

1995年，Kwiat[9]等人利用自发参数下转换方法实验上制备了两光子偏振纠缠Bell态。Zeilinger[10]等人基于线性光学利用两个纠缠光子对产生一个三光子Greenberger-Horne-Zeilinger(GHZ)态的思想。如何区分正交的量子态在量子信息领域中愈来愈重要。目前为止，国内外的研究组提出了多种区分处于偏振纠缠的Bell态及三光子GHZ的方案[11]。例如，2005年Barrett[12]等提出的基于弱非线性实现非破坏性的Bell态分析方案。最近，林秀敏[13]等先后提出了基于腔场和法拉第旋转的Bell态分析器及GHZ态分析器，成功地实现对两光子Bell态及三光子GHZ态的非破坏性区分。

本文中，首先提出一个基于量子随机行走实现非破坏性测量两光子Bell态方案。在此方案中，通过对探测器进行测量就可以对四个处于偏振纠缠的Bell态进行完全且非破坏性的区分。先前的实验方案中利用偏振分束器，该方案利用常见的光学器件，如：半波片(HWPs)、光束偏转器(BDs)，在实验上能够很容易实现。

1 基于量子随机行走的双光子Bell态测量

在这一部分中，我们将设计一个量子随机行走的物理方案来区分四个Bell态。在设计方案中，我们把四个Bell态作为量子随机行走的硬币态，经过三步行走之后，我们通过测量光子的位置就可以区分出部分Bell态。

我们简单回顾一下一维分离量子随机行走[14,15,16]概念，系统联合希尔伯特空间可以用硬币空间和位置空间来描述，即H≡HC⊗HP。其中硬币空间由正交矢量{|n〉p,n∈Z}展开，表示该粒子处在直线上的位置；硬币空间由正交矢量{|H〉C,|V〉C}来表示，表示的是硬币的状态。粒子的初态可以写成|Ψ(0)〉=|Ψ(0)〉C⊗|Ψ(0)〉P，其中|Ψ(0)〉C为硬币初始态，|Ψ(0)〉P为位置初始态。

不失一般性，我们通常假设粒子从x=0开始运动，并且硬币初始态处于|H〉和|V〉的相干叠加态。如果粒子的初态是|Ψ(0)〉，经过t步行走，粒子的末态：|Ψ(t)〉=Ut|Ψ(0)〉。

现在，我们考虑两个粒子的量子随机行走，系统的联合希尔伯特空间：

H12≡H1⊗H2≡(HC1⊗HP1)⊗(HC2⊗HP2)，

其中，H1表示粒子1的希尔伯特空间，H2表示粒子2的希尔伯特空间。

两个粒子的量子随机行走的演化算符：

U12=U1⊗U2，

其中，U1和U2的定义与单个粒子的U的定义类似。

假设两个粒子的初始位置都在x=0，两个粒子的硬币初始态为任意纠缠态|Ψ(0)〉C12=α1|H〉1|H〉2+α2|H〉1|V〉2+α3|V〉1|H〉2+α4|V〉1|V〉2，系数满足归一化条件，那么系统的初态为：

双光子偏振Bell态可以写成：

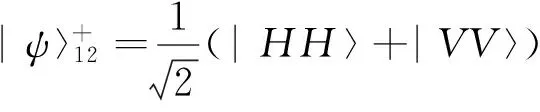
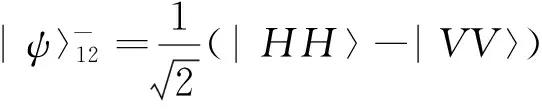
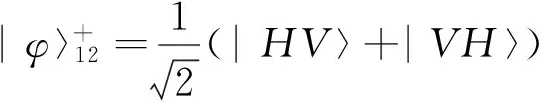
我们将双光子的偏振自由度和位置自由度作为量子随机行走的硬币自由度和位置自由度，初始硬币态是四个Bell态中的其中一个，两个光子初始位置都在x=0。那么，系统的初始态为：

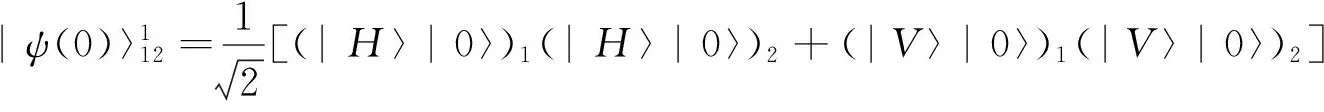
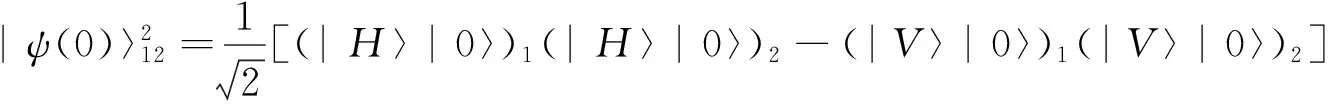
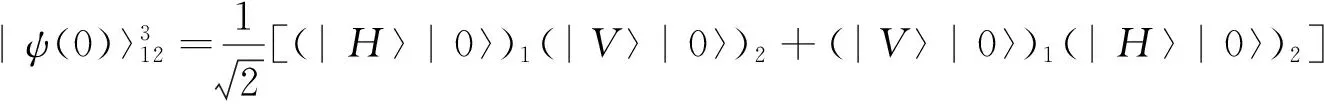
双光子量子随机行走的3步演化过程如图1所示。在我们所设计物理方案中，硬币算符可以用半波片(HWPs)来实现，位置移动算符可以用光束偏转器(BDs)来实现。

图1 实现Bell态测量光路图

第一步，硬币算符为：

其余的为单位算符I。其中，硬币算符为Ci,j，下标i=1,2,3表示第几步操作，j=1,2代表对从第几个分支出来光子的操作。每一个位置移动算符都为S。

第二步，硬币算符仅仅是NOT门操作，即：

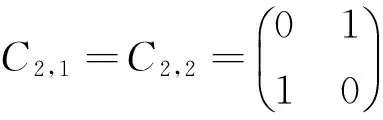
第三步，硬币算符是Hadamard门操作，即：

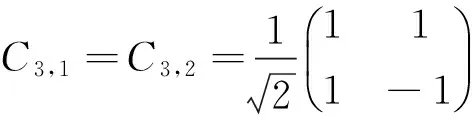
经过第一步行走，系统的状态为：

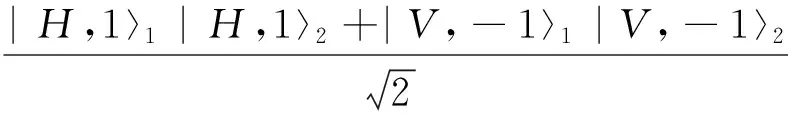
经过了一步行走，我们交换两光子在x=-1的线路，这是我们所设计的物理方案的重要组成部分，可以在两光子之间产生线路纠缠，并且在实验上很容易实现。经过了线路交换，两光子演化为：

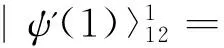
两步量子随机行走之后，由于两光子的空间波函数完全叠加，根据全同性原理可得：

(|H〉|0〉)1(|V〉|0〉)1+(|H〉|0〉)2(|V〉|0〉2)+(|V〉|0〉)2(|H〉|0〉2)],

(|H〉|0〉)1(|V〉|0〉)1-(|H〉|0〉)2(|V〉|0〉2)

-(|V〉|0〉)2(|H〉|0〉2)], 经过了第三步演化，系统的末态为：

(|V〉|-1〉)1(|V〉|-1〉)1+

(|H〉|1〉)2(|H〉|1〉)2-

(|V〉|-1〉)2(|V〉|-1〉)2],

(|V〉|-1〉)1(|V〉|-1〉)1

-(|H〉|1〉)2(|H〉|1〉)2+

(|V〉|-1〉)2(|V〉|-1〉)2],

(|V〉|-1〉)1(|V〉|-1〉)2)],

(|V〉|-1〉)1(|H〉|1〉)2)].

2 讨论和结论

经过三步量子随机行走，我们对两个光子进行探测，如果两光子从同一分支出来，那么无法区分初始硬币态，如果两光子从不同分支出来，那么就可以成功区分初始硬币态。我们通过探测并分析，初始硬币态与相应探测器响应的结果如下表：

表1 初始硬币态与探测器响应结果的对应关系表

经过分析，我们可以区分出两个光子Bell态，再对相应的硬币态进行量子门操作即可得到两个Bell态。

本文中我们利用量子随机行走实现双光子Bell态测量。在物理方案中，通过对光子不同位置的探测，即实现区分出其中两个Bell态，利用现有的实验技术是可行的，与利用偏振分束器(PBS)区分Bell态测量，操作过程有明显的简化，从而极大提高了实验效果。

[1] Dodd P.J.,et al. Disentanglement and decoherence by open system dynamics [J].Phys. Rev. A, 2004, 69：052105.

[2] Cubitt T.S., Verstraete F., Cirac J.I., Entanglement flow in multipartite system [J]. Phys. Rev. A, 2005, 71: 052308.

[3] Ficek Z., Tanas R., Dark periods and revivals of entanglement in a two-qubit system [J]. Phys. Rev. A, 2006, 74: 024304.

[4] Zukowski M., Zeilinger A., Horne M. A., Event-ready-detectors Bell experiment via entanglement Swapping [J]. Phys. Rev. Lett. 1993, 71(26): 4287-4290.

[5] Pan J. W.,Bouwmeester D.,Weinfurter H., andZeilinger A.,Experimental Entanglement Swapping: Entangling Photons That Never Interacted [J]. Phys. Rev. Lett. 1998, 80(28): 3891-3894.

[6] Bouwmeester D.,Pan J. W.,Mattle K.,Eibl M.,Weinfurter H.,Zeilinger A., Experimental quantum teleportation [J]. Nature, 1997, 390:575-579.

[7] Zheng X. J.,Fang M. F.,Cai J. W.,Liao X. P., Teleportation of atomic entangled states with a thermal cavity [J]. Chin. Phys, 2006, 15:492.

[8] Zeng B.,Zhou D.L.,Xu Z.,Sun C.P.,You Encoding a logical qubit into physical qubits [J]. Phys. Rev. A. 2005, 71: 022309.

[9] Kwiat P.G., Klaus Mattle, et al. New High-Intensity Source of Polarization-Entangled Photon Pairs [J]. Phys. Rev. Lett. 1995, 75: 4337.

[10] Zeilinger A., et al. Three-particle entanglements from two entangled pairs [J]. Phys. Rev. Lett. 1997, 78:3031

[11] Klaus Mattle, Harald Weinfurter, et al. Dense Coding in Experimental Quantum Communication [J]. Phys. Rev. Lett. 1996, 76:4656.

[12] Barrett S.D.,Kok P., Nemoto K., et al. Symmetry analyzer for nondestructive Bell-state detection using weak nonlinearities [J]. Phys. Rev. A. 2005, 71:060302.

[13] 陈晓东,肖邵军,顾永建,林秀敏,基于法拉第旋转构造光子Bell态分析器和GHZ态分析器[J].物理学报 2010年08期.

[14] Aharonov Y., Davidovich L., et al. Quantum random walks [J]. Phys. Rev. A. 1993, 48:1687-1690.

[15] Kurzy P., et al. Quantum Walk as a Generalized Measuring Device [J]. Phys. Rev. Lett. 2013, 110:200404.

[16] Bian Z. H., Li J., et al. Realization of Single-Qubit Positive-Operator-Valued Measurement via a One-Dimensional Photonic Quantum Walk [J]. Phys. Rev. Lett. 2015, 114:203602.

Two-photon Bell State Measurement Based on Quantum Walk

LI Xiaoman1,2, LI Dachuang1,2, YANG Ming1, CAO Zhuoliang1,2

(1.SchoolofPhysicsandMaterialScience,AnhuiUniversity,Hefei230039,China;2.SchoolofElectronicsandInformationEngineering,HefeiNormalUniversity,Hefei230601,China)

Quantum entanglement is the central resource in the quantum information and quantum communication. It will be of great significance for development of quantum information to realize the Bell state measurement. In this paper, we propose a physical scheme for two-photon Bell state measurement based on quantum random walk. The system has many advantages, such as better controllability, so the scheme has a certain feasibility and is instructive for the experiments.

quantum walk; Bell states; quantum information; quantum entanglement

2017-01-20

安徽省学术技术带头人及后备人选科研活动经费资助项目(No.2015H052);安徽高校学科(专业)拔尖人才学术资助重点项目(No. gxbjZD2016078)；安徽省高校优秀青年人才支持计划项目；安徽大学研究生创新项目(yqh100012)

李小曼(1991-)，女，安徽大学硕士研究生，主要研究量子信息。

O413.1

A

1674-2273(2017)03-0011-04