三角网格上Lagrange-Thiele型有理插值

陈艳秋，张腊娥

(湖南有色金属职业技术学院，湖南 株洲 412006)



三角网格上Lagrange-Thiele型有理插值

陈艳秋，张腊娥

(湖南有色金属职业技术学院，湖南 株洲 412006)

从Lagrange插值多项式出发,结合Thiele型连分式,构造了三角网格上Lagrange—Thiele型二元有理插值函数,通过定义偏逆差商,建立递推算法,构造的插值函数满足有理插值问题中所给的插值条件,并给出了插值的特征定理,最后给出的数值例子,验证了所给算法的有效性。

三角网格；有理插值；递推算法；特征定理

众所周知，多项式插值结构紧凑，思路清晰，运算简单，在整个数轴上都有任意阶导数，能够进行函数值和微积分的运算。但是,利用多项式插值所求的插值多项式即使通过了所有给定的插值节点，但在其它点上的误差却可能很大，并且插值多项式的次数在七次以上时会出现Runge现象，导致数值不稳定。为了克服多项式插值的缺点，引入了有理分式函数插值，即有理插值，有理插值比多项式插值复杂很多，因为有理插值不但计算更加复杂，而且可能不适定，但是有理插值却为某些非线性问题提供了良好的解决途径。连分式是构造有理插值的常用方法之一，常见的有理插值的构造都是假定有理插值问题有解的条件下给出的。对于矩形网格上的有理插值的研究，已经吸引了许多作者的兴趣，取得了丰硕的成果[1-6]，但考虑到某些给定的数据，如矩形网格是病态的，可能缺失部分数据，此时将不可能在矩形网格上构造一个有理插值函数[7-9]，这也是我们研究三角网格上的有理插值的原因。并且本文巧妙地将Lagrange多项式插值与Thiele型连分式插值结合起来，通过定义偏逆差商，建立递推算法，构造了二元Lagrange—Thiele型理插值函数，给出了插值的特征性质和数值例子。还可以利用Samelson广义逆将本文和插值方法推广到向量值有理插值和矩阵值有理插值的情形。

所谓Lagrange插值，构造多项式：

(1.1)

其中

(1.2)

设平面上的点集由下表给出：

(1.3)

其中xi≠xj,yi≠yj(i≠j)，称之为左下三角网格，记为

(1.4)

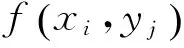
1 三角网格上插值公式的构造

(2.1)

其中

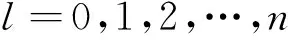
(2.2)

递推算法定义如下：

(2.3)

(2.4)

则由(2.1)～(2.4)可得如下插值定理：

定理1 令aij=φ[xi;y0,y1,…yj]如(2.3)(2.4)式所定义，若所有的aij都存在且不为零，f(x,y)是定义在包含LB的区域D上的二元函数，则由(2.1)、(2.2)定义的R(x,y)为f(x,y)在LB上的Lagrange—Thiele型二元有理插值函数，且满足：R(xi,yj)=f(xi,yj)，(xi,yj)∈LB。

R(xi,yj)=A0(yj)L0(xi)+A1(yj)L1(xi)+…+An(yj)Ln(xi)=Ai(yj)Li(xi)=Ai(yj)

=φ[xi;yj]=f(xi,yj)

故：R(xi,yj)=f(xi,yj)，(xi,yj)∈LB。定理得证。

2 特征定理

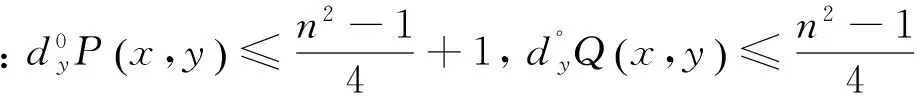
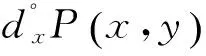
3 数值例子

例1 设f(x,y)在LB上的初始数据如下表：

表1

解 利用混合逆差商的递推算法(2.3)～(2.4)式，列表计算如下：

表2 中间结果1

表3 中间结果2

表4 中间结果3

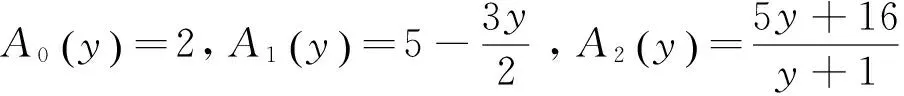
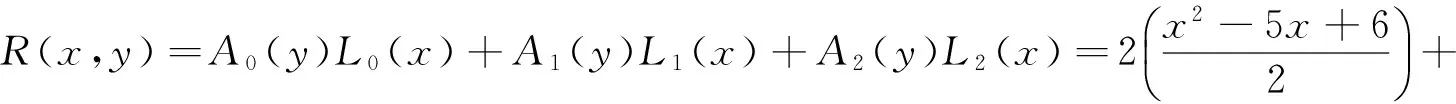
可验证满足插值条件，并且满足特征定理的结论。

5 结束语

本文从Lagrange插值基函数出发，构造了三角网格上的Lagrange—Thiele型二元有理插值函数，对于另外三种三角网格，我们也可以通过定义相应的递推算法，分别构造其上的Lagrange—Thiele型二元有理插值函数。本文插值算法结构简单，使用方便，并且利用Samelson广义逆可以将这种插值算法推广到向量值有理插值和矩阵值有理插值情况。

[1] W.Semaszko.Thiele-type branched continued fractions for two variable functions[J].J.Comput.Appl.Math.9(1983)：137-153.

[2] A.Cuyt,Verdonk B.Multivaite rational interpolation[J].Computing,1985,34：141-161.

[3] Tan Jieqing，Tang Shuo. Composite schemes for multivariate blending rational interpolation[J].J ComputAppl Math,2002,144(1/2)：263-275

[4] 王家正.Stieltjes-Newton型有理插值[J].应用数学与计算数学学报，2006,20(2):15-22

[5] Tan.J ,Q.Bivariate blending rational interpolants.Approx Theory & Its Appl,15(2) (1999) 74-83

[6] Jieqing Tan and Yi Fang.Newton-Thiele’s rational inter Polants，Numevical Algorithms.24(2000)：141-157.

[7] 王家正,梁艳.三角网格上的对称型混合有理插值[J].西安工程大学学报,2008, 22(3): 354-357.

[8] Tan J Q,Song B R,Zhu G Q.Vector valued rational interpolants over triangular grid[J]Computers and Mathematics with Applications,2002，44(10211):1357-1367.

[9] 余小磊，唐烁.三角网格上新的插值公式的构造[J].中国科学技术大学学报，2011，41(6)：504-511.

[10] 檀结庆.连分式理论及其应用[M].北京：科学出版社，2007.

Lagrange-Thiele Type Rational Interpolation Over Triangular Grid

CHEN Yanqiu, ZHANG Lae

(HunanVocationalandTechnicalCollegeofNonferrousMetals,Zhuzhou412006,China)

In this paper, Lagrange-Thiele type bivariate rational interpolation has been constructed over triangular grid, which is based on Lagrange interpolating polynomial and combined with Thiele' continued fractions, by defining partial inverse differences, the recursive algorithms is given, The Lagrange- Thiele rational interpolating function is satisfied with the given interpolating conditions, the characterization theorems of the rational functions is obtained. At last, an example is given to illustrate the effectiveness of the interpolating algorithms.

Triangular grids; rational interpolation; recursive algorithms; characterization theorems

2017-02-06

湖南有色金属职业技术学院院级项目

陈艳秋(1983-)，女，河南商水人，硕士，讲师，研究方向:数值逼近。

O241.3

A

1674-2273(2017)03-0006-03