浅析数学方法在数理金融课程中的应用

杨春志，向伟，李宁

（淮南师范学院金融学院，安徽 淮南 232038）

浅析数学方法在数理金融课程中的应用

杨春志，向伟，李宁

（淮南师范学院金融学院，安徽 淮南 232038）

随着应用型金融人才的社会需求量的不断增加，许多高校开设了数理金融专业课程。为了了解数理金融的数学思想，针对数理金融中的不同案例，运用数学分析、常微分方程和概率论与线性代数的相关定理，求解案例中的相关问题。通过案例分析，有助于掌握数学思想在数理金融中的实际应用，增强数学分析能力。

数理金融；数学方法；案例；分析

引言

数理金融学是数学与金融学相结合产生的一门新兴的学科①张元萍:《数理金融》，北京：中国金融出版社，2004年。孔凡秋，邢永胜：《高校数理金融课程教学方法的改革与研究》，《经济研究导刊》2011年第6期，第290-291页。任嘉嵩：《地方高校金融专业教学中数理分析能力的强化与培养》，《金融教育研究》2014年第27期，第69-71页。顾锋娟，徐爱民：《数理金融专业课程群体系与教学模式构建的思考》，《课程教学》2015年第7期，第112-114页。。在金融交易过程中，度量相关风险和收益这一需求促进了数学在金融活动中的应用。可以说，数理金融将数理概念融入金融分析方法中，使之丰富，并能够揭示金融市场的内在机理，推动金融制度创新。数理金融学的最大特点是通过建模、模型分析来解释和研究金融问题。例如资本资产定价模型，它运用组合理论确定了一条可供投资者选择的有效边界，使得边界上每一点都具有风险水平低、受益较大的特点。而布莱克-斯科尔斯公式是数理金融学又一重大突破，它将期权定价归结为求随机微分方程的解，从而导出与实际相吻合的计算公式，它使得人们可以通过数学分析了解投资时机。布莱克-斯科尔斯的理论不仅在金融领域，在工业界也有应用，例如美国通用汽车公司，就把该理论运用到引入新的生产工艺或新产品的投资决策中，取得很好的效果。随着市场经济的发展，社会对数理金融人才，特别是在货币市场、外汇市场和证券市场等领域的需求量也就越来越多，但目前，许多地方高校金融专业以宏观性和理论性为培养方向，在教学中忽视对学生数理分析能力的培养。所以需要高校数理金融课程对数学思想的进行灌输，要系统、针对性地讲授与数学结合比较紧密的知识点，从而使得数学在数理金融课程中发挥更大的作用；对某些理论性较强的章节，应采取先介绍知识背景，再列举相关的金融案例，使得学生理解金融业务中所需要的方法和技术手段。

一、数理金融的积分思想

在经济管理中，希望生产利润和产出水平尽可能大，而生产成本和环境污染尽可能小，因而需要做出经济函数的最优判断。运用数学分析中的函数极值条件就可解决类似问题。

4

二、数理金融的微分方程思想

微分方程可以求解市场均衡模型的动态平衡点，描述不同经济条件下的价格增长的趋势，也可以估计资本函数，并能根据边际成本函数、边际收入函数估计出总的收益函数。

结论2.1①王高雄，周之铭，朱思铭，王寿松：《常微分方程》(第二版)，北京：高等教育出版社，1983年。：若变量分离方程,其中f(x)g(y)分别是x,y的连续函数，则方程通解为；若一阶非齐线性方程为(x)y+Q(x)，其中P(x),Q(x)分别是x的连续函数，则方程通解为

案例2：假设总体需求为Y，且边际储蓄倾向s和边际资本-产出率k为常数，求可达预计增长的投资函数I。

分析：由于投资的变化率×1=总体需求的变

当生产能力充分利用时总体需求的变化等于资本存量的变化，故

案例3：给定需求函数Q1(t)=5-3P，供给函数Q2=3+4P，若价格的变化率与超额需求成正比，则均衡价格为

分析：假设价格的变化率与超额需求成正比且比值为k(k>0)，则，由定理2.2，得

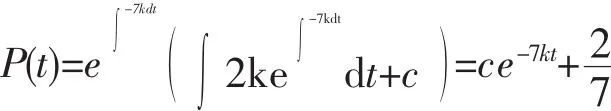
三、数理金融的线代与概率论思想

线性代数作为一个将复杂多元方程简单化求解的数学工具，对分析多种变量相互影响而产生复杂经济现象的经济问题有着重要的作用。而概率论中期望、方差与协方差矩阵法、偏好与期望效用函数思想的应用得以充分体现。

结论3.1②同济大学数学系：《线性代数》(第五版)，北京：高等教育出版社，2007年。：若二元函数f(x,y)在p0(x0,y0)处某邻域具有二阶连续偏导数，记其中fxy=fyx，如果顺序主子式取到极小值，若|H1(P0)|<0，|H2(P0)|> 0，则f(x,y)在P0(x0,y0)取到极大值。

案例4：已知价格函数和总成本函数为：P1=-利润的最大值。

分析：（1）由P1=-3Q1+2Q2+20和P2=5Q1-2.5Q2-5，可知利润函数为

由定理3.2知利润可以取到最大值。

结论3.2①张元萍：《数理金融》，北京：中国金融出版社，2004年。：投资组合选择理论。

不确定性在金融市场无处不在。譬如投资风险，风险就是未来实际收益与预期收益之间的偏离程度在数学上，人们常把股票的未来价格看成一个随机变量或随机过程。由于不同证券、不同时期的股票价格不可比较，便将价格序列转化成百分数表示的可比较的收益率序列。把收益率看成一个随机变量或随机过程，更便于数学处理。费雪曾提出未来资产收益的不确定性可以用概率分布来描述。收益率的概率分布实际上描述了一项投资的风险环境。这样一来，人们可以用收益率R的数学期望E (R)作为未来收益率的点值预测，把R的方D(R)=σ2作为度量未来实际收益率与预期收益率之间偏离程度的数字特征，即用方差(或标准差)来度量投资风险的大小。

投资组合就是对一定数量的风险因素持有量的组合。当将其进行分解后，投资组合的收益就是各种基础资产收益的线性组合，每种资产的权重ω1由最初对该资产投资金额决定。从时间t到t+1期间投资组合的收益为：

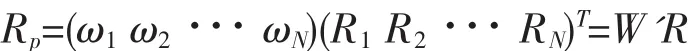
根据概率知识，投资组合的收益期望值可写成E(RP)=μP=ΣNi=1ωiμi

方差可表示为

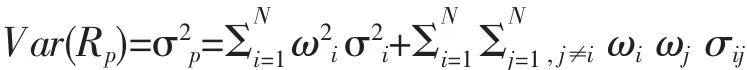
亦可用如下的矩阵表示形式

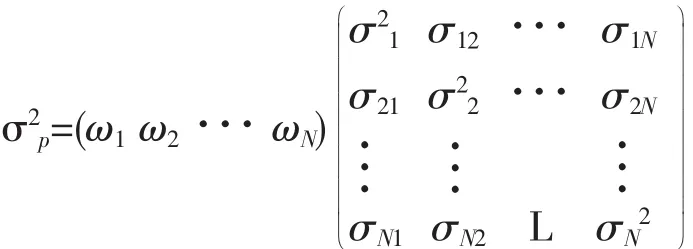
从而投资组合的方差简写为σ2p=W'ΣW。

案例5假设将100万投资于两种资产，风险经理要计算该投资组合的标准差。投资组合的相关数据如下表。

资产1资产2标准差权数相关系数25% 30% 26% 70% 0.7%

分析:首先求出组合的方差协方差矩阵：

四、结束语

当代社会需要应用型金融人才，其竞争优势不仅体现在科研方向和研究领域，也体现在择业方面，所以应用型金融人才必须具备数理金融中的数学分析能力。又数理金融融合了金融学、数学、概率统计学、随机学等多个学科，在人才培养方面既要考虑解决交叉学科的课程内容安排；又要减弱多学科间的界限。而其中数学在数理金融中起到了地基的作用，其重要性不言而喻，如何加强数学分析能力的培养是目前当务之急，需要以人为本，通过结合实际的教学，使得学生逐步养成对金融经济案例具有敏感性的思维方式；同时要适当地改变教学方式，在讲授过程中增强学生参与式学习，鼓励学生表达自己的金融数学思想。还要将学习到的金融数学方法具体应用到实际当中。注重实践运用，特别是分析中国金融市场中的典型案例，运用案例激发学生的兴趣和数学分析能力。

On applying mathematical methods to mathematical finance

YANG Chunzhi,XIANG Wei,LI Ning

As the demand of applied financial talents is continuously increasing,many colleges and universities set up the specialized courses of mathematical finance.In order to understand the mathematical thinking for mathematical finance,we used mathematical analysis,related theorem of ordinary differential equations,probability theory and linear algebra to solve the related problems for different financial cases. Case analysis is helpful to grasp the actual application of mathematical thinking in mathematical finance, and strengthen mathematical analyzing ability.

mathematical finance;mathematical methods;case;analysis

G642

A

1009-9530（2017）03-0120-03

2017-03-01

杨春志（1979-），男，淮南师范学院金融学院讲师，硕士。