多区域交直流混联系统的频率稳定仿真分析

张 欣

(国网黑龙江省电力有限公司电力科学研究院, 哈尔滨 150030)

多区域交直流混联系统的频率稳定仿真分析

张 欣

(国网黑龙江省电力有限公司电力科学研究院, 哈尔滨 150030)

电网的频率是电力系统运行质量和安全情况的重要指标，电力系统调频控制技术对维护电网的安全运行有着至关重要的作用。为了解决交直流互联系统直流输电线路发生直流闭锁故障时影响整个系统频率稳定性问题，建立了交直流混联的三区域系统仿真模型，通过仿真分析了直流系统发生直流闭锁故障时对交流系统频率稳定性的影响。仿真分析结果表明，选择机组不等率要从系统平均不等率、系统稳定性等方面进行综合考虑。调频死区设置越小，系统频率经一次调频恢复至稳定时所用的时间越短。

频率；交直流混联；直流闭锁；稳定性

电网的频率是电力系统最重要的运行参数之一，频率的变化对电力系统安全稳定运行有十分重要的影响[1]。系统的互联虽然增强了系统之间的联系，使其具有了较强的承受有功冲击的能力，但是这样的互联同时也增大了系统可能面临的有功不平衡问题，维持电网频率稳定问题的重要性就更加突出[2]。随着中国西电东送战略的实施，目前电力系统出现了部分特高压直流输电走廊输送功率超过5000 MW。当交直流混联系统发生大机组切除、直流闭锁、联络线切除等故障时，会导致系统频率偏差急剧增大，如2005年华东电网因双极直流闭锁故障导致系统出现约0.5 Hz的频率偏差[3]。此外，大型发电机组对正常运行时频率偏差限制比较严，若系统频率偏差过大，则可能引发系统机组切除等连锁故障，严重时可能发生频率失稳和电网解列[4]。本文对三区域交直流混联系统进行了直流闭锁故障下系统频率稳定性仿真，重点分析了机组不等率和调频死区等参数对系统一次调频性能的影响，得到了系统发生直流闭锁故障时一次调频参数的设置方法，为增强交直流混联电网的频率控制质量提供了理论依据。

1 直流闭锁故障对交直流互联系统的影响

三区域交直流混联电力系统如图1所示，其中区域1和2通过交流和直流联络线共同连接，区域1和3以及区域2和3间分别通过一条交流联络线进行连接。

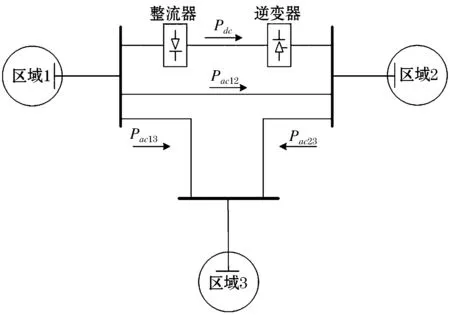
图1 三区域交直流互联系统示意图Fig.1 Schematicdiagram of three-areaAC/DC interconnectedsystem

假设区域1为送端系统，区域2为受端系统，当区域1与区域2之间的直流线路发生直流闭锁故障时，将造成整个系统的潮流大范围转移：一方面会造成区域1与区域2之间的交流联络线传输功率增加，另一方面会导致区域2内产生功率缺额，从而引起频率的大幅度振荡[5]。此时系统运行人员关心的是通过调整哪些参数以及如何调整来减小系统频率的最大偏移值。本文利用MATLAB搭建了三区域仿真系统模型，在此基础上对影响常规机组一次调频性能的机组不等率和调频死区两个参数进行了仿真分析，为增强交直流混联电网的频率控制质量提供理论依据。

2 用于调频分析的数学模型

2.1 调速器的数学模型

调速器是通过改变发电机的蒸汽气流(或进水量)使之满足发电机的转速调节需求，从而达到功率调节的目的。文献[6]详细介绍了调速系统的工作原理，并建立的凝汽式汽轮机转速调节系统的数学模型，如图2所示。在图2中，Ts为油动机的时间常数，To为容积方程的时间常数，Ta为发电机转子时间常数，δ为调节系统的转速调差系数。

2.2 三区域交直流互联系统的多机并列运行数学模型

在研究电网频率的长周期行为时(如一次调频，二次调频)，可以认为电网频率是统一的，各发电机转速均相等，这样的假定实际上是忽略了发电机之间的相对摇摆，认为发电机之间严格地保持同步运行，三区域互联系统的多机并列运行的数学模型如图3所示。在图3中，N1、N2和N3分别为区域

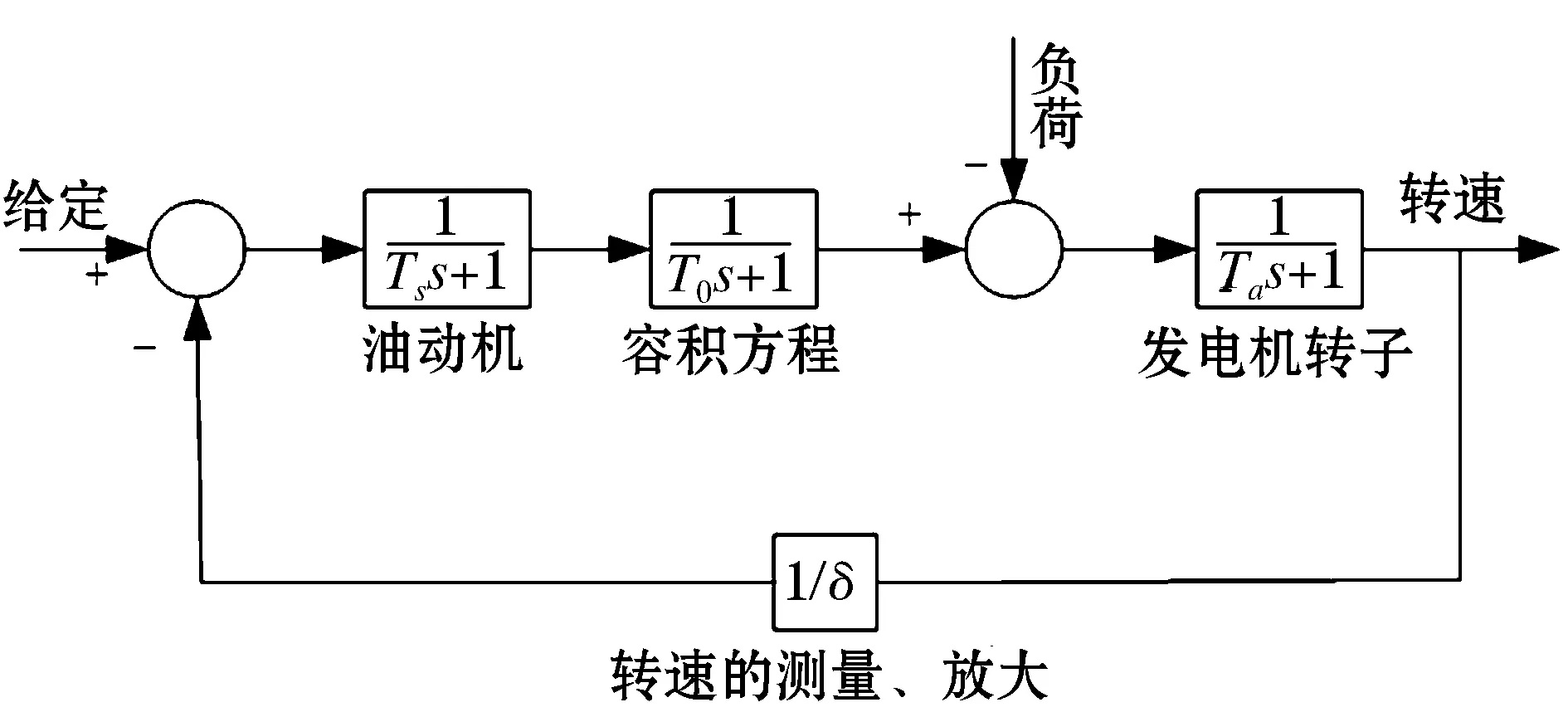
图2 凝汽式汽轮机组转速调节系统数学模型Fig.2 Mathematicalmodelofspeed regulationsystemin condensing steamturbine units

图3 三区域互联系统的多机并列运行的数学模型Fig.3 Mathematical model of multi-machine parallel operation of three-area interconnected system

3 仿真分析

在图3三区域互联电力系统中，每个区域总装机容量为2000 MW，区域1与区域2的直流线路输送功率恒定为400 MW。该系统中包含火电AGC机组、仅参与一次调频的火电机组，其中AGC机组和一次调频机组的发电份额系数分别为0.4和0.6。系统故障条件设置为5 000 s时，区域1与区域2间的直流特高压线路发生直流闭锁故障，系统失去直流提供的所有功率。

3.1 直流闭锁故障条件下机组不等率对一次调频性能的影响

不同装机容量的机组不等率设置情况如表1所示。由表1可知，系统中的机组分为300 MW以下的小型机组，300～600 MW的中型机组以及600 MW以上的大型机组。

表1 不同的机组不等率设置方案Table 2 Variation rate setting proposalsin differentunits

当机组的不等率参数取不同值时，在同一直流闭锁故障下，区域2的频率偏差如图4所示。

由图4可知，当区域1与区域2间的直流特高压线路在5 000 s时发生直流闭锁故障后，系统受到较大的扰动，区域2的频率急剧下降，在一次调频作用下系统频率开始上升。在三种取值方案情况下，系统受扰后频率分别下降了0.25 Hz、0.2 Hz和0.26 Hz，受扰后约10 s频率恢复稳定。经一次调频作用后，系统频率开始恢复，但一次调频是有差调节，稳定后频率偏差分别为0.175 Hz、0.185 Hz和0.14 Hz。如果没有一次调频作用，在系统发生扰动后，系统的频率偏差就会持续下降，最终导致系统失稳。而在一次调频作用下，系统的频率偏差在故障发生后开始恢复，最终形成一个稳态频率偏差。由以上分析可以看出，不等率对一次调频能力有直接的影响，不等率越小，一次调频能力越好，当系统发生直流闭锁故障时，在保证一次调频系统稳定的前提下，应尽可能减小各台机组的不等率，增强系统在直流闭锁故障时的频率稳定性。

3.2 直流闭锁故障条件下调频死区对一次调频性能的影响

同不等率研究时相同，改变仿真模型中各台机组的调频死区的取值范围，保证仿真时机组不等率不变，均为经典参数设置值(表1中方案一)，其他参数设置均相同，系统发生直流闭锁故障时的区域2频率偏差如图5所示。

图4 改变不等率取值时的区域2频率偏差Fig.4 Frequency deviationof Region 2when changingvalue selectionofvariation rate

图5 不同一次调频死区取值时的区域2频率偏差Fig.5 Frequencydeviation of Region2 in valueselections of different primaryfrequency control deadbands

由图5可知，在调频死区取不同值时，系统发生直流闭锁故障后一次调频的响应时间分别为11 s、11.5 s和13.5 s，稳态频率偏差分别为0.185 Hz、0.2015 Hz和0.256 Hz。因此，调频死区越小，一次调频响应时间越短，受扰系统将越快恢复频率稳定。当系统发生直流闭锁故障时，调频死区的减小会使区域电网的一次调频性能更加优化，增强系统的频率稳定性。

4 结 论

本文通过建立多区域仿真模型，在系统发生直流闭锁故障的条件下分析了常规机组不等率及一次调频死区对系统一次调频性能的影响，在此基础上给出了系统发生直流闭锁故障时的一次调频参数设置方法。具体结论如下：

1)发电机组的调速不等率越小，频率稳定后系统的频率偏差越小，一次调频性能越佳，经一次调频作用后的频率恢复效果越好。若单台机组不等率过小，则会导致该机组的不稳定运行，电网中各机组的平均不等率将会影响整个电网的稳定。因此，在选择机组不等率时需从系统平均不等率、系统稳定性等方面进行综合考虑。

2)调频死区的设置会影响系统出现频率偏差后机组何时响应一次调频的问题。通过仿真实验的仿真结果可以看出，调频死区设置越小，系统经一次调频作用后，频率恢复至稳定时所用的时间越短，一次调频发挥的作用就越大。

[1] 郭钰锋. 电网调频过程的动态特性分析[D]. 哈尔滨:哈尔滨工业大学, 2005：1-6. GUO Yufeng. Dynamic characteristics analyses of frequency regulation process in electric power systems[D]. Harbin: Harbin Institute of Technology, 2005: 1-6.

[2] 任丽娜. 互联电网一次调频特性研究[J]. 电工电气, 2013，32(12): 26-27. REN Lina.Primaryfrequencycharacteristicsstudy of interconnectedpower system[J].Electrical& Electronics, 2013,32(12): 26-27.[3] 高翔，高伏英，杨增辉.华东电网因直流故障的频率事故分析[J].电力系统自动化，2006, 30(12):102-107. GAO Xiang, GAO Fuying,YANGZenghui. Frequency accident analysis inEast ChinaGriddueto DC line fault, 2006, 30(12): 102-107.

[4] IEEE Std C37.106 IEEE Guide for Abnormal Frequency Protection for Power Generating Plants[S]. 2003.

[5] 孙宏斌，张伯明，相年德. 配电潮流前推回推法的收敛性研究[J]. 中国电机工程学报，1999，19(7)：26-29. SUN Hongbin, ZHANG Boming, XIANG Niande. Study on convergenceof back/forward sweep distribution power flow[J]. Proceedings of the CSEE, 1999, 19(7):26-29.

[6] 郭钰锋, 徐志强, 于达仁. 汽轮机调节原理[M]. 北京： 机械工业出版社, 2010. GUO Yufeng, XU Zhiqiang, YU Daren. Principle of steam turbine regulation[M].Beijing:China MachinePress, 2010.

(编辑 侯世春)

Simulation analysison frequency stability of multi-area AC/DC hybrid system

ZHANG Xin

(Electric Power Research Institute of State Grid Heilongjiang Electric Power Co.,Ltd., Harbin 150030,China)

Power grid frequency is an important index of power system operation quality and safety while frequency control technology of power system plays a crucial role inmaintaining the safe operation of power grid. When DC block failure occurs on DC transmission line of AC/DC interconnected system, it will cause certain influence to the frequency stability of the whole system. To solve this problem, the simulation model of three-area AC/DC hybrid system is established and the impact on the frequency stability of AC system is analyzed when DC block failure occurson the DC systemthrough simulation. The simulation results show that when choosing variation rate of the unit, the average variationrate, the system stability andother factors should be taken into account comprehensively. The smaller thedead zone is set, the shorter time will it takes to restorethe systemfrequency into stable stage by primary frequency control.

frequency; AC/DC hybrid, DC block; stability

2017-03-13。

张 欣(1964—)，男，高级工程师，从事电力系统、热力系统方面的研究工作。

TM712.3

A

2095-6843(2017)03-0212-04