基于集合经验模态分解的风电功率平抑研究
2017-08-07张礼珏
张 钰, 张礼珏
(东北电力大学 电气工程学院,吉林 吉林 132012)
基于集合经验模态分解的风电功率平抑研究
张 钰, 张礼珏
(东北电力大学 电气工程学院,吉林 吉林 132012)
为减少风电功率波动,提高风电并网可靠性,提出一种基于集合经验模态分解(ensemble empirical mode decomposition,EEMD)的电池储能平抑风电功率方法。对于风电功率高频分量,采用荷电状态(state of charge,SOC)自适应调整移动步长的移动平均法控制算法对其平滑处理,同时避免电池过充过放。算例仿真结果表明,该方法可有效降低功率波动,从而提高系统运行稳定性。
集合经验模态分解;风力发电;储能系统;平抑功率;风电波动率
近年来,世界各地对能源需求量逐步增加,风能的利用及在电网中渗透率经历了前所未有的增长。与此同时,风电功率输出的间歇波动性对电网稳定运行带来了许多挑战[1-2]。国家对于风电功率波动偏离范围进行了较为严格的限制[3],因此,能否应用一个有效、经济的方法减少风电不稳定输出对电网的影响是关系风电发展的关键。
文献[4-5]分别采用桨距角控制和风力机转子惯性管理的方法。然而这两种基于风电机组自身调节的方法以牺牲最大功率为前提,平抑控制能力受到机组自身制约,总体来说是不经济的。随着储能技术的发展,有学者提出在风电场中配置一定容量的储能设备,有效降低风电机组输出功率的波动性,从而提高系统的稳定性[6]。文献[7]基于风电功率预测精度及储能能量约束,根据平滑需求提出了平抑风电功率波动的储能系统运行控制策略,但该方法没有考虑到荷电状态,经常出现过冲过放,会影响电池性能。文献[8]在一阶低通滤波的基础上加入储能荷电状态反馈和有功功率限幅环节,通过对逆变器控制,有效避免了电池的电压偏离运行。文献[9]为改善风储混合系统的性能,提出应用电池荷电状态的模糊逻辑控制方法,使电池SOC保持在预期的范围内,并减少储能系统的容量。为降低风电调度风险、提高风电并网渗透率,文献[10]提出利用储能平抑风电预测功率误差区间的方法,并通过对几种评价指标评估验证其有效性。
本文通过对风电功率波动特性分析,提出应用集合模态分解法拆解风功率,将其分为高、低频功率。采用SOC控制移动步长的移动平均法平抑高频功率,考虑到低频功率较为平滑,所以对其不做平抑。通过该控制策略可解决电池的过充过放,对风电功率波动也起到了显著的效果。
1 风电功率的分解
1.1 集合经验模态分解
集合经验模态分解是对经验模态分解(EMD)的一种改进,即对于分解出的固有模态分量中可能包含了不止一种模态的缺点进行优化。在经验模态分解之前加入不同幅值的高斯白噪声信号,根据高斯白噪声序列可以抵消的原理,使其接近真实序列。将分解后得到的固有模态分量(IMF)的均值看作是真实分量。每个固有模态分量需要同时满足以下两种情况:1)信号的零点数和极值点数至多相差一个;2)局部极值点定义的包络线均值为零。集合经验模态可以把信号分解成若干个不同频率不同幅值的IMF分量。
EEMD分解的具体步骤如下:
1)向原始数据序列x(t)中加入随机高斯白噪声序nj(t),可得加入噪声序列后的序列为
xj(t)=x(t)+knj(t)j=1,2…,M
式中:k为白噪声的幅值,j为添加噪声次数。
2)按照常规EMD步骤对xj(t)分解,得到多个IMF分量和一个剩余分量:
式中:ci,j和rn,j分别为第j次分解得到的第i个IMF分量和第j次分解的余量。
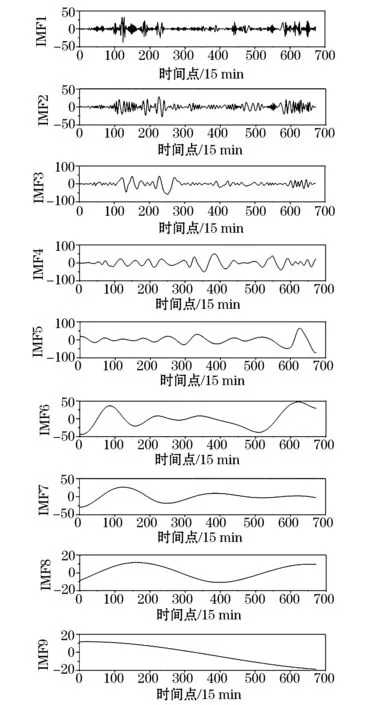
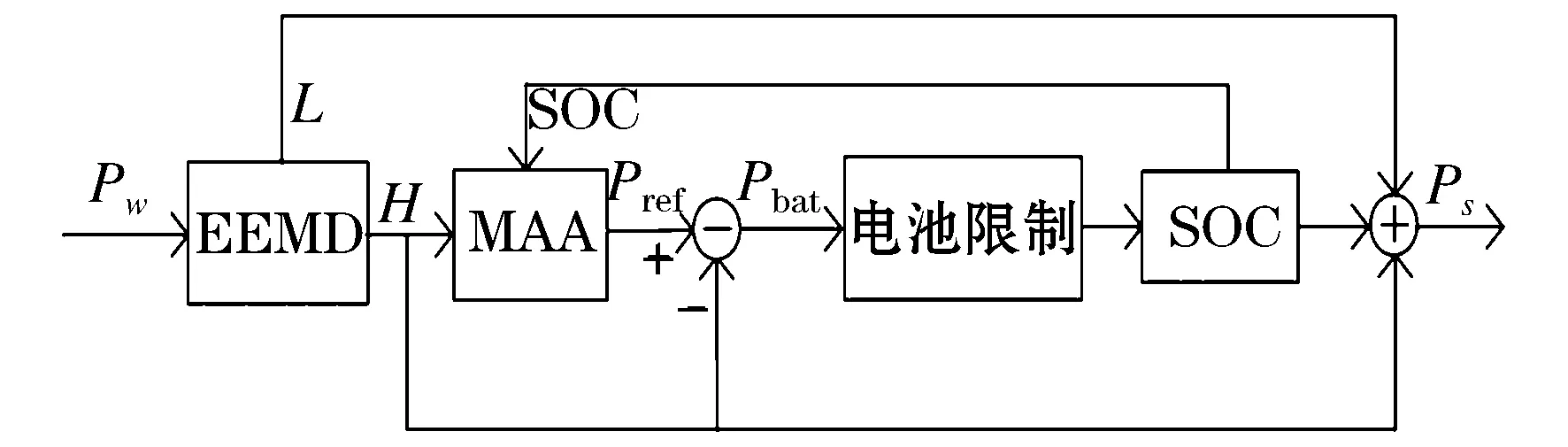
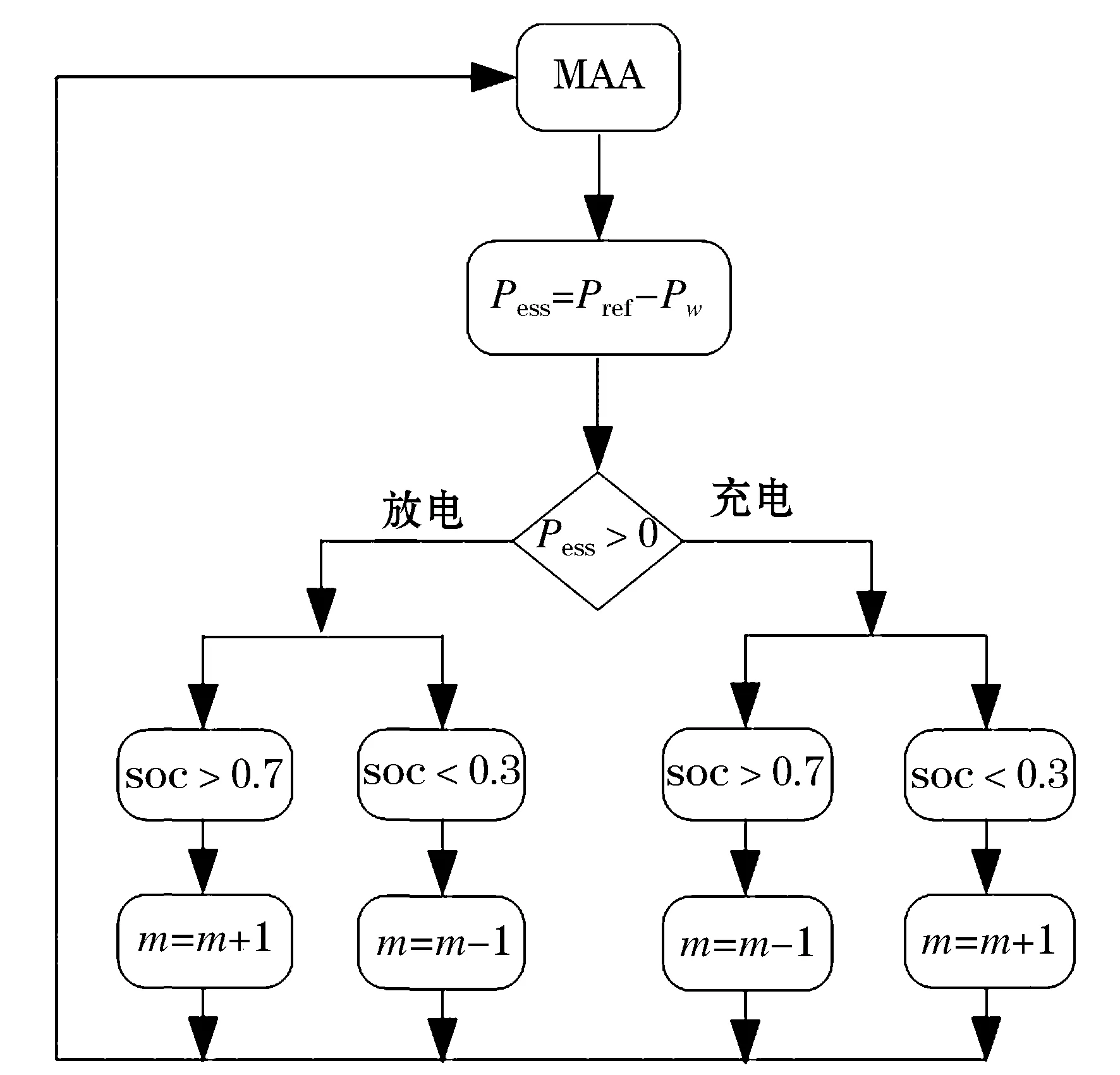
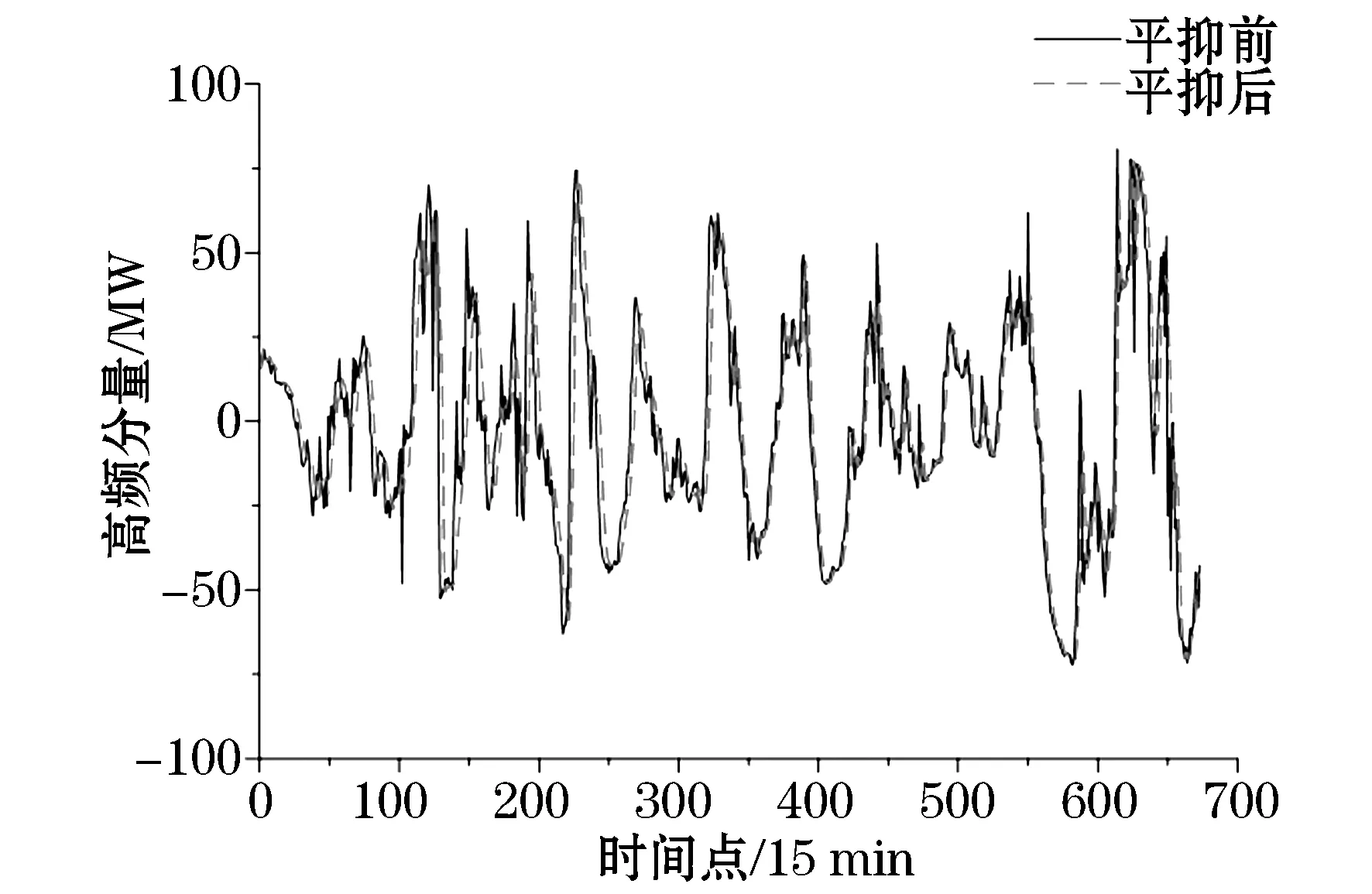
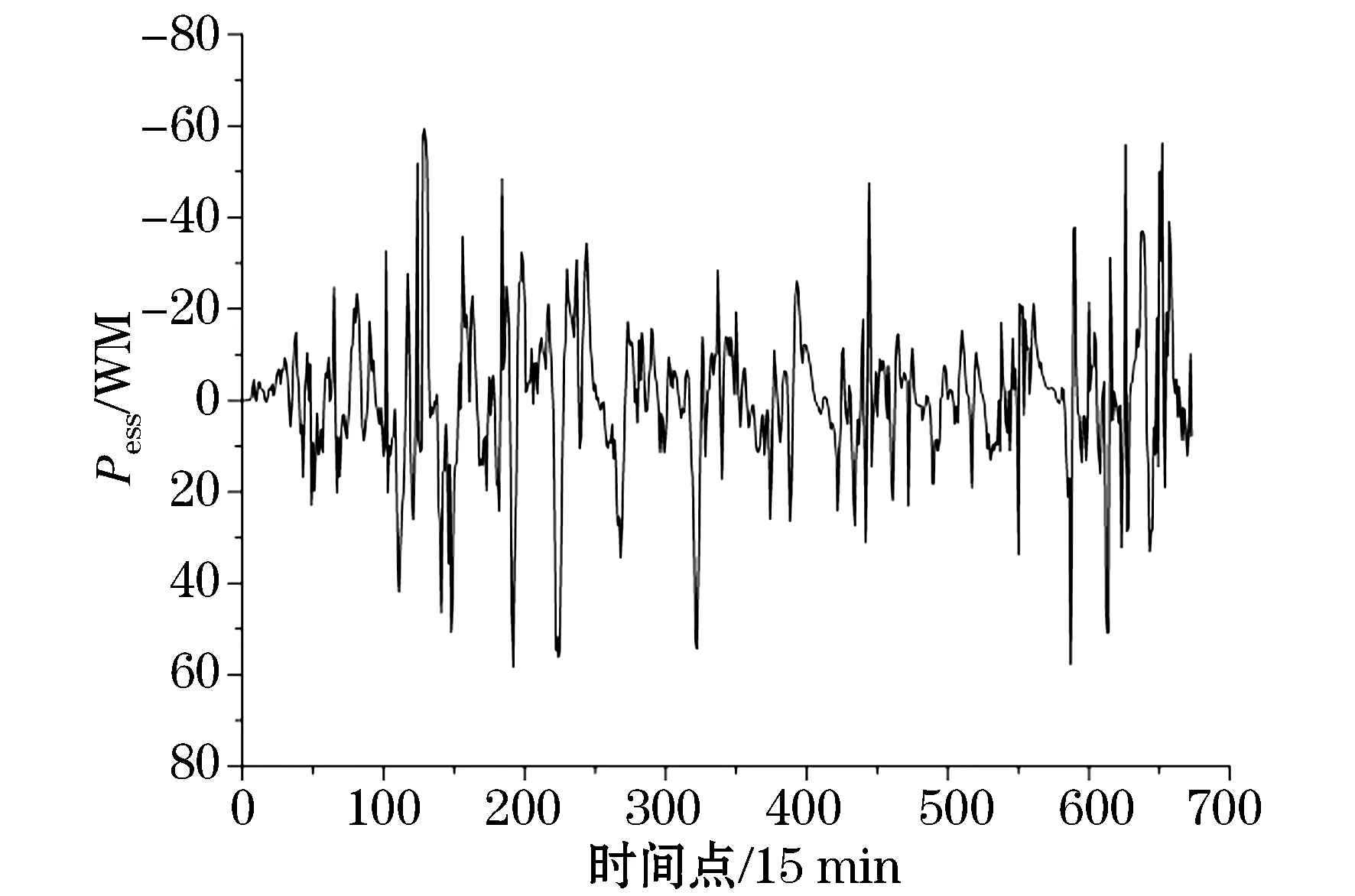
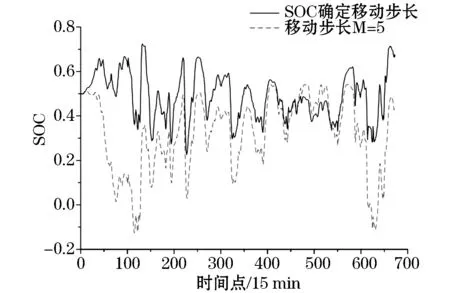
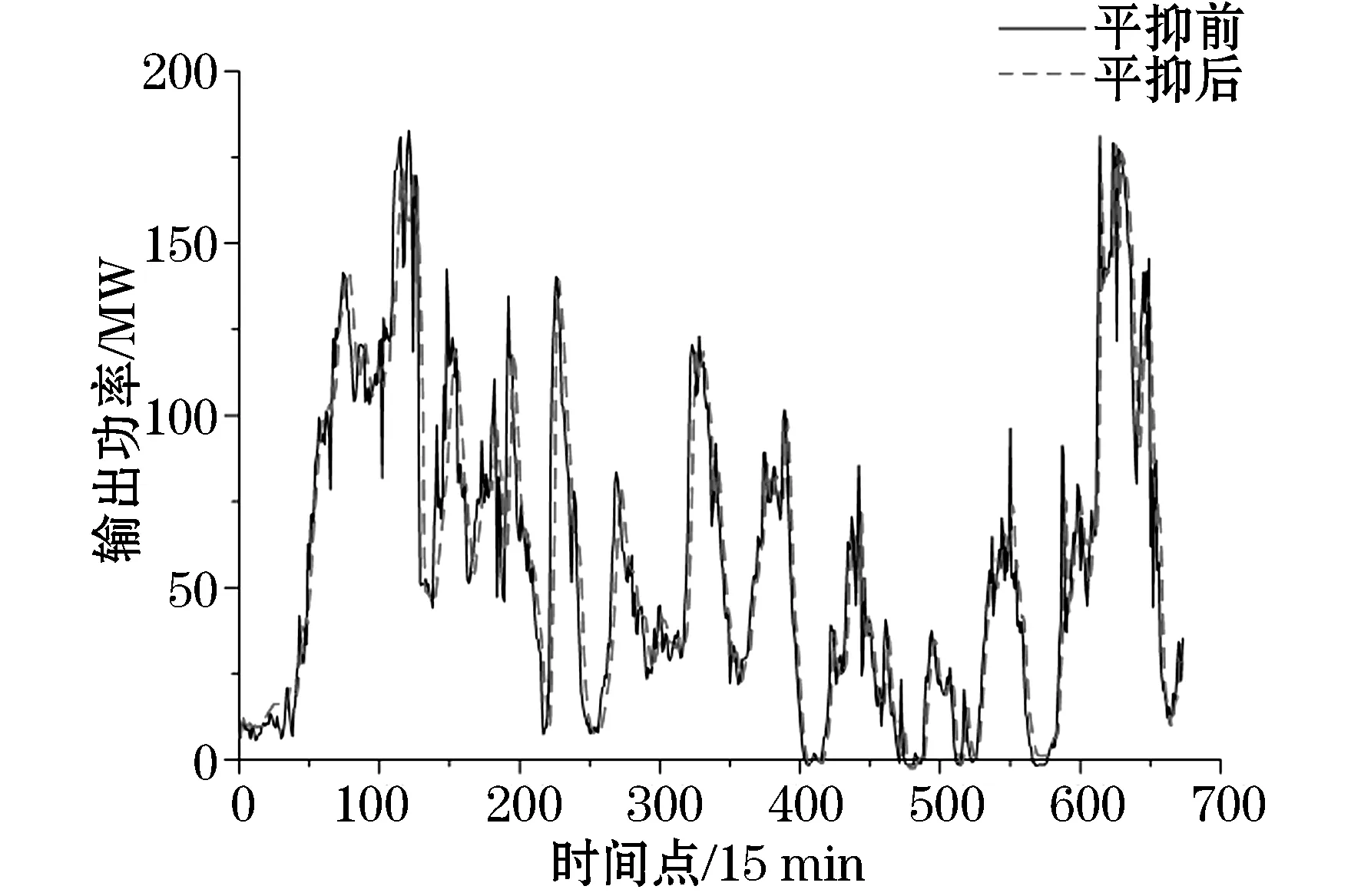
3)若j 4)对经过M次EMD分解的各分量计算均值: 1.2 风电功率的集合经验模态分解 EEMD方法理论上可以应用于分解任何类型的时间序列信号,并具有处理非平稳和非线性数据的优势。图1为采样间隔为15 min的某风电场数据,采样点共673个。 图2为风电功率经EEMD分解后的各频分量。可以看出:分解得到的子序列频率是从高到低依次排列的,振幅越低频率越低。IMF1为瞬时频率最高分量,波动最为明显;IMF9为瞬时频率最低分量,波动相对来说最为平缓。 图1 风电场输出功率曲线Fig.1 Wind farm output power curve 图2 风电功率分解曲线Fig.2 Wind power decomposition curve 对于高频分量由于其波动量较大采用平抑控制算法平滑处理,之后与原低频分量叠加得到新的风电功率期望值。 2.1 风储系统模型 本文提出的风储系统包括风电机组、储能装置、能量调度单元(EMS),如图3所示,其中Ps为经储能平抑后的风储并网功率。 图3 风储系统为结构图Fig.3 Wind storage system structure diagram 能量调度单元通过采集风电功率及储能系统状态,对该系统发出功率期望值Pref,期望值与风电机组输出功率Pw的差值为储能需要提供的功率Pess。在满足储能系统自身约束的同时,储能完成对风电功率波动的平滑。 2.2 储能系统平抑风电功率 对过去某一段时间的数据取算数平均值作为下一时刻的期望量,这种方法就是移动平均法(Moving Average Algorithm,MAA),即 (1) 该方法计算量较小,迭代过程中可快速、准确地处理数据。由式(1)可以看出,步长M决定了该方法的平抑效果,一般情况下M取值范围为2~100。M值越小,对于数据处理的精度越高,适合处理有突变和阶跃性质的数据,能较好地给出曲线细节,但平滑度差;M值越大,数据平滑效果越明显,适合处理变化趋势单一,以及较多随机变量的数据,但是可能造成结果与原始数据的偏离。所以要根据需求合理选择步长。 图4为储能平抑风电功率波动控制策略框图。风电功率由EEMD分解后,高频风电分量随着时间变化存在较大的波动,应用上述移动平均法进行平滑计算下一时刻风电输出功率的预期值,预期值与实际高频分量的差值即为应用储能平抑部分。考虑到储能自身运行限制,根据电池储能装置荷电状态对移动平均法中移动步长进行优化控制。最后,将风电功率高频量的平滑值与低频值做和,便可得到经该策略输出的总功率平滑值Ps。 图4 控制框图Fig.4 Control block diagram 电池储能系统的荷电状态是很重要的参数,表征着剩余电荷量在储能装置总容量的占比,表达式为 SOC(t)=SOC(t-Δt)+PbatΔt/Ebat 式中:Ebat为电池储能的额定容量;△t为采样间隔;SOC初始值设为0.5,运行限制不大于0.8或不小于0.2。本文将SOC划分为三个等级分别为高、中、低。 当储能SOC处于较高级别且需要充电时,需要减小式(1)中的移动步长和储能充电量,以免出现过充或满充;当需要放电时,需要增大移动步长,从而增加储能对于风电的平抑效果,且满足自身的特性约束。图5为移动步长与SOC的关系框图。 图5 移动步长与SOC的关系Fig.5 Relationship between shift step length and SOC 本文数据采集于某装机容量为200 MW的风电场,采样间隔为15 min,采样点为673个。储能电池的最大输出功率和容量分别为60 MW和60 MW·h。 风电功率采用EEMD分解为9个不同频率的分量,如图2所示。IMF1~IMF5分量中波幅较大,为高频分量,IMF6~IMF9中波幅较小,为低频分量。将高频分量拟合得到高频分量曲线,由于低频分量较为平缓,该曲线能反映出该组风电数据的波动,可以作为功率平抑目标。经过本文所提出的SOC确定移动步长的变步长移动平均法对高频分量进行平抑处理,考虑储能容量和平抑效果约束,初始移动步长M设为5。高频分量平抑结果如图6所示。 图6 高频分量平抑结果Fig.6 High frequency component smoothing result 图7 储能输出功率Fig.7 Energy storage output power 储能输出功率如图7所示。风电功率高频期望值Pref与风电功率高频实际值Pw之差即为储能输出功率指令值Pess。若Pess大于0,储能系统充电;若Pess小于0,储能系统放电。充放电模式下根据SOC不同,单独调整移动步长。图8为移动步长变化曲线。 根据控制策略,当SOC介于0.3~0.7之间时,M不发生改变,减少控制策略复杂性和计算。当SOC小于0.3或大于0.7时,根据充放电特性,储能系统SOC决定移动步长的增减。图9为采用本文提出的控制策略与传统固定步长平抑方法的储能电池SOC对比,显然固定步长方法电池储能SOC波动量相对较大,并且出现了过放现象,对于储能系统的稳定和寿命都有所影响。若改变这种问题需要提供更大的储能容量配置,投资成本和运行成本也会增大。根据充放电状态不同,独立自适应地改变移动步长,使得SOC较为稳定且避免了过冲过放现象,从而提高了储能系统经济性,达到平抑目的。 图8 移动步长变化Fig.8 Shift step length change 图9 两种控制策略下储能电池SOC对比Fig.9 Comparison of energy storage battery SOC under two control strategies 将高频分量平抑结果与未作平抑的低频分量叠加,如图10所示。在保证风电功率原有运行方法的同时,对于波动量较大的功率值有较好的平滑。通过分析输出功率波动率便可验证该控制算法的有效性,平抑前后波动率对比如图11所示。 式中:PN为风电场的额定容量;P(t)为t时刻风电功率输出;F.Rwind为风电功率波动率。 应用本文提出控制算法后,风电功率波动率占比介于-5%~5%,由77.6%提高到90.6%,同时,功率输出波动较大的部分明显减少,如图11所示。 图10 平抑结果Fig.10 Smoothing result 图11 波动率分析Fig.11 Volatility analysis 为降低风电并网波动,本文提出一种利用储能平抑风电功率波动的方法。该方法应用EEMD将风电功率分解,利用储能平抑高频分量,根据电池SOC自适应调节移动步长。算例分析表明,该方法对风电功率平滑、稳定电池SOC效果明显,并有效避免了电池的过充过放。 [1] 林卫星, 文劲宇, 艾小猛, 等. 风电功率波动特性的概率分布研究[J]. 中国电机工程学报, 2012, 32(1): 38-46. LIN Weixing, WEN Jinyu, AI Xiaomeng, et al. Probability density function of wind power variations[J]. Proceedings of the CSEE, 2012, 32(1): 38-46. [2] 薛禹胜, 雷兴, 薛峰, 等. 关于风电不确定性对电力系统影响的评述[J]. 中国电机工程学报, 2014, 34(29): 5029-5040. XUE Yusheng, LEI Xing, XUE Feng, et al. A review on impacts of wind power uncertainties on power systems[J]. Proceedings of the CSEE, 2014, 34(29): 5029-5040. [3] GB/T19963-2011 风电场接入电力系统技术规定[S].北京: 中国标准出版社, 2012. [4] UEHARA A, PRATAP A, GOYA T, et al. A coordinated control method to smooth wind power fluctuations of a PMSG-based WECS[J].IEEE Transactions on Energy Conversion, 2011, 26(2): 550-558. [5] ABEDINI A, MANDIC G, NASIRI A. Wind power smoothing using rotor inertia aimed at reducing grid susceptibility[J]. International Journal of Power Electronics, 2008, 1(2): 227-247. [6] ZHANG W L, QIU M, LAI X K. Application of energy storage technologies in power grids [J]. Power System Technology, 2008, 32(7):4. [7] 李蓓, 郭剑波. 平抑风电功率的电池储能系统控制策略[J]. 电网技术, 2012, 36(8): 39-43. LI Bei,GUO Jianbo. A control strategy for battery energy storage system to level wind power output[J]. Power System Technology, 2012, 36(8): 39-43. [8] 谢俊文, 陆继明, 毛承雄, 等. 基于变平滑时间常数的电池储能系统优化控制方法[J]. 电力系统自动化, 2013, 37(1): 96-102. XIE Junwen, LU Jiming, MAO Chengxiong, et al. Optimal control of battery energy storage system based on variable smoothing time constant[J]. Automation of Electric Power Systems, 2013, 37(1):96-102. [9] LI X, HUI D, WU L, et al. Control strategy of battery state of charge for wind/battery hybrid power system[C]//IEEE International Symposium on Industrial Electronics (ISIE). IEEE, 2010: 2723-2726. [10] 严干贵, 冯凯翔, 刘嘉, 等. 基于风电功率预测误差区间的储能系统控制策略[J]. 储能科学与技术, 2015, 4(4): 388-393. YAN Gangui,FENG Kaixiang,LIU Jia. et al. A control strategy for energy storage system based on wind power prediction error interval[J]. Energy Storage Science and Technology, 2015, 4(4): 388-393. (编辑 侯世春) Research on wind power smoothing based on ensemble empirical mode decomposition (EEMD) ZHANG Yu, ZHANG Lijue (College of Electrical Engineering, Northeast Dianli University, Jilin 132012, China) In order to reduce wind power wave and improve the reliability of wind power integration, wind power smoothing method of a kind of battery energy storage is proposed based on ensemble empirical mode decomposition (EEMD). As to the wind power high frequency component, the moving average method, a kind of control algorithm that can make an adaptive adjustment to shift step length in a state of charge (SOC) is used to process smoothly and to avoid the battery overcharge and discharge. The results of example simulation show that this method can effectively reduce power fluctuations, thereby improving the system’s running stability. ensemble empirical mode decomposition (EEMD); wind power; energy storage system; smoothing power; wind power volatility 2016-12-28; 2017-03-22。 张 钰(1992—),女,硕士研究生,研究方向为风电并网控制。 TK81 A 2095-6843(2017)03-0199-05

2 基于EEMD的储能平抑风电功率

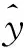
3 算例分析

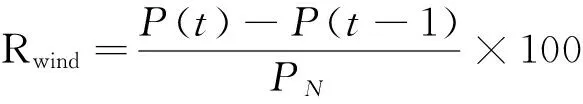

4 结 论
