基于联合引力度扩展的加权网络重叠社区划分算法

孙延维， 雷建军， 杨进才

(1.华中师范大学 教育信息技术学院， 武汉 430079； 2.湖北第二师范学院 计算机学院， 湖北 武汉 430205)

基于联合引力度扩展的加权网络重叠社区划分算法

孙延维1，2， 雷建军2， 杨进才1*

(1.华中师范大学 教育信息技术学院， 武汉 430079； 2.湖北第二师范学院 计算机学院， 湖北 武汉 430205)

基于引力度扩展的重叠社区发现算法(GDE)，主要用于挖掘无权社交网络的重叠社区结构.真实社区更多是具有加权属性的，本文根据 GDE 算法的种子策略思想，并依据加权网络的特征，以网络节点的度与强度来综合确定重叠社区的中心节点，提出基于联合引力度扩展的加权网络重叠社区划分算法(UGDE).算法的实验检测结果表明：该算法对划分加权网络中的重叠社区具有可行性与有效性.

重叠社区； 联合度； 联合引力度； 社区划分； 加权网络

复杂网络解析[1-3]的一个重要研究问题就是社区结构，而重叠社区结构更能体现现实世界里人们可以自由加入多个团体的实际情况.因此，发现复杂网络的重叠社区结构就成为社区研究的热点，且这一研究的突破将会对探究人类社会交往方式的进展起到里程碑的推动作用.

如今，已有计算机科学、统计学、应用数学、统计物理领域的科学工作者们在发现复杂网络重叠社区结构上做了大量的科研工作，并产生了很多重叠社区发现方法.其中有基于适配标签传播的ALPA算法[4]，使用链路空间变换的LinkSCAN算法[5]，基于边界非负矩阵三角分解的(BNMTF)方法[6]，边密度聚类算法 (LDC)[7]，基于马尔科夫随机游走控制策略的UEOC方法[8]，通过多目标进化的MEA_CDP算法[9]等.

以上的方法都是针对无权网络的，而真实社会中的个体往往是带有很多社会交际信息的，这种信息可由复杂网络的边权重体现出来，即加权网络更能确切的表达人们的日常活动信息.因此，研究加权网络的重叠社区结构具有更大的社会价值.目前，用于挖掘加权复杂网络重叠社区结构的算法较少，本文运用GDE算法[10]的种子策略，并根据加权网络的特性，用节点的强度与度来联合肯定重叠社区的中心节点，由此提出基于联合引力度扩展的加权网络重叠社区划分算法(UGDE).

1相关概念介绍

1.1加权网络节点的联合度

在社交加权网络中，权值一般代表了节点联系的密切度，节点间边的权重值越大，说明两个节点间的日常往来越亲密，反之，交往则越稀少.而在加权网络中，根据节点间边的权值来判断节点之间的相互影响力度是无可厚非的，但是节点与多少个节点之间有直接交往关系，也是不容忽略的.因此，衡量加权网络中任意节点对网络中其他节点的直接影响力的大小不能只单一从权值判断，而应该将节点的度与节点的强度联合考虑.

设定加权网络Gw(Vw，Ew)，其中网络节点集合的数学表示为Vw，网络边集合的数学表示为Ew.设定任意节点a∈Vw，节点a的联合度定义参考文献[11]，将其定义为：

(1)

式中，ka是节点a的度，sa是节点a的强度，β是一个为正数的调节参数，它将节点a的度与a的强度联合了起来，且β∈[0，1].

1.2加权网络节点的联合隶属度

设定一个加权网络Gw(Vw，Ew)，以及Gw中的一个重叠社区cw∈Cw，Cw是Gw的一个重叠社团划分，且∀a∈Vw，则将节点a对重叠社区cw的联合隶属度Bw(a，cw)定义为：

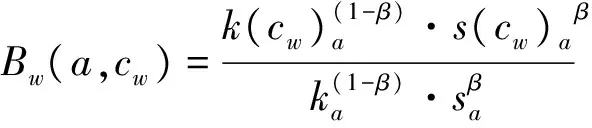
(2)

其中，k(cw)a是节点a对重叠社区cw的连接度，s(cw)a是节点a对重叠社区cw的连接强度.

1.3加权网络节点间的最短路径

一个无向、无权网络G(V，E)，及∀a，b∈V，则节点u与节点v之间的最短路径[11]定义为：

d(a，b)=min(Aai+…+Aib)，i∈V,

(3)

其中，i表示a可达b通过的所有中间节点，Aai是网络G的邻接矩阵A里的元素.

在加权社会网络中，节点间边的权重值一般表示的是节点间讯息交流的亲近程度，而不是节点间的路径长度，从理论意义上讲，当权值越大，节点间消息的互动应该更加频繁，通过彼此影响感染网络中的其他节点的可能性更高，他们的理论路径应该更短.一个加权网络Gw(Vw，Ew)，及∀a，p∈Vw，则将节点a与节点p之间的加权最短路径[11]定义为：

(4)

图1 简单的加权网络图Fig.1 A simple weighted network

1.4加权网络节点的联合引力度

一个加权网络Gw(Vw，Ew)，∀a∈Vw，则节点a的联合引力度定义为：

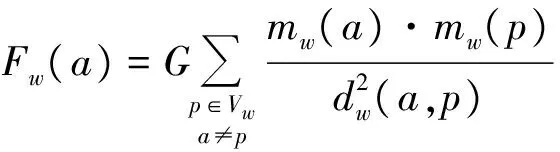
(5)

其中，mw(a)、mw(p) 分别是节点a、节点b的加权质量，由文献[10]可知，mw(a)=Ua，mw(p)=Up.

2基于联合引力度扩展的加权网络重叠社区划分算法

加权网络Gw(Vw，Ew)，对加权网络节点的归属状态进行初始化，给∀a∈Vw一个原始划分标记“N”，即节点a未被指定到重叠社区里，当节点a被分派到某个重叠社区里时，将其节点的划分标记更新为“J”.

2.1算法描述

1) 挖掘中心社区

步骤1：∀a∈Vw，且a的划分标记是‘N’，由式(1)计算出节点a的联合度，式(4)计算出节点a与其他节点间的加权最短路径，再由式(5)计算出节点a的联合引力度；

步骤2∶Gw中联合引力度最大的节点被指定为一个重叠社区的种子节点s；

步骤3：将与种子s是邻居关系的节点集记为VL，∀b∈VL，且b的社区归属状态为‘N’，则将b加入种子s的社区里，最终，此类节点就和s构成了中心社区ch，ch的节点集记作Vh；

步骤4：∀a∈Vh，计算出节点a的Bw(a，ch)值，若BT>Bw(a，ch)(BT是重叠社区联合隶属度的门限值)，则在Vh中减除节点a；

步骤5：回溯至第4步骤，直至∀a∈Vh，都满足BT≤Bw(a，ch)，此时中心社区ch被明确.

2) 中心社区的扩展

步骤1：将社区ch的邻舍节点集记作VJ，∀b∈VJ，计算其Bw(b，ch)值；

步骤2：设定一个节点集VF=∅，∀b∈VJ，若BT≤Bw(b，ch)，将节点b加入到VF中，即VF=VF+{b}；

步骤3：若VF≠∅，则社团ch里就增加VF中的节点集，这样就组成了一个具有更多成员的社区ch，回溯至第1步骤；

步骤4：若VF=∅，一个加权网络重叠社区ch就被确定与发现.

2.2UGDE算法流程

图2是基于联合引力度扩展的加权网络重叠社区划分算法的流程图，该图诠释了UGDE算法怎样划分出加权网络中的一个重叠社区，并直到整个加权网络的重叠社区结构被发现.

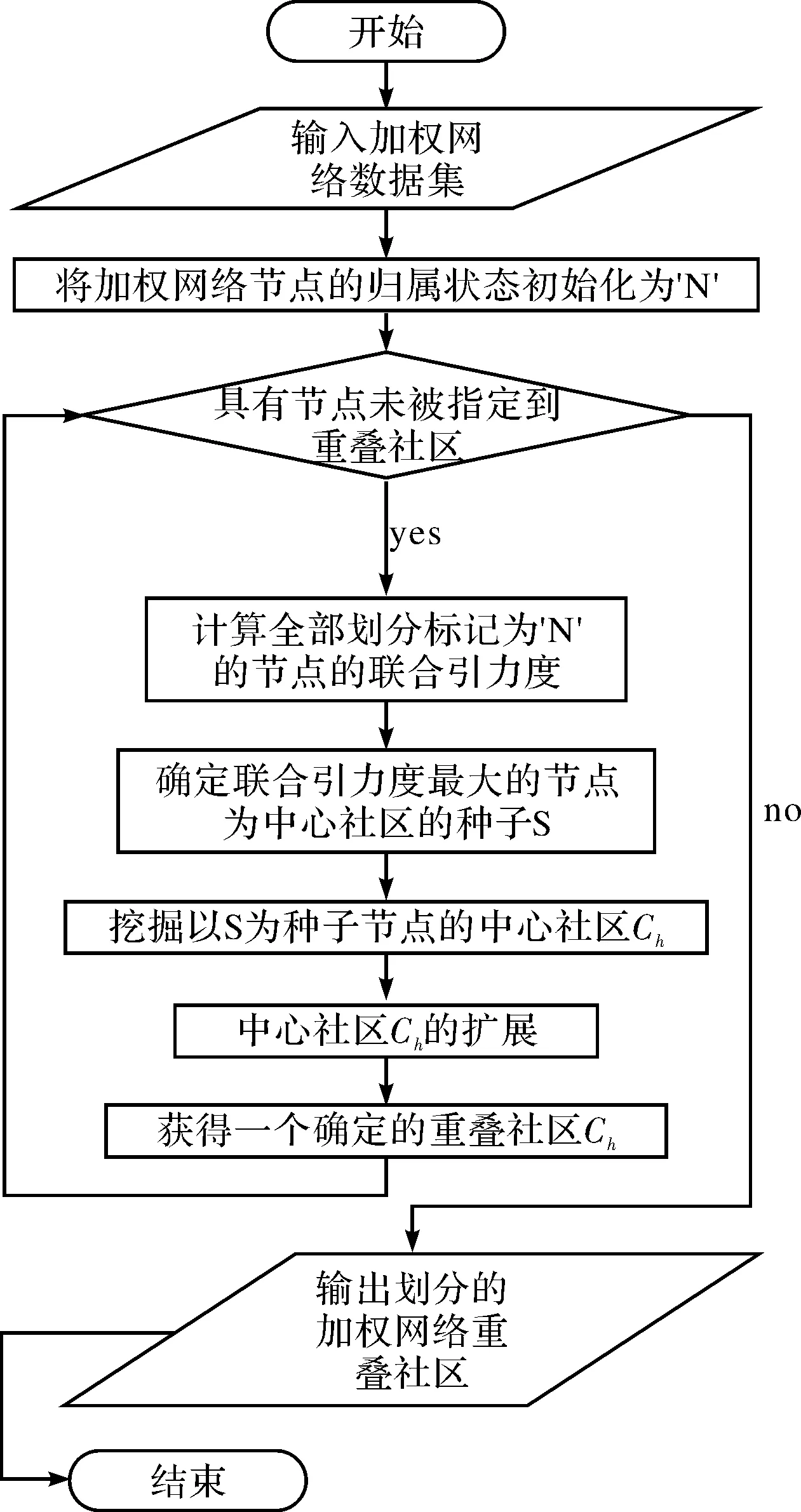
图2 UGDE算法的流程图Fig.2 Illustration of the algorithm process for UGDE

3实验分析

将基于联合引力度扩展的加权网络重叠社区划分算法在实际的加权网络上进行实验，以检测该算法的有效性与可行性.本文还将该算法与EM-BOAD算法[12]、LOC算法[13]做了执行效率与重叠社区结构划分质量上的比较.

3.1算法执行效率的理论分析与比较

本文的UGDE算法计算加权网络任意节点对之间的带权最短路径长度的时间复杂度是O(n3)，导致算法执行性能较差，因而UGDE算法的时间复杂度在最优情况，即网络中只存在一个社区时，是O(n3)；而最差情况，即每个节点自成一个社区时，是O(n4)，n是网络的节点个数.EM-BOAD算法的时间复杂度最优情况是O(n)，最差情况是O(n2).LOC算法的时间复杂度最优情况是O(n2)，最差情况是O(n3).

从以上分析可知，UGDE算法的时间复杂度是三者中最高的.因此，本文借鉴六度分割理论[14]的思想(地球上任意两个人之间要产生联系，平均中间只需要通过5个人就可以了)对该算法进行优化.文中将网络中任意节点的全局加权引力度优化为计算以该节点为起始节点，并通过5个节点内可达的全部节点的局部加权引力度.则UGDE算法的时间复杂度在最好情况，就变为O(n2)；而最差情况则变为O(n3).

3.2加权网络重叠社区结构质量函数模块度

当在不知晓一个网络的实际社区结构的情形下，通常采用模块度函数来判断实验环境下获得的社区结构的质量如何.本文采用文献[13]中的模块度Qo，该指标是专门针对评估加权网络重叠社区结构质量的优劣而提出的模块度函数.Qo的定义为：

(6)

其中,w表示加权网络的连接边的权重总和，wab表示加权矩阵W的元素,

(7)

3.3实际加权网络数据集

本文实验的实际数据集有Zachary’skarateclub[15]，lesmis[16]，netscience[17]，astro-ph.其中lesmis是法国大作家维克多·雨果在1862年发表的小说《悲惨世界》中人物之间的关系网络，该网络含有77个人物节点，254条带权人物关系边，边上的权值表示了某对人物在小说同一章节出现的次数.netscience是科学家在网络理论与实验研究这一领域的合作关系网络，其中有1 600个研究者节点，2 743条赋权关系边，边权重表明某两位学者共同合作研究的频率大小.astro-ph是学者在天体物理学这一领域的协作关系网络.

3.3.1参数β取值讨论 本文算法中的正数调节参数β值的设置参考文献[11]，将β的值定为0.5，重叠社区归属阀值BT仍采用文献[10]中的取值.

为了验证β取0.5时，本文算法是否能得到最优结果，我们在实验中做了检验，且β的增加步长设置为0.1，其测试结果如图3所示.

图3为参数β与加权网络重叠社区结构质量评价指标Qo之间的关系图.解析图3可知，当β为0.5时，Qo值最大，此时UGDE算法在Karate、lesmis、netscience网络上获得的加权重叠社区结构的质量最佳，结构性最强.因此，β应该设定为0.5.

图3 β与Qo的关系图Fig.3 The relationship between β and weighted modularity Qo

3.3.2算法对karateclub的重叠社区划分 由于karateclub只有34个成员节点，78条有权关系边，它的网络规模就比较小，可显而易见的从网络可视化角度来清楚的分析其重叠社区划分结果.karateclub的带权重叠社区结构如图4.图4为Zachary’skarateclub的加权重叠社区划分结构图，其中的(1)、(2)子图分别是阀门参数BT=0.5与BT=0.4的重叠社区结构图.由图中可知，本文算法将karate club划分成2个加权重叠社区，两个子图中重叠社区的种子都是节点1与节点34，而(1)子图中的重叠节点是3，(2)子图中的重叠节点是9、3、14.该俱乐部实际也是以节点1与节点34为核心领导人物被划分成了两个团体，由此可知本文算法在karate club上划分的加权重叠社区结构具有较好的准确性.

图4 Karate club加权社交网络的重叠社区划分图Fig.4 The overlapping community structure of karate club weighted network

3.3.3算法在karate club、lesmis、netscience上的运行效率分析与对比

表1 EM-BOAD、LOC、UGDE的运行效率对比表

表1是算法的运行效率对比表，对其进行解析，将EM-BOAD算法、LOC算法、UGDE算法在加权网络karate、lesmis、netscience上测试时，所耗费的运行时间都与网络的规模成正比关系，即网络规模扩大，运行时间也加增.其中，EM-BOAD算法的时间花费代价最小，而本文提出的UGDE算法的运行时间相对最多，即该算法的运行效率是三者中最差的.

3.3.4算法在karate club、lesmis、netscience上的加权模块度对比

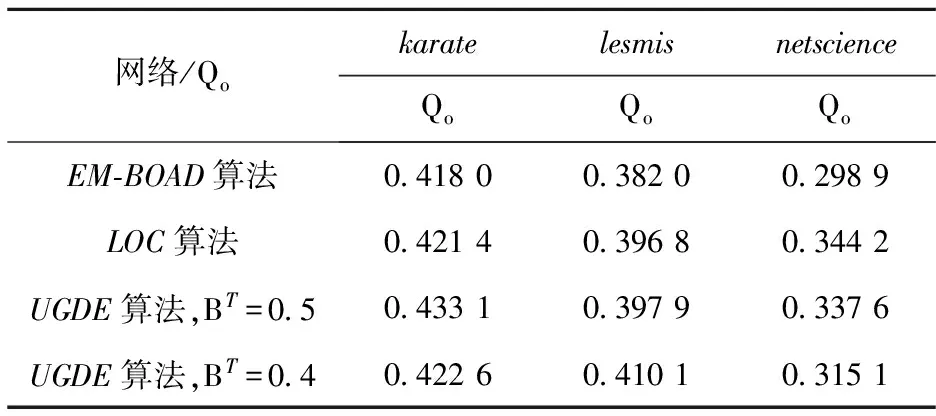
表2 EM-BOAD、LOC、UGDE的Qo对比表

表2是算法的Qo对比表，由对表2的剖析可得，在加权网络karate、lesmis、netscience上实验获取的加权模块度函数值中，EM-BOAD算法的Qo表现最差，即划分的重叠社区结构的结构化程度是三个算法中最低的；在karate、lesmis网络中，UGDE算法的Qo值都优于LOC算法的Qo值，此时UGDE发现的重叠社区结构的质量比LOC要好；而在netscience网络中，UGDE算法的加权模块度函数Qo值却微小于LOC算法的Qo值，即此时UGDE算法划分的重叠社区结构的模块化水平低于LOC.

3.3.5算法在astro-ph加权网络上的性能分析 本文在astro-ph这个大型的加权关系网络中获取不同规模的数据集进行测试，仍将UGDE算法与EM-BOAD算法、LOC算法的实验结果作比较，从而更加确切地解析本文算法的性能.图5是网络规模与算法运行时间的关系图；图6是网络规模与加权模块度的关系图，其中网络规模由横坐标表示，加权模块度由纵坐标表示.

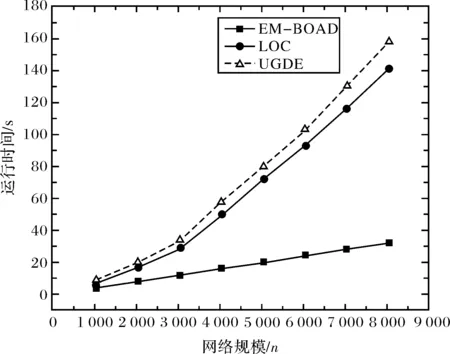
图5 网络规模与运行时间的关系图Fig.5 The relationship between network size and runtime

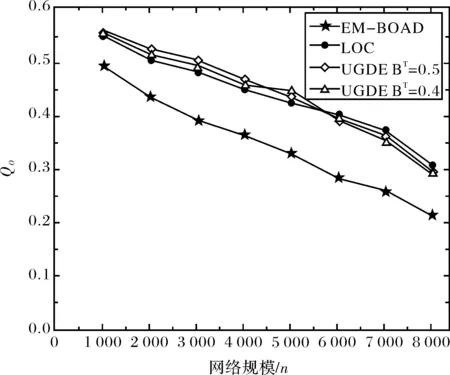
图6 网络规模与加权模块度Qo的关系图Fig.6 The relationship between network size and weighted modularity Qo

对图5进行解析，当astro-ph加权网络被用于实验测试的数据量按固定规模逐渐增加，EM-BOAD算法、LOC算法、UGDE算法的运行时间同时呈现出逐渐上升趋势，但本文的UGDE算法的时间递增相对速度最快，消耗的时间最多，执行效率相对较低.

对图6进行剖析可知， EM-BOAD算法、LOC算法、UGDE算法获得的加权模块度值与网络规模成反比关系，即随着astro-ph加权网络的节点个数递增，算法的Qo值却呈现出递减趋势.其中EM-BOAD的Qo值变小的速率最高，其划分效果最差，本文UGDE算法在节点数量从1 000按1 000节点的规模递增至5 000获得的Qo值都是三个算法中最良好的，但网络节点个数在5 000以上，UGDE算法的Qo值相对比LOC的Qo值略小.由此可知，UGDE算法划分的加权网络重叠社区结构具有较好的结构性与准确性，但在达到一定规模以上的大型网络中，其划分的重叠社区结构的结构性相对稍弱于LOC算法.

4总结

本文提出了基于联合引力度扩展的加权网络重叠社区划分算法，将带权节点的度与强度联合起来决定节点在加权网络中的影响力.在具体的加权网络上将算法做了运用测试，测试结果阐明UGDE算法花费的时间代价相对较高，该算法在实验的各个加权网络中获得的Qo值总体上大于EM-BOAD、LOC算法的Qo值，但仍有稍小于LOC算法的加权模块度值的情形，从而表明本文算法在划分加权网络的重叠社区结构上是有效可行的.我们后期研究工作将致力于进一步降低UGDE算法的运行时间，并改善本文算法在大型加权网络上发现的重叠社区结构的质量.

[1] JIERUI X， STEPHEN K， BOLESLAW K. Overlapping community detection in networks: the state-of-the-art and comparative study[J]. ACM Computing Surveys， 2013， 45(4): 1-43.

[2] BOSCHLOO L， SCHOEVER R， BORKULO C， et al. The network structure of psychopathology in a community sample of preadolescents[J]. Journal of Abnormal Psychology， 2016， 125(4): 599-606.

[3] PREM K， DAVID M. Efficient discovery of overlapping communities in massive network[J]. Proceeding of the National Academy of Sciences of the United States of America， 2013， 110(36): 4534-4539．

[4] CHUNYING L， YONGHANG H， ZHIKANG T， et al. Adaptive label propagation algorithm to detect overlapping community in complex networks[J]. International Journal of Future Generation Communication and Networking， 2016， 9(8): 317-326．

[5] SUNGSU L， SEUNGWOO R， SEJEONG K， et al. LinkSCAN: Overlapping community detection Using the link-space transformation[J]. ICDE， 2014， 30: 292-303．

[6] YU Z， DIY-YAN Y. Overlapping community detection via bounded nonnegative matrix tri-factorization[J]. ACM New York， 2012， 12(8): 606-614.

[7] HUANG L， GUISHEN W， WEI P， et al. A link density clustering algorithm based on automatically selecting density peaks for overlapping community detection[J]. International Journal of Modern Physics， 2016， 30(8): 1-15.

[8] DI J， BO Y， CARLOS B， et al. Markov random walk under constraint for discovering overlapping communities in complex networks[J]. Journal of Statistical Mechanics: Theory and Experiment， 2011， 31(5): 1-22．

[9] JING L， WEICAI Z， HUSSEIN A， et al. Separated and overlapping community detection in complex networks using multi-objective evolutionary algorithms[J]. IEEE Congress on Evolutionary Computation， 2010， 8: 1-7.

[10] 刘 倩， 刘 群. 基于引力度扩展的叠社区发现算法[J]. 计算机工程与设计， 2014， 35(3): 110-113．

[11] OPSAHL T， AGNEESSENS F， SKVORETZ J. Node centrality in weighted networks: generalizing degree and shortest paths[J]. Social Networks， 2010， 32(3): 245-251．

[12] JUNQIU L， XINGYUAN W， JUSTINE E. Detecting overlapping communities by seed community in weighted complex networks[J]. Physica A， 2013， 23(392): 6125-6134．

[13] CHEN D， SHANG M， LYU Z， et al. Detecting overlapping communities of weighted networks via a local algorithm[J]. Physica A: Statistical Mechanics and Its Applications， 2010， 389(19): 4177-4187．

[14] 乔秀全， 杨 春， 李晓峰， 等. 社交网络服务中一种基于用户上下文的信任度计算方法[J]. 计算机学报， 2011， 34(12): 2403-2413.

[15] 鹿 静， 徐 勇， 安丽平. 基于节点相似度的加权网络社团结构划分算法[J]. 信息与控制， 2012， 4(41): 504-508．

[16] 吕天阳， 谢文艳， 郑伟民， 等. 加权复杂网络社团结构的评价指标及其发现算法分析[J].物理学报， 2012， 21(61): 1-10．

[17] NEWMAN M E J. Finding community structure in networks using the eigenvectors of matrices[J]. Physical Review E， 2006， 74(3): 1-22．

Overlapping community detection algorithm based on expansion of union gravitational degree in weighted networks

SUN Yanwei1，2， LEI Jianjun2， YANG Jincai1

(1.School of Education Information Technology, Central China Normal University, Wuhan 430079; 2.School of Computer Science， Hubei University of Education， Wuhan 430205)

The overlapping community detection algorithm based on expansion of gravitational degree, which is mainly used to excavate overlapping community structure in social networks, is applied to un-weighted networks. Real community is more with weighted attributes, according to the seed strategy of GDE, and based on the characteristics of the weighted network, the core node of a community is able to be determined by its degree and strength. Here the over overlapping community detection algorithm based on expansion of union gravitational degree in weighted networks (UGDE) is proposed. According to experimental results, it demonstrates that the algorithm is efficient and feasible for detecting overlapping communities in weighted networks.

overlapping community; union degree; union gravitational degree; community detection; weighted network

2016-11-12.

国家社会科学基金项目(14BYY093).

10.19603/j.cnki.1000-1190.2017.04.004

1000-1190(2017)04-0435-06

TP393

A

*通讯联系人. E-mail: jcyang@mail.ccnu.edu.cn.