数列求和的基本方法和技巧

山东省滨州市博兴县博兴二中 李瑞芳

数列求和的基本方法和技巧

山东省滨州市博兴县博兴二中 李瑞芳

数列求和是数列的重要内容之一，也是高考中的必考内容。除了等差数列和等比数列有求和公式外，大部分数列的求和都需要一定的技巧。

等差数列；等比数列；求和；倒序相加；错位相减；分组；裂项

数列是高中代数的重要内容，又是学习高等数学的基础，在高考中也占有重要的地位。数列求和是数列的重要内容之一，除了等差数列和等比数列有求和公式外，大部分数列的求和都需要一定的技巧。下面，我对数列求和的基本方法和技巧进行总结。

一、利用等差、等比数列求和公式求和

利用等差、等比数列求和公式求和是数列求和的最基本最重要的方法。利用等差数列求和公式求数列的前n项和时，要注意对等差数列性质的灵活运用；在等比数列中，当公比是未知量时，求和时要注意对公比的范围进行讨论。

分析：先分析数列的形式，如果数列是等差数列，则利用等差数列的求和公式研究，如果数列是等比数列，则利用等比数列的求和公式进行研究，在利用等比数列求和公式时，要注意分公比q能否为1进行讨论。

二、倒序相加法求和

在推导等差数列的前n项和公式时所用的就是这种方法，该方法就是将一个数列倒过来排列，再把它与原数列相加，结合等差数列的性质，就可以得到从而求出数列的前n项和。

三、分组法求和

还有一类数列，既不是等差数列，也不是等比数列，但是若将这类数列中的每一项适当拆开，便可分为几个等差、等比数列的和或差，然后把它们分别求和，再将其合，并即可得到原数列的前n项和。

分析：从形式上看，该数列既不是等差数列，也不是等比数列，但是将此数列中的每一项都拆成两项以后，就分成了一个等差数列和一个等比数列的和，然后再根据等差数列和等比数列的求和公式分别求和就可以了。

四、裂项法求和

例4：（2014山东，19）已知等差数列{an}的公差为2，前n项和为Sn，且S1，S2，S4成等比数列，

（1）求数列{an}的通项公式；

分析：在求和的过程中，需要先将通项公式进行化简，能消去的消去，最后达到求和的目的。

解：（1）略。

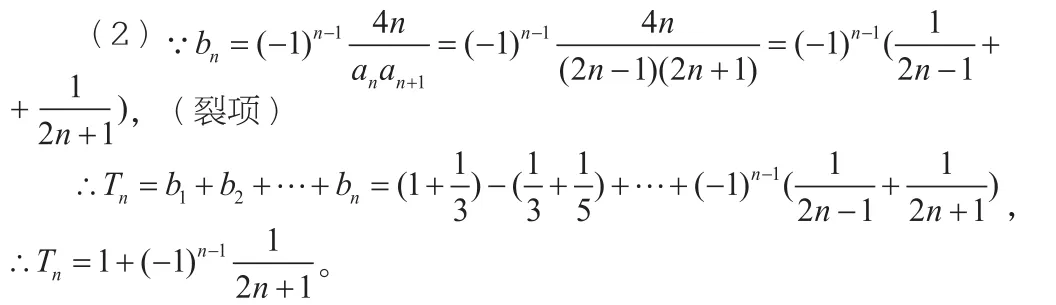
五、错位相减法求和

在推导等比数列的前n项和公式时，我们用的就是错位相减法求和，该方法主要用于求数列{an·bn}的前n项和，其中{ an}、{ bn}分别是等差数列和等比数列。2013年山东文理科高考题第20题，考查的就是错位相减法求和的知识。

例5：（2016山 东， 理18） 已 知 数 列{an}的 前n项 和是等差数列，且an=bn+bn+1。

（1）求数列{bn}的通项公式；

解：（1）略。

在求和的过程中，通常需要先求出其通项公式，再根据通项公式的形式进行适当的化简与求和，因此数列部分在求和过程中往往穿插着数列通项公式的求解，这也是数列部分的两大重点内容之一，后面我们继续研究。对于以上的各种方法，大家应注意体会其中所蕴含的分类讨论及化归的数学思想方法。当然，数列求和的方法还有很多，我们平时在教学中还应多注意总结。