基于分组和精英策略的遗传算法在机器人导航上的应用

谢忠红，王 培，顾宝兴，姬长英，田光兆

(1 南京农业大学 信息科学技术学院，江苏 南京 210095； 2 江苏省智能化农业装备重点实验室，江苏 南京 210031)

基于分组和精英策略的遗传算法在机器人导航上的应用

谢忠红1，王 培1，顾宝兴2，姬长英2，田光兆2

(1 南京农业大学 信息科学技术学院，江苏 南京 210095； 2 江苏省智能化农业装备重点实验室，江苏 南京 210031)

【目的】针对种植园复杂环境下采摘机器人进行路径规划时找出多路径效率低、速度慢等问题，提出一种基于分组和精英策略的遗传算法(GGABE)。【方法】首先生成1个初始群体，使用Sigmoid函数分组；然后在每组中分别进行选择、交叉、变异操作，进行n代迭代后，每组产生该组内的k条等长的最优路径；比较各组最优路径，选择最短的路径作为最优路径。在种群的各项参数均相同的情况下，简单遗传算法(SGA)、未分组的精英遗传算法(EGA)以及GGABE分别作用于15×15和25×25的地图，各进行 50 次试验。进行样机验证试验。【结果】第 1 幅地图，GGABE算法找到了 8 条最短路径，路径均值为 20.970 6，其他 2 种方法只能找出 1 条最短路径；第 2 幅地图，GGABE算法找到了 8 条最短路径，路径均值为 38.041 6。50次验证试验均找出 3 条最佳路径，平均路径规划时间为 15.543 319 s。【结论】本研究提出的基于分组和精英策略的遗传算法收敛速度快，可快速准确地在地图中搜索出所有能够遍历整个果园的最佳路径。

分组；精英策略；采摘机器人；遗传算法；优势个体；路径规划；导航

导航技术是采摘机器人研究领域中的关键技术，而路径规划则是导航研究课题中的重中之重，路径规划是指采摘机器人基于已给出的种植园地图，满足不碰撞障碍物的前提下，计算出一条从起点到终点的最短路径或耗时最少的路径[1-2]。张毅等[1]在遗传算法中新增了插入算子将间断路径转化为连续路径，删除算子用于删除路径中的冗余序号；卢月品等[2]使用Dijkstra算法找出1条可行、最短但不保证精度和安全性的路径，然后采用改进的遗传算法提高路径精度；张超等[3]结合混沌粒子群算法和遗传算法，提出了基于粒子群-遗传算法切换策略的路径规划方法；Kala[4]提出了在1张地图中使用多个机器人共同寻找最佳路径，由其中的某个主机器人协调它们之间的合作关系；Masoud等[5]提出了六边形环境建模法，可以在较短的时间内找出全局最佳路径；Yun等[6]为了提高搜索效率，在产生初始种群时，引入了障碍物避免算法(OAA)和区分算法(DA)；Mohanta等[7]在Petri网中引入了遗传算法，该算法基于一种迭代的、非线性搜索操作，能够充分利用环境的几何信息，产生适宜的航线角度。

已有的算法改进主要研究如何提高收敛速度，较少涉及从地图中获取多条最佳路径的问题；当搜索空间很大时，如何快速收敛到全局最优路径附近也是一个难题。针对这些问题，本文提出了一种基于分组和精英策略的遗传算法，以期快速、有效地获取地图中的所有最佳路径。

1 基于分组的改进遗传算法

基于Sigmoid函数对搜索空间分组后，在每组独立进行遗传操作，每一代适应度值最高的个体即为精英个体，将其完整保留到下一代中，并参与到每个个体的交叉和变异。

1.1 地图生成及编码

为了便于采摘机器人的移动，种植园中果树要求分布规则且间距较大(＞5 m)，而移动中的机器人机械手处于收拢状态，所占区域长宽在[1.0 m, 1.5 m]内，因此可将机器人视为质点。栅格法生成的种植园地图如图1所示，图1中的带箭头的线段表示1条路径。初始化群体可采用2种编码方式：坐标法和序号法。坐标法和序号法的转换关系分别如下，其中x为横坐标，y为纵坐标，z为序号。

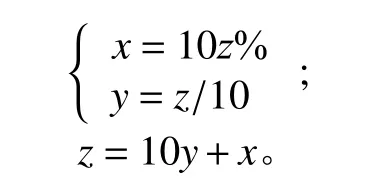
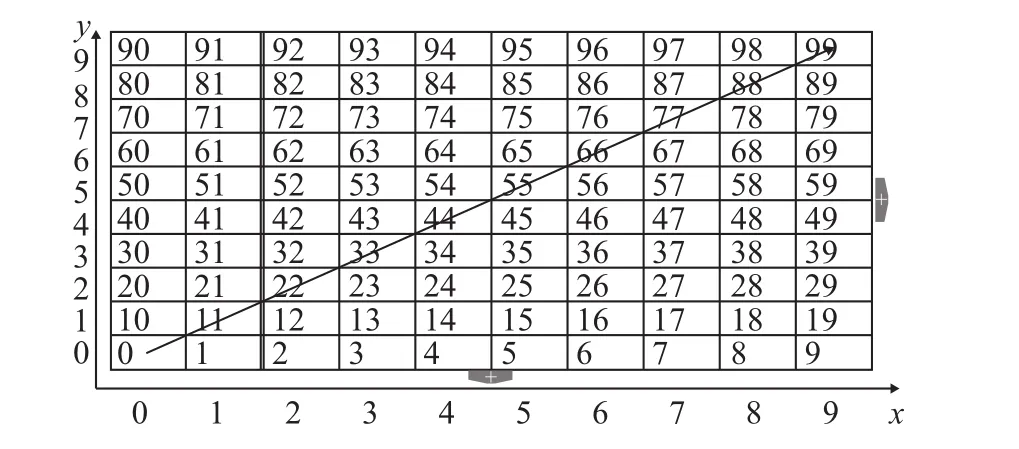
图1 坐标法和序号法表示的地图Fig. 1 Map indicated by coordinate and order

1.2 分组

对地图空间进行分组，使得种群在每组中分别进行遗传操作，其中分组数(k)是关键。k太大，适应度高的个体及其后代会很容易替代其他个体，导致陷入局部收敛；k太小，无法体现分组的优势[8-9]。

人为指定法分组：根据经验给出1个可行的分组数，缺点是主观差异大。动态分组法：分组数随着种群的进化不断动态变化。初始时种群中的个体呈随机分布，差异大，k取较大值；随着种群的进化，个体差异变小，逐渐收敛于n条最佳路径(n≥1)，此时k随之变小。研究中k遵循Sigmoid函数[10]，并结合了粗粒度并行遗传算法[11-12]。

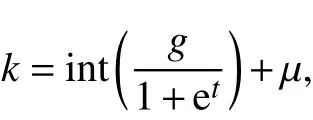
式中，g为初始分组数(5～8)，t为进化代数，μ是调整参数，一般取值为2。

首先初始化随机种群，设种群规模大小为n，即共有n条路径，po={pa1, pa2, …, pai…, pan}，po表示种群空间，pai表示第i个个体。初始设进化代数t=0，g=8，根据公式计算出分组数k=6。将种群空间po依次平均分为k组子种群，前k–1组子种群中，每个子种群有av=■n/k」个个体，最后1个子种群有[n−(k−1)av]个个体，分组后的种群空间po={{pa1,在每组中依次进行遗传操作，可以避免早熟收敛。

每进化1代执行遗传操作之前，在空间po中按■照一■定概率pswap，每2组之间随机交换个个体，即第1组和第2组，···，第k组随机交换个体，若k为奇数，则最后一组保持不变。通过引入新的个体，增加了每个子种群的多样性，避免了局部收敛；同时，每个子种群在搜索空间的不同部分分别进化，加强了全局搜索能力。

经过观察发现，当t∈[0, 5]时，分组数k均为6；当t∈[6, 10]时，k为5；当 t∈[11, 19]时，k为4；当t∈[20, 66]时，k为3；随着种群的进化，最后分组数k稳定为2。也就是说，种群在第6、11、20、67代时会按照上述方法重新进行分组，而在其他代数时，采用上一代的分组结果。

1.3 适应度函数

根据给定的目标函数，计算适应度值。最优路径满足以下准则：无碰撞；路径长度最短。碰撞函数f(ro)的公式为：

式中，ro指序号法表示的路径。

路径长度函数l(rc)的公式为：

式中，rc指坐标法表示的路径；为路径上相邻的方格；n为路径上的方格数。

移动路径的评价函数g(r)公式为：

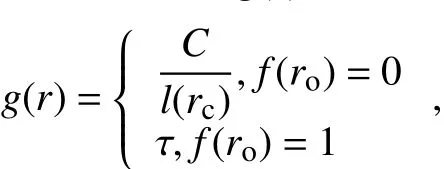
式中，C是放大系数；τ 是1个极小值。

显然当碰到障碍物时，适应度值低，繁殖后代的概率小。

1.4 遗传算子

精英个体指的是当前种群中适应度值最高的个体[13]，可能不止一个。种群中精英个体和全局最优解之间的“血缘关系”要大于其他个体和全局最优解的“血缘关系”，所以要充分利用精英个体中的遗传信息。本文结合精英保留策略和轮赌盘操作选择个体，将每组中的精英个体不加改变地保留到下一代，并参与每个交叉和变异操作。根据交叉概率Pc，在选择后的个体中进行交叉操作。采用单点交叉，在2个父本中相同点(起点和终点除外)前后交换。如2条路径分别为(0, 11, 12, 23, 34, 44)和(0, 10, 11, 22, 33, 44)，都经过方格11，在该点前后交叉，交叉后为(0, 10, 11, 12, 23, 34, 44)和(0, 11, 22, 33, 44)。若2条路径(除起点和终点外)没有相同点，则不交叉；有多个相同点，随机选取一个作为基准点，进行交叉。交叉的父本之一必须是上一代的最优值，这样能保护种群的精英个体，加快收敛速度。随机产生1个0～1之间的数w，若w小于变异概率pm，则进行变异操作，采用偏移节点方法[4]。首先，在待变异个体上任选一点(xi, yi)，其前驱节点和后继节点分别为(xi-1, yi-1)和(xi+1, yi+1)；然后，设置1个半径常数r，并在0～360之间取随机数θ，变异后的节点为(xi′, yi′)，公式为：

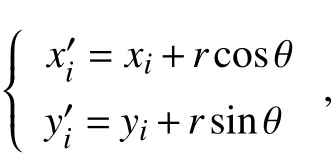
连接(xi-1, yi-1)和(xi′, yi′)、(xi′, yi′)和(xi+1, yi+1)，判断其是否经过障碍物，若经过，则舍弃该节点，重新生成一个节点并判断，直到满足条件为止；否则，用新节点替换旧节点。

2 算法收敛性分析

已知定理1：若随机过程或系统在t0时刻所处的状态已知，在t＞t0时刻所处的条件分布与t0之前所处的状态无关，则该过程或系统称为马尔科夫链[14]。

根据定理1得出结论 1：GGABE算法的种群序列{Xt,t≥0}是齐次马尔科夫链，其中t表示进化代数。证明如下：GGABE遗传算法中的选择、交叉、变异操作都是独立进行的，且每个子代都是由父代通过遗传操作得到的，与父代之前的个体无关。所以GGABE算法是齐次马尔科夫链。

结论 2：GGABE算法具有全局收敛性。证明如下：设S为种群状态空间，sk表示第k代最优解对应的适应度值，pk为得到最优值sk的概率，pk＞0，很显然，随着进

化过程的推进，第k+1代最优解的适应度值一定大于等于第k代最优解的适应度值，因此S空间是一个单调非递减的有序空间。pi,j表示由状态si迁移到状态sj的概率，由于GGABE遗传算法中每一代的最优个体都会复制到下一代中，除非下一代出现了适应度值更高的个体，否则这个最优个体会一直被保留，也就是说种群会一直向接近全局最优解的方向进化，而不会出现退化现象。因此，根据定理1，该算法的状态转移概率矩阵为：

(趋于无穷大)时，可以收敛到最优解，因而GGABE算法具有全局收敛性。

3 测试函数及结果

3.1 测试函数

选择了2个代表性的测试函数f1(x)和f2(x), 验证简单遗传算法(SGA)，未分组的精英遗传算法(EGA)和基于分组和精英策略的遗传算法(GGABE)的收敛率及收敛速度。f1(x)和f2(x)公式如下：

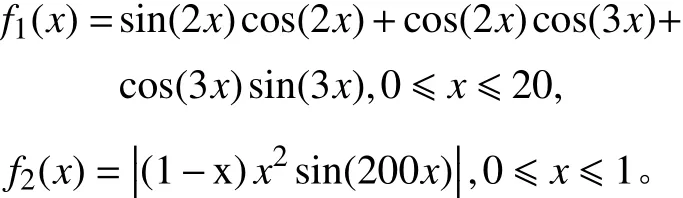
3.2 测试结果及分析

3种遗传算法分别执行200次，种群大小为20，最大遗传代数T为100，pc为0.99，pm为0.1，ηc和b均为2，pswap为0.6。根据函数图像中极值的分布对搜索空间进行人工分组，函数f1(x)分为4组；函数f2(x)不分组。以收敛率(sr)、平均收敛代数 (ast) 来评估算法性能[15]，结果如表1所示。

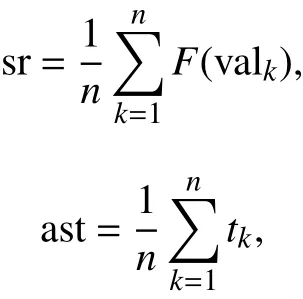
式中，n为执行次数，valk表示第k次试验计算的最优值，F(valk)表示valk是否收敛，收敛为1，否则为0，tk表示第k次试验结束时种群进化次数。

根据表1分析对于同一函数：SGA收敛率最低，收敛速度最慢，平均迭代数最大，计算出的最优值误差最大；GGABE收敛率最高，收敛速度最快，平均收敛代数最小，计算的最优值误差最小，f1(x)与实际最优值之差为 0.012，而f2(x)与实际最优值之差为0。GGABE能够找出多极值函数的所有最优解而SGA和EGA只能找出1个。函数f1(x)在[0, 20]内有4个最优解，200次试验中，GGABE算法有199次找出了4个最优值，而SGA和EGA算法每次均找出了1个最优值。

表1 3种遗传算法寻找函数f1(x)、f2(x)最优值的性能比较Tab. 1 Peformance comparision of three genetic algorithms searching optimal function f1(x) and f2(x)

4 寻找最优路径

4.1 试验设计

试验设备为一台华硕笔记本，基本配置: i7Intel处理器, 主频2.39 GHz，试验软件为Matlab2012A。设计了2幅不同规模的地图，第1幅为15×15(图2a、2b、2c)，第2幅为25×25(图2d、2e、2f), 地图中黑色区域为障碍物，左下角为起点，右上角为终点，实线为寻找到的最优路径(图2)。

图2 3种算法在不同规模地图上的搜索结果Fig. 2 Searching results of three algorithms on maps with different scales

4.2 结果分析

基于15×15和25×25的2幅地图进行路径搜索，3种算法的参数设置相同，种群规模30，循环100代，pm为0.10，pc为0.99，pswap为0.60，3种算法均执行50次。结果如表2所示。

由表2可知，在15×15规模的地图上进行路径搜索时，GGABE算法收敛代数最少，收敛率最高，达94%，在满足无碰撞条件下寻找到的最优路径长度最短，仅为20.970 6。由于试验中使用的地图中存在8条最优路径，GGABE算法正确地找出了8条路径，而其他2种算法只能找到1条路径，且不是最短路径，说明本研究算法性能卓越。

由表2可知，在25×25规模的地图上进行路径搜索时，SGA和EGA的收敛速度和收敛率大幅下降，SGA算法的收敛率降为0.14，EGA的收敛率也降为0.56，而GGABE的性能变化不大，收敛率仅下降了0.04，最大收敛代数仅增加了4代，找到的最佳路径数是全部的8条。由此可见，即使在搜索空间增大的情况下，GGABE依然能够正确地找出所有的最佳路径，且有良好的收敛率和收敛速度。

表2 3种遗传算法在不同大小规模的地图中搜索路径时性能比较Tab. 2 Performance comparision of three genetic algorithms searching paths on maps with different scales

4.3 验证试验

为了测试GGABE的性能，2017年在江苏省徐州市丰县宋镇楼的苹果园进行了样机测试。果树行距为4.0 m，株距为3.7 m，以安装了机械臂和扫描仪的履带驱动农业机器人为研究平台，在苹果园中规划路径。机器人的移动速度为0.68 m·s–1，行走路径为果树行中心线。为防止破坏果树，机器人移动过程中收起机械臂，可看成一个质点。果园最佳路径必须满足2个条件：无碰撞(即不经过障碍物)；满足前面条件的前提下，保证路径长度最短。

为实现自动导航，需要确定果树位置信息。以扫描仪中心为坐标原点，机器人前进方向为x轴，建立直角坐标系。扫描仪射出的激光会在树干上形成1个交点，作为此树的标识，提取该点在坐标系中的坐标，就获得了果树位置。获得的位置坐标信息传入后台计算机，机器人可在GPS的帮助下移动。将果园栅格化为30×30地图(图3a)，黑色区域为果树，浅色网格为人为添加的障碍物，由起点至终点，由控制计算机基于GGABE算法找出1条或若干条遍历果园内所有果树的最佳路径，并发送控制指令驱动机器人前进。进行50次试验，计算机每次均找出3条最佳路径(图3b、3c、3d)，人为选中1条路径供机器人行走，前10次和后10次试验路径规划花费的平均时间分别为15.700 817 s和15.608 967 s；50次试验中最长规划时间为15.724 909 s，最短规划时间为15.184 906 s，平均时间为15.543 319 s。

图3 验证试验Fig. 3 Verification experiment

5 结论

本文针对传统遗传算法效率低、收敛速度慢且无法处理多极值的问题，提出了一种基于分组和精英策略的遗传算法，并将其应用在采摘机器人路径规划研究中。研究中设计了15×15和25×25的2幅仿真地图，GGABE算法能以最快的速度，最高的收敛率找出所有正确的最短路径，而另外2种算法只能各找出1条路径，且不是最优。当搜索空间规模增大时，本文提出的算法依然能够快速收敛，找到多条最优路径。可见GGABE算法具有良好的鲁棒性和收敛速度。实地试验表明在庞大而复杂的果园中，GGABE算法依然能躲避障碍物，快速准确地找出所有遍历整个果园的最佳路径，本研究为后期机器人实现采摘任务提供了基础。

由于初始种群的优劣对路径规划有一定的影响，本文中初始种群为随机产生，今后将重点研究如何获得优质的初始种群，从而进一步提高算法的收敛率和收敛速度。

[1]张毅, 代恩灿, 罗元. 基于改进遗传算法的移动机器人路径规划[J]. 计算机测量与控制, 2016, 24(1): 313-316.

[2]卢月品, 赵阳, 孟跃强, 等. 基于改进遗传算法的狭窄空间路径规划[J]. 计算机应用研究, 2015, 32(2): 413-418.

[3]张超, 李擎, 董冀媛, 等. 基于混沌粒子群—专用遗传算法切换策略的移动机器人路径规划[J]. 北京科技大学学报, 2013, 35(6): 826-830.

[4]KALA R. Multi-robot path planning using co-evolutionary genetic programming[J]. Expert Syst Appl, 2012, 39(3): 3817-3831.

[5]MASOUD S, MOHD F O. Global path planning for autonomous mobile robot using genetic algorithm[C]//Signal-Image Technology and Internet-Based Systems, 2013 International Conference. USA: IEEE, 2013: 726-730.

[6]YUN S C, GANAPATHY V, CHONG L O. Improved genetic algorithms based optimum path planning for mobile robot[C]//Control Automation Robotics and Vision, 2010 11th International Conference. USA: IEEE, 2010: 1565-1570.

[7]MOHANTA J C, PARHI D R, PATEL S K. Path planning strategy for autonomous mobile robot navigation using petri-GA optimisation[J]. Comput Electr Eng, 2011, 37(6): 1058-1070.

[8]童俊华, 蒋焕煜, 周鸣川. 基于遗传算法的穴盘苗自动移钵路径优化[J]. 农业机械学报, 2013, 44(4): 45-49.

[9]BERCLAZ J, FLEURET F, TURETKEN E, et al. Multiple object tracking using k-shortest paths optimization[J]. IEEE T Pattern, 2011, 33(9): 1806-1819.

[10]CHEN D Z, HERSHBERGER J, WANG H. Computing shortest paths amid convex pseudodisks[J]. SIAM J Comput, 2013, 42(3): 1158-1184.

[11]王峰, 曼媛, 段俊洁. 一种改进的求解前N条最短路径问题的多种标号算法[J]. 小型微型计算机系统, 2016, 37(7): 1482-1487.

[12]岳钦, 冯珊. 粗粒度并行遗传算法的计算性能分析[J].武汉理工大学学报, 2008, 30(7): 107-110.

[13]TSAI C C, HUANG H C, CHAN C K. Parallel elite genetic algorithm and its application to global path planning for autonomous robot navigation[J]. IEEE Trans Ind Electron, 2011, 58(10): 4813-4821.

[14]庄嘉祥. 精英策略遗传算法改进及在作物模型参数优化的应用[D]. 南京: 南京农业大学, 2013.

[15]罗熊, 樊晓平, 易晟, 等. 具有大量不规则障碍物的环境下机器人路径规划的一种新型遗传算法[J]. 机器人, 2004, 26(1): 11-16.

【责任编辑 霍 欢】

Application of genetic algorithm based on group and elite strategy for robot navigation

XIE Zhonghong1, WANG Pei1, GU Baoxing2, JI Changying2, TIAN Guangzhao2
(1 College of Information Technology, Nanjing Agricultural University, Nanjing 210095, China; 2 Intelligent Agriculture Equipment Key Laboratory in Jiangsu Province, Nanjing 210031, China)

【Objective】To solve the problems that picking robot could not find the multipath quickly and accurately in planning route in complex plantation environment, a genetic algorithm based on group and elite strategy (GGABE) was proposed.【Method】Firstly, an initial population was generated and was divided into several groups using the Sigmoid function. After n times of operations of selections, crossovers and mutations in each group separately, k optimal paths with equal length were then acquired in each group. Comparing the optimal paths among different groups, the shortest paths were chosen as the final optimal paths. With all population parameters being the same, three types of algorithms, including simple genetic algorithm(SGA), ungrouped elite genetic algorithm (EGA) and GGABE, were tested 50 times respectively on 15×15 and 25×25 maps. The prototype verification experiments were carried out in the plantation.【Result】Eight shortest paths with the average length of 20.970 6 were found in map 1 by GGABE. Only one shortest path was found in map 1 with the other two algorithms. Eight shortest paths with the average length of 38.041 6 were found in map 2 by GGABE. Three optimal paths were found in each of the 50 verificationexperiments, and the average consumption time for route planning was 15.543 319 s.【Conclusion】GGABE has fast convergence speed and can quickly and accurately find out all optimal paths, which are able to traverse the entire plantation, from the map.

group; elite strategy; picking robot; genetic algorithm; advantageous individual; route planning; navigation

TP242; S233

A

1001-411X(2017)05-0110-07

谢忠红, 王培, 顾宝兴, 等. 基于分组和精英策略的遗传算法在机器人导航上的应用[J]. 华南农业大学学报, 2017, 38(5): 110-116.

2016-12-30 优先出版时间：2017-07-14

优先出版网址：http://kns.cnki.net/kcms/detail/44.1110.s.20170714.0859.038.html

谢忠红(1977—)，女，副教授，博士，E-mail: xiezh@njau.edu.cn

国家自然科学基金(31401291)；江苏省自然科学基金(BK20140720)；中央高校基本业务费(KYZ201670)