高维非线性随机微分方程组的指数稳定性
2017-08-07王小芹常萌萌秦志芳
王小芹,常萌萌,秦志芳
(安阳学院数学教研室,河南安阳455000)
高维非线性随机微分方程组的指数稳定性
王小芹,常萌萌,秦志芳
(安阳学院数学教研室,河南安阳455000)
随机系统的稳定分析,近年来逐渐受到很多概率论学者与工程技术人员的研究,并取得了重要的研究成果,而前人研究往往以Lyapunov方法为工具,从系统的生成元入手,得到系统稳定性的依据.文章从随机微分方程组的变换入手,将随机微分方程组局部的变换为带随机项的常微分方程组,然后通过类似于Hurwitz的分析技巧,从而得到系统的指数稳定性判据.
Lyapunov稳定;随机微分方程组;连续半鞅;It^o公式;指数稳定性
随机微分方程是建立在概率论与常微分方程稳定性理论的边缘上发展起来的,其研究领域是非常广泛的,其中随机微分方程的稳定性研究是最为重要的一面[1-2],无论是对学术理论,还是实际应用方面都非常有意义.
随机微分方程稳定性的发展,是从1908年,Langevin在研究Brown运动时首次得到一随机微分方程开始的,到1951年,It^o建立It^o型随机微分方程的理论,为后来学者给出随机微分方程稳定性的几种释义奠定了基础.直至1994年,毛雪荣全面讨论了随机微分方程和随机泛函微分方程的指数稳定性,该研究是从系统的生成元入手,以Lyapunov方法为工具,对随机系统进行研究.
1 预备知识
1.1 微分动力系统
定理1[1]考虑该随机微分方程

其中的b(x),σ(x)是Rm上的两个连续函数,如果存在两个正整数K和K-,满足
(1)(Lipschitz)对任意的x,y∈Rd,t∈[0,T],有:

(2)(线性增长条件)对任意的(x,t)∈Rd×[0,T],有:

则方程dX(t)=b(X(t),t)dt+σ(X(t),t)dW(t)存在唯一的一个解X(t),并且X(t)∈M2([t0,T],R).
定理2[3]当且仅当对于任意给定的正定对称矩阵Q,存在一个正定对称矩阵P满足Lyapunov方程,即

那么A就是Hurwitz矩阵,即A的所有特征值都满足Reλi<0.此外,如果A是Hurwitz矩阵,那么P就是Lyapunov方程的唯一解.
定理3[3]设x=0是非线性系统的一个平衡点,其中有连续可微函数f:D→Rn,且D为原点的一个邻域.设

(1)原点是渐近稳定的,若A的所有特征值都满足Reλi<0.
(2)原点是不稳定的,若A至少有一个特征值满足Reλi>0.
1.2 鞅、布朗运动和It^o公式
定义1[2]Ft适应过程X=Xt,t∈Rt为一维连续半鞅,它具有下面唯一的分解式:

其中X0为F0可测随机变量,Mt为连续局部鞅,Vt为连续有界变差过程,M0=V0=0.定义2[2]连续随机过程Bt:0#t<T{
}称为标准布朗运动,如果满足以下条件:
(1)B0=0,
(2)Bt是独立增量,即
0#t1<t2<...<tn<T,Bt2-Bt1,Bt3-Bt2,...,Btn-Btn-1是相互独立的,
(3)对任意0#s#t<T,Bt-Bs服从期望为0,方差为c2t的正态分布,
(4)t0,Bt(ω)是关于t的连续函数.
则It^o公式又可写为

1.3 稳定性定义
定义3[3](指数稳定)如果
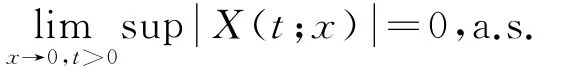
那么称(1)的平凡解是稳定的,否则称为是不稳定的.
如果存在γ>0使得
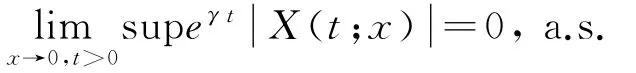
则称(1)的平凡解是指数稳定的.
2 主要结果及证明
考虑方程(1),其中b(x),σ(x)是Rm上的两个连续函数,满足以下条件:
1)b(x),σ(x)是连续可微的;
2)存在常数M>0,使得b(x)+σ(x)<M(1+x);
由随机微分方程的知识可知方程(1)存在唯一解,记方程的解为X(t;x0).假设
3)0是b(x)和σ(x)的唯一的0点,并且σ(0)不为0.
条件(3)说明x(t)≡0是方程(1)的一个解,称为平凡解或者平衡点.
首先假设m>1,d=1.设A=(aij)i#n,j#r是一个n×r矩阵,n维向量视为n×1矩阵.对于实数x,约定:
x*A=A*x=(xaij)i#n,j#r
设A(s)=(aij(s))i#n,j#r和B(s)=(bij(s))i#n,j#r分别是n×r和n×l矩阵函数,如果每个aij(s)和bij(s)都是连续半鞅,矩阵

记作〈dA(s),dB(s)〉.不难验证以下等式成立:
dA(s)B(s)=[dA(s)]B(s)+A(s)[dB(s)]+〈dA(s),dB(s)〉.设A是一个n×n矩阵,W(t)是一个一维布朗运动,令
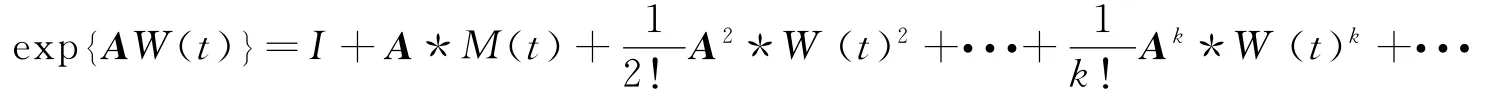
不难验证

当A和B可交换时
exp{(A+B)W(t)}=exp{BW(t)}exp{AW(t)}.
令A=σ(0),σ(x)和Ax是光滑C2-等价的,H是σ(x)和A(x)之间的C2-共轭映射.
由C2-共轭的定义,可知
H(x)σ(x)=AH(x),x∈Oρ(0)
上式两端求导后可得H(0)A=AH(0),即矩阵H(0)和A之间是可交换的.
设x0∈Oρ(0),X(t;x0)是方程(1)的解,简记作X(t).令

由It^o公式,知
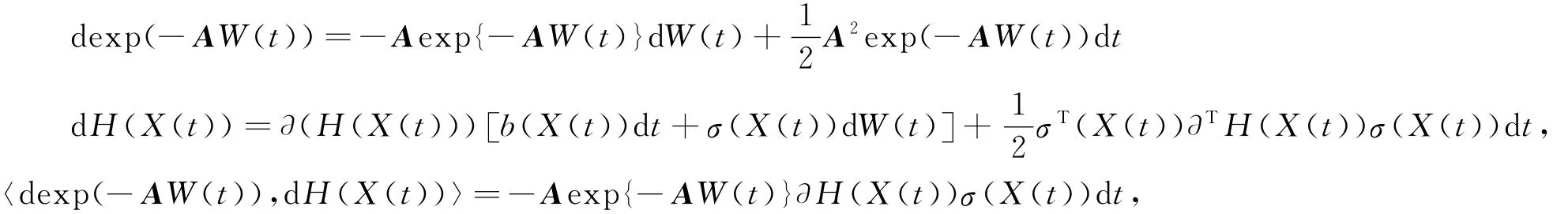
则
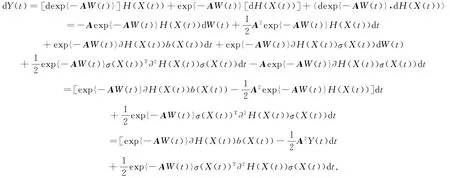
H(x)的逆映射记作G(y),则G(0)=H-1
令
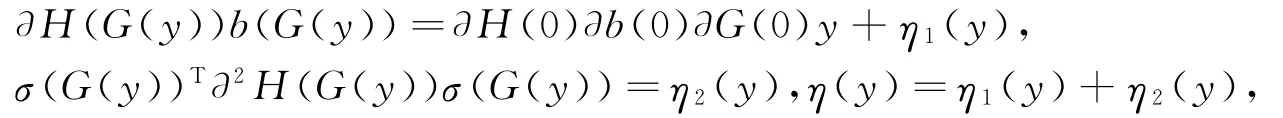
这样得到在(0,S)上

由于A与G(0),exp{-AW(t)},H(0)以及exp{AW(t)}是可换的,所以(1)可转化为
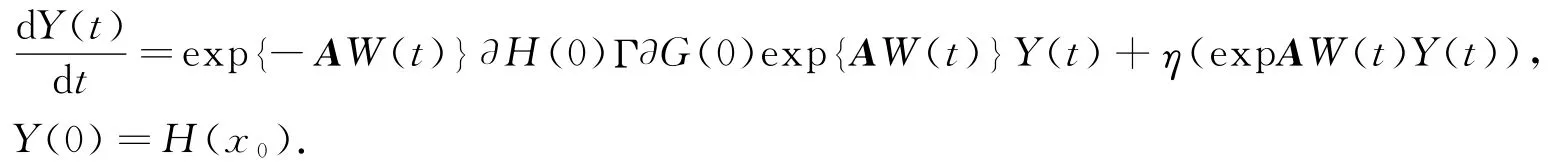
令E=H(0)ΓG(0),那么
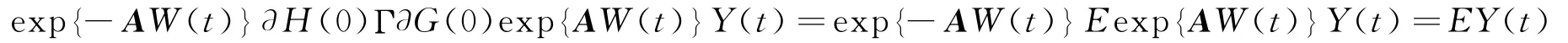

这时方程组转化为它是一个含随机项的常微分方程组.
定理4 假设b(0)与A是可交换的,如果Γ的所有特征值的实部都是负数,则方程组(1)的平凡解是指数稳定的.
证 令E=H(0)ΓG(0),那么由于E的特征值的实部全是负的,由定理3,可取m×m正定矩阵P使得
PE+ETP=-I.
令V(x)=xTPx,则由于P为正定矩阵,故有λmin‖Y(t)‖2#V(Y(t))#λmax‖Y(t)‖2,
其中λmin为V(Y(t))特征值的最小值,λmax为V(Y(t))特征值的最大值.
那么有
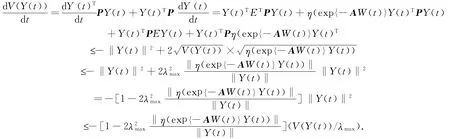
取ε>0,使得1-2λ2maxε>0.
令
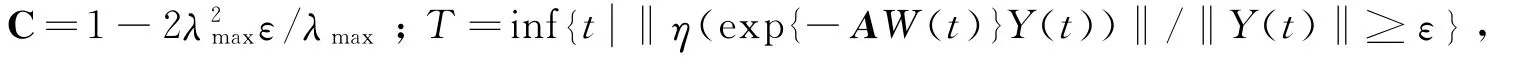
则在[0,T]上,有V(Y(t))#e-ctV(Y(0))#λmaxect‖Y(0)‖2.
由于exp{-AW(t)}是每个元素都含有-eαiW(t),W(t),cosβiW(t),sinβiW(t)的多项式,故由Brown运动的重对数律知,e-ctexp{-AW(t)}是一个有界函数,其界为N.
令τ=inf {t‖Y(t)‖γ},取Y(0)=H(x0),使得‖Y(0)‖<γ,则‖Y(τ)‖=γ.从而在[0,τ)上,V(Y(t))#e-ctV(Y(0)).
如果{t‖Y(t)‖γ}不空,则λmin‖Y(τ)‖2#V(Y(τ))#e-ctV(Y(0))#e-ctλmax‖Y(0)‖2.从而有γ
3 小结
文中方程组的指数稳定性的判据,仅需要随机系统系数在平衡点的导数,因此判据更具实用性.还可以进一步讨论,什么条件下,方程组(1)的平凡解是不稳定的.
[1]胡进.一类随机微分方程的稳定性分析[D].成都:电子科技大学,2006.
[2]谢晶晶.一维随机微分方程的稳定性[D].湖北:华中科技大学,2011.
[3]吴小太.几类随机微分方程解的存在与稳定性的研究与应用[D].东华大学,2012.
[4]胡宣达.关于随机微分方程的不稳定性定理[J],南京大学学报,1986,22(1):9-16.
[5]Khalil.非线性系统[M].北京:电子工业出版社,2005:60-73.
O211.62
A
1671-9476(2017)02-0032-04
10.13450/j.cnkij.zknu.2017.02.008
2016-08-15;
2016-11-23
王小芹(1990-),女,河南新乡人,硕士研究生,主要从事马氏过程分析研究.
