基于FNN解耦纸张定量水分控制策略的研究与应用

胡亚南 马文明,* 王孟效

(1.西京学院，陕西西安，710021；2.陕西西微测控工程有限公司，陕西咸阳，712000)



·定量水分控制策略·

基于FNN解耦纸张定量水分控制策略的研究与应用

胡亚南1马文明1,*王孟效2

(1.西京学院，陕西西安，710021；2.陕西西微测控工程有限公司，陕西咸阳，712000)

针对纸张抄造过程中纸张定量与水分之间存在强耦合的问题，提出一种模糊神经网络(Fuzzy Neural Network，FNN)的解耦控制器，首先利用模糊控制对控制系统进行耦合补偿，然后利用神经网络的自学习、自调整能力不断在控制过程中优化模糊控制规则及解耦补偿参数，成功地将纸张抄造过程的多变量系统转变为单变量系统，实现纸张定量、水分之间的解耦。仿真结果表明，采用FNN解耦控制器具有较好的动态响应和较强的鲁棒性。将该策略应用于国内某造纸厂的纸板机控制系统，纸张定量控制精度为±3.9 g/m2左右，水分控制精度为±1.0%左右，满足该纸机定量水分高精度控制要求。

定量；水分；模糊控制；神经网络；FNN

纸张的主要质量指标有定量、水分、厚度、松厚度、紧度、平滑度、白度、匀度、强度等20余项，其中纸张的定量和水分指标不仅是需要严格控制的质量指标，同时也影响厂家经济效益。图1所示为纸张抄造过程工艺流程图。纸张定量的控制是通过改变定量阀门开度以调节流浆箱的布浆浓度进行的，纸张水分的控制是通过改变主蒸汽阀门开度调节进入烘缸热蒸汽量进行的。当主蒸汽阀门开度变大引起纸张水分含量降低的同时纸张定量也减少，同样，当定量阀门开度变大引起纸张定量增加的同时纸张水分也提高。可见，定量阀门或主蒸汽阀门开度变化时，都会同时引起纸张定量、水分进行相应的改变。因此，纸张定量和水分控制系统是多变量耦合系统[1]。解耦的本质是通过对具有耦合的多输入多输出(MIMO)控制系统添加适当的补偿器，把控制系统解耦成多个独立的单输入单输出(SISO)系统或使控制系统耦合作用限制在一定程度内[2]。然而，纸张抄造过程受到纸浆的浓度和流量、热蒸汽的过热度和压力、纸机车速、铜网与毛毯的磨损老化等30多个因素影响，难以建立系统精确的数学模型，所以基于精确数学模型的解耦控制和最优控制在定量水分控制系统中难以取得良好的控制效果。

图1 纸张抄造过程工艺流程图

模糊控制算法和神经网络算法均具有不依赖于被控对象的精确数学模型即可适用于滞后、时变、非线性控制系统的特点[3-5]。由于两种智能控制算法各自具有局限性，所以本课题结合两种控制算法的优点，取长补短，集模糊逻辑推理的强大结构性知识表达能力与神经网络的强大自学习能力为一体，设计一种FNN(Fuzzy Neural Network)解耦控制器。依据模糊算法确定神经网络层数、层节点数及网络初值，利用神经网络自学习、自修正能力训练模糊规则，获得适合于系统实时控制的模糊规则。运用Matlab软件对FNN解耦控制器进行仿真，以验证该控制系统的解耦效果和鲁棒性。

1 纸张定量水分数学模型

纸张抄造过程的定量水分控制系统是一个存在严重的耦合和时变的两输入两输出的系统。从定量阀门和主蒸汽阀门开度变化，反映到卷取部纸张定量水分含量的变化过程均可以用式(1)表示。

(1)

式中，Gij(s)为第i个输出量对第j个输入量之间的传递函数(i，j=1，2)， Kij为静态增益，Tij为时间常数，τij为滞后时间。

用简单的飞升曲线法对纸机进行降阶处理，最后得到简化的定量水分控制系统模型如式(2)所示[6-7]。

(2)

式中，r1、r2分别代表定量阀门和主蒸汽阀门开度；y1、y2纸张定量和水分。

2 FNN解耦算法

神经网络拥有自学习、自适应能力，可以逼近任意非线性函数，具有容错能力强和鲁棒性好的优点，其局限性是网络层数、层节点数、网络初值的选取没有较好的实用方法，限制其泛化能力[8]；模糊控制依据控制规则输出控制信息，具有处理复杂、非线性系统的优越性，而其控制规则易受人为主观因素影响，稳定性较差，且没有自学习能力，时变跟踪能力差。将模糊控制与神经网络结合起来，以模糊集 、模糊逻辑为主，结合神经网络的方法，利用其自组织性，达到柔性处理信息的目的，使其具备学习和修正控制规则的能力，具有较好的适应能力和鲁棒性。

2.1FNN纸张定量水分解耦控制系统

FNN纸张定量水分控制系统的方框图如图2所示，其中sp1、sp2表示定量设定值、水分设定值；Y1(s)、Y2(s)表示被控量的定量、水分；Gc1(s)、Gc2(s)表示定量控制器传递函数、水分控制器传递函数；FNN1、FFN2表示定量解耦控制器、水分解耦控制器；Gw1(s)、Gw2(s) 表示定量阀门传递函数、主蒸汽阀门传递函数；G11(s)、G21(s)、G12(s)、G22(s)表示控制量与被控量之间的传递函数；Gk1(s)、Gk2(s)表示定量检测传感器、水分检测传感器。由图2可知，纸张定量、水分是相互影响的，在改变定量阀门开度调节进浆量时定量和水分都会产生变化。同样，调节主蒸汽阀门开度时定量和水分都会发生变化。这样的耦合关系相互影响，本课题的纸张定量水分解耦控制器由2个FNN构成，每个FNN解耦控制器都是单输出，每个FNN只负责单通道的解耦任务，所以不需要考虑解耦控制器之间的耦合作用。在解耦控制器的作用下，总的目标函数被解耦成单一的目标函数，所以使用传统的控制器就可以实现被控系统的闭环特性，获得较好的控制效果。

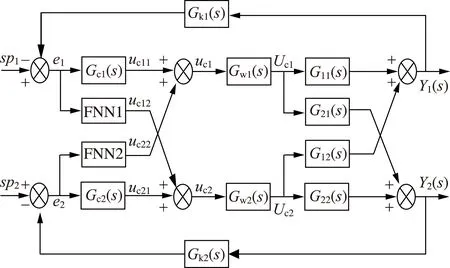
图2 纸张定量水分控制系统的方框图

2.2FNN解耦控制算法设计

图3是图2纸张定量水分控制系统中FNN解耦控制器的结构图，其中，k1、k2、k3分别是FNN解耦控制器输入量的量化因子和输入量变化率的量化因子及比例因子。FNN解耦控制器是以模糊控制为主体，应用神经元网络，实现模糊控制的决策过程，以模糊算法的结构选择神经网络的层数及各层节点数，以模糊控制方法为“样本”，以定量水分的误差值及误差变化率为解耦器输入值对神经络进行离线训练学习，学习后的神经元是一个聪明、灵活的模糊规则表，适合于系统实时控制的模糊规则，所以FNN具有自学习能力从而提高控制器的精确度和鲁棒性[9]。

图3 FNN解耦控制器结构图

从图3可见，根据模糊算法结构将神经网络划为5层，分别为输入层、模糊层、规则层、归一化层、输出层。

输入层的节点数为2，其作用是将输入值x=(x1，x2)(此处x1表示误差，x2表示误差变化率)传送到模糊层[10]。

(3)

式中，i=1，2是输入量个数，j=1，2…，7是模糊集合划分子集数。

本课题采用高斯函数为隶属度函数，即式(4)。

(4)

归一化层的作用是进行归一化计算，其节点数与规则层的节点数同为49个，见式(5)。

(5)

神经网络最后一层为输出层，其作用是把模糊推理的规则转化为对执行机构控制输出的精确量，即式(6)。

(6)

式中，vi，j表示第j个语言值隶属度函数的中心值。

2.3 FNN解耦控制系统的训练

FNN的权值矩阵R和补偿矩阵V利用Mamdani的模糊控制表进行离线状态下粗略模型修正，不停地变化纸张定量、水分的设定值(sp1、sp2)，经FNN进行正向计算出控制增量(Δuc1、Δuc2)作用于定量阀门和主蒸汽阀门，由纸张定量、水分模型计算出下一采样周期结束时定量、水分的采样值与其设定值进行比较，获得新的变量误差及误差变化量对误差不断修正权值矩阵R和补偿矩阵V。 为避免每次修正过多的参数而造成计算机大量计算而影响反应速度，所以FNN中各参数修正采用最大隶属度法。由于纸张定量水分调节的执行器是定量阀门和主蒸汽阀门，所以FNN控制器的输出为阀门开度[11-12]。假设调节阀门开度与流量成正比关系，且中浓浆浓度及蒸汽压力变化很小时，可以认为有式(7)。

(7)

式(7)用于估算定量阀门、主蒸汽阀门开度的误差，由于误差对FNN是反向传递进行网络训练学习，所以误差的精度并不影响最终控制精度，则有公式：

(8)

vij=vij+φijEjxi

(9)

(10)

式中，φij、φij是神经网络的学习系数，其值的大小决定系统的稳定时间和振荡时间长度。

图4 纸张定量水分控制系统方框图

3 纸张定量水分FNN解耦控制系统仿真

以浙江某纸厂(生产定量250g/m2的纸板)纸板机为例，建立控制对象模型，以传统PID为控制器，以FNN为解耦控制器；设计纸张的定量水分(主蒸汽流量-纸张水分、中浓浆流量-纸张定量)两输入两输出解耦控制方案，如图4所示。

利用MATLAB/Simulink进行仿真研究，输入信号选取方波信号代替传统的阶跃输入，来模拟工业现场中某一操作量发生突变或出现扰动的情况，在FNN控制器中输入层的误差及误差变化率的量化因子和输出层的控制输出的比例因子根据当前控制通道的传递函数进行调节，仿真结果如图5所示。

图5 纸张定量、水分Simulink仿真图

从图5可以看出，不同时刻的方波响应曲线之间存在的耦合现象在经过短暂时间的震荡后可被迅速消除，整体曲线震荡不大，输出曲线变化不明显，基本达到要求。其中，仿真曲线有跳变，是因为控制器未对系统完全实现动态解耦，等这一动态变化的过渡过程结束后，系统输出恢复为设定值，系统的静态解耦得以实现。观察仿真结果，控制器解耦控制效果良好，基本实现了耦合变量间的独立控制，并且具有响应曲线超调量小，响应速度快的特点。

图6 时间常数增加20%后的响应曲线

考虑到现场各种干扰因素和数学模型不精确的问题，以纸张定量控制为例验证解耦控制器的适应能力，将传递函数G11(s)，G12(s)的时间常数T1、T2增大20%进行仿真实验，结果见图6。由图6可知，定量控制主通道传递函数G11(s)参数改变后系统的响应速度虽然变慢，但仍无超调；耦合通道的传递函数G12(s)参数改变后，响应曲线也无较大变化，证明模糊解耦控制器的控制效果良好，对被控对象有较强的适应性。

以水分控制系统为例验证解耦控制的鲁棒性，在时间为50s时添加30%的阶跃干扰信号后纸张水分响应曲线见图7，由图7可以看出，水分响应曲线受到干扰影响迅速上升，超调量为16%，响应曲线约震荡10s后干扰被消除纸张水分曲线回归设定值，由此可见控制系统具有较好的适应能力和鲁棒性。

图7 添加30%干扰量后的纸张水分响应曲线

4 成果测试与应用

本课题提出的纸张定量水分解耦控制策略已经成功应用到国内某纸厂的纸板机控制系统上。该纸厂的FNN纸张定量水分控制系统投入运行之前，纸板定量、水分偏离设定值较大(定量偏离设定值±10g/m2左右，水分偏离设定值±4%左右)且定量、水分历史曲线变化频繁，系统鲁棒性较差。

图8 纸张定量、水分现场监控趋势曲线

图9 FNN纸张定量、水分正常运行显示界面图

在FNN纸张定量、水分控制系统正常运行后，由FNN纸张定量、水分现场监控趋势曲线(见图8)可知，纸张定量的设定值为310.0g/m2、最大值为313.9g/m2、最小值为306.2g/m2，纸张定量误差范围±3.9g/m2。纸张水分设定值8.2%、最大值为8.7%、最小值8.0%，则纸张水分误差范围±0.5%。由FNN纸张定量、水分正常运行显示(见图9)可知，纸张定量设定值为247.7g/m2、最大值为251.6g/m2、最小值为244.8g/m2，纸张定量误差范围±3.9g/m2。综合图8和图9，FNN纸张定量、水分控制系统(定量偏离设定值±3.9g/m2，水分偏离设定值±0.5%)，满足纸张定量水分控制精度(该纸板生产合格精度指标：定量为±5.0g/m2，水分为±2.5%)。

5 结 论

经模糊神经网络(FNN)纸张定量、解耦控制系统在实际运行中成功应用表明，无需建立纸板机纸张定量、水分的精确模型，即可利用神经网络的自学习、自调整能力，不断优化模糊控制的控制规则和调整解耦补偿参数，成功地将纸张抄造过程的多变量系统转变为单变量系统，实现纸张定量、水分之间的解耦，具有解耦效果好、鲁棒性强的优点。

[1]YOUBin,PENGHan,HUMu-yi,etal.DesignoftheBasisweightandMoisturecontentdecompositioncouplingcontrolsystembasedonRBFneuralnetwork[J].TransactionsofChinaPulp&Paper, 2012, 4(27)： 39. 尤 斌, 彭 晗, 胡慕伊, 等. 基于RBF神经网络的纸张定量水分解耦控制系统设计[J]. 中国造纸学报, 2012, 4(27)： 39.

[2]TANGWei,PANGXiao,WANGQi,etal.Acontrolschemeofdomestichighspeedpapermachineflowsystem[J].ChinaPulp&Paper, 2015, 8(34)： 49. 汤 伟, 庞 肖, 王 琦, 等. 一种国产高速卫生纸机流送系统控制方案[J]. 中国造纸, 2015, 8(34)： 49.

[3]LIMing-hui,HUYa-nan.RealizationofvariablefrequencyconstantpressurewatersupplysystembasedonFUZZY-PIDcontrolinpapermakingenterprise[J].PaperandPaperMaking, 2015, 5(34)： 16. 李明辉, 胡亚南. 基于FUZZY-PID控制的变频恒压供水系统在造纸企业中的实现[J]. 纸和造纸, 2015, 5(34)： 16.

[4]ZHAOQian-mei,CHENShuai-shuai,HUMu-yi.TheExpert-fuzzyPIDControlSystemofPulpConcentration[J].ChinaPulp&Paper, 2015, 12(34)： 53. 赵倩梅, 陈帅帅, 胡慕伊, 等. 纸浆浓度的专家-模糊PID控制系统[J]. 中国造纸, 2015, 12(34)： 53.

[5]LIMing-hui,LIYan.DecouplingandTime-delayControlStrategyofBasisWeightandMoistureContentMeasureinPapermaking[J].TransactionsofChinaPulp&Paper, 2007, 4(22)： 92. 李明辉, 李 艳. 纸张定量水分解耦及滞后控制策略的研究[J]. 中国造纸学报, 2007, 4(22)： 92.

[6]LIUWen-hua.TheAanlysisandApplicationofDecouplingControlforAircushionHeadBox[J].ChinaPulp&Paper, 2016, 6(35)： 60. 刘文华. 气垫式流浆箱解耦控制的分析及应用[J]. 中国造纸, 2016, 6(35)： 60.

[7]ZhangJ,ZhouJG,LiWX.PIDneuralnetworkfordecouplingcontrolofmulti-inputandmulti-outputsystem[J].JournalofHarbinEngineeringUniversity, 2000, 21(5): 6 (inChinese).

[8]BAIChen,FANYao.AdaptivedecouplingcontrolofMIMOsystembasedonFuzzyNeuralNetwork[J].JournalofBeijingUniversityofAeronauticsandAstronautics, 2015, 11(41)： 2131. 白 辰, 樊 垚. 基于模糊神经网络的MIMO系统自适应解耦控制[J]. 北京航空航天大学学报, 2015, 11(41)： 2131.

[9]LIULing-long,LIUXue-feng,ZHOUXi-long.DecouplingmethodofmultivariablesystembasedonFuzzyNeuralNetwork[J].JournalofOceanUniversityofChina, 2013, 2(43)： 99. 刘珑龙, 刘雪锋, 周西龙. 基于模糊神经网络的多变量系统的解耦方法[J]. 中国海洋大学学报, 2013, 2(43)： 99.

[10]ZhangW,QiaoJF,LiFJ.Directadaptivedynamicneuralnetworkcontrolfordissolvedoxygenconcentration[J].ControlTheory&Applications, 2015, 32(1): 115.

[11]ZHANGAi-juan,HUMu-yi,HUANGYa-nan,etal.ApplicationoffuzzyPIDbasedonexpertcoordinationlevelinpHvaluecascadecontrolloop[J].ChinaPulp&Paper, 2016, 7(35)：44. 张爱娟, 胡慕伊, 黄亚南, 等. 基于专家协调级的模糊PID在PH值串级控制回路中的应用[J]. 中国造纸, 2016, 7(35)：44.

(责任编辑：常 青)

Research and Application of Basis Weight and Moisture Content Control Strategy Based on FNN Decoupling

HU Ya-nan1MA Wen-ming1,*WANG Meng-xiao2

(1. Xijing University, Xi’an, Shaanxi Province, 710021; 2.Shaanxi Xiwei Aotumation Control Engineering Limited, Xi’an, Shaanxi Province, 712000)(*E-mail: 987746606@qq.com)

Aiming at the problem of strong coupling between paper basis weight and moisture content in the paper making process, a decoupling controller based on fuzzy neural network (FNN) was proposed. Firstly, coupling compensation of control system was implemented using fuzzy control. Secondly, the neural network was used to optimize the fuzzy control rules and the decoupling compensation parameters in the control process. The multivariable system of paper making process was transformed into a single variable system, which could realize the decoupling between the paper basis weight and moisture content. The simulation results showed that the FNN decoupling controller had better dynamic response and stronger robustness. The strategy was successfully applied to the production of a paper mill in Zhejiang province by the Shaanxi XiWei Aotumation Control Engineering Limited. The basis weight control accuracy was about 3.9 g/m2, and the water content control precision was about 1%, which met the high precision control requirement of the paper machine.

basis weight; moisture content; fuzzy control; neural network; FNN

胡亚南先生，硕士，助教；主要研究方向：智能控制及工业过程高级控制与应用。

2017- 03- 06(修改稿)

陕西省科技研究发展(攻关)项目(2013K07-28)。

TS736+.3

A

10.11980/j.issn.0254- 508X.2017.07.009

*通信作者：马文明，硕士，助教；主要研究方向：电力电子与电力传动、电机控股与变频调整。