基于集对联系熵的三支决策模型及应用
2017-08-07李丽红刘保相
李 言, 李丽红, 李 爽, 白 斌, 刘保相
(华北理工大学 理学院 河北 唐山 063000)
基于集对联系熵的三支决策模型及应用
李 言, 李丽红, 李 爽, 白 斌, 刘保相
(华北理工大学 理学院 河北 唐山 063000)
信息熵是信息系统中不确定性研究的有效理论工具之一.首先,构建集对联系熵建立三支决策规则,利用集对同熵、集对反熵、集对异同和异反熵对三支决策不确定性进行度量,进一步对延迟决策的风险进行分析预测.其次,考虑延迟决策的决策风险,受错判风险敏感程度、知识粒度和决策时机的影响,分析影响因素间的关系,给出延迟决策风险函数表达形式.再次,针对知识粒度的不同对进一步决策的作用不同,将集对联系熵进行改进,当集对标准集合拓展为普通集合时,出现“拒识域”,集对联系熵可进一步拓展.最后,用实例进行模型有效性验证.
三支决策; 信息熵; 集对联系熵; 延迟决策; 风险函数
0 引言
文献[1]提出了决策粗糙集,把决策域划分为正域、负域和边界域3个部分,带动了三支决策理论的发展.三支决策对应于粗糙集模型的正域、负域和边界域,从正、负域中可以分别获取接受、拒绝决策,当无法使用接受或拒绝决策时,则采用延迟决策.需要明确的是,三支决策的延迟决策不同于不作为、不决策,而是一种新的决策类型.延迟决策向确定决策的转化需要两个重要步骤:等一等的过程,需要待新的条件或信息出现,再对信息深入分析,使决策倾向性更加明朗;做出决策.
国内外学者对延迟决策域的处理进行了多方面的探索,现有的研究主要集中在三支决策分类阈值的确定、不承诺代价敏感分类及边界域样本处理等方面.文献[2-3]提出了三支决策分类阈值的自适应算法和模拟退火算法,并将其应用于垃圾邮件过滤问题.文献[4]提出基于构造性覆盖算法的三支决策阈值确定方法和边界域样本处理方法.文献[5]研究了代价敏感三支决策模型,并将其应用于人脸识别问题.文献[6]讨论了三支决策阈值的系数确定方法.
随着三支决策理论在多领域中的应用,三支决策的延迟决策需付出的代价与决策风险引起学者们的关注.文献[7-10]将集对分析方法与三支决策理论结合,指出了三支决策、粗糙集和集对在形式上的统一性,给出了三支决策的集对分析数学模型,并给出三支决策集对分析模型中决策正确性的可靠程度.当同异反联系函数中的参数b为0时,三支决策转化为二支决策问题,是三支决策理论的扩展和三支决策应用的新途径.本文进一步构建集对联系熵作为三支决策不确定性的度量,用以对决策方案信息进行刻画,对延迟决策的风险进行分析预测,并通过实例证明了模型的正确性和可操作性.
1 相关理论
1.1 三支决策
三支决策理论的基本思想是在实体评价函数上引入两个阈值,并构造所需要的三个域.设U是有限、非空实体集或者决策方案集,C是有限条件集,条件集可能包含指标、目标或约束.决策任务是基于给定条件对每一个实体x∈U做出相应决策.条件集C给出了决策的依据,通过构造评价函数给出决策.当信息不确定或者不完整时,可能无法确定实体是否满足条件,也就是评价函数是对实体满足条件的一种估计而非精确值,由于这种估计的不确定性,采用二值决策可能比较困难,在评价函数值既不很高也不很低时,不论是接受或拒绝都显得不合理.此时引入三支决策,给定阈值α和β:
1) 当评价函数值大于或等于α时,接受该实体.
2) 当评价函数值小于或等于β时,拒绝该实体.
3) 当评价函数值在α和β之间时,既不拒绝也不接受,选择不承诺决策.
构成的3个两两不相交的域,分别记为正域(POS)、负域(NEG)和边界域(BND).粗糙集是典型的三支决策模型,粗糙集模型的正域、负域和边界域可以解释为接受、拒绝和不承诺3种决策的结果.
1.2 三支决策的集对分析模型
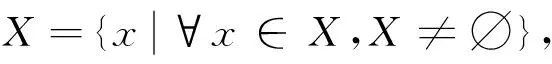
定义2[8]将集对中的集合Y看作评价标准集合,根据∀x∈X,y∈Y. 有关系R、无关系R以及不确定有无关系R,称序偶子集:
为集合X与Y在问题W下的同一性、对立性和不确定性序偶集.并将
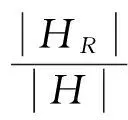
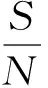
u(X,Y)=a+bi+cj,
(1)
其中:a,b,c∈[0,1],且有a+b+c=1.
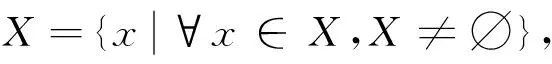
将同异反联系度函数u(X,Y)=a+bi+cj作为评价函数(此时的i和j仅具有符号含义而不进行赋值),根据决策最小风险原则,三支决策的三个域定义为:
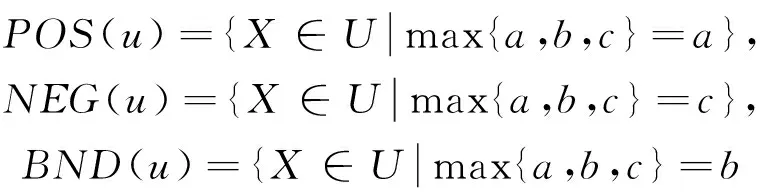
}.
据此构造的三支决策规则为:当x∈POS(u),做出接受决策;当x∈NEG(u),做出拒绝决策;当x∈BND(u),做出不承诺决策.
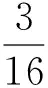
为了同时凸显同异反联系状态和知识粒度在三支决策中的作用,有必要引入集对联系熵来度量三支决策不确定性,从而对延迟决策结果进行预判,进一步控制三支决策风险.
图1 决策示意图Fig.1 Decision-making dagram
图2 决策示意图Fig.2 Decision-making dagram
2 基于集对联系熵的三支决策
三支决策的研究源于问题的不确定性,熵是系统不确定性的度量.随着对粗糙集理论研究的深入,信息熵被陆续引入到粗糙集研究中.文献[11]讨论了知识粗糙性和信息熵的关系,证明了熵与互信息对于定义在知识上的偏序“较细”都是单调下降的.文献[12]指出粗糙熵和模糊熵随知识粒度的变化规律不一定符合人们的认知规律,从信息熵角度提出了一种粗糙集不确定性的度量方法.文献[13]提出一种基于粗糙集和信息熵的属性约简算法.以上研究表明,熵作为不确定性的度量,很适合作为三支决策信息度量与刻画的运算工具[14-17].集对联系熵的构建则可以系统展示三支决策的不确定状态.
2.1 集对联系熵的构建
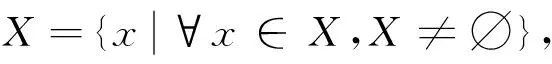
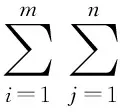
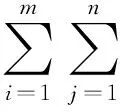
为三支决策问题的集对同熵和集对反熵,其中:
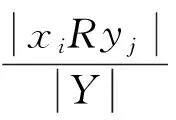
称
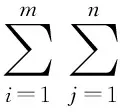
(2)
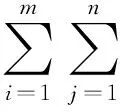
(3)
为三支决策的集对异同熵和集对异反熵,其中pi为第i个知识“属于”Y的可靠程度,称
SH(X,Y)=HP(X,Y)+(HB1(X,Y)+HB2(X,Y))i+HN(X,Y)j
(4)
为三支决策的集对联系熵.其中HB(X,Y)=HB1(X,Y)+HB2(X,Y),由式(2)和(3)给出,即集对异同熵和集对异反熵之和又称为集对差异熵.
给定三支决策问题,集对联系熵的基本性质如下:
性质1HP(X,Y)≥0,HN(X,Y)≥0,HB1(X,Y)≥0,HB2(X,Y)≥0均成立,即集对同熵、集对反熵、集对异同熵和集对异反熵均满足非负性.(证明略)
性质2 当S/N=1或P/N=1时,集对同熵、集对反熵、集对异同熵和集对异反熵均为0,则此时的三支决策为确定性决策.
集对联系熵作为一个整体,由于参数i、j的取值变化,会相应发生变化.当j取-1时,如果集对联系熵仅剩余包含i的部分,集对同熵和集对异熵相等,此时整体决策不确定性最大.
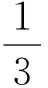
j.
借助集对联系熵,可直观看到,两个问题的集对同熵和反熵相同,此时整体决策不确定性最大,问题1的集对异同熵小于异反熵,说明问题1的延迟决策结果倾向拒绝决策更加合理,问题2的集对异同熵大于异反熵,说明问题2的延迟决策结果倾向接受决策更加合理.
2.2 三支决策规则
以集对联系熵为决策度量函数,可以构造三支决策规则(此时的i和j仅具有符号含义而不进行赋值),三支决策的3个域定义为:
决策正域中是决策为“接受”的相应结果,此时的风险小于划分为决策负域或边界域的风险;决策负域中是决策为“拒绝”的相应结果,此时的风险小于划分为决策正域或边界域的风险;边界域中是“不承诺”的相应结果,此时的风险小于划分为决策正域或负域的风险.
进一步地,HP(X,Y)=HN(X,Y)时,HB1(X,Y)>HB2(X,Y),提示延迟决策有向接受决策的倾向;HB1(X,Y) 基于集对联系熵构造的三支决策准确率为: 正确接受率为 错误接受率为 正确拒绝率为 错误拒绝率为 对三支决策接受域、拒绝域的风险评价可以归结为确定性风险评价问题,延迟决策域的风险评价则不同,如何先期预测延迟决策这一待选择状态的后期风险是三支决策应用中不可逾越的根本问题.经初步分析给出延迟决策的风险R(B)的影响因素. 1) 延迟决策风险影响因素 ① 受拒绝决策和接受决策的风险影响,将本应做出接受决策做出了拒绝决策,或者本应做出拒绝决策却做出了接受决策,决策风险是不同的,因此延迟决策的风险受错判风险敏感度影响, R(B)∝max(λPN,λNP). 其中:λPN是本应做出接受决策却做出拒绝决策的代价;λNP为本应做出拒绝决策却做出接受决策所要付出的代价.即决策风险更依赖于对错判风险更敏感的一方. ② 延迟决策的风险与下次决策的时机有关,也就是与“等一等再决策”的时间长短有关,若没有利用好“等一等”的机会,急于做出接受或拒绝决策,有可能增加错误接受率或错误拒绝率.若时间过长,错过了决策时机,可能会使做出的决策失去意义,因此延迟决策的风险受不承诺周期时间影响, minR(B)=R(B)tD,t∈(t0,tD),R(B)单减;t∈(tD,t1),R(B)单增. ③ 随着学习和对事物的进一步认识,会使支持接受决策或拒绝决策的属性特征增加,决策风险会发生改变,因此延迟决策的风险是独立属性个数的函数R(B)∝δ(x),δ(x)为变化的独立属性个数. 2) 各影响因素间的关系 3个影响因素并非相互独立,而一定程度上是相关联的,独立属性个数受决策时机影响,错判风险又与独立属性有关.将错判风险和独立属性影响作为主要因素,决策时机为限制条件,构造3个主要影响因素间的多元函数,对延迟决策风险进行描述: R(B)ti=f(max(λPN,λNP),δ(x)), 其中:ti为第i个能够做决定的时刻,当ρ的取值趋于1时,说明ti+1时刻与ti时刻的决策结果趋于稳定,此时的延迟决策可以向二支决策转化. 1) 正同熵和负反熵为确定的值,构造的接受和拒绝域也是确定的.但是,边界域部分由于决策标准集的含义不同,每一个边界域的知识可能表示一个不同的领域,如大小、颜色,因此边界域每一个知识都有一个隶属程度p,此时的三支决策评价函数为 SH(X,Y)=HP(X,Y)+(HB1(X,Y)+HB2(X,Y))i+HN(X,Y)j, 其中: 图3 决策示意图Fig.3 Decision-making dagram HP(X,Y)、HN(X,Y)计算同上. 2) 把评价标准集拓展为普通集合如图3所示. 决策问题中便存在了“拒识域”[12],即图中的“#”域部分,此时的拒识域不能简单归为不确定域,因为随着延迟决策的知识粒化和搜索,拒识域的粒度不变,此时的决策风险也未知,可以作为一种新的决策类型处理,此时基于集对联系熵的评价函数定义为: 其中: PZ为拒识域与全集U的占比. 小A决定购买一套商品房,他目前的购房能力如下:可用于购房的资金为30万元,家庭月收入9 000元,并且以每年10%速度稳定增长.在做出最终的决定之前,他收集了大量关于房屋购买相关信息的建议,在最终决定是否采纳这些建议之前,希望可以通过这些信息的整合,以最终决定是否购买及购买房屋的位置.提取条件属性中的部分属性作为示例进行分析,选择的属性有房屋位置与工作单位距离(a1)、房屋楼层是否符合要求(a2)、环境配套接受程度(a3)、价格接受程度(a4).对应决策属性为是否值得购买(d).以某小区为例进行分析,其决策形式背景如表1所示. 则此小区的购买意向的同异反联系度为 集对同势和集对反势相等[8],消费者处于买和不买的犹豫状态,此时做出的决策必然是“暂时不买房”,即采取三支决策的延迟决策. 表1 决策形式背景 进一步对延迟决策进行再决策,对4个评价因素进行排序,选取Z={x1,x4,x6,x8},计算各属性与决策结果的同异反联系函数: 由集对势和决策结果之间的关系,得出四个属性的排序为:a4>a2>a3>a1.即买房决策中,价格因素是考虑最多,其次是楼层、小区环境和距离因素.对价格因素和距离因素进行心理评估,x2与x6接受程度为0.7,因此取p=0.7,计算集对联系熵: HB1(X,Y)>HB2(X,Y). 集对异同熵大于集对异反熵,根据三支决策规则,此时延迟决策应作出“接受域”的结果,即“买房决策”. 接下来考虑决策时机、决策粒度、错判风险敏感度因素,对延迟决策结果进行风险评估. 决策粒度分为价格上涨趋势和收入上涨趋势两方面去评价,结合2016上半年的经济增长形式,该地房价稳中有升,平均每月环比上涨0.3%,然而消费者的工资收入年均环比上涨10%,工资上涨增幅小于房价上涨增幅,R(B)随δ(x)变细而上升. 错判风险敏感度主要指在应该买的时候做出“不买”的决策,可能失去最好的价格优势.在不该买的时候做出“买”的决策,也可能承担很多利息的同时套牢了资金,结合其经济基础,房贷支出占家庭总收入的比例不大,因此λPN>λNP. 综合二者,f(max(λPN,λNP),δ(x))随变量变化呈现综合上涨的趋势,ρ也随之增大,因此延迟决策的时间越早、且选择接受结果即“买房”的决策风险更小. 本文将集对方法与三支决策相融合,定义了集对联系熵统一刻画三支决策的不确定风险,并初步探讨了延迟决策的风险相关因素,同时根据知识粒度对决策的影响,给出了集对联系熵的拓展方法.随着延迟决策的进行,决策接受域和拒绝域会发生变化,需持续进行三支决策,并通过适当设立时间阈值的方式,得到理想的决策结果.对风险函数的合理量化是下一步的研究目标. [1] YAO Y Y.Three-way decisions with probabilistic rough sets[J].Information sciences,2010,180(3):341-353. [2] 贾修一,李伟湋,商琳,等.一种自适应求三支决策中决策阈值的算法[J].电子学报,2011,39(11):2520-2525. [3] 贾修一,商琳.一种求三支决策阈值的模拟退火算法[C]//第十二届中国Rough集与软计算学术会议、第六届中国Web智能学术研讨会及第六届中国粒计算学术研讨会联合学术会议.合肥,2012:2603-2606. [4] 张燕平,邹慧锦,赵姝.基于CCA的代价敏感三支决策模型[J].南京大学学报(自然科学版),2015,51(2):447-452. [5] 张里博,李华雄,周献中,等.人脸识别中的多粒度代价敏感三支决策[J].山东大学学报(理学版),2014,49(8):48-57. [6] ZHANG Y,YAO J T.Determining three-way decision regions with Gini coefficients [M].Germany West Berlin: Springer International Publishing,2014. [7] 刘保相.粗糙集对分析理论与决策模型[M].北京:科学出版社,2010. [8] LI L H,LI Y,SUN J,et al.Application of set pair analysis in three-way decisions [J].Journal of chemical and pharmaceutical research,2015,7(3):1170-1175. [9] 李丽红,李言,刘保相.三支决策中非承诺型决策的转化代价与风险控制[J].计算机科学,2016,43(1):77-79. [10]刘保相,白斌,李丽红,等.集对属性软计算方法及应用[J].计算机科学,2016,43(1):69-72. [11]苗夺谦,王珏.粗糙集理论中知识粗糙性与信息熵关系的讨论[J].模式识别与人工智能,1998,11(1):34-40. [12]王国胤,张清华.不同知识粒度下粗糙集的不确定性研究[J].计算机学报,2008,31(9):1588-1598. [13]吴尚智,苟平章.粗糙集和信息熵的属性约简算法及应用[J].计算机工程,2011,37(7):56-58. [14]HU B Q.Three-way decisions space and three-way decisions[J].Information sciences,2014,281:21-52. [15]薛占熬,袁艺林,辛现伟,等.多粒度广义L-模糊可变精度粗糙集[J].郑州大学学报(理学版),2016,48(3):82-89. [16]梁吉业,孟晓伟.信息熵在粗糙集理论中的应用[J].山西大学学报(自然科学版),2002,25(3):281-284. [17]黄兵,何新,周献中.基于广义粗集覆盖约简的粗糙熵[J].软件学报,2004,2:215-220. (责任编辑:方惠敏) Three-way Decisions Model and Application Based on Set Pair Information Entropy LI Yan, LI Lihong, LI Shuang, BAI Bin, LIU Baoxiang (CollegeofScience,NorthChinaUniversityofScienceandTechnology,Tangshan063000,China) Information entropy was an effective theory on uncertainty research in information system. Firstly, a set pair of information entropy should be constructed to establish three-way decision rules. The uncertainties of three-way decision rules were measured by the similar-entropy, anti-entropy, and different-entropy. Then prediction risks of delay decisions needed to be analyzed and predicated further. Secondly, in view of decision-making risks of delayed decision-making, which was influenced by the miscarriage risk sensitivity, knowledge of particle size and the timing of decisions, the function formula of delayed decision-making risks could be given through the analysis of relationship between the influencing factors. Furthermore, different knowledge size played different role in further decision-making. The set pair information entropy could be improved. When standard set expanded to general collection, a new domain “rejection domain” appeared. The set pair information entropy could be improved further. Finally, an instance was applied to verify the validity of the model. three-way decisions; information entropy; set pair information entropy; delay decision; risk function 2017-04-05 国家自然科学基金项目(61370168);河北省自然科学基金项目(E2017209178);华北理工大学青年科学基金项目(Z201517). 李言(1990—),女,河北晋州人,助教,主要从事粗糙集、三支决策等方面的研究,Email:danliyan@163.com. TP399 A 1671-6841(2017)03-0052-07 10.13705/j.issn.1671-6841.2017070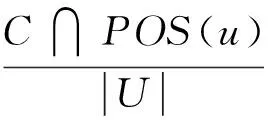
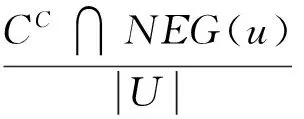
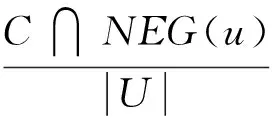
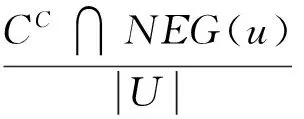
3 风险分析
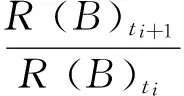
4 模型推广
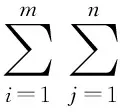

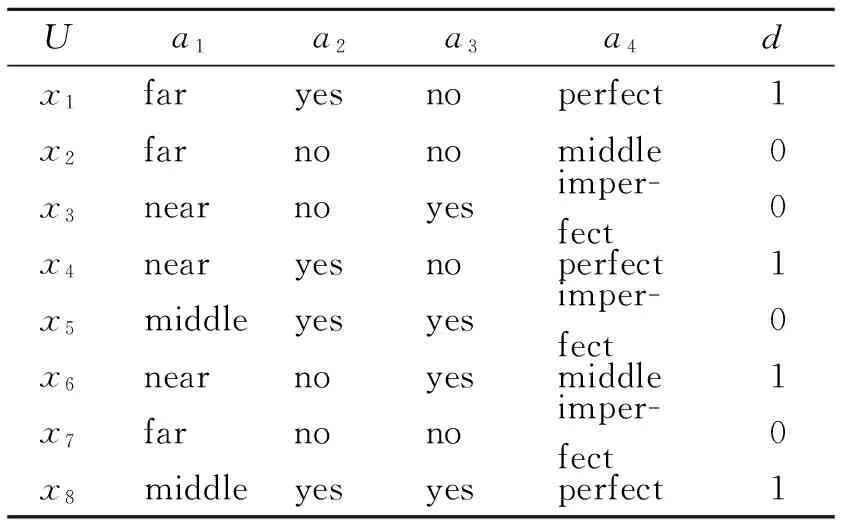
5 应用实例
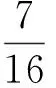
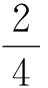
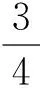

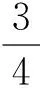
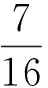
6 结束语
