基于非概率可靠性的离散变量结构优化设计

张思才，张方晓

（中国工程物理研究院总体工程研究所，四川绵阳621999）

基于非概率可靠性的离散变量结构优化设计

张思才，张方晓

（中国工程物理研究院总体工程研究所，四川绵阳621999）

目的针对工程结构设计中因材料供应规范限制使得设计变量不能连续取值以及材料性能波动、外界载荷偏差等不确定性问题，探索研究非概率可靠性在离散变量结构优化设计中的应用。方法以桁架结构杆件截面直径为设计变量、结构质量极小化为目标，考虑材料强度极限与外部载荷的不确定性，建立具有非概率可靠性指标约束的离散变量结构可靠性优化模型，并采用遗传算法求解离散变量结构优化设计问题。结果求解获得了三杆、十杆超静定桁架杆件截面直径最优组合，得到的优化结果相较确定性优化结果更具鲁棒性。结论非概率可靠性模型对于解决工程中设计变量具有离散性和不确定性的优化设计问题具有可行性。

非概率；离散变量；结构优化；可靠性

对于工程结构中材料性能波动、加工误差、外界载荷偏差等不确定性问题，早期人们通常采取安全系数法予以处理，但这种方法往往取决于设计者的工程经验与认识。随后，诸多学者将不确定性参数视为随机变量，发展了基于应力-强度干涉模型的结构可靠性优化设计方法，然而概率可靠性对概率模型参数非常敏感[1]，参数较小的误差都可能引起结构可靠性出现较大的偏差。在实际工程中得到足够的信息来确定变量的概率分布基本上不现实的，获得其不确定界限却相对容易。Ben-Haim[2]基于凸集理论提出了非概率稳健可靠性模型，以系统容许的不确定性最大化来评价其可靠性，该方法在含有不确定性因素的结构或系统可靠性分析评估中得以应用[3—6]。郭书祥[7—8]等提出了基于区间模型非概率可靠性模型。张新峰等[10]对基于区间的、基于凸集理论的两种可靠性模型指标进行了对比分析，研究表明，基于区间的可靠性模型指标更偏保守。目前，非概率可靠性模型多用于不确定性系统或结构的可靠性指标求解或分析，而非概率可靠性优化设计相关报道甚少，且多应用于求解连续变量结构优化问题[11—14]。

基于区间非概率可靠性方法，考虑材料特性及外界载荷的不确定性，建立以桁架杆件截面直径为设计变量、结构质量最小为目标、具有非概率可靠性指标约束的离散变量结构优化模型，并利用遗传算法(genetic algorithms)[15]对考虑不确定性变量的三杆桁架、十杆超静定桁架结构优化问题进行求解。

1 非概率可靠性基本原理

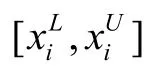
显然，η＞1时均有g(X)＞0，结构安全可靠；η＞－1时均有g(X)＜0，结构处于不安全状态；当－1≤η≤1时，g(X)＜0和g(X)＞0均有可能，此时结构可能安全，亦可能不安全。由此可见，无量纲量η的值越大，结构越安全。

2 含离散变量的非概率可靠性结构优化设计

对于离散型结构优化设计问题，可以描述为求设计变量Y=[y1,y2,…,yn]T∈RD，使：

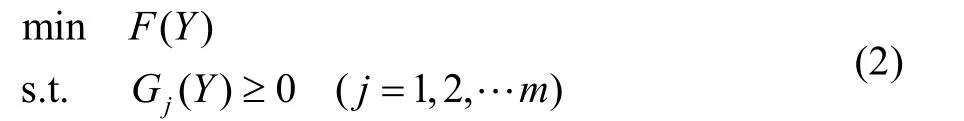
式中：Y为离散设计变量，Y=[y1,y2,…,yn]T∈RD；RD为各分量在设计空间中构成的离散空间；n为设计变量个数；m为约束条件数量；F(Y)为目标函数；G(Y)为约束函数。

以离散取值的结构件截面直径为设计变量、系统质量最小化为目标，研究考虑材料强度极限或许用应力和外载荷等参量存在不确定性的结构优化问题。显然，材料强度极限和外载荷的不确定性仅对约束函数产生影响，则将式(2)优化问题表达为：

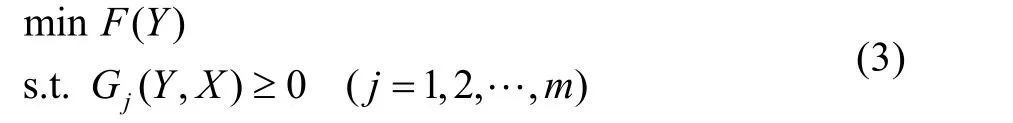
式中：X=[x1,x2]T，x1，x2分别表示材料强度极限和外载荷。

依照非概率可靠性基本原理，可以得到基于非概率可靠性的离散变量结构优化设计模型。即求设计变量Y=[y1,y2,…,yn]T∈RD，使：

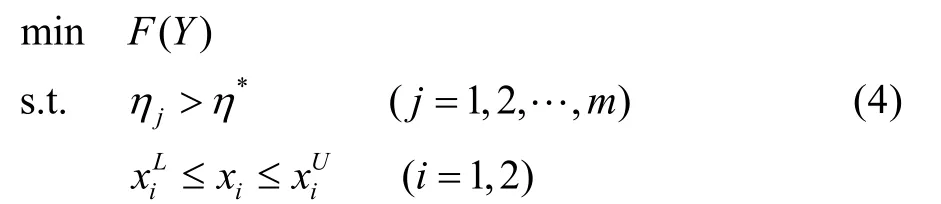
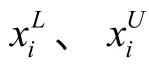
利用基于二进制编码的遗传算法对此优化问题进行求解。对于遗传算法中每一代群体，根据材料强度极限和外载荷的上、下边界，可以获得各个体在功能函数G(Y,X)状态下的最大值Mmax和最小值Mmin，进而得到其均值与离差，通过式(1)可以计算得到各个体对应的结构非概率可靠度，然后将此可靠度与可接受的可靠性指标要求对比，并通过罚函数法将其差异引入遗传算法中的适应度计算，以评判其优劣以及寻优。

3 算例

3.1 三杆桁架结构优化

以文献[16]给定的三杆桁架结构优化问题为基础，将杆件材料的许用应力及外界载荷相对名义值存有10%的扰动考虑。

利用遗传算法并将其群体规模设为80，最大迭代次数为100，交叉率为0.99，变异率为0.01进行优化求解。在η*取1.0～1.2时，遗传算法求解得到的最佳个体均为0111，1111，分别对应A1=A3=2.54 cm2，A2=4.4 cm2，目标函数最优值为F=16.01 kg。确定性模型和非概率模型的优化结果见表1，可以看出，非概率可靠性优化模型得到的目标函数值大于确定性优化模型。表明考虑不确定性参数影响时，须增加桁架杆件截面直径（杆件1、3，杆件2未变化）方可满足结构可靠性需求。杆件截面直径优化结果及目标函数并未随着可靠性指标的提高而有所变化，这表明将杆件1，3截面直径增大至一定程度后，即可满足较高的可靠性指标要求，使设计者更易权衡此类结构的可靠性与经济性。

表1 三杆优化结果

3.2 十杆桁架结构优化

十杆桁架结构（圆柱形实心杆件）如图1所示。已知P=10 kN，[σ+]=[σ－]=100 MPa，密度ρ=7.8×103kg/m3，a=b=1.0 m。以各杆横截面直径(mm)为设计变量，其取值集合为{6.00，6.75，6.81，7.46，7.69，8.19，8.51，8.67，9.20，9.37，9.91，10.38，10.53，10.99，11.69，12.71}，材料许用应力和外界载荷按相对名义值有10%的扰动考虑。以结构质量最轻为优化目标，许用应力为约束条件。遗传算法的群体规模设为150，最大迭代次数为200，交叉率为0.99，变异率为0.01。考虑确定性模型、不同可靠性指标要求的非概率模型下十杆桁架结构优化结果见表2。

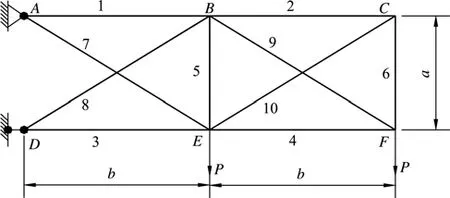
图1 十杆桁架结构

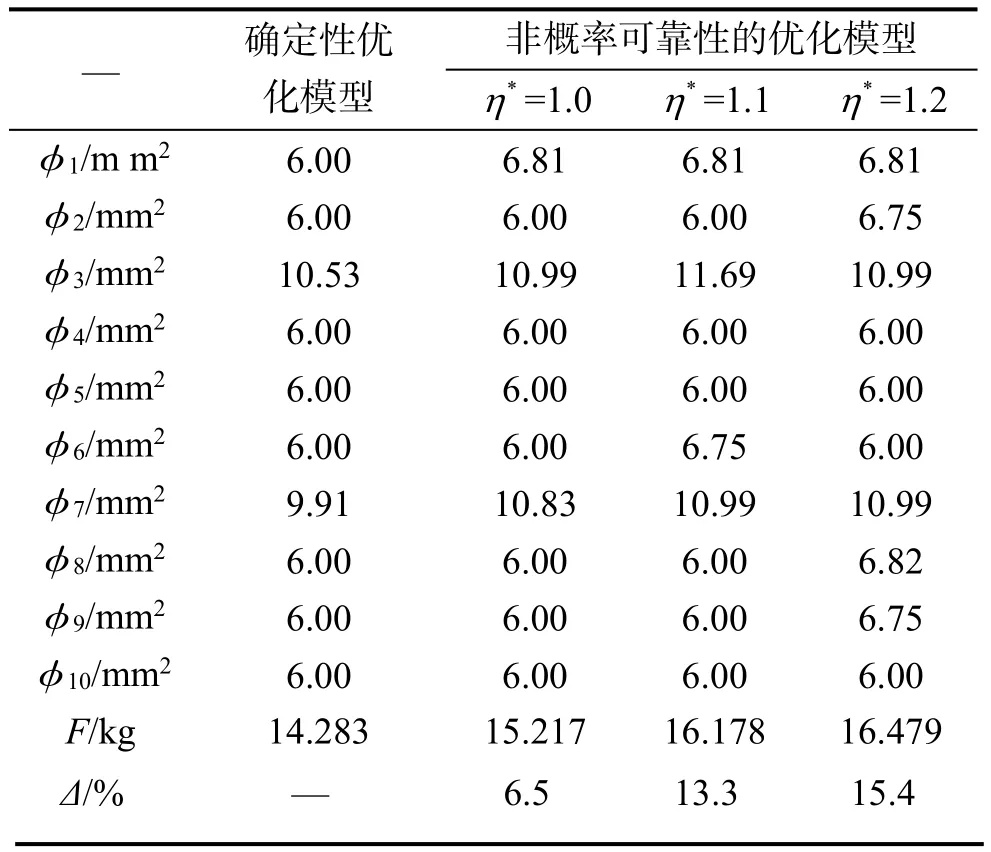
表2 十杆桁架优化结果

从表2中可以看出，不同可靠性指标要求下的非概率可靠性优化模型获得的目标函数值均大于确定性优化模型，且随着可靠性指标要求的提高而逐渐增大。表明可靠性约束条件与目标函数性能是相互矛盾的，必须通过增大杆件截面直径（即目标函数性能下降）解决某些设计参数不确定性带来的不利影响，从而达到预期的可靠性指标要求。因而需设计者综合各方因素权衡此类结构的可靠性与经济性，尤其对于不能连续取值的离散变量结构优化问题，其取值可能使目标函数性能下降更为明显。

4 结语

针对含有离散变量及不确定因素的工程问题，以常见的超静定桁架结构优化为例，考虑影响结构性能的材料强度极限、外部载荷的不确定性，建立了具有非概率可靠性指标约束的离散变量结构可靠性优化模型并通过遗传算法求解，验证了非概率可靠性模型解决离散变量结构优化问题的可行性。计算结果表明，考虑不确定性因素获得的杆件最优组合相较确定性优化结果更具鲁棒性，设计者应权衡结构或系统的可靠性与经济性，尤其是不能连续取值的离散变量结构优化问题。

[1]ELLISHAKOFF I.Essay on Uncertainties in Elastic and Viscoelastic Structures:From A.M.Freudenthal’S Criticisms to Modern Convex Modeling[J].Computers and Structures,1995,56(6):871—895.

[2]BEN H Y.Convex Models of Uncertainty in Radial Pulse Buckling of Shells[J].Journal of Applied Mechanics, 1993,60(3):683—688.

[3]JIANG C,BI R G,LU G Y,et al.Structural Reliability Analysis Using Non-probabilistic Convex Model[J]. Computer Methods in Applied Mechanics and Engineering,2013,254:83—98.

[4]PELLISSETTI M,CAPIEZ-LERNOUT E,PRADLWARTER H,et al.Reliability Analysis of a Satellite Structure with a Parametric and a Non-parametric Probabilistic Model[J].Computer Methods in Applied Mechanics and Engineering,2008,198(2):344—357.

[5]NI Zao,QIU Zhi-ping.Hybrid Probabilistic Fuzzy and Non-probabilistic Model of Structural Reliability[J]. Computers&Industrial Engineering,2010,58(3): 463—467.

[6]MENG Zeng,ZHOU Huan-lin,LI Gang,et al.A Decoupled Approach for Non-probabilisticReliability-based Design Optimization[J].Computers and Structures,2016,175(1):65—73.

[7]郭书祥,吕震宙,冯元生.基于区间分析的结构非概率可靠性模型[J].计算力学学报,2001,18(1):56—60.

[8]郭书祥,张陵,李颖.结构非概率可靠性指标的求解方法[J].计算力学学报,2005,22(2):227—231.

[9]GUO Shu-xiang LYU Zhen-Zhou.Interval Arithmetic and Static Interval Finite Element Method[J].Applied Mathematics and Mechanics,2001,22(12):1390—1396.

[10]张新锋,赵彦,施浒立.基于凸集的结构非概率可靠性度量研究[J].机械强度,2007,29(4):589—592.

[11]GANZERLI S,PANTELIDES C P.Optimum Structural Design Via Convex Model Superposition[J].Computer Methods in Applied Mechanics and Engineering,2000, 74(6):639—647.

[12]郑灿赫,孟广伟,李锋,等.一种基于SAPSO-DE混合算法的结构非概率可靠性优化设计[J].中南大学学报(自然科学版),2015(5):1628—1634.

[13]乔心州,吕震宙.基于区间模型的结构非概率可靠性优化[J].应用力学学报,2012,29(6):682—687.

[14]杨仁.基于Bayes理论改进的系统可靠性综合MML法[J].四川兵工学报，2015(9):158—161.

[15]GOLDBERG D E.Genetic Algorithms in Search, Optimization and Machine Learning[M].MA:Addison Wesley Publishing Reading,1989.

[16]张思才,张方晓.遗传算法在离散变量结构优化设计中的应用[J].西南交通大学学报,2003,38(2):146—150.

Optimization Design of Structures with Discrete Variables Based on Non-probabilistic Reliability

Z HANG Si-cai,ZH ANG Fan g-xiao
(Institute of Systems Engineering,CAEP,Mianyang 621999,China)

ObjectiveTo explore application of non-probability reliability in optimization design of structure with the discrete variables to solve issues such as failure of continues valuing in design variables due to limit of material supply specification,fluctuation of material performance,deviation of external load,etc.MethodsThe nondeterminacy of material’s ultimate strength and external load was considered with cross-sectional diameter of trusswork rod pieces as design variable,with minimizing structural weight as target to establish a reliable optimization model for discrete variable structure of non-probability reliability index constrain.The genetic algorithm was used to solve the problems of truss optimization design with the discrete variables.ResultsOptimal combination of cross-sectional diameters of three-rod and ten-rod indeterminate truss rod pieces was obtained.The optimization result obtained was more robust than that of the deterministic optimization.ConclusionNon probabilistic reliability model is feasible for solving discreteness and non-probability in optimization design of structures with discrete variables and the uncertainty.

non-probability;discrete variables;structural optimization;reliability

10.7643/issn.1672-9242.2017.07.012

TJ02；O224

A

1672-9242(2017)07-0061-04

2017-03-15；

2017-04-21

张思才（1977—），男，四川人，硕士，高级工程师，主要研究方向为结构优化设计及算法。