数字闭环光纤陀螺死区机理研究与抑制

杨志怀,马 林,张贵材,赵晶睛

(天津航海仪器研究所,天津 300131)



数字闭环光纤陀螺死区机理研究与抑制

杨志怀,马 林,张贵材,赵晶睛

(天津航海仪器研究所,天津 300131)

在数字闭环光纤陀螺中,死区产生及其附近噪声特性恶化的主要因素可以归结于施加在相位调制器上信号的串扰。根据死区产生机理的不同,提出了偏置相位调制和阶梯波反馈调制两种死区串扰误差因素的观点。通过对这两种死区误差机理的分析和比较,提出了采用模拟相加反馈方案可以避免偏置相位调制死区误差的观点。采用速率转台法测试了光纤陀螺的死区特性,验证了理论仿真和计算的正确性。最后,通过采用三角波相位抖动抑制死区误差技术,将一种高精度光纤陀螺0.08(°)/h的死区误差抑制到0.001(°)/h以下。

数字闭环光纤陀螺;死区误差;信号串扰;死区抑制

0 引言

全数字闭环光纤陀螺具有检测灵敏度高、标度因数稳定性好、动态范围宽的特点,是中高精度光纤陀螺的主流方案。死区是闭环光纤陀螺中的一个重要课题,其表现为当光纤陀螺工作在某一低的旋转速率以下时,光纤陀螺的输出始终为零,不反映转动信号[1]。与此同时,在死区附近区域,光纤陀螺的噪声和漂移指标会明显恶化。根据光纤陀螺精度和检测系统的不同,其死区的范围可从每小时零点零几度至每小时几度,甚至更大。死区的产生主要归因于调制信号和探测器信号输出之间的电子串扰[2-6]。通过对陀螺输出施加偏置的方法可以避免小角速率下的死区[7],但是这种方法的缺点是会在陀螺输出产生附加零偏,且其受温度等环境影响。通过在反馈阶梯波前叠加一个周期性的附加调制波形(比如正弦波或三角波等)[8-9]或者一个随机调制信号[10-12]也可以抑制陀螺死区。

本文基于死区产生的机理,对信号串扰的不同作用方式及过程进行了理论分析和比较,将死区分为偏置相位调制和阶梯波反馈调制两种串扰误差。采用速率转台法,对死区抑制前后的光纤陀螺的输出特性进行了验证测试。

1 闭环光纤陀螺死区机理

闭环光纤陀螺中的死区以及死区附近区域的噪声和漂移增大,均可以归因于陀螺闭环回路中施加在相位调制器上反馈电压信号的串扰。此信号的幅值通常有几伏,而探测器被检测到的有用信号通常在微伏以下。因此当反馈信号通过电路或光路串扰进探测器输出的微弱信号时,通过信号解调会产生一个相位误差。引起反馈电压相关误差的形式主要有反馈电压与探测器输出信号之间的电子串扰耦合、光纤陀螺光路中的背向散射和偏振误差等[11]。本文将上述造成死区的反馈电压相关误差分为两类,分别称为偏置相位调制串扰误差和阶梯波反馈调制串扰误差,并分别通过建模来分析其产生死区的机理。

图1中实线部分描述了数字闭环光纤陀螺的功能框图,其中φs为光纤陀螺由转动信号产生的Sagnac相移,φF为闭环反馈阶梯波产生的相移。采用方波信号作为偏置相位调制的数字闭环光纤陀螺,通过阶梯波相位反馈技术来实现陀螺的相位零差控制,即通过反馈回路控制φF实时补偿Sagnac相移φs,使相位误差信号始终满足Δφ=φF+φs=0。

图1中的偏置相位调制串扰误差φe1,为不经历光纤陀螺光路,直接通过电路串扰的反馈电压相关误差,即是反馈电压VF中偏置方波调制信号与探测器输出信号之间的电子串扰耦合。由于串扰信号频率和陀螺解调频率相同,从而通过线路解调直接将串扰误差混合在陀螺Sagnac信号中。图1中的阶梯波反馈调制串扰误差φe2,是与反馈阶梯波直接相关的串扰误差。此串扰误差主要是由光纤陀螺光路特性或者调制信号非线性等因素造成,最终达到探测器通过线路解调直接混合在陀螺Sagnac信号中。上述两种反馈电压相关相位误差,通过光纤陀螺的闭环回路始终满足φs+φF+(φe1+φe2)=0。因此,当反馈电压相关误差能够实时准确地抵消光纤陀螺输入的Sagnac相移时,阶梯波反馈相位φF始终保持为零,此时光纤陀螺的输出不再响应输入转动信号,从而进入死区。

2 偏置相位调制串扰误差分析

偏置相位调制串扰误差主要存在于采用数字相加反馈方案的闭环光纤陀螺中,其主要归因于施加于相位调制器的反馈电压信号的2π重复复位[13]。以两态方波调制为例,驱动相位调制器的电压波形是由幅值为φb的方波偏置信号与反馈阶梯波信号叠加而成。图2 给出了闭环光纤陀螺中有无调制串扰时,施加到相位调制器上的反馈电压波形对比情况。其中,上方第1个方波信号为方波偏置调制信号,第2个信号为无串扰误差时的反馈阶梯波信号,第3个信号为无串扰误差时数字相加后的反馈电压信号,最下方的第4个信号为有串扰误差时的数字相加反馈电压信号。由于探测器输出信号的解调频率是与调制方波频率相同的,因此,当存在信号串扰时,就会产生偏置相位调制串扰死区误差。

设定串扰误差信号与偏置调制波形的幅值成正比,其比例系数称为电子串扰系数ke。电子串扰系数与所用的电子元件、PCB电路板设计、电磁兼容设计及工作频率等相关。与此同时,除了同相直接耦合外,还可能存在差分、延迟或移相耦合。如图2所示,无偏置相位调制串扰时,在非复位和复位期间的偏置调制方波幅值分别为φb和φb-2π。当存在偏置相位调制串扰时,在非复位期间,探测器上引入一个与偏置调制方波同频,幅值为φA=ke·φb的相位误差信号,其寄生在Sagnac相移φs中,使光纤陀螺解调的输出相移变为φs+φA。在复位期间,偏置调制方波的幅值变为φb-2π,此时寄生在Sagnac相移φs中的误差信号为φB=ke·(φb-2π),使光纤陀螺的解调输出相移变为φs+φB。由此可见,存在串扰耦合误差时,阶梯波非复位和复位期间的斜率均会发生变化,其对应阶梯高分别为φF=φs+φA和φF=φs+φB。因此,相对于无串扰耦合误差的理想情况而言,其复位周期也将发生变化,从而会产生光纤陀螺输出误差。当φs+φA>0且φs+φB>0(或者φs+φA<0且φs+φB<0)时,偏置相位调制串扰的存在仅仅改变了反馈电压信号的阶梯波斜率大小(符号未改变),会导致光纤陀螺输出产生误差,但是并不会产生死区,陀螺仍会反映输入转动角速度。

根据图2中描述的存在串扰误差时反馈电压信号台阶高度变化,可以计算出非复位和复位期间的持续时间tA和tB,可以分别表示为:

(1)

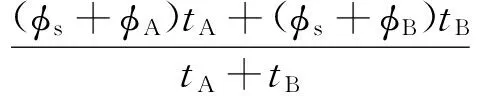
(2)

当光纤陀螺的旋转速率很小(φs很小)时,φs+φA和φs+φB的符号会不相同。其中一种情况如图3所示,φs+φA>0导致反馈电压信号在非复位期间的阶梯波斜率为正,而在复位期间由于φs+φB<0,其阶梯波斜率为负。当离开复位期间时,阶梯波台阶高度又由φs+φB<0调整为φs+φA>0,导致阶梯波斜率又变为正,直到再次达到复位期间。这样,反馈电压信号始终保持这种俘获状态,其阶梯波斜率在正负之间循环,此时光纤陀螺对角速率的变化不再敏感,即处于死区状态。

图3所示的反馈电压俘获情况下,阶梯波台阶高度复位与非复位期间的持续时间可以表示为:

(3)

其中,h=max[abs(φs+φA),abs(φs+φB)]

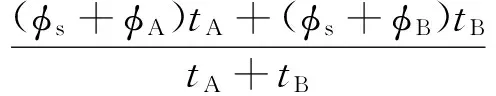
(4)

根据式(2)和式(4),可以计算光纤陀螺偏置相位调制串扰死区误差引起的死区特性,死区范围为{-φA, -φB},因此死区是对光纤陀螺的输入零速率不对称的。图4给出了采用φb=π/2的方波偏置调制时,光纤陀螺死区特性的仿真结果,死区范围大约为0.2(°)/h,其中假设电子串扰耦合系数ke=10-6,光纤环圈长3300m,平均直径0.15m。

3 阶梯波反馈调制串扰误差分析

由以上的分析可知,偏置相位调制串扰误差产生的直接原因是反馈电压的2π重复复位。由于反馈电压信号在复位期间和非复位期间的串扰误差不同,从而引起光纤陀螺反馈电压始终处于俘获状态。偏置相位调制串扰误差是采用数字相加反馈陀螺方案所特有的死区产生机理。如图5所示,当采用模拟相加反馈陀螺方案时,反馈电压信号一个周期只有一次2π复位,不存在重复复位问题。因此,偏置相位调制串扰误差始终是由固定的方波调制φb引起,其为一个恒定的电子串扰耦合误差。在这种情况下,偏置相位调制串扰误差的影响仅仅是在光纤陀螺输出中产生一个恒定的偏置,而不会引起光纤陀螺进入死区。因此，为了避免偏置相位调制串扰死区误差,建议光纤陀螺采用模拟相加反馈陀螺方案。无论采用数字还是模拟相加反馈方案,其都存在着另一种死区误差,称之为阶梯波反馈调制串扰死区误差[11]。下面着重讨论模拟相加反馈陀螺方案下的阶梯波反馈调制串扰死区误差的机理。

当存在一个阶梯波反馈调制串扰误差φe2,光纤陀螺的闭环工作方式可以描述为:

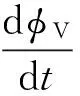
(5)

其中,φV是驱动相位调制器的反馈阶梯波信号所对应的相移,τ是光波传输光纤环圈一周所用的时间。如果在闭环反馈环路中没有相位误差,则反馈相移刚好抵消Sagnac转动相移φV=-φs·t/τ。其中φV为持续时间为τ,幅值为-φs的连续台阶构成的,如图5所示。

对于任何一种阶梯波反馈调制串扰死区误差,都可以表示为一系列的正弦误差信号。为简便起见,仅分析一次谐波相位误差分量φe=φe2·cos(b·φV+a),其中φe2是阶梯波反馈调制串扰死区误差的幅值,b为正的整数,a为相位部分。当相位误差大于Sagnac相移(α=φe2/φs>1)时,驱动相位调制器的反馈阶梯波对应的相移φV将是一个常值,可以表示为

φV=-cos-1(-1/α)/b-a/b

(6)

此时,数字阶梯波的相位台阶高度φf=0,表示光纤陀螺检测的转速为零。当相位误差小于Sagnac相移(α=φe2/φs<1)时,驱动相位调制器的反馈阶梯波对应的相位φV,会受到阶梯波反馈调制串扰误差的影响,其可以表示为[11]:

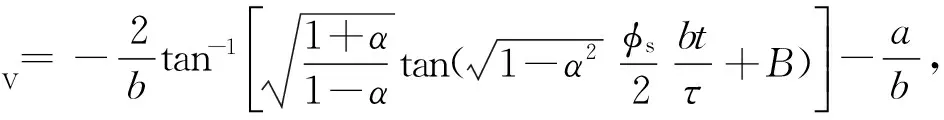
(7)

(8)

由上述分析可知,当存在阶梯波反馈调制串扰死区误差时,光纤陀螺输出的检测转速并非陀螺的真实转速,它们之间会有一个偏差因子。与此同时,由于阶梯波反馈调制串扰死区误差的存在,反馈信号φV中的相位台阶幅值φf不再是恒定的。取而代之的是,在整个2π相位范围内,相位台阶幅值是摆动的,如图6所示,实线为理想无串扰情况下的反馈阶梯波相位波形,虚线为串扰情况下的反馈阶梯波相位波形。

根据以上分析,图7给出了存在阶梯波反馈调制串扰误差时,光纤陀螺的死区特性仿真曲线,死区范围大约为0.06(°)/h,其中假设串扰幅值φe2=10-6时,光纤陀螺光纤环圈环长3300m,平均直径0.15m。可以看出,阶梯波反馈调制串扰死区误差引起的死区是对陀螺零输入角速率对称的,而偏置相位调制串扰误差引起的死区是对陀螺零输入角速率不对称的且相对较大,这是两类死区特性的区别。

4 光纤陀螺死区测试与抑制

通过以上分析可知,偏置相位调制串扰误差和阶梯波反馈调制串扰误差引起死区的机理和表现出的死区特性是不同的。偏置相位调制串扰死区是在采用数字相加反馈方案中,阶梯波的多次重复复位造成的,并且其产生的死区对于陀螺零输入转速是不对称的。阶梯波反馈调制串扰死区是各种闭环陀螺方案中均存在的,是关于陀螺零输入转速对称的。模拟相加反馈方案中,由于其反馈阶梯波不存在重复复位,可以认为其只存在阶梯波反馈调制串扰死区。此外,数字相加反馈方案中阶梯波的复位次数多,在2π电压反馈控制环路不理想情况下,会给光纤陀螺带来较大的噪声和不稳定性。这也是选择模拟相加反馈方案的原因之一。

利用速率转台法测量光纤陀螺的死区特性。通过旋转转台使光纤陀螺敏感轴扫描正东向附近,此时陀螺输出即为地球转速在陀螺敏感轴上的投影分量,从而可以获得光纤陀螺在零输出附近范围内的输出死区特性。转台的转速设置为0.001(°)/s,实测光纤陀螺的光纤环圈长为3300m,光纤环平均直径约为0.15m。图8给出了测试的陀螺死区输出特性,死区大小约为0.08(°)/h,与理论分析结果基本一致。

死区的存在会恶化光纤陀螺的阈值性能、小角速下的标度因数非线性和零偏稳定性性能。因此,必须采取一些补偿措施来抑制死区效应。抑制死区的方法有多种,一种方法是通过给光纤陀螺增加一个大的零偏偏置,将陀螺死区移开小角速率区域,从而降低死区对陀螺应用性能的影响。另一种方法是通过给光纤陀螺施加一个周期性的相位抖动信号,并且抖动信号相移φd始终满足φd+φs>φe,则光纤陀螺始终不会进入到死区[9,13-14]。再一种死区抑制方法是采用随机调制深度方案[3,10-12],随机调制技术是通过随机产生一个相位调制波形序列,使得各种电子交叉耦合包括直接耦合、延迟耦合和差分耦合在正采样和负采样上的平均值为零。

图9给出了采用三角波相位抖动抑制死区技术后,测得的光纤陀螺死区特性。可以发现陀螺在零输出附近观察不到死区。对照此光纤陀螺的百秒平滑零偏稳定性为0.001(°)/h,可以确定其死区被抑制到0.001(°)/h以下。

5 结论

本文根据数字闭环光纤陀螺中死区机理的不同,提出了偏置相位调制和阶梯波反馈调制两种串扰误差机理的观点。通过对这两种误差机理的分析和比较,提出了采用模拟相加反馈方案可以避免偏置相位调制死区误差,从而减少死区误差来源。采用速率转台法对光纤陀螺的死区特性进行了测试,验证了理论分析的正确性。最后采用三角波相位抖动抑制死区技术,将0.08(°)/h的死区抑制到0.001(°)/h以下。

[1] Lefèvre H C.The fiber-optic gyroscope [M].Boston:Artech House, 1993.

[2] Pavlath G A.Closed loop fiber optic gyros [J].Proceedings of the SPIE, 1996, 2837: 46-60.

[3] Spahlinger G, Kemmler M W, Ruf M, et al.Error compensation via signal correlation in high precision closed loop fiber optic gyros [J].Proceedings of the SPIE, 1996, 2837: 218-227.

[4] 金靖, 张春熹, 宋凝芳, 等.数字闭环光纤陀螺死区非线性机理[J].北京航空航天大学学报, 2007, 33(9):1046-1050.

[5] Chong K H, Chong K T.Analysis of deadzone error by electrical cross-coupling on a closed-loop fiber optic gyroscope [J].Journal of Institute of Control Robotics and Systems, 2014, 20(4):437-442.

[6] 宋凝芳, 李立京, 金靖, 等.光纤陀螺的死区研究[J].弹箭与制导学报, 2005, 25(1):22-26.

[7] 潘军.闭环光纤陀螺的死区现象及克服死区实验[J].航空学报, 2001, 22(2):177-179.

[8] 宋凝芳, 王夏霄, 邬战军.消除光纤陀螺死区的方法研究[J].中国惯性技术学报, 2006, 14(4):53-55.

[9] 张晓峰, 张桂才.闭环光纤陀螺中的死区抑制技术研究[J].压电与声光, 2009, 31(2):169-171.

[10] 王马华, 朱光平.基于随机共振的数字闭环光纤陀螺死区现象抑制[J].中国惯性技术学报, 2011, 19(1):100-105.

[11] Chen C J.Interferometric fiber optic gyroscope dead band suppression [J].Applided Physics Express, 2008, 1(7):119-122.

[12] 金靖, 李敏, 宋凝芳, 等.基于4态马尔可夫链的光纤陀螺随机调制[J].北京航空航天大学学报, 2008, 34(7):770-773.

[13] Grollmann P.Fiber optic Sagnac interferometer with digital phase ramp resetting US5116127 [P].1992.

[14] Matsuda H, Kawada H, Sakai K, et al.Fiber optic rotation sensing system and method for basing a feedback signal outside of a legion of instability US5020912 [P].1991.

Analysis and Suppression of Dead Band in Digital Closed-loop Fiber Optic Gyro

YANG Zhi-huai, MA Lin, ZHANG Gui-cai, ZHAO Jing-jing

(Tianjin Navigation Instrument Research Institute, Tianjin 300131, China)

In the digital closed-loop interferometric fiber optic gyro, the dead band and the increased noise result from the signal crosstalk which is applied to the phase modulator. According to the different causes, a point of view is proposed that there are two different sources causing the dead band, which are the bias modulation phase error and the step wave modulation phase error. Through the analysis and comparison of these two sources, it is proposed that there is no bias modulation phase error when using analog adding feedback method. The dead band of a fiber optic gyro is tested using the rate table, which validated the correctness of the simulation and the computation. At last a dead band of 0.08(°)/h for a high precision fiber optic gyro is suppressed under 0.001(°)/h using triangle phase jitter technique.

Digital closed-loop fiber optic gyro; Dead band error; Cross talk; Dead band suppression

2017-04-13；

2017-05-28

“十三五”装备预研项目(编号41417010102)

杨志怀(1982-),男,高级工程师, 从事光纤传感、光纤陀螺和惯性导航与控制方面的研究工作。 E-mail:yzhtj@126.com

10.19306/j.cnki.2095-8110.2017.04.015

U666.1;TN911.74

A

2095-8110(2017)04-0097-06