基于密度泛函理论的La掺杂γ-T iA l体系结构延性与电子性质∗

宋庆功 赵俊普 顾威风 甄丹丹 郭艳蕊 李泽朋

1)(中国民航大学理学院低维材料与技术研究所,天津 300300)

2)(中国民航大学中欧航空工程师学院,天津 300300)

(2016年11月9日收到;2016年12月10日收到修改稿)

基于密度泛函理论的La掺杂γ-T iA l体系结构延性与电子性质∗

宋庆功1)2)†赵俊普1)顾威风1)甄丹丹2)郭艳蕊1)李泽朋1)

1)(中国民航大学理学院低维材料与技术研究所,天津 300300)

2)(中国民航大学中欧航空工程师学院,天津 300300)

(2016年11月9日收到;2016年12月10日收到修改稿)

采用基于密度泛函理论的第一性原理方法,计算研究了La替位Ti或A l且掺杂浓度分别为1.85 at.%, 2.78 at.%,4.17 at.%,6.25 at.%,8.33 at.%,12.5 at.%的γ-TiA l合金的晶体结构、稳定性和延性等性质.结果显示,杂质La浓度x≤12.5 at.%,各个体系均具有较好的能量稳定性,即在一定条件下它们是可以实验制备的,且掺杂合金体系的密度＜4.6 g·cm−3.La掺杂引起晶格参量变化进而导致合金体系的轴比发生变化.La的低浓度(x≤6.25 at.%)掺杂使合金体系的轴比相较纯γ-TiA l更接近于1,这对于改善材料的延性极为有利,其中Ti11LaA l12体系的轴比最接近于1,预报其延性最佳.通过对比Ti11LaA l12和Ti12A l12体系的布居数、电荷密度和电子态密度,发现Ti11LaA l12体系延性改善的电子因素为:掺杂使体系内A l(Ti)原子轨道上的电子重新分布,Ti-d轨道和A l-p轨道的电子数均减小,可被p-d杂化轨道局域化的电子数减小,p-d轨道杂化键强度降低,从而使位错移动的阻力减少,延性得以明显改善.电子重新分布改变了部分化学键的性质,部分A l–Ti共价键转化为A l–La离子键,部分Ti–Ti共价键转化为Ti–La金属键,它们的共价性及方向性明显降低,材料金属性增强.在掺杂体系中A l–A l键的平均强度减弱,A l–Ti键和Ti–Ti键的平均强度增强,三者的强度差异明显减小,晶体结构的各向异性程度降低.

La掺杂γ-TiA l,晶体结构,延性,电子性质

1 引 言

TiA l合金因具有高比强度、较好的抗氧化性和抗蠕变性能以及低密度而成为航空航天、汽车发动机领域的新一代关键材料[1,2].研究表明,由γ相和α2相组成的双相TiA l合金综合性能优良,是研究开发的热点之一[3].制约该类合金材料压力加工及其应用的瓶颈是延性不足,特别是作为主要成分的γ-TiA l室温塑性较期望值仍有一定差距[3,4].为了改善该类合金材料的室温延性,研究者们进行了合金成分[5,6]、晶体结构[7,8]、组织结构[9−11]、变形亚结构[12,13]等多层次跨尺度的综合研究.研究表明,添加合金元素是改善该类合金延性的有效途径之一[14,15],例如,添加V,Cr,M n和Nb等均可改善双相TiA l合金的延性.最近,通过掺杂稀土元素来改善金属间化合物延性的方法也引起了人们的关注[16].例如,徐福松等[17]通过机械合金化制备并经退火处理得到Ti-A l-La三元合金.他们由X射线衍射及透射电子显微镜分析确认:添加微量的La可使D022结构的TiA l3在退火过程中转变为具有高对称性的L12立方结构.这将会使该合金的室温脆性得到有效抑制.Hadi等[18]实验研究表明,添加少量的La能提高Ti-43.5A l-4Nb-1Mo-0.1B合金的流变应力峰值,特别是在试样内添加0.2 at.%的La时,可使试样在900◦C和1000◦C时的流变应力峰值分别增加14%和44%.陈仕奇等[19]成功制备了成分均匀的Ti-48A l-x La合金(x=0,0.2 at.%, 0.5 at.%,1.0 at.%,1.5 at.%,2.0 at.%),并且发现,适量的La可使TiA l合金的延性提高一倍.其原因是:加入La促使基体中形成弥散的La2O3粒子,有助于降低TiA l中的氧含量,并且杂质La可使显微组织均匀细化;但过多的La会导致合金中形成粗大的氧化物粒子和气孔、合金性能恶化.事实上,关于稀土元素掺杂对TiA l合金结构与性质影响的研究刚刚开始,许多微观机理问题尚不清楚、有待探讨.例如,对Ni基合金,稀土元素能够提升其高温综合力学性能已经被证实,而对TiA l合金相关的研究报道则相对较少[16].因此,对稀土元素掺杂TiA l基合金体系的理论研究,特别是探索La与基质原子相互作用的微观机理,对于加快该类材料的研发具有重要的理论意义和技术价值.

众所周知,合金材料的性质决定于其微观结构,而微观结构与电子性质紧密相关.为了纯化稀土元素在合金体系中的作用,本文以La掺杂γ-TiA l合金系列为研究对象,在密度泛函理论基础上研究合金体系的晶体结构及其稳定性、延性(脆性)、电子性质与掺杂浓度的关联性,探索该类合金延性与电荷分布、化学键性质的内在关系.纯净的γ-TiA l属于金属间化合物,其原子间结合既有金属键特性,又有共价键特性,使其同时兼有金属的韧性及陶瓷的耐高温特性.1991年,Greenberg等[20]从电子尺度研究发现,TiA l合金中Ti原子周围电子云分布的不对称性使(0 0 1)晶面上的Ti原子之间形成的d–d共价键刚性架构,导致Peierls-Nabarro力各向异性,阻碍位错运动,增加合金产生塑性变形的难度.Moringa等[21]研究表明,TiA l晶体中存在A l-p(A l原子的3p轨道)与Ti-d(Ti原子的3d轨道)轨道杂化的方向性键合,使材料的剪切强度提高,进而造成其室温延性较差,并且通过掺杂第三元素来增强Ti–Ti键、减弱A l–Ti键,可以改善合金的延性.Eberhart等[22]认为电荷分布的各向异性是造成TiA l合金室温脆性的本质原因.最近,秦永和和乔英杰[23]通过第一性原理研究,预报La或Sm在TiA l合金中均更倾向于替代A l原子,并预测Ti8A l7La的延性优于Ti8A l8体系,但他们没有研究Ti7A l8La体系的延性,更未涉及浓度较低的La掺杂体系.关于La掺杂γ-TiA l体系的深入研究,特别是关于La与基质原子Ti和A l相互作用的微观机理,以及La掺杂的适合浓度范围等尚需深入探讨.

最近,计算模拟方法的作用再次引起材料研究者的高度关注[24].可以说,以前瞻性结构设计和性能预测为前端,以实验制备研发、性能验证为后端的新型研究范式越来越得到业界认可,这对于研发新型材料具有重要作用[25].本文关于La掺杂γ-TiA l系列合金的计算与理论研究旨在为该类合金材料的实验研究揭示微观机理、提供理论依据.

2 模型构建与计算过程

2.1 结构模型构建

纯γ-TiA l为L10型面心四方结构,空间群为P 4/mmm,其晶胞中包含2个Ti原子和2个A l原子,实验报道的晶格常量a0=b0=0.398 nm, c0=0.404 nm,α=β=γ=90◦[26],如图1(a)所示.为便于研究,将该四方结构视为由两个简单四方格子相互嵌套而成,其最小结构单元的晶格参量a1=b1=0.283 nm,c1=0.407 nm,如图1(b)所示.

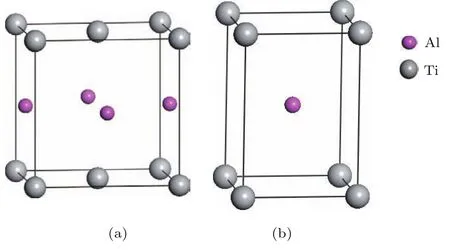
图1 (网刊彩色)γ-T iA l结构模型 (a)L10结构单胞; (b)简单四方结构单胞Fig.1.(color on line)The structuralm odels ofγ-T iA l: (a)L10unit cell;(b)sim p le tetragonal unit cell.

为了研究γ-TiA l基合金性质与杂质La浓度的关联性,在简单四方结构单元基础上构建2×2×1, 3×2×1,2×2×2,3×2×2,3×3×2和3×3×3γ-TiA l超胞,分别用一个La替代Ti原子,形成6个掺杂体系:Ti3LaA l4,Ti5LaA l6, Ti7LaA l8,Ti11LaA l12,Ti17LaA l18,Ti26LaA l27,即Ti1−xLaxA l(x=12.5 at.%,8.33 at.%,6.25 at.%, 4.17 at.%,2.78 at.%,1.85 at.%),如图2所示.同理,用一个La替代A l原子,形成6个掺杂体系TiA l1−xLax(x=12.5 at.%,8.33 at.%,6.25 at.%, 4.17 at.%,2.78 at.%,1.85 at.%).针对这12个La掺杂γ-TiA l体系研究其结构和性质,特别是化学键性质、电子性质及其影响.

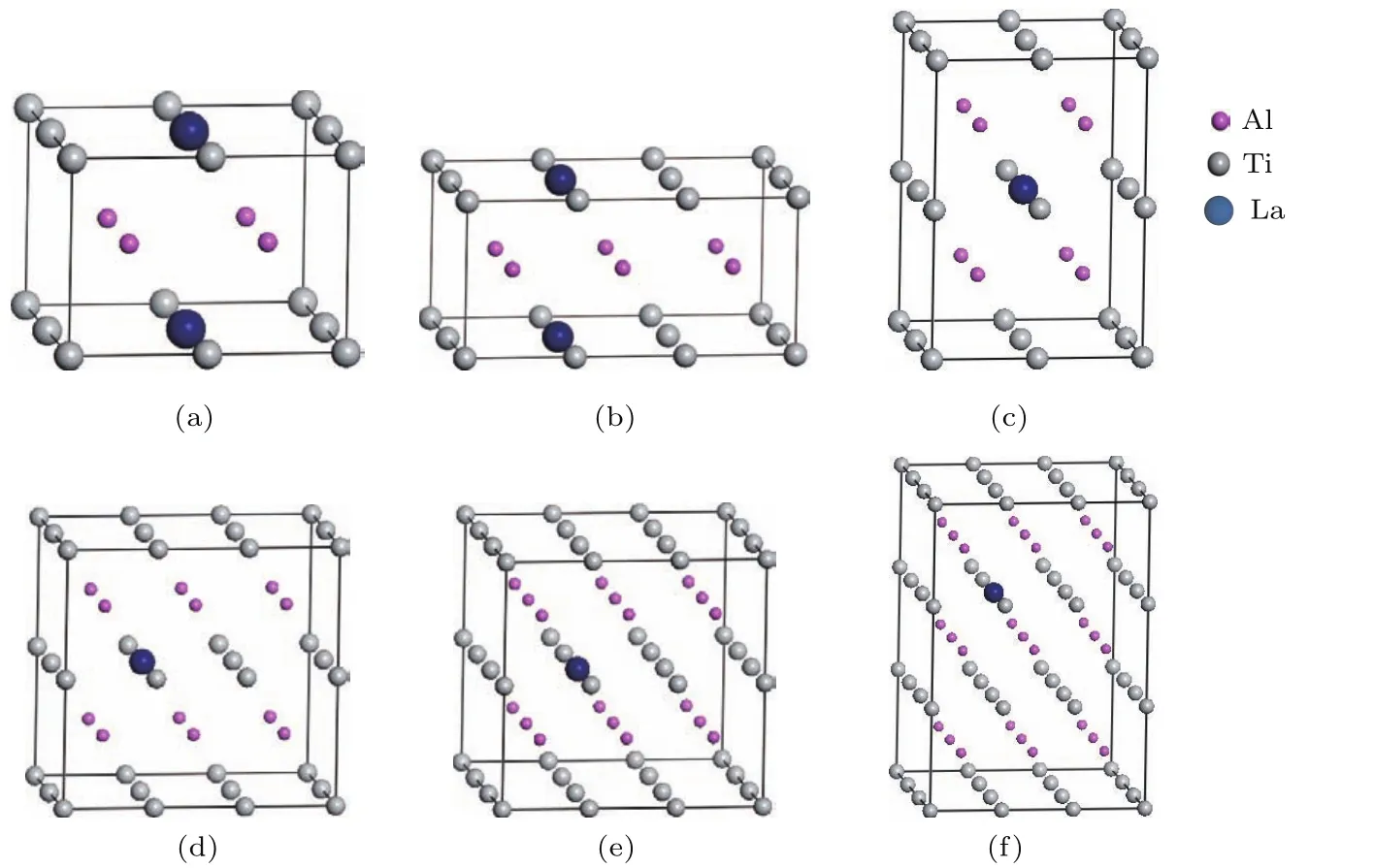
图2 (网刊彩色)掺杂γ-T iA l体系的结构模型 (a)T i3LaA l4;(b)T i5LaA l6;(c)T i7LaA l8;(d)T i11LaA l12; (e)T i17LaA l18;(f)T i26LaA l27Fig.2.(color on line)The structural m odels of La-dopedγ-TiA l system s:(a)Ti3LaA l4;(b)T i5LaA l6; (c)T i7LaA l8;(d)T i11LaA l12;(e)T i17LaA l18;(f)T i26LaA l27.

2.2 计算方法与过程

本文工作采用基于密度泛函理论的第一性原理计算方法,并结合物理与化学理论方法进行.计算方案采用平面波赝势方法,使用CASTEP(Cambridge serial total energy package)软件包,利用高性能计算集群完成计算.首先设计数种计算方案对纯γ-TiA l体系进行几何结构优化,并将优化计算结果与报道的实验结果对比,再选取相对误差较小的计算方案.本文选取晶格参量相对误差均小于1.5%的计算研究方案,具体包括:采用广义梯度近似,选取Perdew-Burke-Ernzerhof泛函为交换关联能;采用超软赝势来描述离子实与价电子之间的相互作用.原子A l,Ti和La的价电子组态分别选取为3s23p1,3s23p63d24s2和5s25p65d16s2.平面波截断能设置为350 eV,布里渊区k点分别设置为: 4×4×6(8个原子的晶胞),3×4×6(12个原子的晶胞),4×4×3(16个原子的晶胞),3×4×3(24个原子的晶胞),3×3×3(36个原子的晶胞)以及3×3×2(54个原子的晶胞).迭代计算的收敛标准为:原子能量变化量5.0×10−6eV/atom;原子相互作用力0.01 eV/nm;原子最大位移5.0×10−5nm;应力0.02 GPa.

对各个La掺杂γ-TiA l体系和纯γ-TiA l体系,均采用拟New ton算法进行几何结构优化,直至达到收敛标准.然后计算各个优化的晶体体系的结构参量、总能量、布居数、电子态密度(DOS)、电荷分布等,在此基础上进行理论分析与讨论.

3 结果与讨论

3.1 晶体的几何性质和密度

优化得到的Ti1−xLaxA l,TiA l1−xLax(x= 1.85 at.%,2.78 at.%,4.17 at.%,6.25 at.%,8.33 at.%, 12.5 at.%)体系和纯γ-TiA l体系的晶格参量、空间群和密度见表1.

表1显示,Ti11LaA l12,Ti12A l11La,Ti5LaA l6和Ti6A l5La体系的空间群为Pmmm,属于正交晶系.原因是采用的Ti12A l12(或Ti6A l6)超胞晶格参量为3a1和2b1,掺杂后体系的对称性必然发生改变.为便于对比分析,表1中已将其中各个体系的晶格参量折合成与γ-TiA l最小结构单元对应的量值.对属于正交晶系的4个体系,晶格参量b与a相对误差小于3.6%,以后均按四方晶系处理.为便于后续讨论,也将各体系的轴比R(R为L10结构的晶格参量c0与a0之比)也列于表1中.

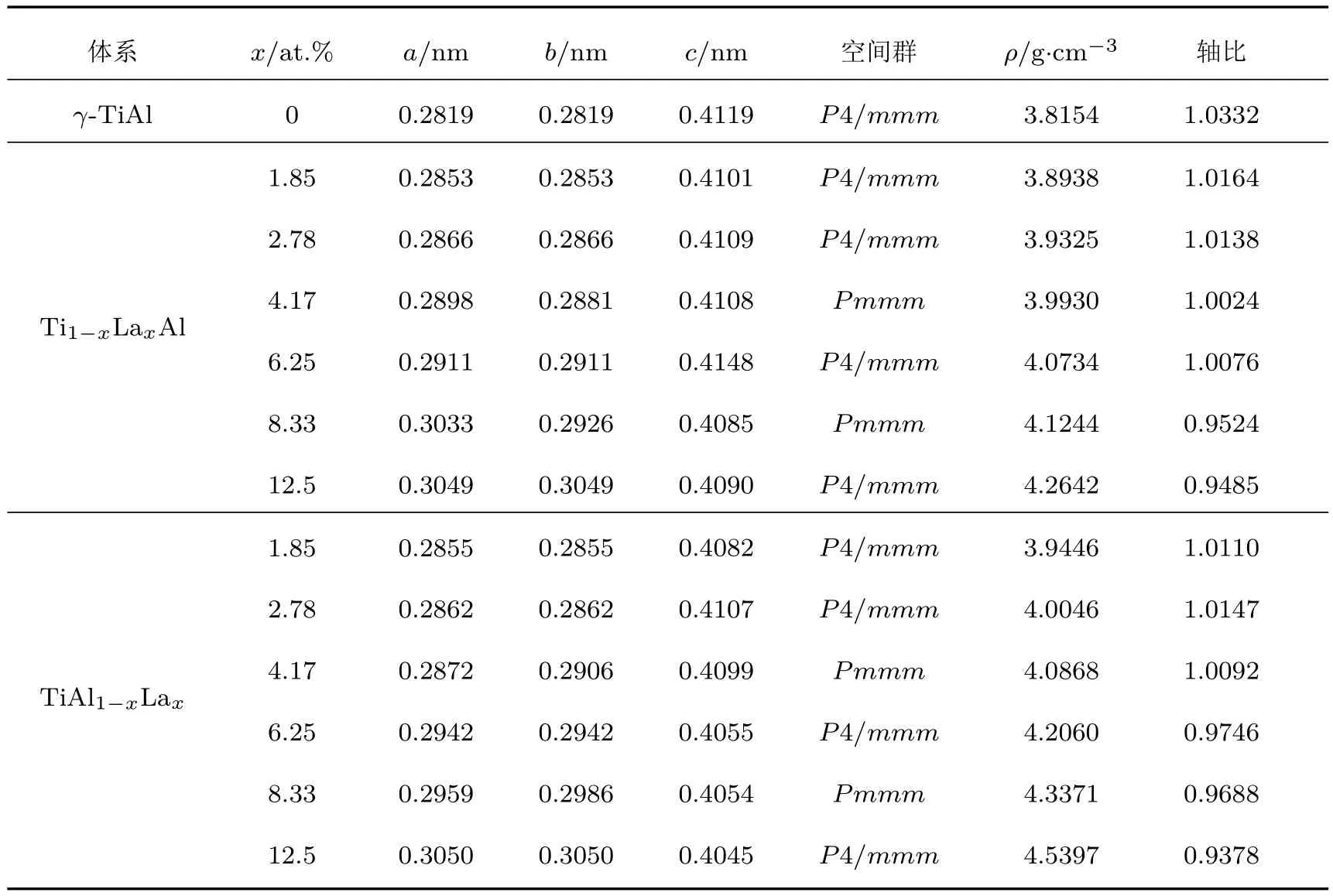
表1 La掺杂与纯γ-T iA l体系的几何性质和密度Tab le 1.The geom etrical properties and densities of La-doped and pureγ-TiA l system s.

晶格参量p与La浓度x的关系曲线如图3所示.结合图3与表1易知:对Ti1−xLaxA l和Ti-A l1−xLax两系列,晶格参量a随x变化较显著,最大增量分别为8.16%和8.19%;c随x变化较小,最大增量绝对值仅分别为0.70%和0.18%.这一现象表明,La掺杂对于调控掺杂γ-TiA l体系的轴比R极为有利.

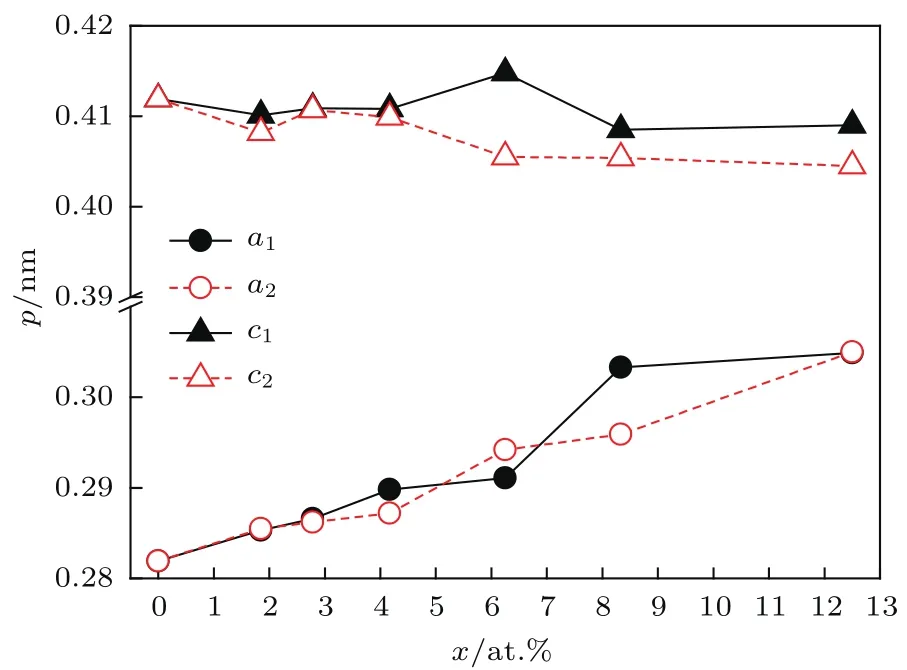
图3 (网刊彩色)La掺杂γ-T iA l体系的p-x曲线Fig.3. (color on line)The p-x cu rves of La-doped γ-T iA l system s.

在航空航天领域,低密度材料备受青睐.本文计算得到纯γ-TiA l体系的密度为3.8154 g·cm−3,与实验结果符合.尽管La掺杂使γ-TiA l合金体系的密度均有增加,但其密度仍在4.6 g·cm−3以下、远小于Ni基合金的密度(7.9–8.5 g·cm−3)[3],因而密度优势明显.

3.2 能量稳定性

晶体材料的可制备性和室温稳定性是材料研发的关键.原子平均形成能Ef是晶体体系能量稳定性的标志,较低的Ef预示体系具有较好的稳定性[27].对于La掺杂γ-TiA l体系,其原子平均形成能可表示为

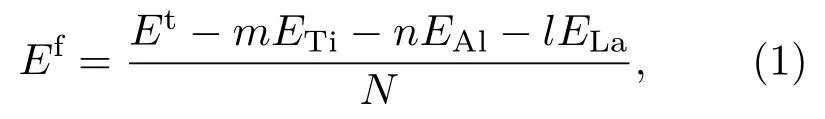
(1)式中,Et是几何优化后晶胞的总能量,各个体系的Et见表2;ETi,EAl和ELa为各个元素在单质情况下完全弛豫后的单原子能量,它们分别为−1603.0999,−56.3896和−862.4466 eV;m,n,l分别表示晶胞中Ti,A l和La的原子数;N为晶胞中的原子总数.根据(1)式计算得到各个体系的原子平均形成能,如表2所列.

由表2易知,各个La掺杂γ-TiA l体系的总能量和原子平均形成能均为负值,表明它们均具有较好的能量稳定性,即在一定实验条件下Ti1−xLax-A l,TiA l1−xLax(x = 1.85 at.%,2.78 at.%, 4.17 at.%,6.25 at.%,8.33 at.%,12.5 at.%)体系均可以实验制备并能稳定存在的.随着杂质浓度的增加,La掺杂γ-TiA l体系的原子平均形成能升高、能量稳定性降低.这意味着高浓度La掺杂γ-TiA l体系的制备条件较为苛刻.在同一杂质浓度x情况下,Ef(Ti1−xLaxA l)＜Ef′(TiA l1−xLax).这表明, Ti1−xLaxA l体系的能量稳定性高于TiA l1−xLax体系,即La原子替位掺杂时,它替代Ti原子的概率大于替代A l原子的概率.事实上,La倾向于替代Ti原子的现象可用置换固溶规律进行解释,Ti与La原子的共价半径(rLa=0.169 nm,rTi=0.136 nm)比较接近,掺杂引起的晶格畸变较小;相反,A l原子共价半径(rAl=0.118 nm)较小,La替代A l原子会引起较大的晶格畸变,使体系的晶格能量升高,稳定性降低.再者单质La和Ti晶体的空间群均为P 63/mm,而单质A l晶体的空间群为FMM,且La和Ti最外层电子数均为2,而A l原子最外层电子数为3.综合而言,La更倾向于替代Ti原子是微观物理机理所致.秦永和和乔英杰[23]曾预报La优先替代Ti8A l8体系中的A l原子.当然,在一定浓度情况下,La究竟优先取代哪一种元素仍需实验研究来确认;再者实验条件也是导致各种不同结果的影响因素.

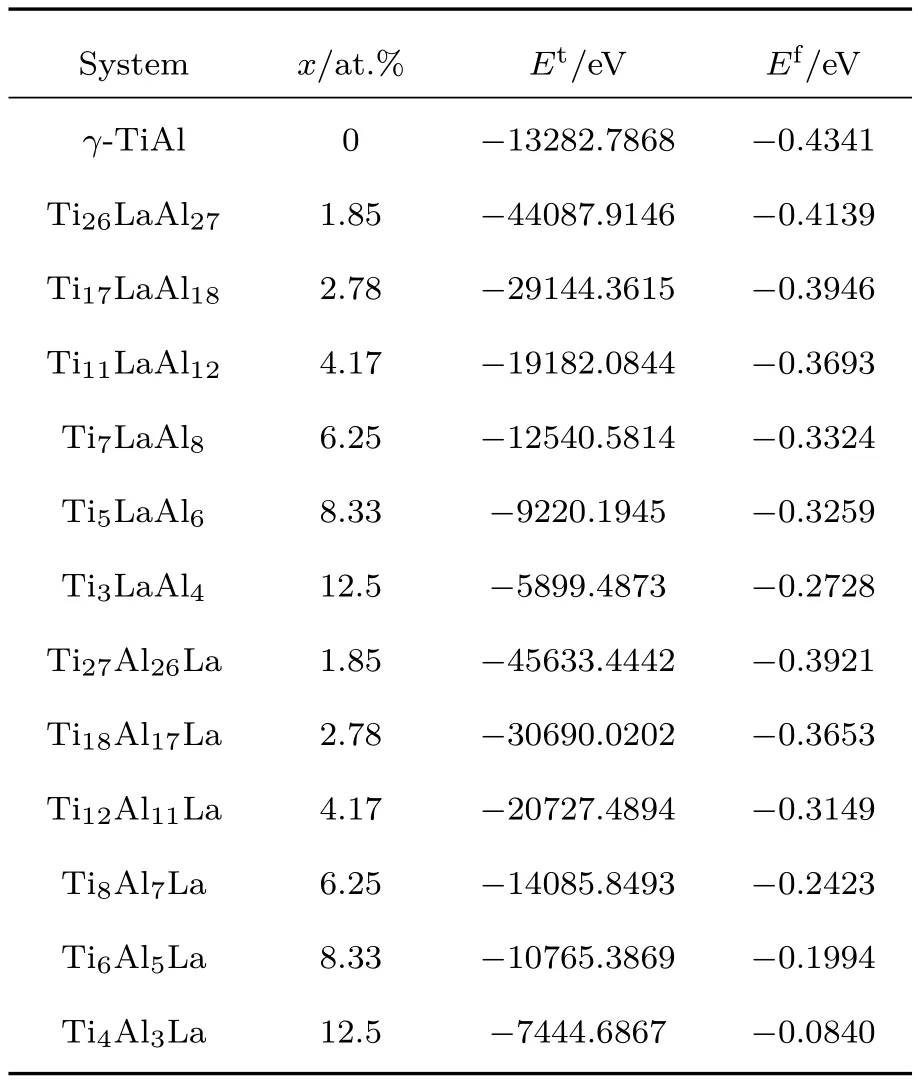
表2 La掺杂与纯γ-T iA l体系的能量性质Tab le 2.The energy p roperties of La-doped and pure γ-T iA l system s.

3.3 基于轴比和弹性模量的延性预报

Kawabata等[12]研究发现γ-TiA l基合金的延性可以用轴比R表征.R接近于1,晶体具有较高的对称性和变形协调性,滑移系数量多,合金材料的延性较好.根据表1中的轴比可绘制R-x曲线,如图4所示.其中R1对应Ti1−xLaxA l系列,R2对应TiA l1−xLax系列.

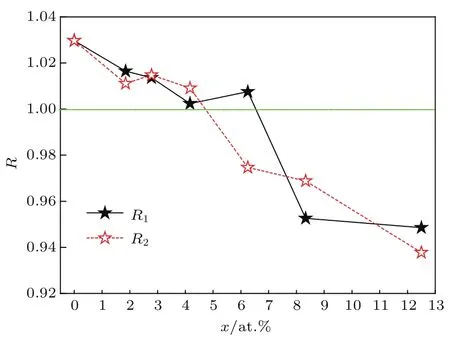
图4 (网刊彩色)La掺杂γ-T iA l体系的R-x曲线Fig.4.(color on line)The R-x curves of La-doped γ-T iA l system s.

图4显示,两条曲线中R均随x的增加呈下降趋势,并且在x位于4.0 at.%–7.0 at.%区间,曲线均与R=1直线相交.即对Ti1−xLaxA l和TiA l1−xLax系列,形式上分别存在一个浓度x01和x02使合金体系的R=1.此时体系的结构近似为立方结构.此结构的各向同性程度高,超位错和普通位错之间的差异小,即La掺杂体系的延性较纯γ-TiA l体系显著改善.

由图4容易看出,掺杂浓度x在1.85 at.%–7.0 at.%区域时,Ti1−xLaxA l体系的R均接近于1,预示有较好的延性. 同理,掺杂浓度x在1.85 at.%–5.25 at.%区域时,TiA l1−xLax体系的R也是接近于1,也预示有较好的延性.当掺杂浓度x超过 8.33 at.%时,合金体系的轴比明显偏离于1,不利于改善合金的延性.

必须提及的是,本文结果尚不能完全与陈仕奇等[19]的实验结果进行比较. 他们曾报道, 0.2 at.%–1.5 at.%的La可以提高TiA l合金的强度,而对延性仅在La含量为0.5 at.%以下时有改善作用,且在La浓度为0.2 at.%处,合金延性比TiA l高出一倍多.但他们的实验样品是多晶双相TiA l合金,除了主相γ-TiA l外,还有α2-Ti3A l相、相界、晶界以及其他杂质,包括非金属元素O等.但可以肯定,适量掺入La对于改善TiA l合金延性有积极作用.

综合以上计算分析可知,Ti11LaA l12体系的轴比最接近1、对改善延性最有利,并且其密度仅为3.993 g·cm−3.该密度值与目前工程所使用TiA l基合金的密度(3.7–3.9 g·cm−3)[3]相差不大.因此,以下主要研究Ti11LaA l12体系的性质,并与纯γ-TiA l体系进行对比分析.

通过计算得到Ti11LaA l12和Ti12A l12体系的弹性模量B,G与G/B的值如表3所列.研究表明,弹性模量比G/B=0.5,可作为材料延性的判据,G/B越小,材料的延性越好[28,29].Ti11LaA l12体系的G/B仅为0.485,远小于纯γ-TiA l体系的G/B(0.716).这表明Ti11LaA l12体系的延性明显优于纯γ-TiA l体系.这也从另一个维度预报了Ti11LaA l12体系具有较好的延性.

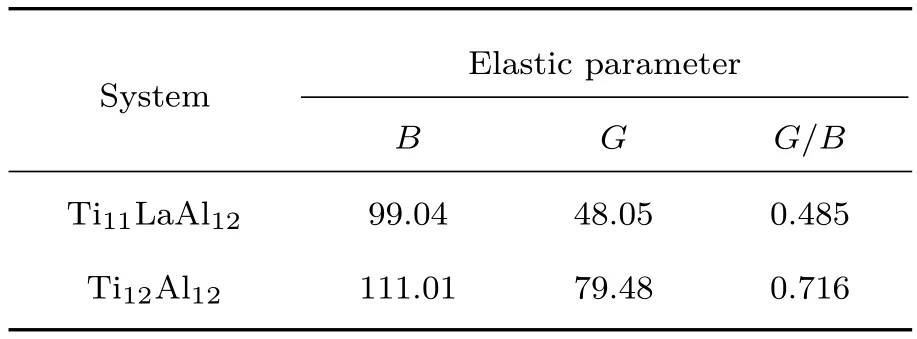
表3 Ti11LaA l12和T i12A l12体系的弹性参数Tab le 3. E lastic param eters of T i11LaA l12and T i12A l12system s.

3.4 T i11LaA l12和T i12A l12体系中的电荷分布和p-d轨道杂化

为了探索Ti11LaA l12体系延性改善的微观机理,计算出Ti11LaA l12和Ti12A l12体系中原子的M ulliken电荷布居数,如表4所列.

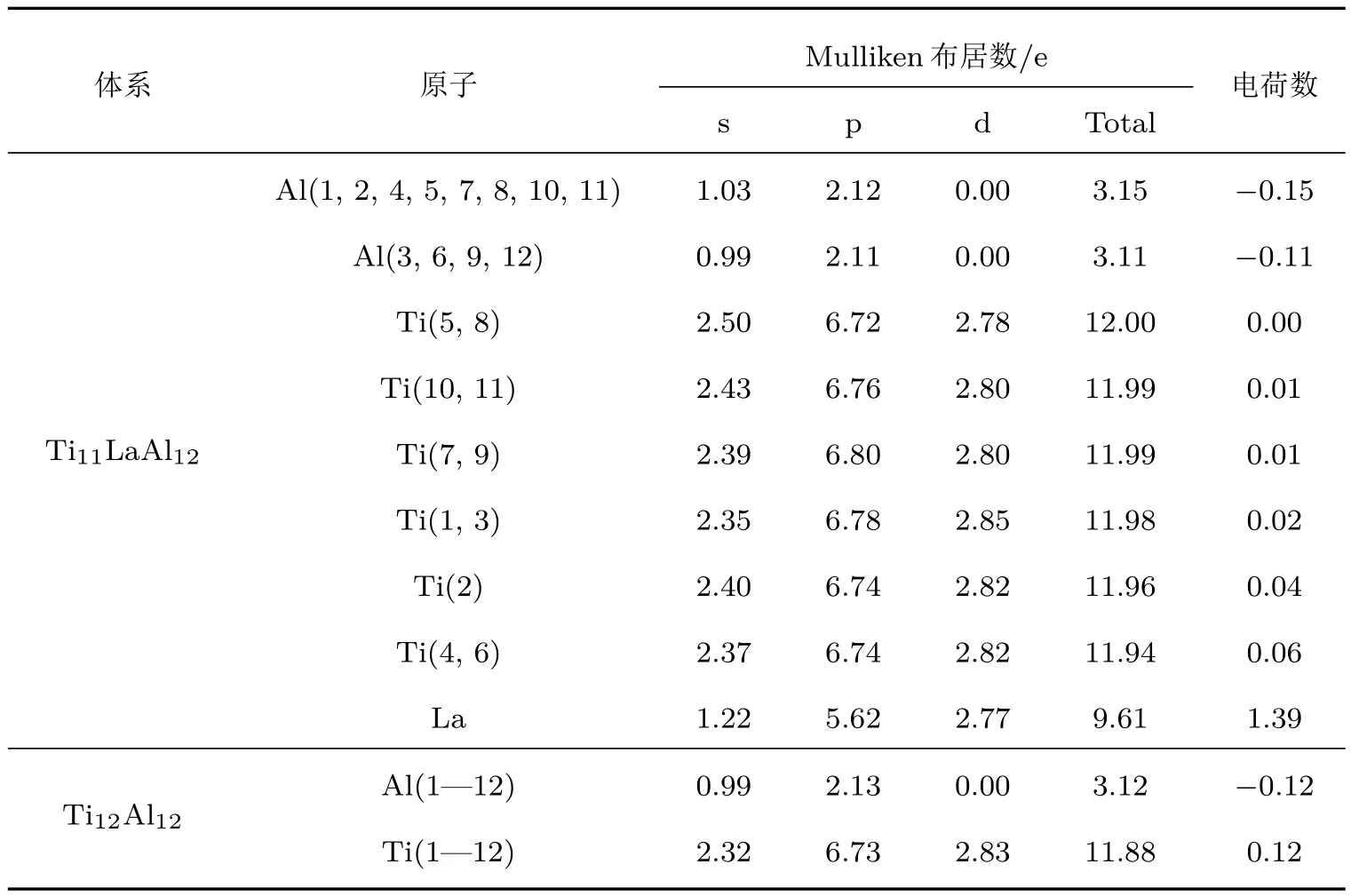
表4 T i11LaA l12和Ti12A l12体系中原子的M u lliken布居数Tab le 4.M u lliken popu lations of atom s in T i11LaA l12and T i12A l12system s.

对单原子,Ti原子中有2个未配对的3d电子; A l原子也有1个未配对的3p电子,它们均有很强的与其他电子配对的趋势.在Ti12A l12体系中,各个原子轨道上的电子分布与单原子有很大差异.总体上,A l原子夺得0.12 e,Ti原子失去0.12 e.A ls(A l原子的3s轨道)失去1.01 e,A l-p增加1.13 e; Ti-s(Ti原子的4s轨道)失去1.68 e,Ti-p(Ti原子的3p轨道)增加0.73 e,Ti-d增加0.83 e.原理上, Ti12A l12体系中存在几种化学键,原子键合情况比较复杂,本文仅以A l原子与其8个最近邻Ti原子的p-d轨道杂化为例进行分析.可以看出,A l周围能够参与p-d轨道杂化的远非1个A l-p电子和2个Ti-d电子,而是2.13个A l-p电子与2.83个Ti-d电子,即可能有4.96个电子参与轨道杂化.这决定了Ti与A l的p-d轨道杂化共价键强度较高;与此同时,每个A l周围可能有4.96个电子被p-d轨道杂化局域化.因此,在纯γ-TiA l合金中存在较强的、沿正六面体对角线方向的A l-p与Ti-d轨道杂化. Greenberg等[20]认为,方向性较强的p-d轨道杂化键是TiA l合金致脆的主要原因之一.总体上,参与轨道杂化形成共价键的电子数量增多,必然导致形成金属键的自由电子数量减少,金属键弱化.这个结果既可以定量解释黄宇阳等[30]的实验报道结果,也使党宏丽等[31]研究结果进一步定量化.

对Ti11LaA l12体系,La的加入引起各个原子轨道上的电子重新分布.为便于讨论,分别给Ti和A l原子编号,如图5所示.总体上,La原子失去1.39 e.A l原子可分为以下2类:1)与La处于最近邻的A l(1,2,4,5,7,8,10,11)总体各得到0.15 e, A l-s失去0.97 e,而A l-p得到1.12 e;2)非最近邻的A l(3,6,9,12)总体各得到0.11 e,A l-s失去1.01 e,而A l-p得到1.11 e.Ti原子得失电子情况比较复杂,可分为以下4类:1)Ti(5,8)总体无电子得失,Ti-s减少1.5 e,Ti-p和Ti-d分别增加0.72 e和0.78 e;2)Ti(7,9,10,11)总体失去0.01 e,同理, Ti-d增加0.8 e;3)Ti(1,3)总体失去电子0.02 e, Ti-d增加0.85 e;4)Ti(2)和Ti(4,6)总体分别失去0.04 e和0.06 e,Ti-d增加0.82 e.综合而言,La替代Ti原子后,它提供了较(Ti)多的电子,并诱导最近邻的A l原子得到电子的能力增强,同时所有Ti原子提供电子的能力减弱.

与Ti12A l12体系相比,Ti11LaA l12体系中除Ti(1,3)的3d轨道增加0.02 e外,其余Ti原子的3d轨道电子数均减少;La的5d轨道有2.77 e,较被取代的Ti-d减少0.06 e;每个A l-p的电子数均有减少.总体上可以判断,Ti11LaA l12体系中可提供参与p-d轨道杂化的电子数减少.

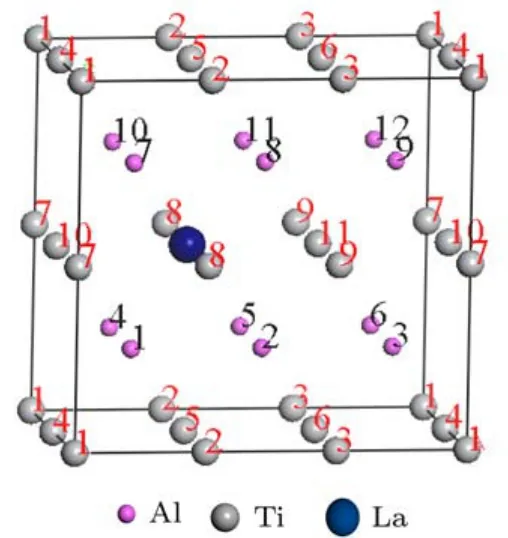
图5 (网刊彩色)T i11LaA l12体系中的原子位置Fig.5. (color on line)The positions of atom s in T i11LaA l12system s.

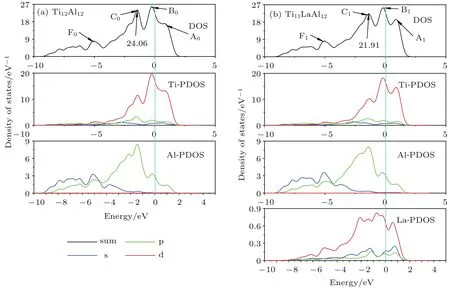
图6 (网刊彩色)T i12A l12和T i11LaA l12体系的DOSFig.6.(color on line)The DOS of T i12A l12and T i11LaA l12system s.

图6给出了Ti12A l12和Ti11LaA l12体系的电子DOS.由图6(a)可知,Ti12A l12体系的DOS出现四个成键峰,能级从高到低它们分别为A0(0.5–1.5 eV),B0(−1–0 eV),C0(−2–−1 eV)和F0(−5.5–−4.5 eV).通过该体系Ti和A l原子的分波态密度(PDOS)可知,A0和B0峰均主要有大量Ti-d电子和少量A l-p的电子贡献,即A0和B0峰主要为Ti–Ti键峰,同时还掺有少量的A l–Ti键峰.C0峰主要有Ti-d和A l-p电子贡献,即,C0峰为p-d轨道杂化峰;F0峰主要有A l原子的s和p贡献,即F0峰为A l–A l键峰.同理,Ti11LaA l12体系的DOS在相同的能级出现了成键峰A1,B1,C1和F1.与Ti12A l12体系的差别除了Ti和A l原子各轨道电子贡献的态密度不同,还有少量La-d(La原子的5d轨道)电子的贡献.

对比图6(b)与图6(a)可知,Ti11LaA l12体系的A l-p与Ti-d的分波态密度均低于Ti12A l12体系,导致Ti11LaA l12体系的p-d轨道杂化键峰(C1, 21.91 eV−1)低于Ti12A l12体系(C0,24.06 eV−1),即Ti11LaA l12体系的p-d轨道杂化键强度低于Ti12A l12体系.该结论与M ulliken电荷布居数所得结论一致,表明了本文分析的合理性.

3.5 杂质原子与其近邻原子间的相互作用对延性的影响

合金的性质与其内部化学键的性质密切相关.原子间的重叠布居数可以描述成键原子之间的相互作用性质[32]:重叠布居数为正,表示原子之间形成共价键相互作用,且数值越大共价键越强;重叠布居数为负,表示原子之间形成反键,两原子之间相互排斥.Ti11LaA l12体系延性显著改善和杂质原子与其近邻原子间的相互作用密不可分.表5给出了杂质La原子与其最近邻原子之间的重叠布居数.

由表5可知,La替代Ti原子掺杂后,Ti与La原子之间的重叠布居数为−2.37,即二者之间形成了反键.由表4可知,在Ti11LaA l12体系中,Ti与La原子均失去电子而成为正离子,即这两类原子靠近时会相互排斥.这也印证了两原子之间形成反键,故Ti与La原子之间没有共价特征.对比图6(a)和图6(b)可知,Ti11LaA l12体系的电子态密度在0.5–1.5 eV范围的成键峰A1很明显,且该峰的电子态密度由Ti-d电子与La-d电子贡献,而Ti12A l12体系在0.5–1.5 eV范围的成键峰A0并不明显.故Ti11LaA l12体系在该区域形成Ti-d–Lad成键峰.综上可知,La与其最近邻的Ti原子之间的相互作用和纯金属中原子间的相互作用类似.这对合金体系的金属性与延性有重要贡献.

表5 杂质La原子与其最近邻原子的重叠布居数Tab le 5.Overlap popu lations between La and itsnearest neighbor atom s.

同理,由表4可知,在Ti11LaA l12体系中,La原子失电子而形成正离子体,A l原子获得电子而形成负离子体,即两类原子靠近时会相互吸引而形成较强的离子键,故表5中没有二者之间的重叠布居数.根据Morrinaga理论[21],A l-p与Ti-d形成的共价键具有较强方向性,这是导致TiA l基合金脆性的根本原因.La替代Ti原子后,同一位置的原来方向性强的A l-p–Ti-d共价键,转化为无方向性的A l–La离子键.这意味着Ti11LaA l12体系的延性较纯γ-TiA l会明显改善.图7所示的Ti12A l12与Ti11LaA l12晶胞的(3 0 2)晶面的电荷密度图可以进一步佐证这一论点.

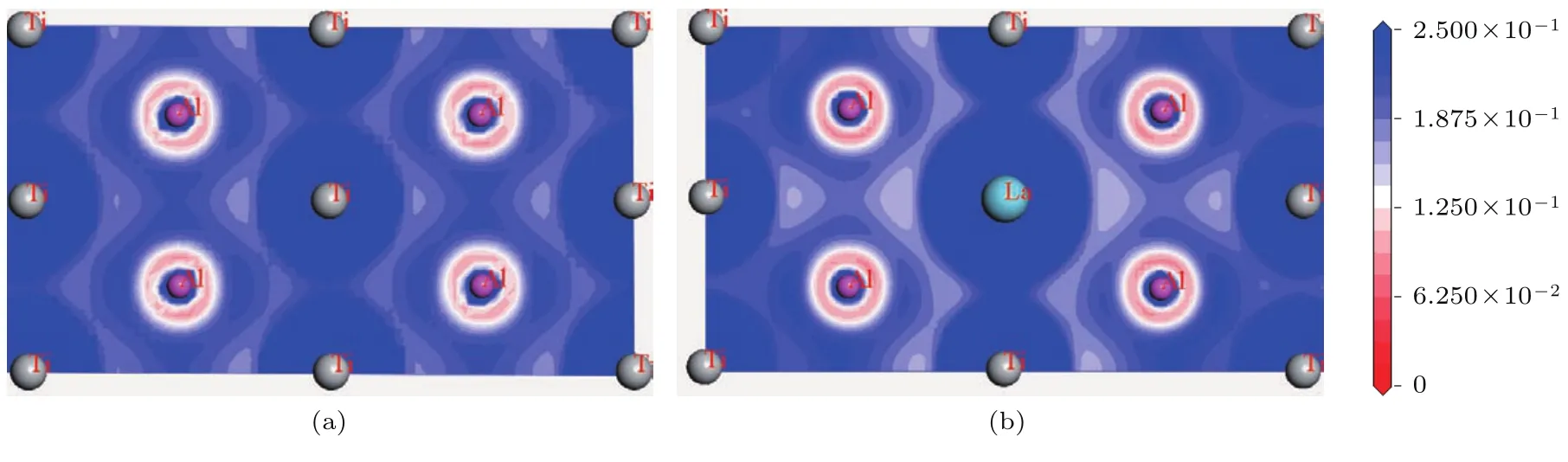
图7 (网刊彩色)(3 0 2)晶面的电荷密度图 (a)Ti12A l12;(b)Ti11LaA l12Fig.7.(color on line)The charge density m aps of(3 0 2)crystallographic p lane:(a)T i12A l12;(b)T i11LaA l12.

将图7(b)与图7(a)对比可知,Ti11LaA l12体系中Ti与La之间的电荷密度较大.而由表5可知, Ti与La之间没有共价结合特征,即Ti与La之间的电子不是被共价键局域化的,而是由正离子La和正离子Ti所共有,这正是金属键的特点.A l与La之间的电荷密度较小,表5也显示,A l与La之间没有共价特性,结合表4,La为正离子,A l为负离子,可推测,即A l与La之间形成离子键.

3.6 杂质引起合金中原有化学键的变化对延性的影响

虽然杂质La与其最近邻Ti,A l原子分别形成金属键、离子键.但合金中共价键Ti–Ti,A l–A l和A l–Ti仍占据主要成分.由于不同位置的A l和Ti原子的电荷分布差异较大,导致A l–A l,Ti–Ti和A l–Ti键的重叠布居数存在多种量值.为了便于分析,只取其平均值进行分析,详见表6.

对比掺杂前后共价键的重叠布居数可知,La替位Ti原子掺杂使合金体系中A l–A l共价键平均强度减弱;A l–Ti和Ti–Ti共价键平均强度增强.为了使该观点更有说服力,给出二者A l–A l成键晶面的差分电荷密度图(图8)和电荷密度图(图9).由图8可知,在A l层上,A l原子失去的电子多数分布在近邻的两个A l原子间的中部区域(蓝色).这也从另一方面说明在TiA l合金中,A l与A l原子之间形成较强的共价键.

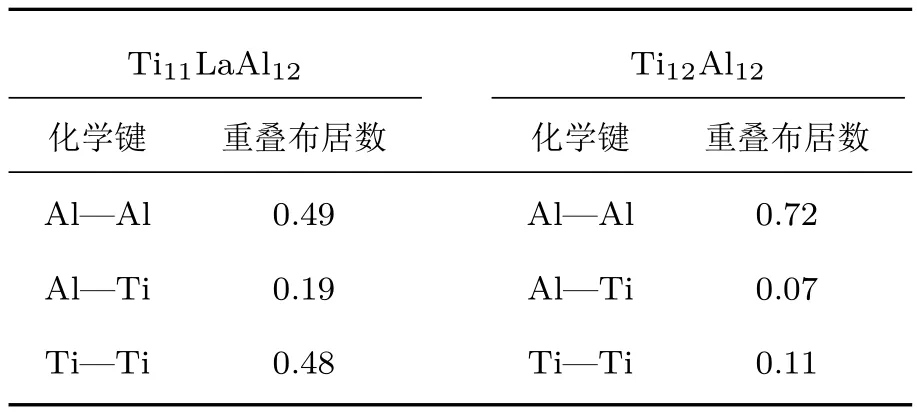
表6 T i11LaA l12和T i12A l12体系中的重叠布居数Tab le 6. Overlap popu lations of T i11LaA l12and T i12A l12system s.

为了便于描述,设D0Al-Al,D1Al-Al分别表示纯γ-TiA l与Ti11LaA l12合金体系中最近邻的A l与A l原子之间的电荷密度.对比图9(b)与图9(a)可以看出,D0Al-Al＞ D1Al-Al,即纯γ-TiA l合金体系中A l–A l共价结合强度大于Ti11LaA l12体系中A l–A l共价结合强度.也就是说,La原子掺杂后使体系中A l–A l共价键强度减弱.该结论与重叠布居数显示结论一致.

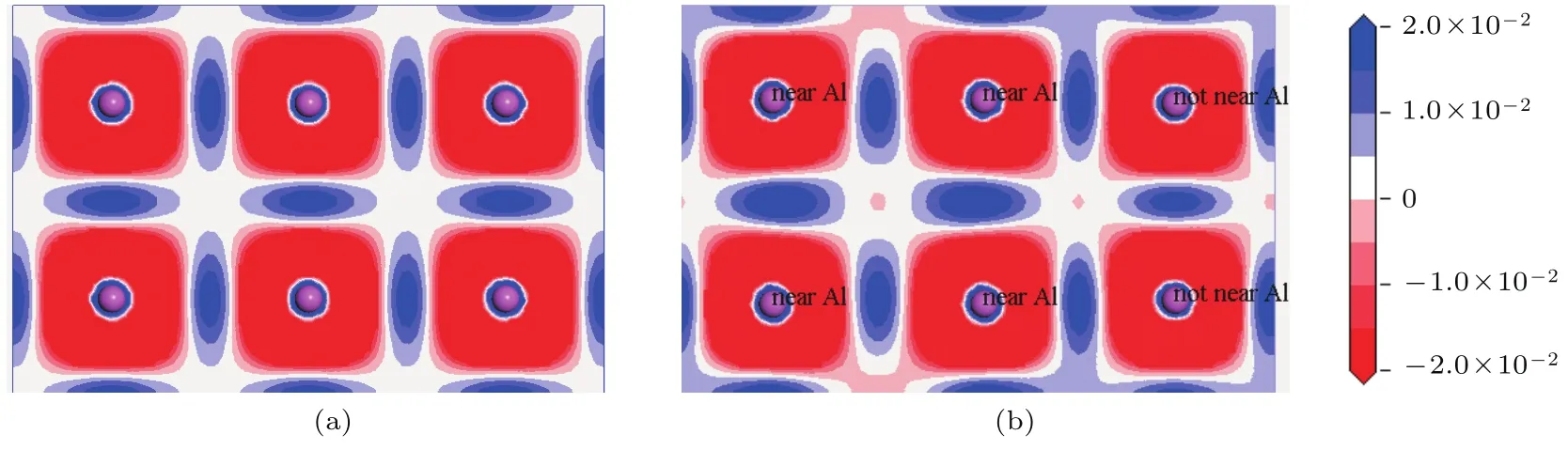
图8 (网刊彩色)差分电荷密度图 (a)T i12A l12体系;(b)T i11LaA l12体系Fig.8.(color on line)Them aps of the charge density diff erence:(a)T i12A l12system;(b)T i11LaA l12system.

图9 (网刊彩色)电荷密度图 (a)T i12A l12体系;(b)T i11LaA l12体系Fig.9.(color on line)Them aps of the charge density:(a)T i12A l12system;(b)T i11LaA l12system.

另外,根据3.5节所述,体系中A l-p–Ti-d轨道杂化键强度大小关系为:A l-p–Ti-d(Ti11LaA l12)＜ A l-p–Ti-d(Ti12A l12). 但重叠布居数显示A l–Ti(Ti11LaA l12)＞A l–Ti(Ti11LaA l12).由此看见TiA l合金体系中A l与Ti原子之间的共价键种类不止A l-p–Ti-d一种,可能存在A l-s(或p)–Ti-s(或p或d)共价键.

上述合金体系中共价键的变化会导致A l–A l, A l–Ti,Ti–Ti三种化学键的强度差异程度发生变化.总体上Ti11LaA l12体系中三种共价键强度差异明显低于Ti12A l12体系.这表明La掺杂使合金体系中化学键A l–A l,A l–Ti,Ti–Ti的强度明显趋同,各向同性程度明显高于纯γ-TiA l体系的各向同性程度.因为体系的各向同性程度越高,延性越好[20].因此预报Ti11LaA l12体系的延性高于纯γ-TiA l体系.

4 结 论

综合以上对纯γ-TiA l,TiA l1−xLax及Ti1−x-LaxA l(x=1.85 at.%,2.78 at.%,4.17 at.%, 6.25 at.%,8.33 at.%,12.5 at.%)合金体系的稳定性及其晶体结构和延性的计算与理论分析,可知: 1)杂质La的浓度x≤12.5 at.%,各个体系均具有较好的能量稳定性,即在一定条件下它们是可以实验制备的;随着La浓度的增加合金体系的能量稳定性降低;2)La的低浓度(x≤6.25 at.%)掺杂使合金体系的轴比较纯γ-TiA l更接近于1,这对于改善材料的延性极为有利,其中Ti11LaA l12体系的轴比最接近于1,预报其延性最佳;La浓度超过8.33 at.%,合金的轴比明显偏离于1,这不利于改善材料的延性.

通过对Ti11LaA l12和Ti12A l12体系的布居数、电荷密度和电子态密度的计算分析与比较,发现La替代Ti原子导致Ti11LaA l12体系的电子性质较Ti12A l12体系发生以下变化:1)合金体系内Ti-d轨道和A l-p轨道的电子数均减小,可被p-d杂化轨道局域化的电子数减小、p-d轨道杂化键强度降低,位错运动的阻力减少,从而Ti11LaA l12体系的延性得以明显改善;2)La与其最近邻A l原子之间均形成离子键,而与其最近邻Ti原子之间均形成金属键,这些化学键的共价性较原来的A l–Ti和Ti–Ti键减弱,导致合金的金属性增强,从而使该类合金的延性得以改善;3)掺杂体系中A l–A l键的平均强度减弱,A l–Ti键和Ti–Ti键的平均强度增强,三者的强度差异明显减小,晶体结构的各向异性程度降低,从而使该类合金材料的延性得以改善.

[1]Castillo-Rod riguez M,No M L,Jim enez J A,Ruano O A,Juan J S 2016 Acta M ater.103 46

[2]Bew lay B P,Nag S,Suzuki A,W eim er M J 2016 Mater. H igh Tem p.33 549

[3]Q ian J H,Q i X Z 2002 Chin.J.Rare M etal.26 477(in Chinese)[钱九红,祁学忠2002稀有金属26 477]

[4]Pollock T M 2016 Nat.M ater.15 809

[5]K awab ta T,Tam u ra T,Izum i O 1993 M etall.Trans.A 24 141

[6]Song Q G,Q in G S,Yang B B,Jiang Q J,Hu X L 2016 Acta Phys.Sin.65 046102(in Chinese)[宋庆功,秦国顺,杨宝宝,蒋清杰,胡雪兰2016物理学报65 046102]

[7]Yam aguchi M,Ito K 2000 Acta M ater.48 307

[8]K awabata T,Izum i O 1987 Philos.M ag.A 55 823

[9]Huang SC,Hall E L 1991 Acta M etall.M ater.39 1053

[10]Pu Z J,Shi J D,Zou D S,Zhong Z Y 1993 Acta M etall. Sin.29 31(in Chinese)[蒲忠杰,石建东,邹敦叙,仲增墉1993金属学报29 31]

[11]Chen G,Peng Y B,Zheng G,Q i Z X,W ang M Z,Yu H C,Dong C L,Liu C T 2016 Nat.M ater.15 876

[12]K awabata T,Takezono Y,Kanai T,O Izum i 1988 Acta M etall.M ater.36 963

[13]Song X P,Chen G L 2002 Acta M eta ll.Sin.38 583(in Chinese)[宋西平,陈国良2002金属学报38 583]

[14]Yang R 2015 Acta M etall.Sin.51 129(in Chinese)[杨锐2015金属学报51 129]

[15]Hu H,W u X Z,W ang R,LiW G,Liu Q 2016 J.A lloys Com pd.658 689

[16]Yang Z J,Sun H L,Huang Z W,Zhu D G,W ang L H 2015 M ater.Rev.:Rev.29 85(in Chinese)[杨镇骏,孙红亮,黄泽文,朱德贵,王良辉2015材料导报:综述篇29 85]

[17]Xu F S,Geng H R,W ang S R 2009 Rare M etal.M at. Eng.38 361(in Chinese)[徐福松,耿浩然,王守仁2009稀有金属材料与工程38 361]

[18]Had i M,M eratian M,Shafyei A 2015 J.A lloys Com pd. 618 27

[19]Chen S Q,Qu X H,Lei C M,Huang B Y 1994 Acta M etall.Sin.30 20(in Chinese)[陈仕奇,曲选辉,雷长明,黄伯云1994金属学报30 20]

[20]G reenberg B A,Antonov O V,Indenbaum V N,Karkin L E,Notkin A B,Ponom arev M V,Sm irnov L V 1991 Acta M eta ll.M ater.39 233

[21]M orinaga M,Saito J,Yukawa N,Adachi H 1990 Acta M etall.M ater.38 25

[22]Eberhart M E,Clougherty D P,M aclaren JM 1993 Philos.M ag.B 68 455

[23]Q in Y H,Qiao Y J 2015 J.Harbin Inst.Technol.47 123 (in Chinese)[秦永和,乔英杰 2015哈尔滨工业大学学报47 123]

[24]Pau l R,K atherine C E,Philip D F A,Casey F,M alia B W,Aurelio M,M atthias Z,Sorelle A F,Joshua S, A lexander J N 2016 Nature 533 73

[25]Song Q G 2004 Chin.Sci.Bu ll.49 210

[26]Chen G L,Lin J P 1999 Physicalm eta llurgy Basis ofOrdered In term etallic Com pound Structure M ateria ls(Beijing:M etallu rgical Industry Press)p285(in Chinese)[陈国良,林均品1999有序金属间化合物结构材料物理金属学基础(北京:冶金工业出版社)第285页]

[27]Shang J X,Yu T B 2009 Acta Phys.Sin.58 1179(in Chinese)[尚家香,于潭波2009物理学报58 1179]

[28]Pugh S F 1954 Philos.M ag.45 823

[29]Fu C L 1990 J.M ater.Res.5 971

[30]Huang Y Y,W u W M,Deng W,Zhong X P,X iong L Y,Cao M Z,Long Q W 2000 Chin.J.Nonferr.M et.10 796(in Chinese)[黄宇阳,吴伟明,邓文,钟夏平,熊良钺,曹名洲,龙期威2000中国有色金属学报10 796]

[31]Dang H L,W ang C Y,Yu T 2007 Acta Phys.Sin.56 2838(in Chinese)[党宏丽,王崇愚,于涛 2007物理学报56 2838]

[32]Liu X K,Liu Y,Zheng Z,Dai J L 2010 Rare M etal. M at.Eng.39 832(in Chinese)[刘显坤,刘颖,郑州,代君龙2010稀有金属材料与工程39 832]

PACS:61.66.Dk,61.50.Ah,62.20.fk,68.65.–kDOI:10.7498/aps.66.066103

Ductile and electron ic p roperties o f La-doped gamm a-T iA l system s based on density functional theory∗

Song Qing-Gong1)2)†Zhao Jun-Pu1)Gu Wei-Feng1)Zhen Dan-Dan2)Guo Yan-Rui1)Li Ze-Peng1)

1)(Institu te of Low D im ensional M aterials and Technology,College of Science,Civil Aviation University of China, T ianjin 300300,China)
2)(Sino-European Institute of Aviation Engineering,Civil Aviation University ofChina,Tianjin 300300,China)
(Received 9 Novem ber 2016;revised m anuscrip t received 10 Decem ber 2016)

Because of the low density,high specific strength and excellent perform ance at high tem perature,γ-TiA l based alloy has becom e a new generation ofm aterials in the aeronautic field.However,its poor ductility at room tem perature set a lim itation to its w ide app lications.In this paper,the crystal structures,stabilities and ductilities of La-doped γ-TiA l system s are investigated by using fi rst princip lesm ethod based on density functional theory,in which T ior A l is substituted by La and the im purity content valuesare 1.85 at.%,2.78 at.%,4.17 at.%,6.25 at.%,8.33 at.%and 12.5 at.%, respectively.The resu lts show that all of the La-doped alloys have good energy stabilities,nam ely they can be p repared experimentally,when the im purity concentration x of system is less than or equal to 12.5 at.%.And the density of the La-doped system is less than 4.6 g·cm−3.La doping induces the lattice parameters and the axial ratio of the alloy system to change.The axial ratio of La-doped system w ith low im purity concentration(x≤6.25 at.%)is closer to 1,which is very beneficial to im proving the ductility of the m aterials.It is predicted that the system T i11LaA l12would have the best ductility among those of the investigated system s,for its axial ratio is the closest to 1.The electronic eff ect about the ductility of La-doped system is discussed through the com parisons of the popu lations,charge densities and densities between the states of system s T i11LaA l12and Ti12A l12.It is found that the system Ti11LaA l12presents a state of electron redistribution in valence electron orbitals of A l and Ti due to an atom of titanium substituted w ith that of lanthanum.The charge numbers of T i-d and A l-p orbitals and the numbers of electrons can be delocalized by reducing the p-d orbital hybridization.Thus,the intensity of p-d orbital hybridization is weakened,the resistance of dislocation m ovem ent is reduced,and the ductility of T iA l system s can be im proved.Actually,the new electron redistribution shows diff erent properties of som e chem ical bonds,in which som e of covalent A l—T ibonds are rep laced by ionic A l—La bonds and some of covalent Ti—Tibonds are rep laced bymetallic Ti—La bonds.Therefore,the covalent and directional properties of chem ical bonds are reduced distinctly while the m etallic properties of m aterials are strengthened.The average intensity of A l—A l bonds decreases and those of A l—Tiand Ti—T ibonds are increased in the La-dopedγ-T iA l system(Ti11LaA l12).As a result,the diff erences between the three kinds of chem ical bonds dim inish and the degree of isotropy of the crystal structure increases,which can greatly im prove the ductility ofγ-T iA l alloy.

La-dopedγ-TiA l,crystal structure,ductility,electronic property

10.7498/aps.66.066103

∗国家自然科学基金(批准号:11304380)和中央高校基本科研业务费专项资金(批准号:3122014K 001)资助的课题.

†通信作者.E-m ail:qgsong@cauc.edu.cn

*Project supported by the National Natural Science Foundation of China(G rant No.11304380)and the Fundam ental Research Funds for the Central Universities,China(G rant No.3122014K 001).

†Corresponding author.E-m ail:qgsong@cauc.edu.cn