ZnH分子激发态的电子结构和跃迁性质的理论计算∗
2017-08-03赵书涛梁桂颖李瑞李奇楠张志国闫冰
赵书涛梁桂颖 李瑞 李奇楠 张志国 闫冰‡
1)(阜阳师范学院物理与电子工程学院,阜阳 236037)
2)(吉林省应用原子与分子光谱重点实验室(吉林大学),吉林大学原子与分子物理研究所,长春 130012)
3)(齐齐哈尔大学理学院物理系,齐齐哈尔 161006)
(2016年12月7日收到;2017年1月23日收到修改稿)
ZnH分子激发态的电子结构和跃迁性质的理论计算∗
赵书涛1)2)†梁桂颖2)李瑞3)李奇楠3)张志国1)闫冰2)‡
1)(阜阳师范学院物理与电子工程学院,阜阳 236037)
2)(吉林省应用原子与分子光谱重点实验室(吉林大学),吉林大学原子与分子物理研究所,长春 130012)
3)(齐齐哈尔大学理学院物理系,齐齐哈尔 161006)
(2016年12月7日收到;2017年1月23日收到修改稿)
采用高精度的多参考组态相互作用方法计算了ZnH分子的能量最低四个离解限Zn(1Sg)+H(2Sg), Zn(3Pu)+H(2Sg),Zn+(2Sg)+H−(1Sg)和Zn(1Pu)+H(2Sg)对应的7个Λ-S态的势能曲线.计算中考虑了Davidson修正、标量相对论效应、自旋-轨道耦合效应和芯-价电子关联.基于计算的Λ-S和Ω态的势能曲线,数值求解一维径向Schrödinger方程得到了束缚电子态的光谱常数,理论计算结果与之前的实验结果符合较好.计算得到了7个Λ-S态的电偶极矩随核间距的变化曲线,分析了电子组态成分变化对电偶极矩和成键性质的影响.计算结果表明,C2Σ+态是一个离子对态.进一步地,分析了避免交叉点附近Ω态的Λ-S态组成的变化规律,讨论了避免交叉现象对跃迁偶极矩的影响.基于计算的跃迁偶极矩、Franck-Condon因子和振动能级信息,给出了束缚激发态(2)1/2,(3)1/2,(4)1/2和(1)3/2的v′=0—2振动能级的自发发射寿命,结果与现有实验值相符合.
ZnH,多参考组态相互作用方法,光谱常数,辐射寿命
1 引 言
Zn元素是化学、生物和材料中的一种重要组成元素,它的氢化物在天体物理、电池降解、复杂催化、化学成键和吸附及金属储氢中扮演着重要的角色,引起了研究者们的极大关注[1−3].另外,ZnH作为最简单的含IIB族金属Zn的中性双原子分子,其价电子非常少,对其进行精确的光谱测量和高精度的电子结构从头计算研究,已成为光谱学和分子物理领域中的一个研究热点[4,5].
早在1930年,Watson[6]对ZnH分子的A2Π→ X2Σ+的塞曼效应进行了实验研究;1937年, Fujioka和Tanaka对ZnH分子的A2Π→X2Σ+和B2Σ+→X2Σ+跃迁进行了观测和分析,并给出了这些电子态的光谱常数[7].1940年,M rozowski[8]通过法布里-珀罗标准具在430 nm附近对ZnH分子的A2Π1/2→X2Σ+的(0,0)谱带进行了测量,并分析了同位素位移对谱线的影响.1962年,Khan[9]在242.646 nm处发现了ZnH分子的新谱带,将其指认为C2Σ+←X2Σ+跃迁,给出了基态X2Σ+和C2Σ+的光谱常数,并发现吸收光谱的转动光谱是弥散的,推断上激发态C2Σ+发生了预解离,并预测这个预解离是由四重态4Σ+或4Π导致.1990年,Urban等[10]对ZnH的四种同位素分子的基态红外光谱进行了测量,并给出了基态电子态的Dunham参数.2006年,Shayesteh等[11]利用傅立叶变换光谱仪对基态X2Σ+的ν=1→0和ν=2→ 1的谱带进行了高分辨的红外发射光谱探测,给出了基态的平衡核间距Re=1.593478Å,转动常数Be=6.69133 cm−1.2013年,Bucchino和Ziurys[5]对67ZnH同位素分子的X2Σ+态的超精细结构进行了太赫兹光谱探测,指出它的成键具有共价键特征.
1967年,Ishiguro和Kobori[12]对ZnH分子的激发态A2Π首次进行了自旋-轨道耦合效应的考虑,其中忽略了双中心积分,只通过原子的自旋-轨道耦合常数给出了分子激发态的旋-轨耦合常数.1971年,Veseth[13]将A2Π态的旋-轨耦合常数表示成与分子核间距相关的更复杂、精确的表达式.1986年,Chong等[14,15]采用单双组态相互作用(SDCI)、耦合对泛函(CPF)和修正耦合对泛函(MCPF)方法对ZnH分子的基态X2Σ+进行了精确的全电子计算,并得到了光谱常数和偶极矩,但并未涉及激发态的精细结构计算.1993年, Jamorski等[16]利用相对论有效势和芯极化势,采用组态相互作用(CI)方法研究了ZnH分子的基态和低激发态的电子结构,并给出了部分电子态的光谱常数.2006年,Kerkines等[17]采用高精度的耦合簇理论(RCCSD(T))计算了基态X2Σ+的平衡位置、解离能和偶极矩.2009年,Hayashi等[4]采用多参考组态相互作用(MRCI)方法计算了与ZnH最低两个离解限相关联的5个Λ-S态的势能曲线,并给出了相应的光谱常数,对更高离解限的Λ-S态及自旋-轨道耦合的Ω态势能曲线未做研究. 2010年,王玲等[18]采用密度泛函B3LYP方法计算了ZnH及其离子的基态的势能函数,得到了光谱常数.综上,早期的理论研究主要采用了有效势代替芯壳层电子,只对少数的价电子进行了组态相互作用计算;芯-价电子关联作用通过极化势进行计算.而近期的理论计算主要集中在基态X2Σ+和第一激发态A2Π态的光谱常数、电偶极矩和解离能,对较高激发态未做过多探讨.近年来,相关的研究工作[19−21]表明电子态之间的自旋-轨道耦合效应对激发态电子结构和光谱有明显的影响.因此,本文考虑标量相对论效应、芯-价电子关联和自旋-轨道耦合效应对较高激发态进行系统的研究.
本文采用MRCI方法,考虑标量相对论效应和芯-价壳层电子关联效应后,对ZnH分子的四个离解限Zn(1Sg)+H(2Sg),Zn(3Pu)+H(2Sg), Zn+(2Sg)+H−(1Sg)和Zn(1Pu)+H(2Sg)对应的7个Λ-S态的势能曲线进行了从头计算研究.基于获得的Λ-S态的势能曲线,给出了所有束缚态的光谱常数.考虑自旋-轨道耦合效应后计算了Ω态的势能曲线,并给出了较低的束缚Ω态的光谱常数.最后,给出了Ω=1/2和Ω=3/2态到基态的跃迁偶极矩曲线,计算了(2)1/2,(3)1/2,(4)1/2和(1)3/2到基态X1/2跃迁的Frank-Condon因子,结合跃迁偶极矩、激发能和激发态与基态间的Frank-Condon因子给出了(2)1/2,(3)1/2,(4)1/2和(1)3/2的v′=0—2的能级辐射寿命.
2 计算方法
采用Werner等[22]开发的量化程序包MOLPRO2010,对ZnH分子进行从头计算.由于程序自身的限制,ZnH分子的C∞ν群的对称性在实际计算过程中用C2ν群代替,两者之间的不可约表示对应关系为Σ+=A1,Π=B1+B2,Δ=A1+A2, Σ−=A2.为了兼顾效率和精度,我们为Zn和H原子选取完全收缩aug-cc-pwCVTZ-DK基组[23],在核间距R=0.8—6.0Å上对ZnH分子进行了单点能计算.在计算时,首先采用Hartree-Fock (HF)方法对ZnH分子的基态(X2Σ+)波函数进行计算,然后以此波函数为基础,采用完全活性空间自洽场(CASSCF)方法进行优化[24,25],最后,以优化的波函数为参考,对分子的Λ-S态进行包含Davidson(+Q)修正的MRCI计算[26,27].在CASSCF计算时,双占据轨道由1s2s2p3s3p3d(Zn)构成,活性空间为4s4p5s(Zn)和1s(H)构成的6个分子轨道4a1,1b1和1b2.在MRCI+Q计算时,将Zn的1s2s2p壳层的电子放入冻芯轨道,活性空间的分子轨道则由4s4p5s(Zn)和1s(H)构成,并将Zn的3s23p63d10电子作为关联电子.因此,在此计算过程中考虑了ZnH分子的21个电子的关联效应.进一步,通过Breit-Pauli算符将自旋-轨道耦合作为微扰,对角化自旋-轨道哈密顿矩阵[28−30],获得了自旋-轨道耦合矩阵的本征能量和本征函数,并最终给出了Ω态的势能曲线.
基于计算的ZnH自由基的Λ-S态和Ω态势能曲线,采用LEVEL8.0程序[31]求解核径向的一维Schrödinger方程,给出束缚态的光谱常数,并对(2)1/2,(3)1/2,(4)1/2和(1)3/2的v′=0—2振动能级的辐射寿命进行了预测.
3 结果与讨论
3.1 Λ-S态的势能曲线、光谱常数和偶极矩
在MRCI+Q/aug-cc-pwCVTZ-DK理论水平上计算了ZnH分子四个离解限Zn(1Sg)+H(2Sg), Zn(3Pu)+ H(2Sg), Zn+(2Sg)+ H−(1Sg)和Zn(1Pu)+H(2Sg)对应的7个Λ-S态的势能曲线,如图1所示.可见,X2Σ+,A2Π,B2Σ+,C2Σ+和22Π为束缚态,14Σ+和14Π为排斥态.这些束缚态的光谱常数包括绝热激发能Te,振动常数ωe和 ωeχe,平衡转动常数Be和平衡核间距Re,以及Re附近的主要电子组态列于表1.
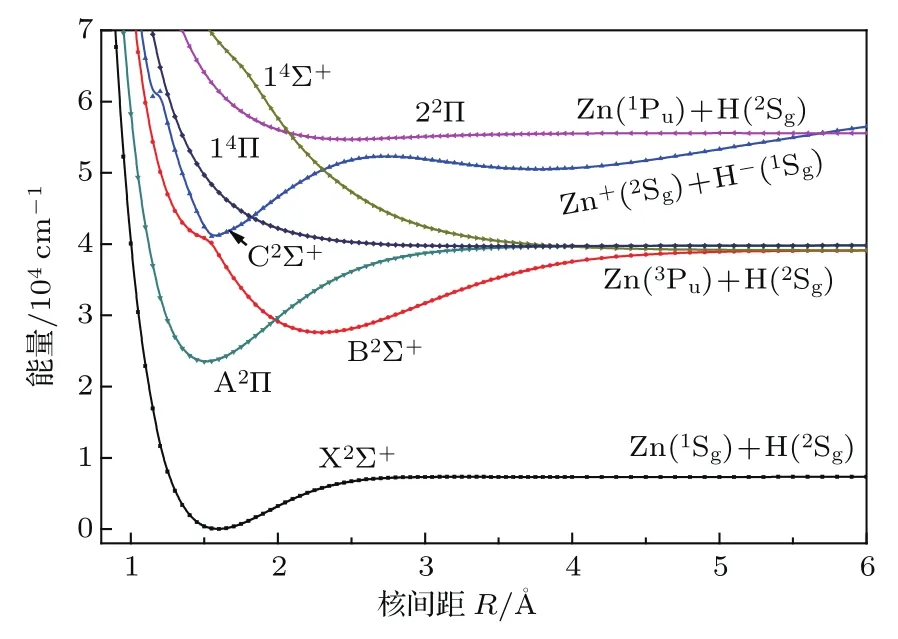
图1 (网刊彩色)ZnH分子的Λ-S态势能曲线Fig.1.(color on line)Potential energy curves of the Λ-S states of ZnH.

表1 ZnH分子Λ-S态的光谱常数Tab le 1.Spectroscop ic constants of theΛ-S states of ZnH.
基态X2Σ+的平衡核间距Re为1.5926Å,平衡位置的主要电子组态为7σ28σα,其中7σ和8σ分子轨道主要由Zn的4s与H的1s原子轨道线性组合而成,具有明显的共价键性质,与之前的实验预测相一致[5];9σ,10σ分子轨道分别主要对应于Zn的5s,4pz原子轨道.该电子态的光谱常数与先前的实验值相符合[3];Be和Re与最新的实验值差值[11]仅为0.0113 cm−1和0.0009Å.基态的离解能De为0.91 eV,与实验值(0.95±0.02)eV[16]和最新的高精度理论值0.92 eV[17]接近.第二解离限对应4个电子态A2Π,B2Σ+,14Π和14Σ+,在我们计算的最大核间距6Å处,这些电子态在几十到几百cm−1误差范围内简并.此种在较大原子间距处不严格的简并可能是由于描述不同多重度的电子态所用的组态函数数目不同所致,这也是采用固定活性空间的截断的组态相互作用方法的一个不足.在平衡核间距附近,第一激发态A2Π的主要组态为7σ24πα,主要对应于Zn的4sσ→4pπ的单电子跃迁,与基态类似,该电子态也显示出较强的共价键特征.A2Π态的光谱常数Te,ωe,ωexe和Re分别为2.91 eV,1903 cm−1,40.57 cm−1和1.514Å,与实验值[3]2.90 eV,1910 cm−1,40.8 cm−1和1.512Å和最新的理论值[4]2.89 eV,1907 cm−1,40 cm−1, 1.509Å均符合得很好.与基态相比,A2Π态存在较深的势阱,本文理论计算的离解能为2.02 eV,与最近的理论值[4]2.04 eV接近,与实验值[3]的偏差为0.08 eV.A2Π态与第二激发态B2Σ+在核间距R= 2.0Å附近相交,这与之前的理论预测[4]1.98Å符合,考虑自旋-轨道耦合作用后,Ω=1/2成分会形成避免交叉,这将在后面详细讨论.B2Σ+态的主要电子组态为7σα8σ2,对应7σ→8σ的单电子跃迁,它的离解能比A2Π的小0.6 eV,为1.42 eV,与最新的理论值[4]1.44 eV十分接近,比实验值[3]1.52 eV低了0.1 eV.在R=1.55Å附近,B2Σ+与C2Σ+形成避免交叉,在此区域离子键与共价键共存,并将导致它们电子组态的变化.如图2所示:在R<1.55Å处,B2Σ+和C2Σ+的主要组态分别为7σ29σα和7σα8σ2;在R=1.55Å附近,这两个电子态的组态成分急剧变化并互换,主要组态变为7σα8σ2和7σ29σα.C2Σ+是具有双势阱的电子态,绝热地关联于离子对解离限Zn+(2Sg)+H−(1Sg),这可以从后面的偶极矩讨论部分得证;它的主要组态为7σ29σα和7σα8σ2,对应于8σ→ 9σ和7σ→8σ的单电子跃迁的组合,C2Σ+态Te的理论计算值为5.08 eV,与实验值[3]的差值仅为0.01 eV, ωe和ωexe与实验值[3]有较大的偏差,这可能由于它与B2Σ+在R=1.55Å处的非绝热耦合引起的. C2Σ+态右侧势阱的光谱参数尚无理论和实验报道,本文结果可为后续研究提供参考.在R=1.85和2.30Å附近,它和排斥态14Π和14Σ+分别交叉,考虑自旋-轨道相互作用后,在交叉点附近的这些Λ-S态耦合后的Ω态会发生避免交叉现象,这将在以下两小节详细讨论.22Π态的光谱常数和离解能De尚无实验和理论值报道,本文的计算结果可以为后续的研究提供参考.
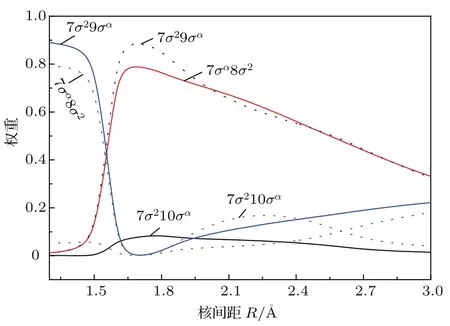
图2 (网刊彩色)B2Σ+(实线)和C2Σ+(点线)组态成分随分子间距离的变化Fig.2.(color on line)The R-dependent weights of the dom inated electronic con figu rations of B2Σ+(solid lines)and C2Σ+(dot lines).
由于偶极矩反映了分子的成键性质,本文对ZnH分子的7个Λ-S态的电偶极矩进行了理论计算,它们随分子核间距R变化的曲线如图3所示.从图3可以看出:在核间距较大(如R=6.0Å)时, C2Σ+的偶极矩很大(20 Debye),表明分子具有离子特性,正如上文所述,其对应的离解限为离子对;其他电子态的偶极矩趋向于零,表明对应的离解极限为中性原子.实验表明,与ZnF分子的离子键情况不同,ZnH分子基态X2Σ+在平衡位置时具有共价键特点[5].本文X2Σ+的偶极矩在平衡位置时的大小为0.06 Debye,与理论值[4]0.04接近,表明该电子态具有共价键特点.在核间距R=1.55Å附近,如上文和图1所示,具有相同对称性的B2Σ+和C2Σ+存在避免交叉,这也导致了它们的偶极矩极性反转.
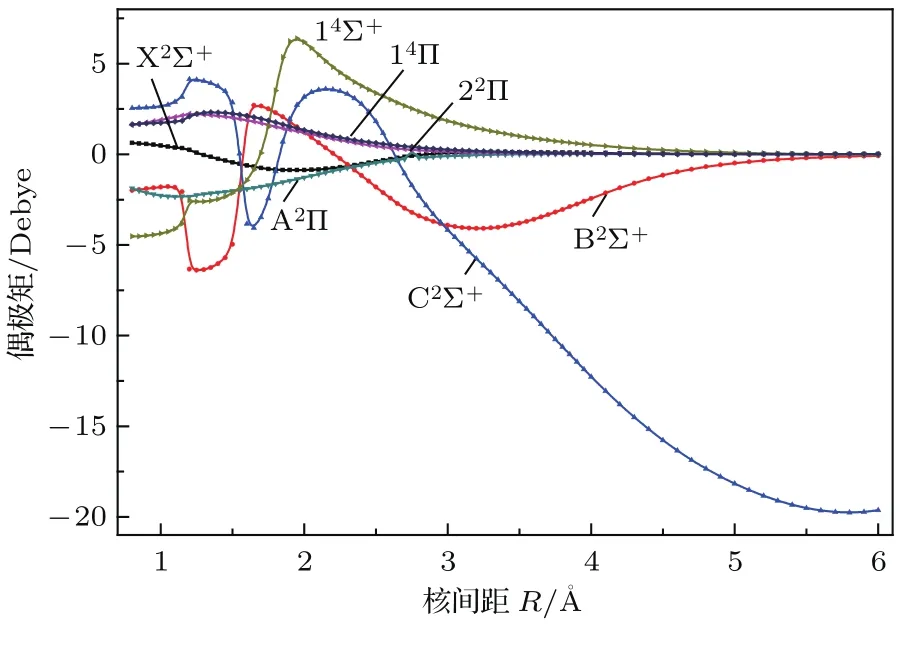
图3 (网刊彩色)Λ-S态的偶极矩曲线Fig.3.(color on line)D ipole m om ents cu rves of the Λ-S states.
3.2 Ω态势能曲线和光谱常数
考虑自旋-轨道耦合作用后,一个多重的Λ-S态会分裂成多个Ω态,Zn(3Pu)+H(2Sg)会劈裂为三条离解限Zn(3P0)+H(2S1/2),Zn(3P1)+H(2S1/2)和Zn(3P2)+H(2S1/2);其他三条离解限对应的是Zn和H的单态,不发生劈裂.Zn(3Pu)+H(2Sg)劈裂的三条离解限的激发能计算值分别为32605, 32495和32305 cm−1,与Zn原子的3P2,3P1和3P0的实验值[32]32890,32501和32311 cm−1接近,偏差分别为0.9%,0.02%和0.02%.
考虑自旋-轨道耦合后,原先的7个Λ-S态会劈裂成13个Ω态,其势能曲线绘于图4,其中包含8个Ω=1/2(图4(a)),4个Ω=3/2(图4(b))和1个Ω=5/2(图4(c)).能量较低的4个Ω束缚态的光谱常数见表2.在Franck-Condon区域,基态的组态成分几乎完全由X2Σ+构成,因此,它的光谱常数与Λ-S态的几乎相同.考虑自旋-轨道耦合后,第一激发态A2Π态会分裂成A2Π1/2和A2Π3/2,在平衡位置它们的能量劈裂值约为300 cm−1.A2Π1/2和A2Π3/2的离解能De分别为1.94和1.97 eV,比Λ-S态A2Π的值分别低约0.08和0.05 eV.从图1可以看出,第一激发态A2Π和第二激发态B2Σ+的势能曲线在R=2Å附近相交,由于它们都含有Ω=1/2的成分,因此,考虑自旋-轨道耦合后必然存在避免交叉.由于这两个态都被束缚在深势阱中,因此两者之间的相互作用不能够导致预解离的发生,但可能表现为光谱带上的扰动.第三激发态C2Σ+在R=1.85和2.3Å附近分别与两个排斥态14Σ+和14Π相交,在交叉点附近,束缚态与排斥态之间的自旋-轨道相互作用,可能会打开预解离通道.
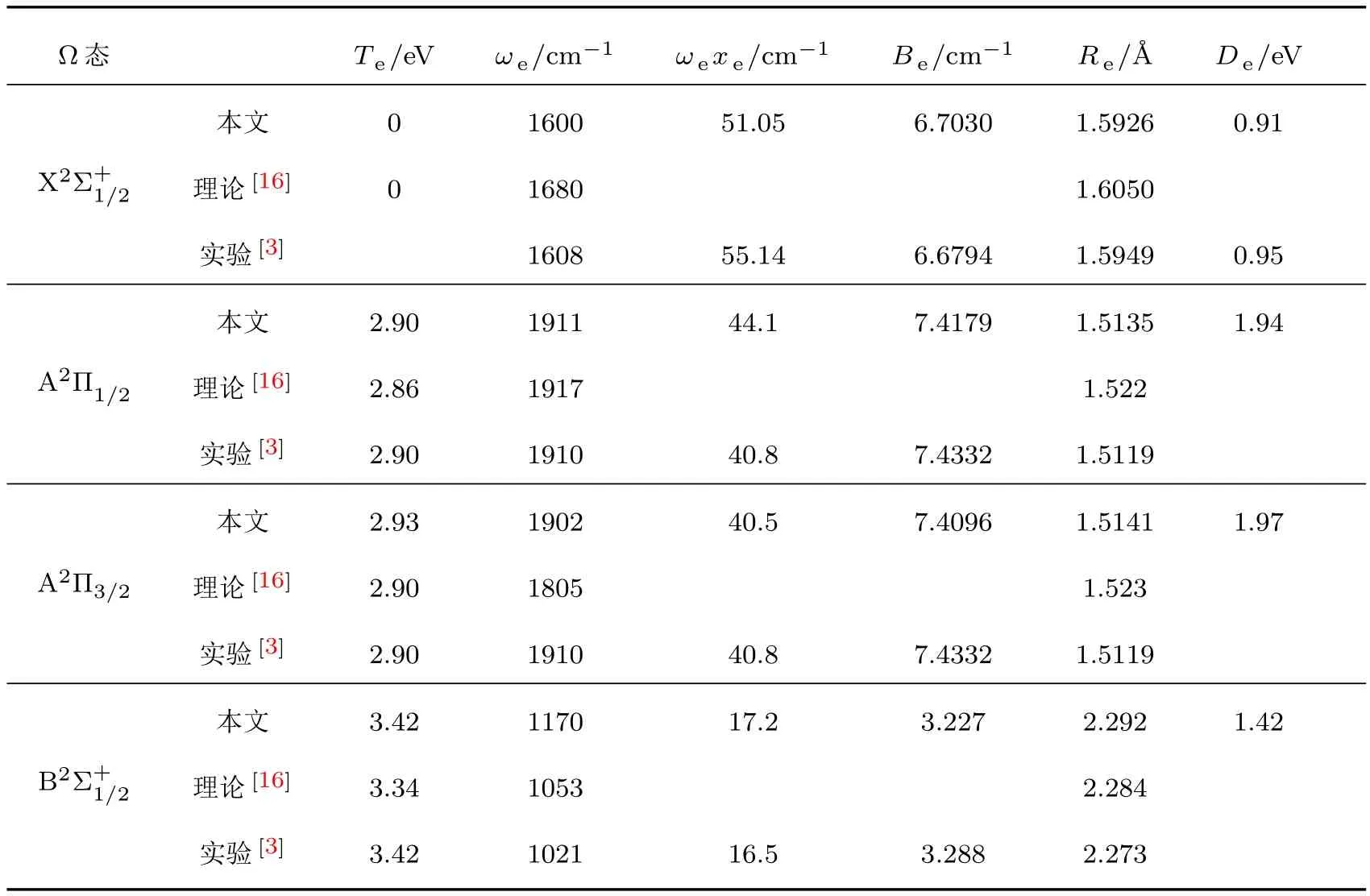
表2 ZnH分子较低Ω态的光谱常数Tab le 2.Spectroscop ic constants of the low-lyingΩstates of ZnH.
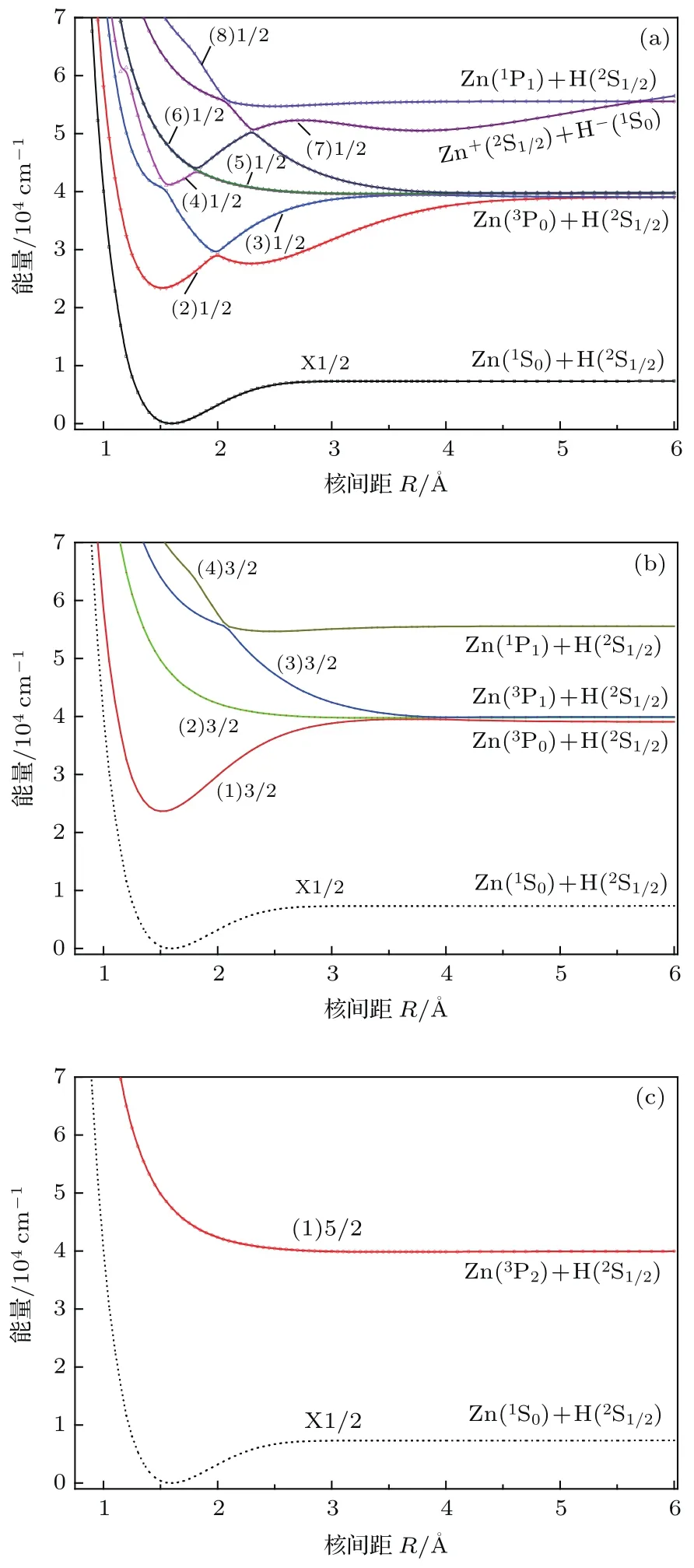
图4 (网刊彩色)Ω态的势能曲线 (a)Ω =1/2; (b)Ω=3/2;(c)Ω=5/2Fig.4.(color on line)Potential energy curves of theΩstates:(a)Ω=1/2;(b)Ω=3/2;(c)Ω=5/2.
由于具有相同对称性的Ω态会发生避免交叉现象,将会使势能曲线更加复杂,本文在特定的避免交叉区域R=1.75—2.05Å,给出了较低Ω态的主要Λ-S态组成百分比,见表3.从表3可以看出:在避免交叉点R=2Å附近,(2)1/2的主要Λ-S态组分从R=1.95Å时的12Π(99.2%)急剧变化为R=2.0Å时的22Σ+(95.3%),与之对应的是(3)1/2的主要组分从R=1.95Å时的22Σ+(99.2%)急剧变化为R=2.0Å时的12Π(95.3%);在避免交叉点R=1.85Å附近,(4)1/2的主要Λ-S态组分从R=1.8Å时的32Σ+(99.8%)急剧变化为R=1.85Å时的14Π(99.9%).上述对Ω态的波函数的细致分析,有助于进一步理解Ω态之间的跃迁性质.
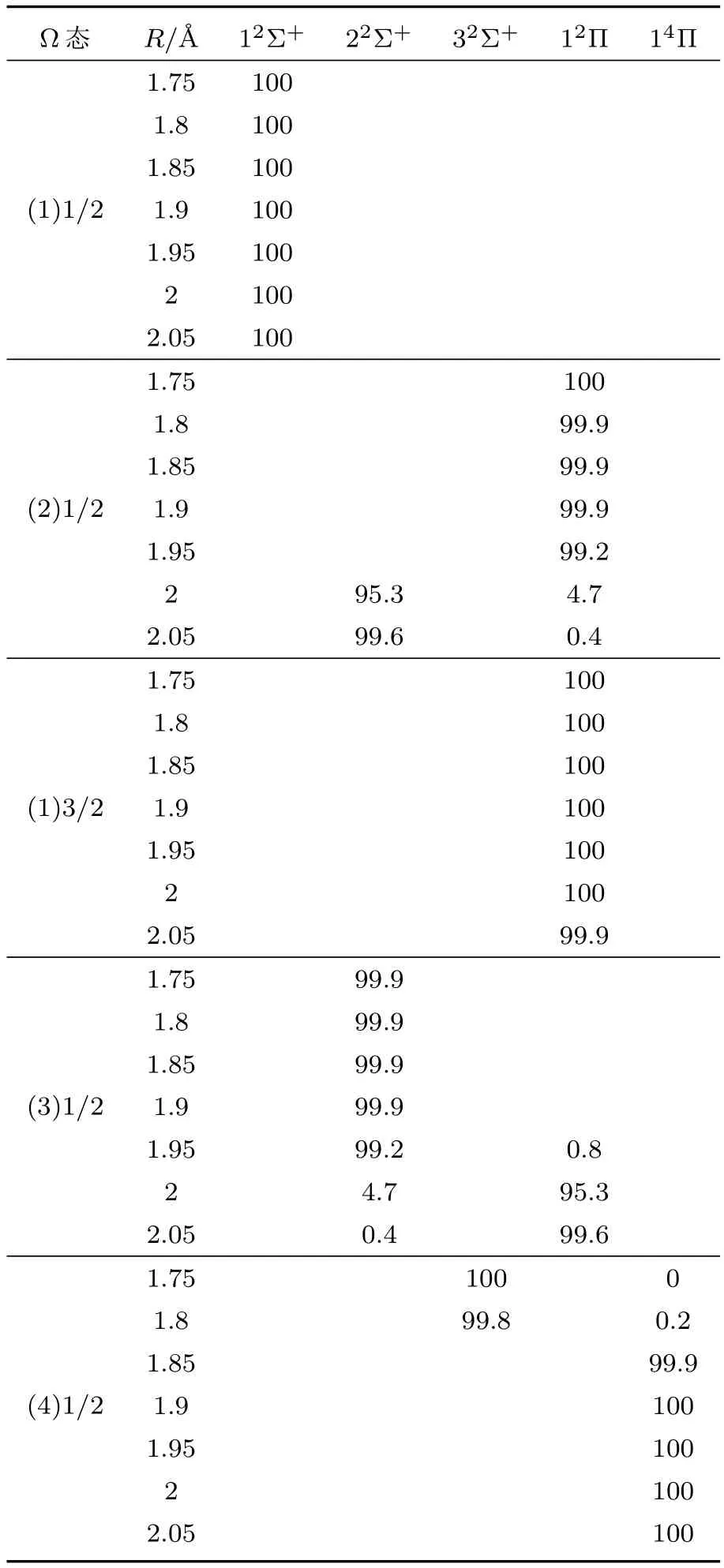
表3 ZnH分子较低Ω态在不同键长处的组态成分Tab le 3.Com position of the low-lyingΩstates of ZnH at som e selected bond lengths.
3.3 跃迁偶极矩和辐射寿命
图5给出了ZnH分子的激发态相对于基态的跃迁偶极矩(TDM)随核间距的变化.为了清晰地显示TDM的变化规律,Ω=1/2和Ω=3/2到基态的跃迁偶极矩分别在图5(a)和图5(b)显示.图5(a)中的(2)1/2—X 1/2和(3)1/2—X 1/2的跃迁主要来自于A2Π—X2Σ+和B2Σ+—X2Σ+的贡献,而(4)1/2—X 1/2,(6)1/2—X 1/2,(7)1/2—X1/2和(8)1/2—X1/2的跃迁主要来自于C2Σ+—X2Σ+,14Π—X2Σ+,22Π—X2Σ+和14Σ+—X2Σ+的贡献. 图5(b)中,(1)3/2—X 1/2的跃迁偶极矩主要源于由于A2Π3/2和没有相同的Ω分量,它们位于R=2.0Å附近的势能曲线交叉对(1)3/2—X 1/2的跃迁偶极矩没有影响,因此,它的跃迁偶极矩曲线未受到明显的组态混合的影响,无突变行为. (4)3/2—X1/2和(3)3/2—X 1/2跃迁主要分别来源于和跃迁. (3)3/2和(4)3/2态在R=2.0Å附近形成了一个避免交叉点,二者在该交叉点附近主要的Λ-S成分互换,因此(4)3/2—X 1/2和(3)3/2—X 1/2的跃迁偶极矩曲线在该交叉点存在突变. 应用数值方法求解Schrödinger方程,我们给出了(2)1/2—X 1/2,(3)1/2—X1/2,(4)1/2—X 1/2和(1)3/2—X1/2跃迁的Franck-Condon因子,相关结果列于表4.

图5 (网刊彩色)跃迁偶极矩曲线 (a)Ω=1/2—X 1/2;(b)Ω=3/2—X 1/2Fig.5.(color on line)Transition d ipole m om ents as a function of bond length:(a)Ω=1/2–X 1/2;(b)Ω= 3/2–X 1/2.

表4 说明(2)1/2—X 1/2,(3)1/2—X 1/2,(4)1/2—X 1/2和(1)3/2—X 1/2跃迁的Frank-Condon因子Tab le 4.Frank-Condon factors for(2)1/2–X 1/2,(3)1/2–X 1/2,(4)1/2–X 1/2 and(1)3/2–X 1/2.
基于束缚激发态和基态之间的Franck-Condon因子、TDM和振动能级之间的能量差值ΔE,应用(1)式,我们可以计算出束缚激发态某个振动能级的自发发射寿命τ:
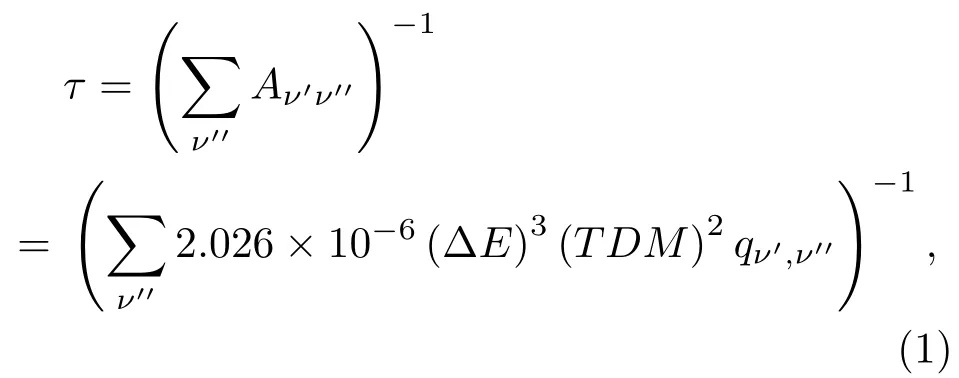
(1)式中能量差值ΔE的单位为cm−1;TDM的单位为a.u.;为振动态v′和v′′振动波函数的重叠积分,即Franck-Condon因子;τ的单位为s.应用(1)式,我们计算得到了辐射跃迁(2)1/2—X1/2, (3)1/2—X1/2,(4)1/2—X 1/2和(1)3/2—X 1/2的最低三个振动能级的自发发射寿命,并列于表5中.由表5可知,(2)1/2态的v′=0振动能级的辐射寿命为60.3 ns,介于实验值47—77 ns之间[33−35].与(2)1/2态的情况类似,在(1)3/2态中,v′=0振动能级的辐射寿命为59 ns,也介于实验值47—73 ns之间[33−35].另外两个态(3)1/2和(4)1/2的辐射寿命都在百纳秒量级.
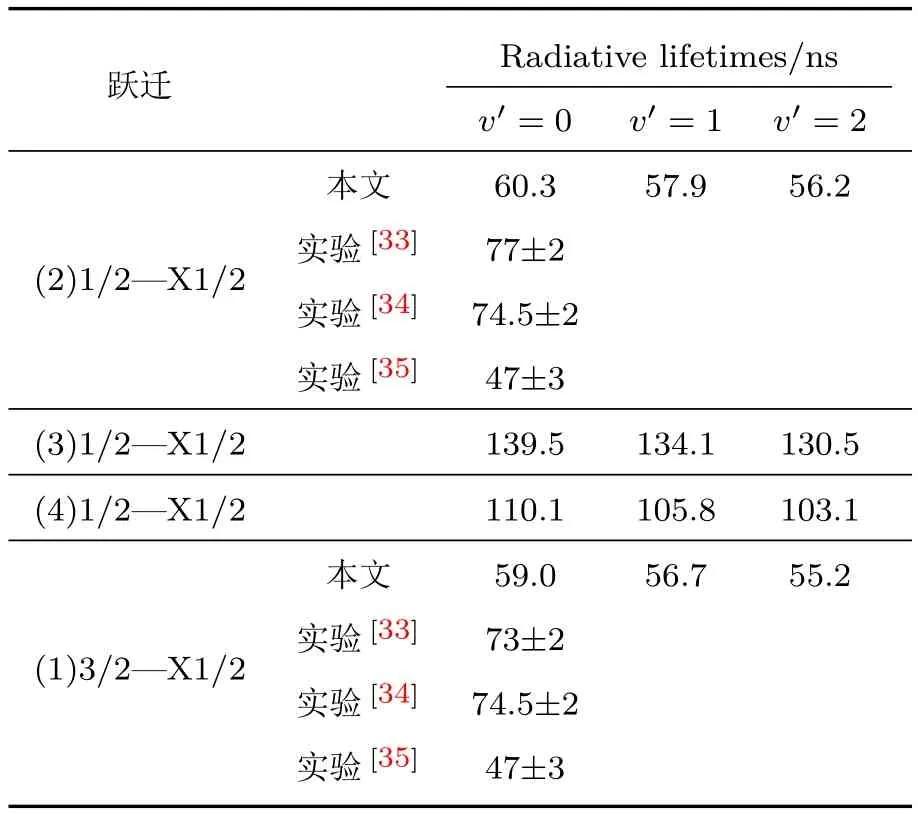
表5 说明(2)1/2,(3)1/2,(4)1/2和(1)3/2到X 1/2跃迁的辐射寿命Tab le 5.Radiative lifetim es of(2)1/2,(3)1/2,(4)1/2 and(1)3/2 to ground X 1/2 state.
4 结 论
本论文应用高精度的MRCI方法和全电子基组计算了ZnH分子的能量较低的7个Λ-S态的电子结构.计算中还考虑了Davidson修正和Zn的 3s23p63d10电子的关联效应;通过计算Douglas-K roll-Hess积分给出标量相对论效应对电子结构的影响;进一步地,借助避免交叉规则,我们得到了该分子的7个Λ-S态的势能曲线.为了提高计算结果的精确性,通过计算全电子Breit-Pauli算符,纳入了自旋-轨道耦合效应对电子态结构的影响,给出了该分子13个Ω态的势能曲线.基于计算的Λ-S态和Ω态的势能曲线,应用数值积分方法拟合出了束缚态的光谱常数,计算的束缚态的光谱常数与之前的实验和理论结果符合较好.本文的计算结果表明C2Σ+态为一个离子对态.分析了ZnH分子Λ-S态和Ω态避免交叉点附近的电子波函数的成分变化,并详细讨论了避免交叉现象对跃迁偶极矩的影响.基于计算的光谱常数信息,得到了束缚激发态v′=0—2振动能级的自发发射寿命.
[1]Li Y,X i G 2005 J.Hazard.M ater.127 244
[2]Peruzzini M,Poli R 2001 Recen t Advances in Hydride Chem istry(Am sterdam:E lsevier)pp89–90
[3]Huber K P,Herzberg G 1979 M olecu lar Spectra and M olecu lar Structure IV:Constan ts of D iatom ic M olecu les(New York:Van Nostrand Reinhold) pp678–679
[4]Hayashi S,Léonard C,Chambaud G 2009 J.Phys. Chem.A 113 14615
[5]Bucchino M P,Ziurys L M 2013 J.Phys.Chem.A 117 9732
[6]W atson W W 1930 Phys.Rev.36 1134
[7]Fu jioka Y,Tanaka Y 1937 Sci.Pap.Inst.Phys.Chem. Res.Jpn.32 143
[8]M rozow ski S 1940 Phys.Rev.58 597
[9]K han M A 1962 Proc.Phys.Soc.80 599
[10]U rban R,M agg U,Birk H,Jones H 1990 J.Chem.Phys. 92 14
[11]Shayesteh A,Le Roy R J,Varberg T D,Bernath P F 2006 J.M ol.Spectrosc.237 87
[12]Ishiguro E,Kobori M 1967 J.Phys.Soc.Jpn.22 263
[13]Veseth L 1971 J.M ol.Spectrosc.38 228
[14]Chong D P,Langhoff S R,Bausch licher C W,W alch S P,Partridge H 1986 J.Chem.Phys.85 2850
[15]Chong D P,Langhoff SR 1986 J.Chem.Phys.84 5606
[16]Jam orski C,Dargelos A,Teichteil C,Daudey J P 1994 J.Chem.Phys.100 917
[17]K erkines ISK,M av ridis A,K aripid is P A 2006 J.Phys. Chem.A 110 10899
[18]W ang L,Liu Y R,Cao Y,Huang C J,Chen X H 2010 J.A t.M ol.Phys.27 673(in Chinese)[王玲,刘议蓉,曹勇,黄昌军,谌晓洪2010原子与分子物理学报27 673]
[19]Yuan L,Fan Q C,Sun W G,Fan Z X,Feng H 2014 Acta Phys.Sin.63 043102(in Chinese)[袁丽,樊群超,孙卫国,范志祥,冯灏2014物理学报63 043102]
[20]W ang W B,Yu K,Zhang X M,Liu Y F 2014 Acta Phys. Sin.63 073302(in Chinese)[王文宝,于坤,张晓美,刘玉芳2014物理学报63 073302]
[21]Liang G Y 2016 M.S.D issertation(Changchun:Jilin University)(in Chinese)[梁桂颖2016硕士学位论文(长春:吉林大学)]
[22]W erner H J,Know les P J,Knizia G,et al.2010 MOLPRO,a Package ofab initio Program s(version 2010.1)
[23]Balabanov N B,Peterson K A 2005 J.Chem.Phys.123 64107
[24]Know les P J,Werner H J 1985 Chem.Phys.Lett.115 259
[25]W erner H J,Know les P J 1985 J.Chem.Phys.82 5053
[26]Know les P J,Werner H J 1988 Chem.Phys.Lett.145 514
[27]W erner H J,Know les P J 1988 J.Chem.Phys.89 5803
[28]Berning A,Schweizer M,W erner H J,Know les P J, Palm ieri P 2000 M ol.Phys.98 1823
[29]W inter N W,Pitzer R M 1988 J.Chem.Phys.89 446
[30]T ilson J L,Erm ler W C 2014 Theor.Chem.Acc.133 1564
[31]Le Roy R J 2007 LEVEL 8.0:a Com puter Program for So lving the Radial Schröinger Equation for Bound and Quasibound Levels(Waterloo:University of Waterloo) Chem ical Physics Research Report CP-663
[32]M oore C E 1971 Atom ic Energy Level s(Washington, DC:National Bu reau of Standards Pub lications)
[33]KedzierskiW,Supronow icz J,Atkinson J B,K rause L 1990 Can.J.Phys.68 526
[34]Nedelec O,Dufayard J 1984 Chem.Phys.84 167
[35]Du fayard J,Nedelec O 1977 J.Phys.France 38 449
PACS:31.50.D f,31.15.aj,31.15.agDOI:10.7498/aps.66.063103
Theoretical study on the electron ic structu re and transition p roperties of excited state of ZnH m olecu le∗
Zhao Shu-Tao1)2)†Liang Gui-Ying2)Li Rui3)LiQi-Nan3)Zhang Zhi-Guo1)Yan Bing2)‡
1)(School of Physics and Electronic Science,Fuyang Norm al College,Fuyang 236037,China)
2)(Jilin Provincial Key Laboratory of App lied A tom ic and M olecu lar Spectroscopy(Jilin University),Institu te of A tom ic and
M olecu lar Physics,Jilin University,Changchun 130012,China)
3)(Departm ent of Physics,College of Science,Q iqihar University,Qiqihar 161006,China)
(Received 7 Decem ber 2016;revised m anuscrip t received 23 January 2017)
The potential energy curves(PECs)associated w ith the lowest four dissociation lim its,i.e.,Zn(1Sg)+H(2Sg), Zn(3Pu)+H(2Sg),Zn+(2Sg)+H−(1Sg)and Zn(1Pu)+H(2Sg),are calculated by using a high-levelconfiguration interaction m ethod.The Davidson correction,scalar relativistic eff ect and spin-orbit coup ling eff ect are taken into account in calculation.On thebasisofour calculated PECsofΛ-SandΩstates,the spectroscopic constants including Te,ωe,ωeχe,Beand Reare evaluated by num erical solution of one-dim ensional Schrödinger equation.The com puted spectroscopic constants are reasonably consistent w ith previous experim ental results.The dipolem om ent curves of the 7Λ-S states are presented,and the infl uences of the variation of electronic configuration on the dipolemoment and bonding property are discussed.The com putational results reveal the ionic character of the C2Σ+state.The variation ofΛ-S com ponent forΩstate near the avoided crossing point is illum inated,which is used to exp lain the change of transition dipolem om ent (TDM)around the avoided crossing point.Based on the TDM s,Franck-Condon factors and the transition energies,the radiative lifetim es of v′=0–2 vibrational levels of(2)1/2,(3)1/2,(4)1/2 and(1)3/2 states are p redicted,which accord wellw ith the available experimental values.
ZnH,multi-reference configuration interaction method,spectroscopic constant,radiative lifetime
10.7498/aps.66.063103
∗国家自然科学基金(批准号:11604052,11404180,11574114)、安徽省自然基金(批准号:1608085QA 19)、黑龙江省自然基金(批准号:A 2015010)、黑龙江省普通本科高等学校青年创新人才培养计划(批准号:2015095)和吉林省自然基金(批准号: 20150101003JC)资助的课题.
†通信作者.E-m ail:zhaoshu tao2002@163.com
‡通信作者.E-m ail:yanbing@jlu.edu.cn
*Pro ject supported by the National Natu ral Science Foundation of China(G rant Nos.11604052,11404180,11574114), the Natu ral Science Foundation of Anhui Province,China(G rant No.1608085QA 19),the Natu ral Science Foundation of Heilongjiang Province,China(G rant No.A 2015010),the University Nu rsing Program for Young Scholars w ith Creative Talents in Heilong jiang Province,China(G rant No.2015095),and the Natural Science Foundation of Jilin Province,China (G rant No.20150101003JC).
†Corresponding author.E-m ail:zhaoshutao2002@163.com
‡Corresponding au thor.E-m ail:yanbing@jlu.edu.cn
