数学中的分类讨论思想

吕美英

数学中的分类讨论思想

吕美英

（重庆师范大学 数学科学学院，重庆 401331）

在数学问题的众多研究方法中，分类讨论是一种最常见的研究方法.当我们遇到的数学问题比较复杂，不能统一用一种方法解决时，我们一般会根据条件的不同分类去讨论，最后再将结论整合到一起，本文主要从实际问题出发来探讨该方法的重要性.

数学；分类讨论；方法

每个数学结论都有其成立的条件，每一种数学方法的使用也往往有其适用范围，在我们所遇到的数学问题中，有些问题的结论不是唯一确定的，有些问题的结论在解题中不能以统一的形式进行研究，还有些问题的已知量是用字母表示数的形式给出的，这样字母的取值不同也会影响问题的解决，由上述几类问题可知，就其解题方法及转化手段而言都是一致的，即把所有研究的问题根据题目的特点和要求，分成若干类，转化成若干个小问题来解决，这种按不同情况分类，然后再逐一研究解决的数学思想，称之为分类讨论思想.

分类讨论思想的应用要把握以下三个原则：一、每一级的分类应该按同一标准进行，这就需要明确引起分类讨论的原因，根据原因确定分类讨论的标准；二、分类应逐级进行，而且每一级分类要有统一的标准，否则容易造成分类不清，影响结论的正确性；三、同级互斥，不得越级，这样才能保证分类的对象不重复，不遗漏.

下面我们从数学的实际问题出发，来探讨分类讨论思想的应用：

1 高等代数中的分类讨论

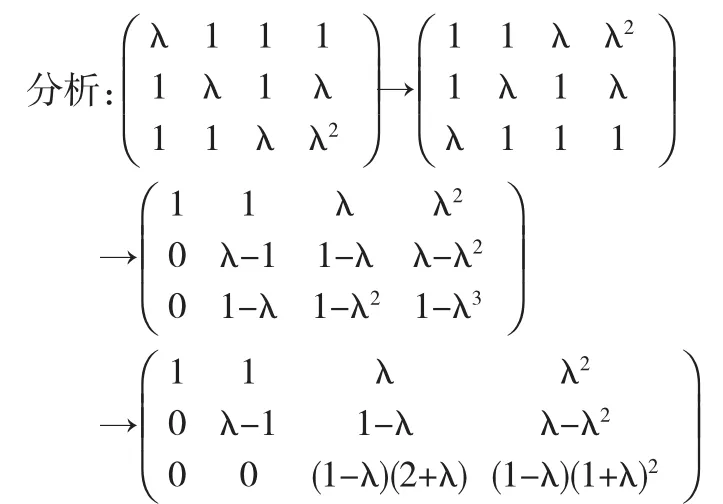
所以，当λ≠1且≠-2时，方程组有唯一解；当λ=-2时，方程组无解；当λ=1时，方程组有无穷多个解.

2 数学分析中的分类讨论

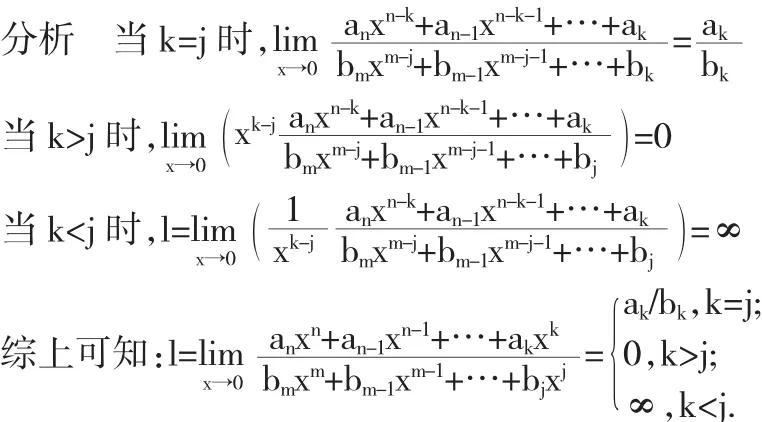
3 概率论中的分类讨论

例3 盒子中装有编号为1,2,3,4,5,6,7,8,9的九个球，从中任意取出两个，求这两个球的编号之积为偶数的概率.

解析 从1,2,3,4,5,6,7,8,9九个球中，任意取出两个球的取法种数为C92=36种，取出两个球的编号之积为偶数有两种情况：一奇一偶；两个偶数.

一奇一偶有C51·C41=20种，两个偶数有C42=6种，故两个球的编号之积为偶数的情况有20+6=26种，所以取出两个球的编号之积为偶数的概率为

以上只是作者对分类讨论方法的简单分析，实际问题中还有很多类似的例子.分类讨论的思想不光适用于高等代数，数学分析等课程，它适用于数学的任何学科，而且是解决数学问题的一种重要的手段和方法.分类讨论解决问题首先要明确分类的对象，分类的标准，然后逐级分类，分级得到阶段性的结果，并用该级标准进行检验筛选结果，最后归纳给出结论.该思想不仅可以培养学生分析问题，解决问题的能力，同时还可以提高学生数学思维的严谨性，缜密性和灵活性.

〔1〕陈纪修，於崇华，金路.数学分析(第二版)[M].北京：高等教育出版社.2004.

〔2〕吴传生.经济数学—线性代数(第二版)[M].北京：高等教育出版社，2009.

〔3〕王艳青，代钦.高中数学解题教学中的分类讨论策略[J].内蒙古师范大学学报(教育科学版),2011，24(12)：121-122.

G420

A

1673-260X（2017）07-0007-01

2017-03-23

重庆师范大学基金项目：Cantor集上丢番图逼近与Beta-连分数的若干研究（12XLZ02）